【学习笔记】lyndon分解
摘抄自quack的ppt。
这部分和 s a sa sa的关联比较大,可以加深对 s a sa sa的理解。
Part 1
如果字符串 s s s的字典序在 s s s以及 s s s的所有后缀中是最小的,则称 s s s是一个 lyndon \text{lyndon} lyndon串。
lyndon \text{lyndon} lyndon分解,指的是把一个字符串分成若干段,每一段都是一个 lyndon \text{lyndon} lyndon串,问最少的分割段数。
方法一:用后缀数组, s a [ 1 ] sa[1] sa[1]就是 lyndon \text{lyndon} lyndon分解的最后那一段, lyndon \text{lyndon} lyndon分解倒数第二段就是把 s a [ 1 ] sa[1] sa[1]那一段排除之后排的最靠前的 s a sa sa,以此类推。
s a sa sa可以用来 lyndon \text{lyndon} lyndon分解依赖于以下结论:
定义数组 a [ i ] a[i] a[i]为最小的 j j j,使得 j > i j>i j>i且 S [ j : ∣ S ∣ − 1 ] < S [ i : ∣ S ∣ − 1 ] S[j:|S|-1]<S[i:|S|-1] S[j:∣S∣−1]<S[i:∣S∣−1],如果不存在这样的 j j j,可以认为 a i = ∣ S ∣ a_i=|S| ai=∣S∣。
那么, S S S的 lyndon \text{lyndon} lyndon分解的第一项为 S [ 0 : a [ 0 ] − 1 ] S[0:a[0]-1] S[0:a[0]−1],且后面 m − 1 m-1 m−1项就是 S [ a [ 0 ] : ∣ S ∣ − 1 ] S[a[0]:|S|-1] S[a[0]:∣S∣−1]的 lyndon \text{lyndon} lyndon分解。
证明:显然此时不能划分到 a [ 0 ] a[0] a[0]之后,否则可以根据原串后缀的信息道出矛盾。因此只需论证划分到 a [ 0 ] a[0] a[0]合法即可。注意到此时 S [ a [ 0 ] ] ≤ S [ 0 ] S[a[0]]\le S[0] S[a[0]]≤S[0],因此对于任意 j ∈ [ 1 , a [ 0 ] − 1 ] j\in [1,a[0]-1] j∈[1,a[0]−1],一定满足 S [ 0 : a [ 0 ] − j − 1 ] ≠ S [ j : a [ 0 ] − 1 ] S[0:a[0]-j-1]\ne S[j:a[0]-1] S[0:a[0]−j−1]=S[j:a[0]−1],又因为 s a [ 0 ] < s a [ j ] sa[0]<sa[j] sa[0]<sa[j],因此 S [ 0 : a [ 0 ] − 1 ] S[0:a[0]-1] S[0:a[0]−1]一定是它的所有后缀当中最小的。
基本性质:
1.1 1.1 1.1 若字符串 u , v u,v u,v是 lyndon \text{lyndon} lyndon串且 u < v u<v u<v,则 u v uv uv是 lyndon \text{lyndon} lyndon串。
1.2 1.2 1.2 若字符串 s s s是 lyndon \text{lyndon} lyndon串, s ′ a s'a s′a是 s s s的前缀,那么 s ′ b ( b > a ) s'b(b>a) s′b(b>a)是 lyndon \text{lyndon} lyndon串。(注意 s ′ a s'a s′a不一定是 lyndon \text{lyndon} lyndon串)
方法二:duval 算法
每次维护一个前缀的 lyndon \text{lyndon} lyndon分解。这个前缀 S [ 1 : k − 1 ] S[1:k-1] S[1:k−1]可以被分解成 s 1 , . . . , s g s_1,...,s_g s1,...,sg这些 lyndon \text{lyndon} lyndon串和 S [ i : k − 1 ] S[i:k-1] S[i:k−1]这个近似 lyndon \text{lyndon} lyndon串(形如 w k w ′ w^kw' wkw′, w w w是一个 lyndon \text{lyndon} lyndon串, w ′ w' w′是 w w w的前缀)。
具体的,三个变量 i , j , k i,j,k i,j,k维持一个循环不变式:
- S [ 0 : i − 1 ] = s 1 s 2 . . . s g S[0:i-1]=s_1s_2...s_g S[0:i−1]=s1s2...sg 是已经固定下来的分解,满足 s l s_l sl是 lyndon \text{lyndon} lyndon串,且 s l ≥ s l + 1 s_l\ge s_{l+1} sl≥sl+1(否则可以合并)。
- S [ i : k − 1 ] = t 1 t 2 . . . t h v S[i:k-1]=t_1t_2...t_hv S[i:k−1]=t1t2...thv是没有固定的分解,满足 t 1 t_1 t1是 lyndon \text{lyndon} lyndon串, t 1 = t 2 = . . . = t h t_1=t_2=...=t_h t1=t2=...=th, v v v是 t h t_h th的(可为空的)真前缀,令 j = k − ∣ t 1 ∣ j=k-|t_1| j=k−∣t1∣。

复杂度为 O ( n ) O(n) O(n)。比sa快啊
代码
Part 2
lyndon \text{lyndon} lyndon分解的应用:
1.3 1.3 1.3 给定长为 n n n的字符串 S S S,求出 S S S的最小表示法。
方法:将 S S SS SS lyndon \text{lyndon} lyndon分解,找到分解后最后一个字符串,它的首字符为 S S [ p ] SS[p] SS[p],且 p ∈ [ 0 , ∣ S ∣ ) p\in [0,|S|) p∈[0,∣S∣)。可以证明 S S [ p : p + ∣ S ∣ − 1 ] SS[p:p+|S|-1] SS[p:p+∣S∣−1]是字典序最小的。(运用第一条引理,转化为比较在原串中的后缀,即sa)
1.4 1.4 1.4 给定长度为 n n n的字符串 S S S,将 S S S分为最多 k k k个串 c 1 c 2 . . . c k c_1c_2...c_k c1c2...ck,求 max c i \max c_i maxci的最小值。
方法:看到字典序,容易想到 lyndon \text{lyndon} lyndon分解。首先把 S S S lyndon \text{lyndon} lyndon分解成 s 1 , . . . , s g s_1,...,s_g s1,...,sg,如果 k ≥ g k\ge g k≥g,那么答案即为 s 1 s_1 s1;否则,如果 s 1 > s 2 s_1>s_2 s1>s2,那么显然可以分成 s 1 s_1 s1和剩下的所有串,答案还是 s 1 s_1 s1。因此,考虑分解成 s 1 m s g s_1^ms_g s1msg的情况,如果 k > m k>m k>m,那么答案还是 s 1 s_1 s1,如果 k ≤ m k\le m k≤m,那么尽量均分一下即可。
推广:多次询问,每次询问 S S S的一段后缀的答案。
考虑求出原串的sa数组,显然可以求出第一项以及重复次数(可以用哈希),这样就做完了。
1.5 1.5 1.5 求 S S S的每个前缀的字典序最小的后缀
首先把 S S S lyndon \text{lyndon} lyndon分解成 s 1 , . . . , s g s_1,...,s_g s1,...,sg,显然 s 1 . . . s k s_1...s_k s1...sk的字典序最小的后缀是 s k s_k sk。但是前缀取到分解出来的 lyndon \text{lyndon} lyndon串半截时,答案可能不一样。
考虑 duval \text{duval} duval算法求 lyndon \text{lyndon} lyndon分解的过程,分类讨论:
- 若 s [ k ] > s [ j ] s[k]>s[j] s[k]>s[j],此时 a n s [ k ] ans[k] ans[k]应该等于 i i i,因为 s [ i : k ] s[i:k] s[i:k]构成一个新的 lyndon \text{lyndon} lyndon串
- 若 s [ k ] = s [ j ] s[k]=s[j] s[k]=s[j],此时 a n s [ k ] = a n s [ j ] + k − j ans[k]=ans[j]+k-j ans[k]=ans[j]+k−j
- 若 s [ k ] < s [ j ] s[k]<s[j] s[k]<s[j],在 lyndon \text{lyndon} lyndon串开头时更新
1.6 1.6 1.6 求 S S S的每个前缀的字典序最大的后缀
首先把字符比较反过来,然后要尽量向左取,当 s [ k ] ≤ s [ j ] s[k]\le s[j] s[k]≤s[j]的时候, s [ i : k ] s[i:k] s[i:k]这一段都保持了是一个近似 lyndon \text{lyndon} lyndon串,所以都取近似 lyndon \text{lyndon} lyndon串的左端点 i i i作为答案即可。
ps:感觉这个算法就只能考论文题。。。太恶心了。。。
相关文章:

【学习笔记】lyndon分解
摘抄自quack的ppt。 这部分和 s a sa sa的关联比较大,可以加深对 s a sa sa的理解。 Part 1 如果字符串 s s s的字典序在 s s s以及 s s s的所有后缀中是最小的,则称 s s s是一个 lyndon \text{lyndon} lyndon串。 lyndon \text{lyndon} lyndon分解&a…...

21、命令执行
文章目录 一、命令执行概述1.1 基本定义1.2 原理1.3 两个条件1.4 命令执行漏洞产生的原因1.5 管道符号和通用命令符 二、远程命令执行2.1 远程命令执行相关函数2.2 远程命令执行漏洞的利用 三、系统命令执行3.1 相关函数3.2 系统命令执行漏洞利用 四、命令执行漏洞防御 一、命令…...
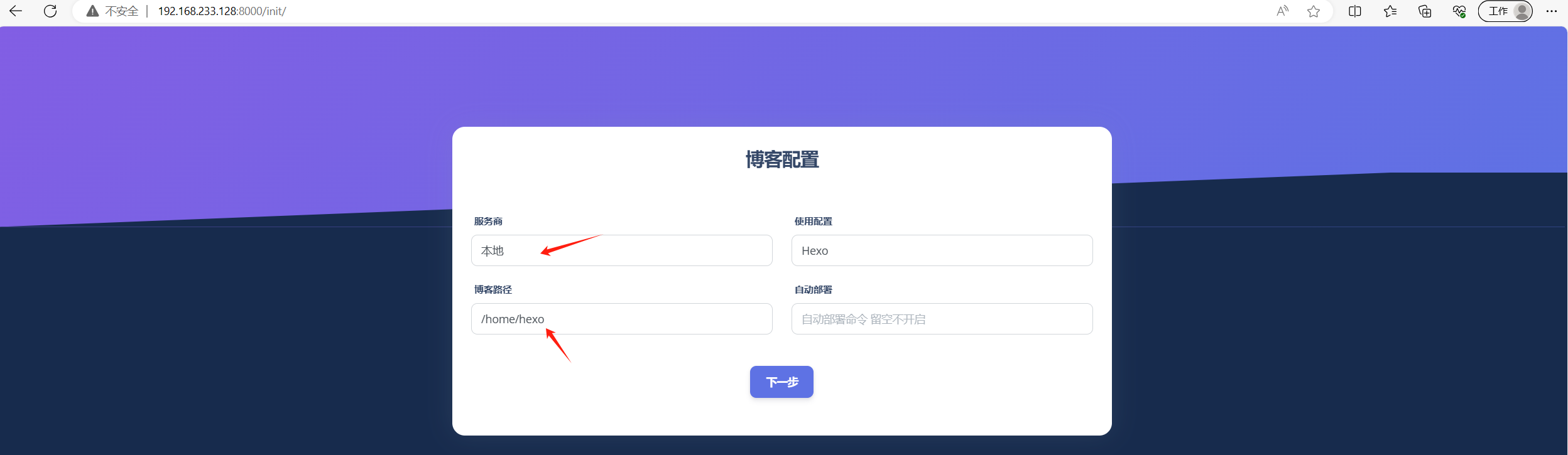
Qexo博客后台管理部署
Qexo博客后台管理部署 个人主页 个人博客 参考文档 https://www.oplog.cn/qexo/本地部署 采用本地Docker部署管理本地Hexo 下载代码包 若无法下载使用科学工具下载到本地在上传到服务器 wget https://github.com/Qexo/Qexo/archive/refs/tags/3.0.1.zip# 解压 unzip Qexo…...

最小生成树prim
最小生成树(三)Prim算法及存储结构_哔哩哔哩_bilibili 311 最小生成树 Prim 算法_哔哩哔哩_bilibili #include <iostream> #include <queue> #include <string> #include <stack> #include <vector> #include <set…...
实用篇 | 一文学会人工智能中API的Flask编写(内含模板)
----------------------- 🎈API 相关直达 🎈-------------------------- 🚀Gradio: 实用篇 | 关于Gradio快速构建人工智能模型实现界面,你想知道的都在这里-CSDN博客 🚀Streamlit :实用篇 | 一文快速构建人工智能前端展…...
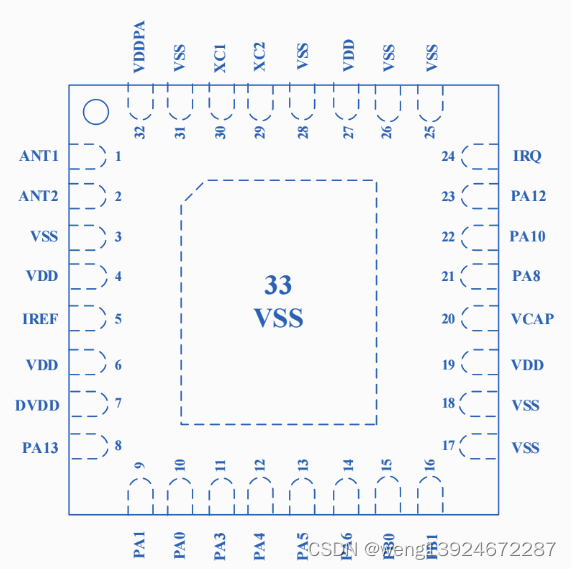
Si24R03—低功耗 SOC 芯片(集成RISC-V内核+2.4GHz无线收发器)
Si24R03是一款高度集成的低功耗SOC芯片,其集成了基于RISC-V核的低功耗MCU和工作在2.4GHz ISM频段的无线收发器模块。 MCU模块具有低功耗、Low Pin Count、宽电压工作范围,集成了13/14/15/16位精度的ADC、LVD、UART、SPI、I2C、TIMER、WUP、IWDG、RTC等丰…...

C# Winform 日志系统
目录 一、效果 1.刷新日志效果 2.单独日志的分类 3.保存日志的样式 二、概述 三、日志系统API 1.字段 Debug.IsScrolling Debug.Version Debug.LogMaxLen Debug.LogTitle Debug.IsConsoleShowLog 2.方法 Debug.Log(string) Debug.Log(string, params object[]) …...

【Java 基础】27 XML 解析
文章目录 1.SAX 解析器1)什么是 SAX2)SAX 工作流程初始化实现事件处理类解析 3)示例代码 2.DOM 解析器1)什么是 DOM2)DOM 工作流程初始化解析 XML 文档操作 DOM 树 3)示例代码 总结 在项目开发中࿰…...

地图服务 ArcGIS API for JavaScript基础用法全解析
地图服务 ArcGIS API for JavaScript基础用法全解析 前言 在接触ArcGIS之前,开发web在线地图时用过Leaflet来构建地图应用,作为一个轻量级的开源js库,在我使用下来Leaflet还有易懂易用的API文档,是个很不错的选择。在接触使用Ar…...
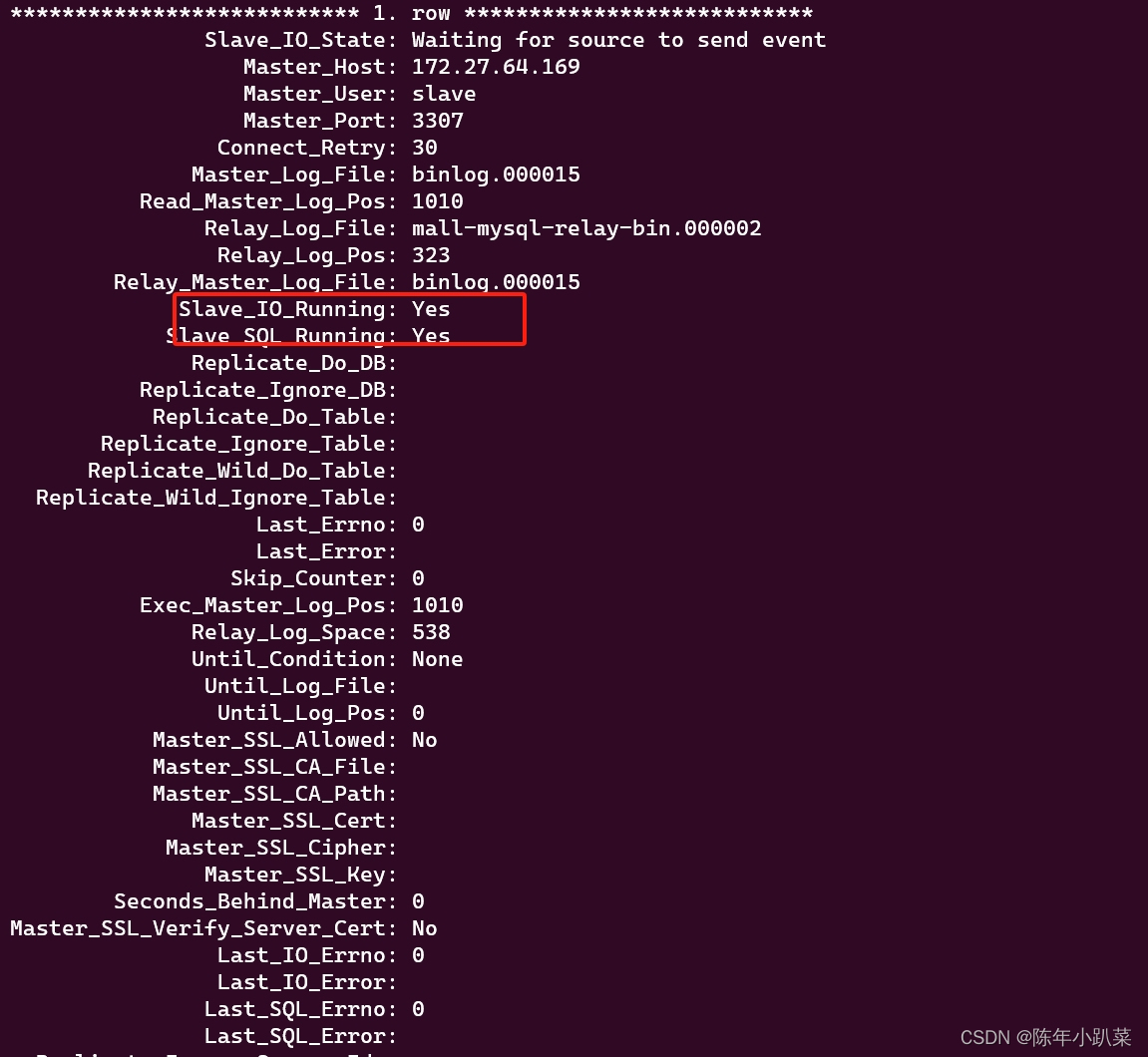
docker学习(八、mysql8.2主从复制遇到的问题)
在我配置主从复制的时候,遇到了一直connecting的问题。 起初可能是我ip配置的不对,slave_io_running一直connecting。(我的环境:windows中安装了wsl,是ubuntu环境的,在wsl中装了miniconda,mini…...
:表单验证)
React-hook-form-mui(三):表单验证
前言 在上一篇文章中,我们介绍了react-hook-form-mui的基础用法。本文将着重讲解表单验证功能。 react-hook-form-mui提供了丰富的表单验证功能,可以通过validation属性来设置表单验证规则。本文将详细介绍validation的三种实现方法,以及如何…...

【私域运营秘籍】4大用户调研方法,让你轻松掌握用户心理!
我们常说私域运营的核心是用户运营。根据二八法则,20%的超级用户贡献企业80%的利润。因此,企业应该根据用户的价值贡献来有针对性地进行运营。 然而,在实际的私域运营中,我们不仅需要找出贡献价值不同的用户,还可以从…...

2.8寸 ILI9341 TFTLCD 学习移植到STM32F103C8T6
2.8寸 ILI9341 TFTLCD 学习移植到STM32F103C8T6 文章目录 2.8寸 ILI9341 TFTLCD 学习移植到STM32F103C8T6前言第1章 LCD简介1.1 LCD硬件接口介绍 第2章 LCD指令介绍第3章 LCD 8080驱动方式3.1 8080写时序3.2 8080读时序 第4章 LCD 驱动代码部分4.1 修改代码部分4.2 代码工程下载…...

Java利用TCP实现简单的双人聊天
一、创建新项目 首先创建一个新的项目,并命名为聊天。然后创建包,创建两个类,客户端(SocketClient)和服务器端(SocketServer) 二、实现代码 客户端代码: package 聊天; import ja…...

软件压力测试的重要性与用途
在当今数字化的时代,软件已经成为几乎所有行业不可或缺的一部分。随着软件应用规模的增加和用户数量的上升,软件的性能变得尤为关键。为了确保软件在面对高并发和大负载时仍然能够保持稳定性和可靠性,软件压力测试变得至关重要。下面是软件压…...

【数据挖掘】国科大苏桂平老师数据库新技术课程作业 —— 第二次作业
1 设 F { A B → C , B → D , C D → E , C E → G H , G → A } F\{AB\rightarrow C,B\rightarrow D, CD\rightarrow E, CE\rightarrow GH, G\rightarrow A \} F{AB→C,B→D,CD→E,CE→GH,G→A},用推理的方法证明 F ∣ A B → G F\;|AB\rightarrow G F∣AB→…...
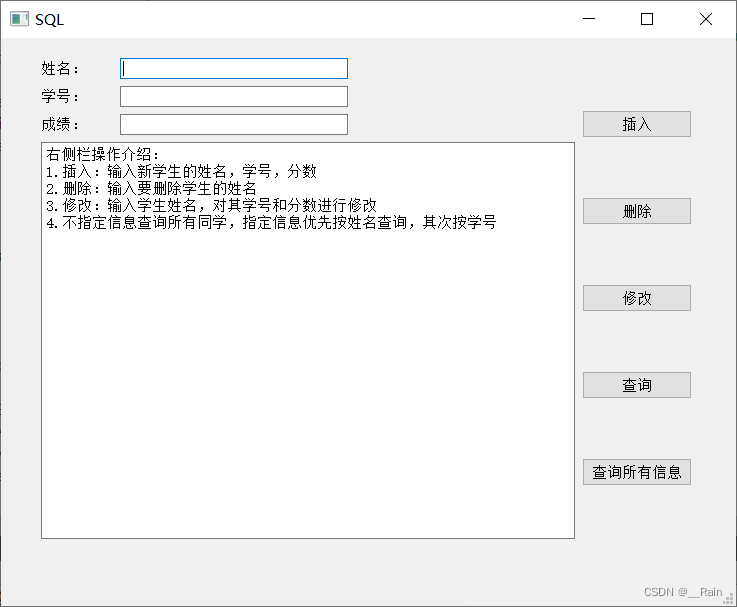
Qt + MySQL(简单的增删改查)
Qt编译MySql插件教程 帮助: SQL Programming QSqlDatabase 静态函数 1.drivers(),得到可以使用的数据库驱动名字的集合 [static] QStringList QSqlDatabase::drivers();2.addDatabase(),添加一个数据库实例 [static] QSqlDatabase QSql…...

postgresql设置免密登录
您提供的步骤描述了在 PostgreSQL 数据库环境中配置服务器间的 SSH 无密码登录和数据库用户认证的过程。这些步骤主要用于设置一个高可用性、负载平衡的数据库集群环境。让我们逐一解释这些步骤的目的和应用场景: 1. 启动 PostgreSQL 服务 systemctl start postgr…...
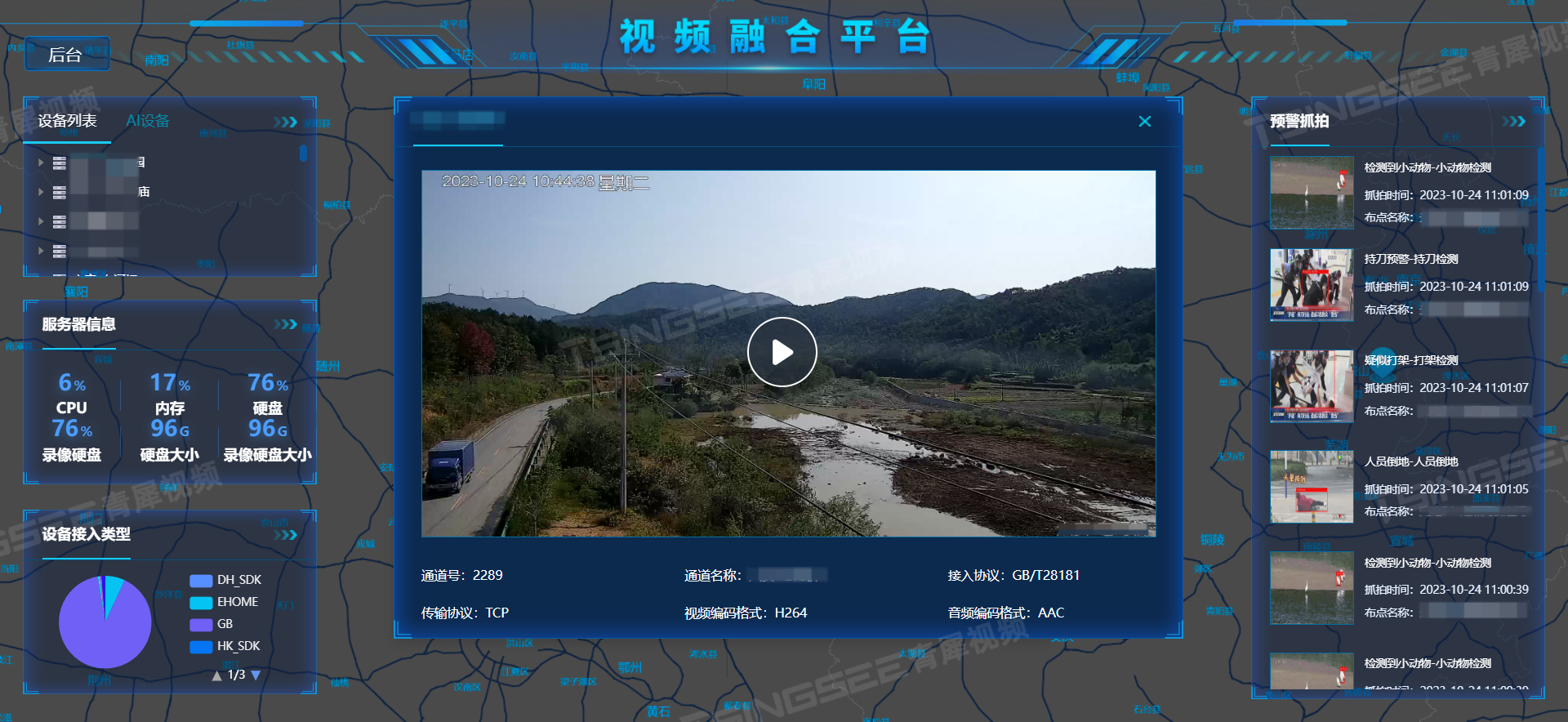
视频汇聚/音视频流媒体视频平台/视频监控EasyCVR分享页面无法播放,该如何解决?
国标GB28181安防视频监控/视频集中存储/云存储EasyCVR平台可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有国标GB28181、RTSP/Onvif、RTMP等,以及支持厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等。平台既具备传统…...

机器学习-逻辑回归
一、引言 逻辑回归(Logistic Regression)是一种广泛应用于分类问题的监督学习算法。尽管名字中含有“回归”二字,但这并不意味着它用于解决回归问题。相反,逻辑回归专注于解决二元或多元分类问题,如邮件是垃圾邮件还是…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...
