关于DNS服务器地址总是127.0.0.1且无法解析域名地址
问题
笔者尝试nslookup解释域名时，出现服务器变成本地环回口地址，导致无法解析域名
C:\Users\Zsy>nslookup www.baidu.com
服务器: UnKnown
Address: 127.0.0.1*** UnKnown 找不到 www.baidu.com: Server failed
排查思路
尝试关闭虚拟网卡，配死所有网卡dns ip通通无效。
通过以下命令看到，无论笔者怎么配置dns地址，配置中总会有一条127.0.0.1的地址在最上方
ipconfig /all
最终通过搜索引擎查到这样一个答案，原来是笔者连接公司网络时挂了easy connect导致
登录easyconnect 软件，链接VPN，DNS就会被改为127.0.0.1
解决方案
关掉easy connect问题得以解决
参考文献
登录easyconnect 软件，链接VPN，DNS就会被改为127.0.0.1
相关文章：
关于DNS服务器地址总是127.0.0.1且无法解析域名地址
问题 笔者尝试nslookup解释域名时，出现服务器变成本地环回口地址，导致无法解析域名 C:\Users\Zsy>nslookup www.baidu.com 服务器: UnKnown Address: 127.0.0.1*** UnKnown 找不到 www.baidu.com: Server failed排查思路 尝试关闭虚拟网卡&#…...
制作一个RISC-V的操作系统四-嵌入式开发介绍
文章目录 什么是嵌入式开发交叉编译查看一些GCC文件夹 调试器GDB相关语法命令 模拟器QEMUQEMU的安装和使用项目构造工具MakeMakeFile的构成make的运行 练习4-1练习4-2练习4-3 什么是嵌入式开发 程序跑到开发板上，或者说运行到硬件上 交叉编译 简单理解交叉编译来说…...
Python爬虫-实现批量抓取王者荣耀皮肤图片并保存到本地
前言 本文是该专栏的第12篇，后面会持续分享python爬虫案例干货，记得关注。 本文以王者荣耀的英雄皮肤为例，用python实现批量抓取“全部英雄”的皮肤图片，并将图片“批量保存”到本地。具体实现思路和详细逻辑，笔者将在正文结合完整代码进行详细介绍。注意，这里抓取的图片…...
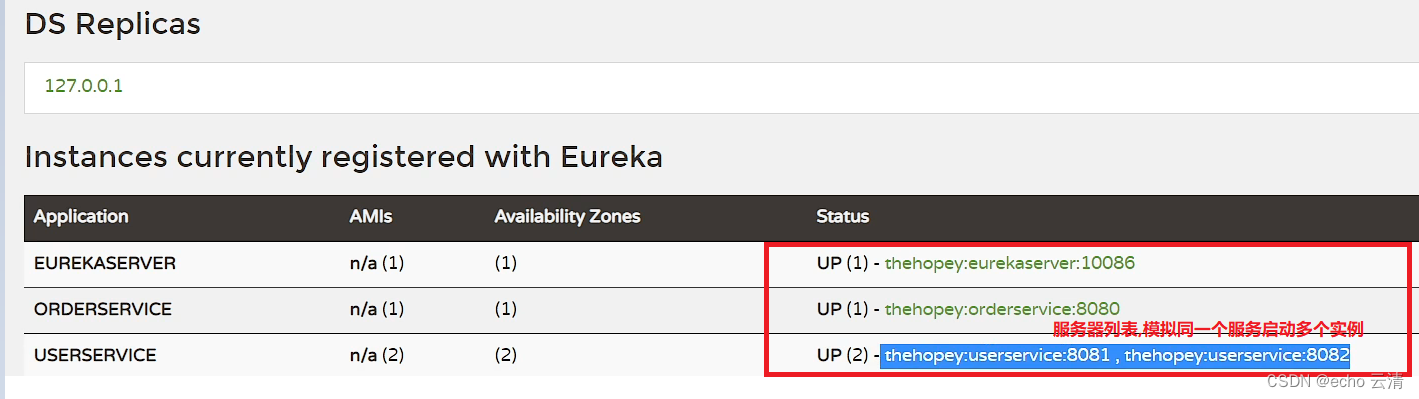
04-详解Eureka注册中心的作用,具体配置,服务注册和服务发现
Eureka注册中心的作用 Eureka架构 远程调用的两个问题 服务的ip地址和端口号写死: 生产环境中服务的地址可能会随时发生变化,如果写死每次都需要重新修改代码多实例问题: 在高并发的情况下一个服务可以有多个实例形成一个集群,此时如果采用硬编码的方式只能访问服务的一个实…...
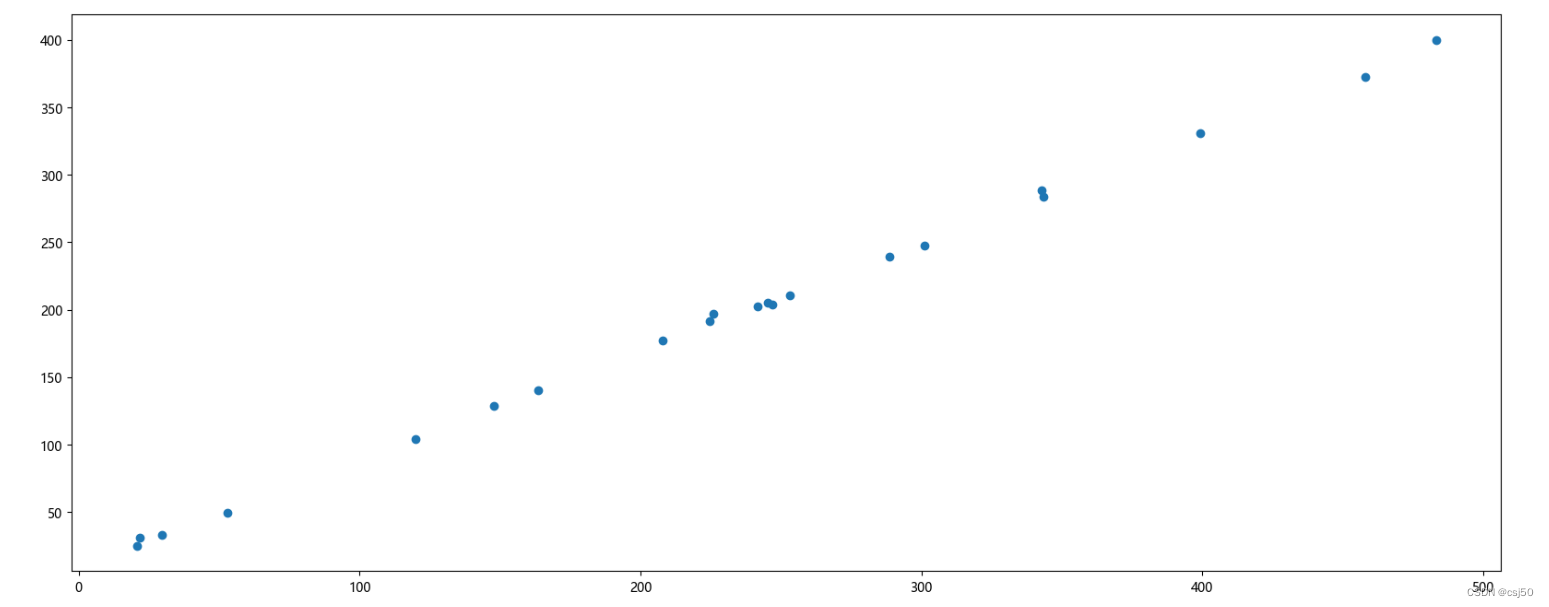
数据分析基础之《matplotlib（3）—散点图》
一、常见图形种类及意义 1、matplotlib能够绘制折线图、散点图、柱状图、直方图、饼图。我们需要知道不同的统计图的意义，以此来决定选择哪种统计图来呈现我们的数据 2、折线图plot 说明：以折线的上升或下降来表示统计数量的增减变化的统计图 特点&…...
Flask 动态路由、请求数据接收、视图函数返回值详解
一、动态路由 在前面的博客中，我们学习了如何创建基本的 Flask 应用，并定义了一些简单的路由。但有时候，我们需要更加灵活的路由，能够根据用户请求的不同来动态生成响应。Flask 提供了动态路由的功能，使我们能够轻松处…...
Transformer 简介
Transformer 是 Google 在 2017 年底发表的论文 Attention Is All You Need 中所提出的 seq2seq 模型。Transformer 模型的核心是 Self-Attention 机制，能够处理输入序列中的每个元素，并能计算其与序列中其他元素的交互关系的方法，从而能够更…...
)
LLVM学习笔记（64)
4.4.3.3.3. 设置寄存器类对类型的行为 1679行调用computeRegisterProperties()来计算寄存器类的衍生属性。TargetLoweringBase的容器RegisterTypeForVT、RegClassForVT以及NumRegistersForVT用于记录原生支持每个ValueType目标机器寄存器类的信息，即类型对应的寄存…...
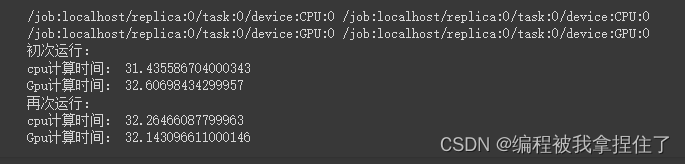
深度学习TensorFlow2基础知识学习前半部分
目录 测试TensorFlow是否支持GPU： 自动求导： 数据预处理 之 统一数组维度 定义变量和常量 训练模型的时候设备变量的设置 生成随机数据 交叉熵损失CE和均方误差函数MSE 全连接Dense层 维度变换reshape 增加或减小维度 数组合并 广播机制&#…...
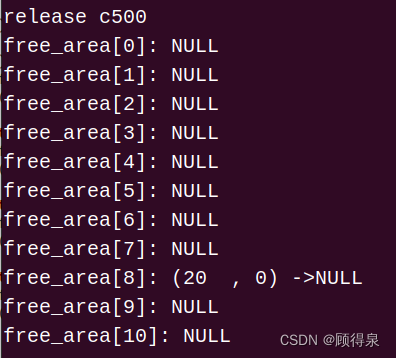
Linux系统---简易伙伴系统
顾得泉：个人主页 个人专栏：《Linux操作系统》 《C/C》 《LeedCode刷题》 键盘敲烂，年薪百万！ 一、题目要求 1.采用C语言实现 2.伙伴系统采用free_area[11]数组来组织。要求伙伴内存最小为一个页面，页面大小为4KB…...
Redis使用Lua脚本
Lua脚本 redis可以支持lua脚本，可以使用lua脚本来将几个命令整合为一个整体来执行，这样可以使得多个命令原子操作，且可以减少网络开销 Lua的数据类型 Lua是一个动态类型的语言，一个变量可以存储任何类型的值，类型有&am…...
macos安装metal 加速版 pytorch
categories: [Python] tags: Python MacOS 写在前面 试试 m3 的 metal 加速效果如何 Mac computers with Apple silicon or AMD GPUsmacOS 12.3 or laterPython 3.7 or laterXcode command-line tools: xcode-select --install 安装 Python: conda-forge brew install minif…...
【学习笔记】lyndon分解
摘抄自quack的ppt。 这部分和 s a sa sa的关联比较大，可以加深对 s a sa sa的理解。 Part 1 如果字符串 s s s的字典序在 s s s以及 s s s的所有后缀中是最小的，则称 s s s是一个 lyndon \text{lyndon} lyndon串。 lyndon \text{lyndon} lyndon分解&a…...
21、命令执行
文章目录 一、命令执行概述1.1 基本定义1.2 原理1.3 两个条件1.4 命令执行漏洞产生的原因1.5 管道符号和通用命令符 二、远程命令执行2.1 远程命令执行相关函数2.2 远程命令执行漏洞的利用 三、系统命令执行3.1 相关函数3.2 系统命令执行漏洞利用 四、命令执行漏洞防御 一、命令…...
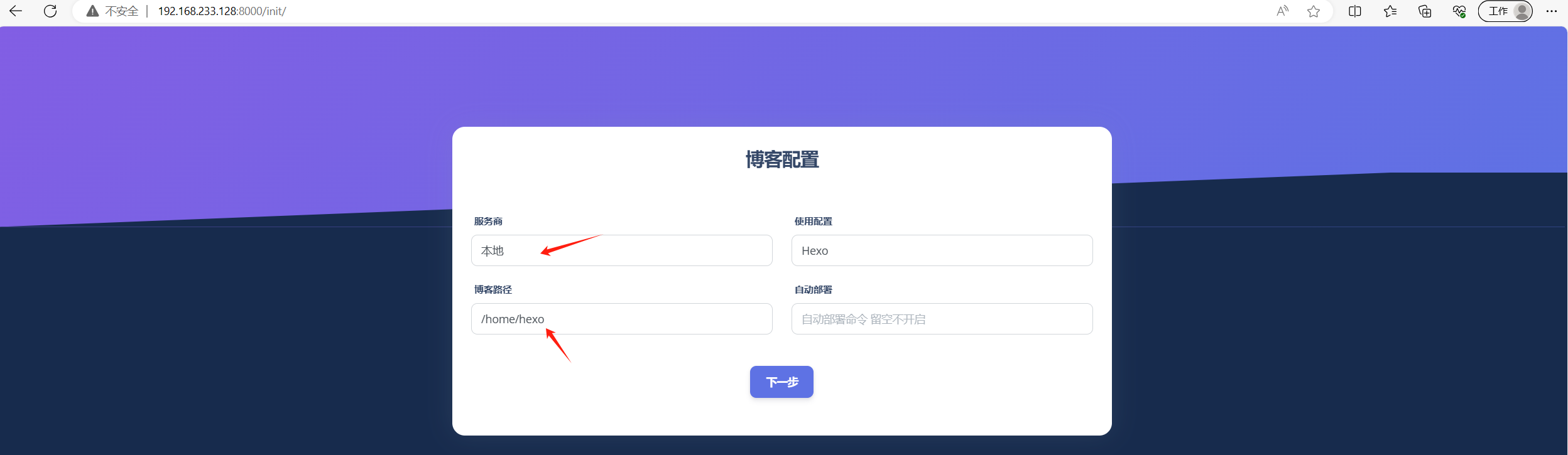
Qexo博客后台管理部署
Qexo博客后台管理部署 个人主页 个人博客 参考文档 https://www.oplog.cn/qexo/本地部署 采用本地Docker部署管理本地Hexo 下载代码包 若无法下载使用科学工具下载到本地在上传到服务器 wget https://github.com/Qexo/Qexo/archive/refs/tags/3.0.1.zip# 解压 unzip Qexo…...
最小生成树prim
最小生成树（三）Prim算法及存储结构_哔哩哔哩_bilibili 311 最小生成树 Prim 算法_哔哩哔哩_bilibili #include <iostream> #include <queue> #include <string> #include <stack> #include <vector> #include <set…...
实用篇 | 一文学会人工智能中API的Flask编写(内含模板)
----------------------- 🎈API 相关直达 🎈-------------------------- 🚀Gradio: 实用篇 | 关于Gradio快速构建人工智能模型实现界面，你想知道的都在这里-CSDN博客 🚀Streamlit :实用篇 | 一文快速构建人工智能前端展…...
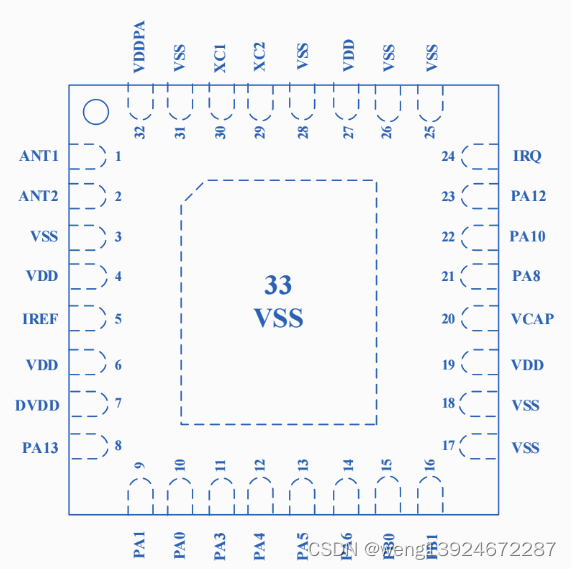
Si24R03—低功耗 SOC 芯片（集成RISC-V内核+2.4GHz无线收发器）
Si24R03是一款高度集成的低功耗SOC芯片，其集成了基于RISC-V核的低功耗MCU和工作在2.4GHz ISM频段的无线收发器模块。 MCU模块具有低功耗、Low Pin Count、宽电压工作范围，集成了13/14/15/16位精度的ADC、LVD、UART、SPI、I2C、TIMER、WUP、IWDG、RTC等丰…...
C# Winform 日志系统
目录 一、效果 1.刷新日志效果 2.单独日志的分类 3.保存日志的样式 二、概述 三、日志系统API 1.字段 Debug.IsScrolling Debug.Version Debug.LogMaxLen Debug.LogTitle Debug.IsConsoleShowLog 2.方法 Debug.Log(string) Debug.Log(string, params object[]) …...
【Java 基础】27 XML 解析
文章目录 1.SAX 解析器1）什么是 SAX2）SAX 工作流程初始化实现事件处理类解析 3）示例代码 2.DOM 解析器1）什么是 DOM2）DOM 工作流程初始化解析 XML 文档操作 DOM 树 3）示例代码 总结 在项目开发中࿰…...
Cursor实现用excel数据填充word模版的方法
cursor主页：https://www.cursor.com/ 任务目标：把excel格式的数据里的单元格，按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例，…...
CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO：支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题：MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者：Yanyuan Chen, Dexuan Xu, Yu Hu…...
visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中，选择 环境 -> 常规 ，将其中的颜色主题改成深色 点击确定，更改完成...
pam_env.so模块配置解析
在PAM（Pluggable Authentication Modules）配置中， /etc/pam.d/su 文件相关配置含义如下： 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块，负责验证用户身份&am…...
数据库分批入库
今天在工作中，遇到一个问题，就是分批查询的时候，由于批次过大导致出现了一些问题，一下是问题描述和解决方案： 示例： // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...
自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效，它能挖掘数据中的时序信息以及语义信息，但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN，但是…...
让回归模型不再被异常值“带跑偏“，MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中，损失函数的选择对模型性能具有决定性影响。均方误差（MSE）作为经典的损失函数，在处理干净数据时表现优异，但在面对包含异常值的噪声数据时，其对大误差的二次惩罚机制往往导致模型参数…...
4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式，自动确定它们的类型。 这一特性减少了显式类型注解的需要，在保持类型安全的同时简化了代码。通过分析上下文和初始值，TypeSc…...
MySQL 主从同步异常处理
阅读原文：https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主，遇到的这个错误： Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一，通常表示ÿ…...
论文阅读：LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址：LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂，正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...