2021年第十届数学建模国际赛小美赛A题气道阻力的评估解题全过程文档及程序
2021年第十届数学建模国际赛小美赛
A题 气道阻力的评估
原题再现:
气道阻力的定义是通过肺气道产生单位气流所需的经肺压力的变化。更简单地说,它是嘴和肺泡之间的压力差,除以气流。影响气道阻力的因素是多方面的,我们需要探讨这些因素是如何影响气道总阻力的。
许多研究假设肺气道是一个光滑的相邻圆柱体系统,空气以层流方式流经该系统,其结果基于稳定流动的假设。这种假设与实际情况有许多不一致之处。例如,鼻气道阻力占总气道阻力的50%以上,但鼻腔不是圆柱形的。这种假设完全忽略了上气道的紊流。因此,预测气道的总通气量是不够的。
我们需要建立一个模型来估计总气道阻力至少由这些因素:气流速度,肺容量,以及气道各部分的横截面积。这些是一些最重要的促成因素。对于某些患者,由于手术等原因,气道的某些部分会暂时/永久改变,包括某些部分的形状或横截面积。我们的模型将用于评估患者气道的通气性能,并帮助医生设计对气道总通气性能影响最小的治疗方案。
整体求解过程概述(摘要)
气道阻力定义为产生单位气流通过肺气道所需的跨肺压力变化。气道阻力的大小间接反映了患者的气道通气性能。因此,有必要找出影响气道总阻力的因素。
在问题的第一部分,根据流体力学方程,得到了口与肺泡压差、气道长度、气道各截面截面积等因素之间的关系,进而得到气道总阻力的表达式。由于气体可能具有一定的粘度,通过计算不考虑气体粘度的伯努利方程和分别考虑气体粘度的伯努利方程,可以得到压差与其它因素的关系。计算气道各节段的气流速度和口肺泡与肺的压差。在具体的计算中,采用蒙特卡罗模拟的方法,计算出气道各截面的一些物理量。最后根据气道阻力的定义计算气道阻力。在不考虑气体粘度和考虑气体粘度的情况下,利用MATLAB绘制了两种情况的比较图。通过比较,最终得到考虑气体粘度条件下的气道阻力。
在问题的第二部分,根据呼吸系统的压力-容积曲线(拟合结果为s型曲线),压差与肺容积之间的关系可用指数函数来描述。然后,利用上一问题中的方法和MATLAB计算了气道内的平均气体流量。通过定义气道阻力,得到气道阻力与肺容量的关系曲线(其他变量在此控制不变)。
并利用MATLAB控制其他变量,绘制气道阻力与气道各截面面积的关系曲线。通过观察关系曲线,可以得出对全气道通气性能影响不大的治疗方案。
在此基础上,总结了气道阻力的影响因素和物理表现,并得到了相应的微分方程。
模型假设:
(1) 由于气体的粘度非常小,因此未考虑气体粘度对气道阻力估计值的影响。
(2) 当倾斜时,气体重力引起的倾斜角对压力的影响被忽略。
(3) 由于人气道的每一段的横截面积可以变化,因此假设人气道的表面是平滑的曲面(不一定是圆柱形的),并且气道的每一段的横截面积满足正态分布。
(4) 当气道的段数足够大时,假设每个段中的压差与每个段的长度成线性关系,即从气道的一个段到嘴的压差与它们之间的距离(深度)成线性关系。
(5) 其他阻力对气道阻力估计的影响被忽略。
(6) 假设气体密度不随气道深度变化,且气体密度p=1.293kg/m3为常数。
问题重述:
气道阻力可能受到许多不确定因素的影响,如气流速度、肺容量和每个气道段的横截面积。所以我们需要讨论这些因素是如何影响总气道阻力的。许多研究假设肺气道是一个光滑的连接柱体系统,空气以层流方式流过该系统,其结果基于稳定流动的假设。这种假设与实际情况有许多不一致之处。例如,鼻气道阻力占总气道阻力的50%以上,但鼻腔不是圆柱形的。这种假设完全忽略了上气道的紊流。因此,我们需要建立一个模型来描述影响气道阻力的因素。
1气流速度与气道阻力的关系
气道速度和气道阻力之间的关系是什么?如何利用曲线分析这些因素对气道阻力的影响?
为了解决这类问题,我们需要找到一个合适的物理模型来描述这些物理量之间的关系。由于该问题是以气体(属于流体)为基础的,因此需要用流体力学方程来描述这些物理量之间的关系·首先,通过对伯努利方程进行变形,得到了相应的微分方程形式和气道各段气速、压差的递推公式。当然,也可以得到肺泡附近的气流速度与肺泡与口部的压差和初始气流速度之间的关系。然后,利用递推公式在MATLAB中进行蒙特卡罗仿真,并进行一定次数的迭代,使气道的每个截面都能近似光滑圆柱体,从而使数值接近真实值。最后,通过MATLAB绘图分析气道阻力与其他因素的关系。
·由于以前没有考虑空气粘度对气道内其他物理量的影响,本文对伯努利方程进行了修正,采用粘性流体伯努利方程求解。重复刚才的操作,在MATLAB上绘制图形,比较考虑粘性和不考虑粘性两种情况,最后选择考虑粘性的Bernoulli方程方案求解。
2肺容量与气道阻力的关系
肺容量和气道阻力之间的关系是什么?
由于气道阻力是嘴和肺泡之间的压差与气道中气流的比率,因此问题可分为两部分:
1) 探讨肺动脉压差与肺容量的关系。
2) 通过以上两种关系间接探讨气道阻力与肺容量的关系。因此,通过寻找信息,我们找到了适合描述肺容积与压差关系的曲线:呼吸系统压力容积曲线。
3横截面积与气道阻力的关系
气道各部分的横截面积与气道阻力之间的关系是什么?
根据第一个主题的方法,通过控制其他变量不变,探索气道阻力与气道各部分横截面积之间的关系。利用MATLAB软件分析了两者之间的关系。
4如何评估患者的气道性能
通气性能通常与气道阻力有关。因此,有必要探讨通气性能与气道阻力的相关性,并通过得出的结论对通气性能进行评价。
5对全气道通气性能影响最小的方案
对于某些患者,由于手术或其他原因,气道的某些部分可能会暂时/永久改变,包括某些部分的形状或横截面积。因此,可将该问题转化为以下问题:选择与术前横截面积差值最小的合适横截面积,使该面积下的气道阻力差值小于术前。
通过分析第三个问题中气道阻力与横截面积的关系曲线,可以确定引起气道阻力微小变化的横截面积(横截面积应尽可能接近原始横截面积)。
模型的建立与求解整体论文缩略图


全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
部分程序代码:(代码和文档not free)
function mean_p_airway=non_viscosity(dp,H,N)
v0=14.8e-6;
g=9.8;
ru=1.293;
p_airway=zeros(1,length(N));
for i=1:length(N)
v2=[v0^2,zeros(1,N(i))];
S=zeros(1,N(i));
for j=1:N(i)
S(j)=(0.0125^2*normrnd(1,rand(1)))*1e-2;
v2(j+1)=2/ru*(dp/N(i)-ru*g*H/N(i))+v2(j);
end
p_airway(i)=dp/mean(abs(sqrt(v2(2:end))).*S);
end
mean_p_airway=mean(p_airway);
end
function mean_p_airway=airway_resistance(dp,H,N0)
v0=14.8e-6;
g=9.8;
ru=1.293;
mu=0.01894;
p_airway=zeros(1,length(N0));
for N=N0
v2=[v0^2,zeros(1,N)];
S=zeros(1,N);
for i=1:N
S(i)=(0.0125^2*normrnd(1,rand(1)))*1e-2;
v2(i+1)=2/ru*(dp/N-ru*g*H/N-8*pi*mu*sqrt(v2(i))*H/(N*g*S(i)));
end
p_airway((N-N0(1))/(N0(2)-N0(1))+1)=dp/mean(abs(sqrt(v2(2:end))).*S);
end
mean_p_airway=mean(p_airway);
end
clear;clc;close all
p0=1.013e5;
v0=14.8e-6;
g=9.8;
ru=1.293;
mu=0.01894;
lN=input('Please enter the lower limit of monte Carlo simulation:');
uN=input('Please enter the maximum number of Monte Carlo simulations:');
N=lN:uN;
dp=100:300;
airway=zeros(1,length(dp));
mean_p_airway=zeros(1,length(dp));
for i=1:length(dp)
airway(i)=non_viscosity(dp(i),0.12,N);
mean_p_airway(i)=airway_resistance(dp(i),0.12,N);
end
figure(1)
plot(dp,airway,'r-p',dp,mean_p_airway,'b-*')
xlabel('differential pressure/Pa')
ylabel('airway resistance/Pa*m^{-3}*s')
legend('without the viscosity of the air','with the viscosity of the air')
figure(2)
plot(dp,airway,'r-p')
xlabel('differential pressure/Pa')
ylabel('airway resistance/Pa*m^{-3}*s')
figure(3)
plot(dp,mean_p_airway,'b-*')
xlabel('differential pressure/Pa')
ylabel('airway resistance/Pa*m^{-3}*s')
H=0.11:0.001:0.13;
airway=zeros(1,length(H));
mean_p_airway=zeros(1,length(H));
for i=1:length(H)
airway(i)=non_viscosity(200,H(i),N);
mean_p_airway(i)=airway_resistance(200,H(i),N);
end
figure(4)
plot(H,airway,'r-x',H,mean_p_airway,'-*')
xlabel('The length of the airway/m')
ylabel('airway resistance/Pa*m^{-3}*s')
legend('without the viscosity of the air','with the viscosity of the air')
figure(5)
plot(H,airway,'r-x')
xlabel('The length of the airway/m')
ylabel('airway resistance/Pa*m^{-3}*s')
figure(6)
plot(H,mean_p_airway,'-*')
xlabel('The length of the airway/m')
ylabel('airway resistance/Pa*m^{-3}*s')
全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
相关文章:

2021年第十届数学建模国际赛小美赛A题气道阻力的评估解题全过程文档及程序
2021年第十届数学建模国际赛小美赛 A题 气道阻力的评估 原题再现: 气道阻力的定义是通过肺气道产生单位气流所需的经肺压力的变化。更简单地说,它是嘴和肺泡之间的压力差,除以气流。影响气道阻力的因素是多方面的,我们需要探讨这…...

内网环境安装K8S1.20.11版本集群
目录 第一章.实验要求和环境 1.1.实验要求 1.2.实验环境 1.3.依赖关系处理 第二章.K8S的安装过程 2.1.初始化到集群安装成功 ------------------------------ 环境准备 ------------------------------ docker安装好了后 2.2.安装K8组件 -------------------- 部署K8…...

【前端设计模式】之策略模式
概述 在前端开发中,我们经常会遇到需要根据不同的条件或情况来执行不同的算法或行为的情况。这时,策略模式就能派上用场。策略模式是一种行为型设计模式,它将不同的算法封装成独立的策略对象,使得这些算法可以互相替换࿰…...
JUC包(面试常问)
1. Callable接口 类似于Runnable接口,Runnable描述的任务,不带返回值;Callable描述的任务带返回值。 public class Test {//创建线程,计算12...1000public static void main(String[] args) throws ExecutionException, Interru…...

文字处理工具Word mac软件特点
Microsoft Word mac是一款文字处理软件。它是 Microsoft office 套件的一部分,已广泛用于创建、编辑和格式化文本文档。 Word mac软件特点 改进的协作工具:使用 Microsoft Word 2021,多个用户可以同时处理一个文档,从而更轻松地与…...
把 Windows 11 装进移动硬盘:Windows 11 To Go
本篇文章聊聊如何制作一个可以“说带走就带走”的 Windows 操作系统,将 Windows11 做成能够放在 U 盘或者移动硬盘里的 WinToGo “绿色软件”。 写在前面 在《开源的全能维护 U 盘工具:Ventoy》这篇文章的最后,我提到了一个关键词 “WinToG…...

11、pytest断言预期异常
官方用例 # content of test_exception_zero.py import pytestdef test_zero_division():with pytest.raises(ZeroDivisionError):1/0# content of test_exception_runtimeerror.py import pytestdef test_recursion_depth():with pytest.raises(RuntimeError) as excinfo:def…...

Vue之数据绑定
在我们Vue当中有两种数据绑定的方法 1.单向绑定 2.双向绑定 让我为大家介绍一下吧! 1、单向绑定(v-bind) 数据只能从data流向页面 举个例子: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"…...

druid在没有web的项目中如何查看监控
(1)在这个网址下载druidStat.bat文件https://github.com/alibaba/druid/blob/master/core/src/main/scripts/druidStat.bat druidStat.bat文件内容如下: echo offset _RUNJAVA"%JAVA_HOME%\bin\java.exe" set _TOOLSJAR"%JA…...

游戏被攻击该怎么办?游戏盾该如何使用,游戏盾如何防护攻击
随着Internet互联网络带宽的增加和多种DDOS黑客工具的不断发布,DDOS拒绝服务攻击的实施越来越容易,DDOS攻击事件正在成上升趋势。出于商业竞争、打击报复和网络敲诈等多种因素,导致很多商业站点、游戏服务器、聊天网络等网络服务商长期以来一…...
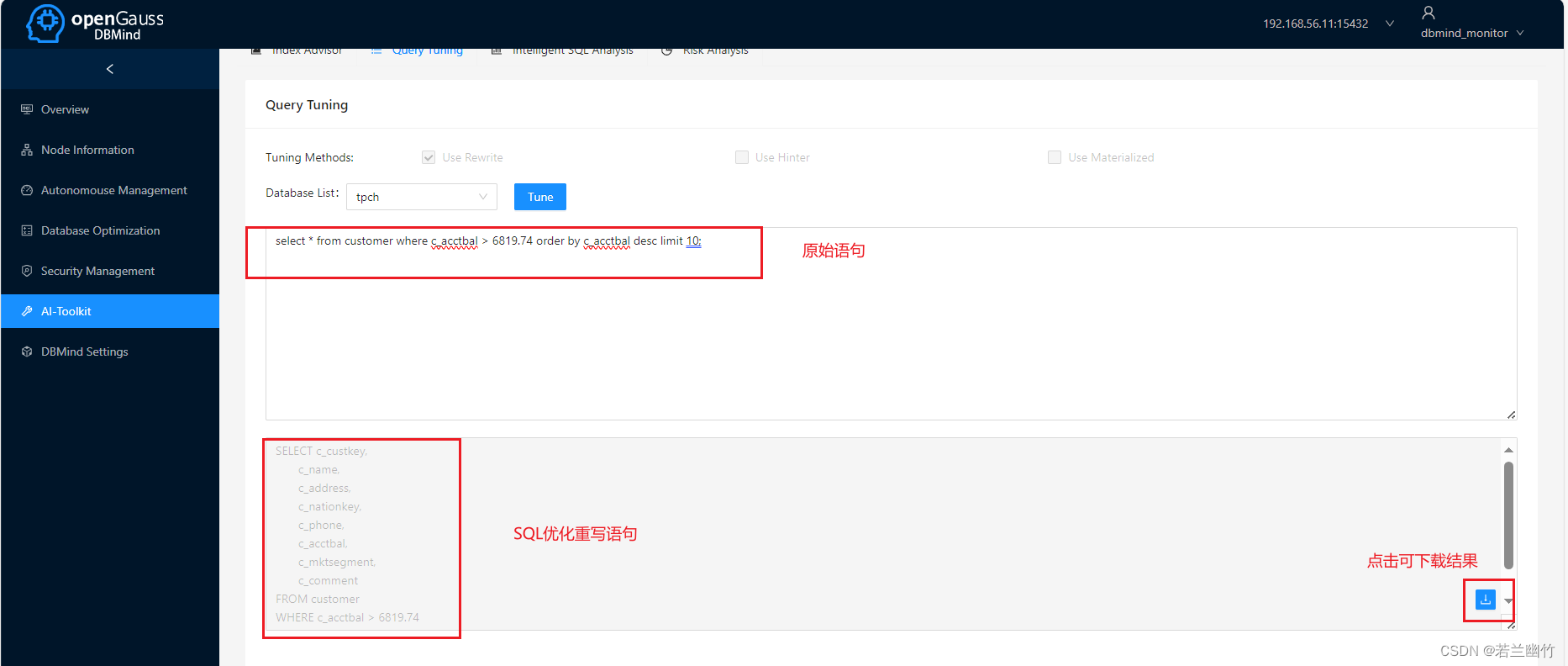
【基于openGauss5.0.0简单使用DBMind】
基于openGauss5.0.0简单使用DBMind 一、环境说明二、初始化tpch测试数据三、使用DBMind索引推荐功能四、使用DBMind实现SQL优化功能 一、环境说明 虚拟机:virtualbox操作系统:openEuler 20.03 TLS数据库:openGauss-5.0.0DBMind:d…...
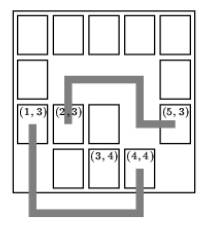
[递归回溯]连接卡片最短路径
小游戏 题目描述 一天早上,你起床的时候想:“我编程序这么牛,为什么不能靠这个挣点银子呢?”因此你决定编写一个小游戏。 游戏在一个分割成w * h个长方格子的矩形板上进行。如图所示,每个长方格子上可以有一张游戏…...

初识人工智能,一文读懂强化学习的知识文集(5)
🏆作者简介,普修罗双战士,一直追求不断学习和成长,在技术的道路上持续探索和实践。 🏆多年互联网行业从业经验,历任核心研发工程师,项目技术负责人。 🎉欢迎 👍点赞✍评论…...
视频封面提取:精准截图,如何从指定时长中提取某一帧图片
在视频制作和分享过程中,一个有吸引力的封面或截图往往能吸引更多的观众点击观看。有时候要在特定的时间段内从视频中提取一帧作为封面或截图。如果每个视频都手动提取的话就会耗费很长时间,那么如何智化能批量提取呢?现在一起来看下云炫AI智…...

Shopify 开源 WebAssembly 工具链 Ruvy
最近,Spotify 开源了Ruvy,一个 WebAssembly 工具链,能够将 Ruby 代码转换为 Wasm 模块。Ruvy 基于ruby.wasm, 用 Rust 实现,提升了性能并简化了 Wasm 模块的执行。 Ruvy 利用了ruby.wasm提供的 Ruby 解释器模块,并使用wasi-vfs (WASI 虚拟文件系统)将其与所有指定的 Rub…...

zxjy008- 项目集成Swagger
Swagger可以生成在线文档,还可以进行接口测试。 1、创建common模块(maven类型) 为了让所有的微服务子子模块都可以使用,可以在guli_parent父工程下面创建公共模块 1.1 在guli_parent父工程下面创建公共模块 配置: groupId:com…...

使用linux CentOS本地部署SQL Server数据库
🌈个人主页:聆风吟 🔥系列专栏:数据结构、Cpolar杂谈 🔖少年有梦不应止于心动,更要付诸行动。 文章目录 📋前言一. 安装sql server二. 局域网测试连接三. 安装cpolar内网穿透四. 将sqlserver映射…...
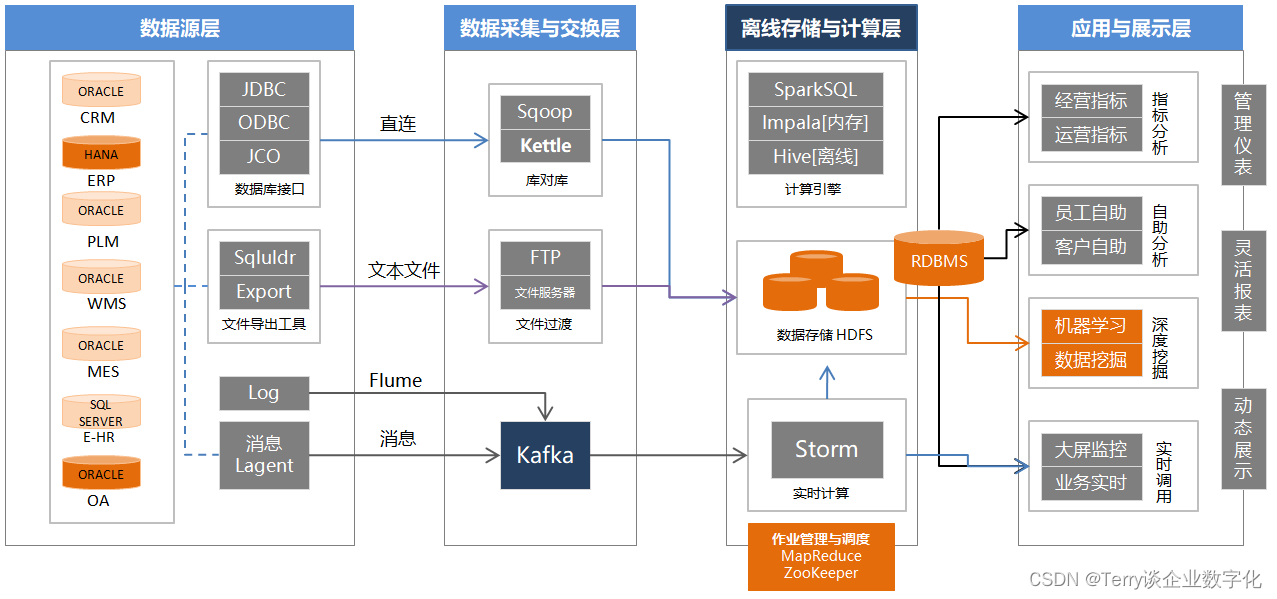
理解基于 Hadoop 生态的大数据技术架构
转眼间,一年又悄然而逝,时光荏苒,岁月如梭。当回首这段光阴,不禁感叹时间的匆匆,仿佛只是一个眨眼的瞬间,一年的旅程已成为过去,而如今又到了画饼的时刻了 ! 基于 Hadoop 生态的大数…...

【Go】Go语言基础内容
变量声明: 变量声明:在Go中,变量必须先声明然后再使用。声明变量使用 var 关键字,后面跟着变量名和类型,如下所示: var age int这行代码声明了一个名为 age 的整数变量。 变量初始化:您可以在声…...

HP-UNIX 系统安全基线 安全加固操作
目录 账号管理、认证授权 账号 ELK-HP-UX-01-01-01 ELK -HP-UX-01-01-02 ELK -HP-UX-01-01-03 ELK-HP-UX-01-01-04 ELK-HP-UX-01-01-05 口令 ELK-HP-UX-01-02-01 ELK-HP-UX-01-02-02 ELK-HP…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...
