基于Html+腾讯云播SDK开发的m3u8播放器
周末业余时间在家无事,学习了一下腾讯的云播放sdk,并制作了一个小demo(m3u8播放器),该在线工具是基于腾讯的云播sdk开发的,云播sdk非常牛,可以支持多种播放格式。
预览地址
m3u8player.org
源码地址
https://github.com/geeeeeeeek/m3u8player
开发步骤
第一步:集成播放器SDK:
播放器 SDK 支持 cdn 集成方式:
<link href="https://web.sdk.qcloud.com/player/tcplayer/release/v5.1.0/tcplayer.min.css" rel="stylesheet"/><!--播放器脚本文件--><script src="https://web.sdk.qcloud.com/player/tcplayer/release/v5.1.0/tcplayer.v5.1.0.min.js"></script>
第二步:设置容器
然后,设置播放器容器,在需要展示播放器的页面位置加入播放器容器。可以在 index.html 中加入如下代码(容器 ID 以及宽高都可以自定义)。
<video id="player-container-id" width="414" height="270" preload="auto" playsinline webkit-playsinline>
</video>
第三步:初始化并播放
var player = TCPlayer('player-container-id', {sources: [{src: 'path/to/video',}],licenseUrl: 'https://license-url',
}); // player.src(url); // url 播放地址
最终集成后的代码可以参考:
https://github.com/geeeeeeeek/m3u8player
附:m3u8知识
M3U8是一种播放多媒体列表的文件格式,它的设计初衷是为了播放音频文件,比如MP3,但是越来越多的软件现在用来播放视频文件列表,M3U8也可以指定在线流媒体音频源。很多播放器和软件都支持M3U8文件格式。
相关文章:

基于Html+腾讯云播SDK开发的m3u8播放器
周末业余时间在家无事,学习了一下腾讯的云播放sdk,并制作了一个小demo(m3u8播放器),该在线工具是基于腾讯的云播sdk开发的,云播sdk非常牛,可以支持多种播放格式。 预览地址 m3u8player.org 源码…...

uniapp小程序分享为灰色
引用:https://www.cnblogs.com/panwudi/p/17074172.html uniapp开发的微信小程序,没有转发,分享: 创建一个mixin:common/share.js export default {onShareAppMessage(res) { //发送给朋友return {}},onShareTimeline(res) {//…...
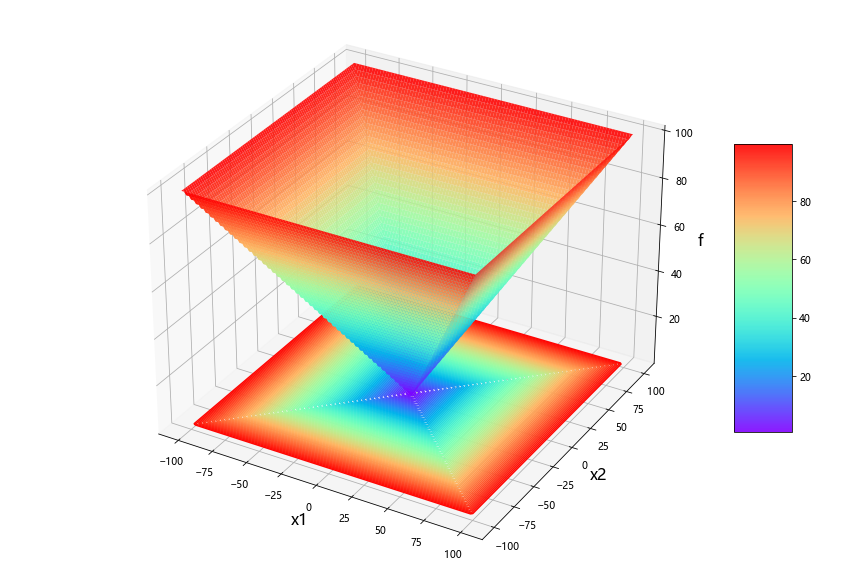
python:五种算法(OOA、WOA、GWO、PSO、GA)求解23个测试函数(python代码)
一、五种算法简介 1、鱼鹰优化算法OOA 2、鲸鱼优化算法WOA 3、灰狼优化算法GWO 4、粒子群优化算法PSO 5、遗传算法GA 二、5种算法求解23个函数 (1)23个函数简介 参考文献: [1] Yao X, Liu Y, Lin G M. Evolutionary programming made…...

DIP——添加运动模糊与滤波
1.运动模糊 为了模拟图像退化的过程,在这里创建了一个用于模拟运动模糊的点扩散函数,具体模糊的方向取决于输入的motion_angle。如果运动方向接近水平,则模糊效果近似水平,如果运动方向接近垂直,则模糊效果近似垂直。具…...
——SQL处理过程)
SQL Server查询计划(Query Plan)——SQL处理过程
6. 查询计划(Query Plan) 6.1. SQL处理过程 就SQL语句的处理过程而言,各关系库间大同小异,尤其是商业库之间实现机制和细节差别更小些,其功能及性能支持方面也更加强大和完善。SQL Server作为商业库中的后起之秀,作为SQL语句处理过程的主要支撑和保障,其优化器及相关机…...

【动手学深度学习】(十二)现代卷积神经网络
文章目录 一、深度卷积神经网络AlexNet1.理论知识 一、深度卷积神经网络AlexNet 1.理论知识 ImageNet(2010) 图片自然物体的彩色图片手写数字的黑色图片大小468 * 38728*28样本数1.2M60K类数100010 AlexNet AlexNet赢了2012ImageNet竞赛更深更大的LeNet主要改进ÿ…...
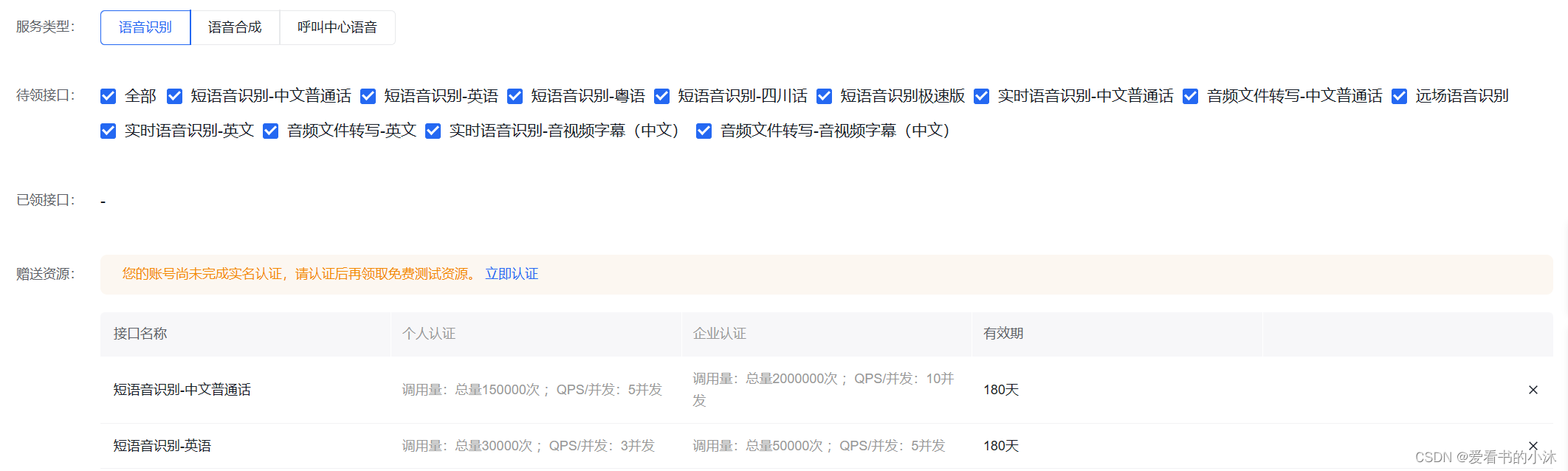
【小沐学Python】Python实现TTS文本转语音(speech、pyttsx3、百度AI)
文章目录 1、简介2、Windows语音2.1 简介2.2 安装2.3 代码 3、pyttsx33.1 简介3.2 安装3.3 代码 4、ggts4.1 简介4.2 安装4.3 代码 5、SAPI6、SpeechLib7、百度AI8、百度飞桨结语 1、简介 TTS(Text To Speech) 译为从文本到语音,TTS是人工智能AI的一个模组…...

TCP通信
第二十一章 网络通信 本章节主要讲解的是TCP和UDP两种通信方式它们都有着自己的优点和缺点 这两种通讯方式不通的地方就是TCP是一对一通信 UDP是一对多的通信方式 接下来会一一讲解 TCP通信 TCP通信方式呢 主要的通讯方式是一对一的通讯方式,也有着优点和缺点…...
2023济南大学acm新生赛题解
通过答题情况的难度系数: 签到:ACI 铜牌题:BG 银牌题:EF 金牌题:DHJKO 赛中暂未有人通过:LMNP A - AB Problem 直接根据公式计算就行。 #include<stdio.h> int main(){int a,b;scanf("%…...

docker-compose安装教程
1.确认docker-compose是否安装 docker-compose -v如上图所示表示未安装,需要安装。 如上图所示表示已经安装,不需要再安装,如果觉得版本低想升级,也可以继续安装。 2.离线安装 下载docker-compose安装包,上传到服务…...
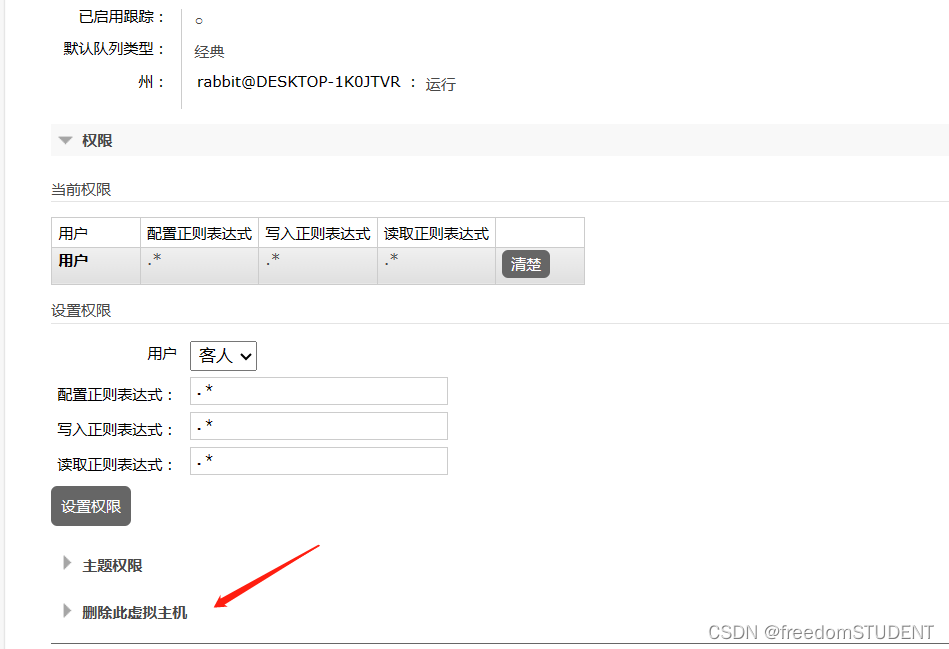
【rabbitMQ】rabbitMQ用户,虚拟机地址(添加,修改,删除操作)
rabbitMQ的下载,安装和配置 https://blog.csdn.net/m0_67930426/article/details/134892759?spm1001.2014.3001.5502 rabbitMQ控制台模拟收发消息 https://blog.csdn.net/m0_67930426/article/details/134904365?spm1001.2014.3001.5502 目录 用户 添加用户…...

Python高级算法——动态规划
Python中的动态规划:高级算法解析 动态规划是一种解决多阶段决策问题的数学方法,常用于优化问题。它通过将问题分解为子问题,并在解决这些子问题的基础上构建全局最优解。在本文中,我们将深入讲解Python中的动态规划,…...

MySQL在Centos7环境安装
说明: • 安装与卸载中,⽤⼾全部切换成为root,⼀旦 安装,普通⽤⼾能使⽤的 1. 卸载不要的环境 [roothcss-ecs-1036 ~]# ps ajx |grep mariadb # 先检查是否有mariadb存在 13134 14844 14843 13134 pts/0 14843 S 1005 0:00 gr…...

halcon视觉缺陷检测常用的6种方法
一、缺陷检测综述 缺陷检测是视觉需求中难度最大一类需求,主要是其稳定性和精度的保证。首先常见缺陷:凹凸、污点瑕疵、划痕、裂缝、探伤等。常用的手法有六大金刚(在halcon中的ocv和印刷检测是针对印刷行业的检测,有对应算子封装): 1.blob+特征 2.blob+差分+特征 3.光度…...

openGauss学习笔记-151 openGauss 数据库运维-备份与恢复-物理备份与恢复之gs_basebackup
文章目录 openGauss学习笔记-151 openGauss 数据库运维-备份与恢复-物理备份与恢复之gs_basebackup151.1 背景信息151.2 前提条件151.3 语法151.4 示例151.5 从备份文件恢复数据 openGauss学习笔记-151 openGauss 数据库运维-备份与恢复-物理备份与恢复之gs_basebackup 151.1 …...

报错:Uncaught ReferenceError: Cannot access ‘l‘ before initialization
在文件 .babelrc 或 babel.config.js ,webpack.config.js 下配置 .babel 或 babel.config.js "plugins": ["babel/plugin-transform-runtime" ] webpack.config.js,详见 Webpack target module.exports {target: [web, es5], }...

计算机视觉-机器学习-人工智能顶会 会议地址
计算机视觉-机器学习-人工智能顶会 会议地址 最近应该要整理中文资料的参考文献,很多会议文献都需要补全会议地点(新国标要求)。四处百度感觉也挺麻烦的,而且没有比较齐全的网站可以搜索。因此自己整理了一下计算机视觉-机器学习…...
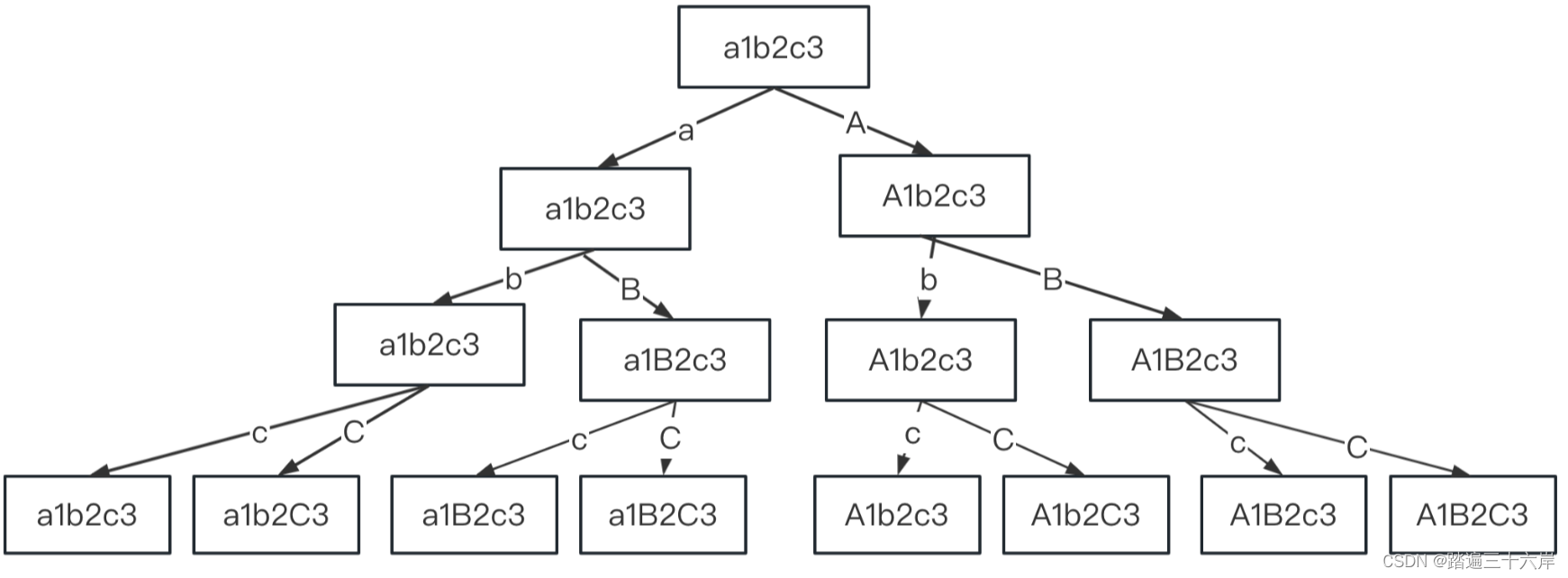
784. 字母大小写全排列
字母大小写全排列 描述 : 给定一个字符串 s ,通过将字符串 s 中的每个字母转变大小写,我们可以获得一个新的字符串。 返回 所有可能得到的字符串集合 。以 任意顺序 返回输出。 题目 : LeetCode 784.字母大小写全排列 : 784. 字母大小写全排列 分析…...
HarmonyOS鸿蒙应用开发——HTTP网络访问与封装
文章目录 基本使用封装参考 基本使用 鸿蒙应用发起HTTP请求的基本使用,如下: 导入http模块创建httpRequest对象发起http请求,并处理响应结果 第一、导入http模块: import http from ohos.net.http第二、创建httpRequest对象&a…...

vscode 编写爬虫爬取王者荣耀壁纸
网上关于爬虫大部分教程和编辑器用的都不是vscode ,此教程用到了vscode、Python、bs4、requests。 vscode配置Python安装环境可以看看这个大佬的教程 03-vscode安装和配置_哔哩哔哩_bilibili vscode配置爬虫环境可以参考这个大佬的教程【用Vscode实现简单的python…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

FOPLP vs CoWoS
以下是 FOPLP(Fan-out panel-level packaging 扇出型面板级封装)与 CoWoS(Chip on Wafer on Substrate)两种先进封装技术的详细对比分析,涵盖技术原理、性能、成本、应用场景及市场趋势等维度: 一、技术原…...

Python的__call__ 方法
在 Python 中,__call__ 是一个特殊的魔术方法(magic method),它允许一个类的实例像函数一样被调用。当你在一个对象后面加上 () 并执行时(例如 obj()),Python 会自动调用该对象的 __call__ 方法…...

「Java基本语法」变量的使用
变量定义 变量是程序中存储数据的容器,用于保存可变的数据值。在Java中,变量必须先声明后使用,声明时需指定变量的数据类型和变量名。 语法 数据类型 变量名 [ 初始值]; 示例:声明与初始化 public class VariableDemo {publi…...

Qt Quick Controls模块功能及架构
Qt Quick Controls是Qt Quick的一个附加模块,提供了一套用于构建完整用户界面的UI控件。在Qt 6.0中,这个模块经历了重大重构和改进。 一、主要功能和特点 1. 架构重构 完全重写了底层架构,与Qt Quick更紧密集成 移除了对Qt Widgets的依赖&…...

el-amap-bezier-curve运用及线弧度设置
文章目录 简介示例线弧度属性主要弧度相关属性其他相关样式属性完整示例链接简介 el-amap-bezier-curve 是 Vue-Amap 组件库中的一个组件,用于在 高德地图 上绘制贝塞尔曲线。 基本用法属性path定义曲线的路径,可以是多个弧线段的组合。stroke-weight线条的宽度。stroke…...
