【概率方法】重要性采样
从一个极简分布出发
假设我们有一个关于随机变量 X X X 的函数 f ( X ) f(X) f(X),满足如下分布
| p ( X ) p(X) p(X) | 0.9 | 0.1 |
|---|---|---|
| f ( X ) f(X) f(X) | 0.1 | 0.9 |
如果我们要对 f ( X ) f(X) f(X) 的期望 E p [ f ( X ) ] \mathbb{E}_p[f(X)] Ep[f(X)] 进行估计,并且我们有一些从 p p p 中采样的样本,那么朴素的想法是,直接关于 p p p 采样,把采样到的值加起来求平均
E p [ f ( X ) ] = 1 n ∑ i f i ( X ) \mathbb{E}_p[f(X)] = \frac{1}{n} \sum_{i} f_i(X) Ep[f(X)]=n1i∑fi(X)
但是问题在于,如果采样的样本个数比较少,很可能采样的全都是 0.1,那么和理论值 0.9*0.1+0.1*0.9=0.18 就相差很大。也就是这样的估计方法方差过大。
这个问题的本质原因在于 f ( X ) f(X) f(X)和 p ( X ) p(X) p(X)形状的不匹配:在 f ( X ) f(X) f(X)贡献比较大的值的位置, p ( X ) p(X) p(X)采样的概率很小,一旦采样个数过少, f ( X ) f(X) f(X)不足以产生足够的对 E p [ f ( X ) ] \mathbb{E}_p[f(X)] Ep[f(X)]的贡献,因此产生很大的方差
有什么解决办法呢?
重要性采样
如果我们可以换另一个已知的简单的采样分布 q ( X ) q(X) q(X),使得它和 ∣ p ( X ) f ( X ) ∣ |p(X)f(X)| ∣p(X)f(X)∣匹配,那么方差就能够变小。(这也是此方法命名为重要性采样的原因)
我们可以给积分里面上下乘以一个 q(X),就可以变换成关于 q q q 求另一个表达式的期望
E p [ f ( X ) ] = ∫ X p ( X ) f ( X ) d X = ∫ X q ( X ) p ( X ) q ( X ) f ( X ) d X = E q [ p ( X ) q ( X ) f ( X ) ] \mathbb{E}_p[f(X)] = \int_X p(X)f(X) dX=\int_X q(X) \frac{p(X)}{q(X)}f(X) dX= \mathbb{E}_q[\frac{p(X)}{q(X)}f(X)] Ep[f(X)]=∫Xp(X)f(X)dX=∫Xq(X)q(X)p(X)f(X)dX=Eq[q(X)p(X)f(X)]
由于 p , q , f p,q,f p,q,f 的值我们都是可以计算的,假设 q q q 也可以正常采样,那么这个期望是可以求的。
真的有用?
我们不妨取 q ( X ) q(X) q(X) 和 ∣ p ( X ) f ( X ) ∣ |p(X)f(X)| ∣p(X)f(X)∣ 完美匹配,即 q ( X ) = 0.5 , X = x i , ∀ i q(X) = 0.5, \ \ X=x_i,\ \forall i q(X)=0.5, X=xi, ∀i
然后我们关于 q q q 采样,求 p ( X ) q ( X ) f ( X ) \frac{p(X)}{q(X)}f(X) q(X)p(X)f(X) 的期望
| q ( X ) q(X) q(X) | 0.5 | 0.5 |
|---|---|---|
| p ( X ) q ( X ) f ( X ) \frac{p(X)}{q(X)}f(X) q(X)p(X)f(X) | 0.18 | 0.18 |
好了,你随便从 q q q 采,能和理论值不一样算我输

无论怎么取,我们估计的期望 E ^ q [ p ( X ) q ( X ) f ( X ) ] = 0.18 ∗ 0.5 + 0.18 ∗ 0.5 = 0.18 \mathbb{\hat{E}}_q[\frac{p(X)}{q(X)}f(X)] =0.18 * 0.5 + 0.18 * 0.5 = 0.18 E^q[q(X)p(X)f(X)]=0.18∗0.5+0.18∗0.5=0.18 和理论值完美符合。
重要性采样真的是有用的。不过这只是一个极端的例子,实际上要取这样的一个 q q q 也并不是很容易,还是要到具体领域问题里面具体分析。
相关文章:

【概率方法】重要性采样
从一个极简分布出发 假设我们有一个关于随机变量 X X X 的函数 f ( X ) f(X) f(X),满足如下分布 p ( X ) p(X) p(X)0.90.1 f ( X ) f(X) f(X)0.10.9 如果我们要对 f ( X ) f(X) f(X) 的期望 E p [ f ( X ) ] \mathbb{E}_p[f(X)] Ep[f(X)] 进行估计࿰…...
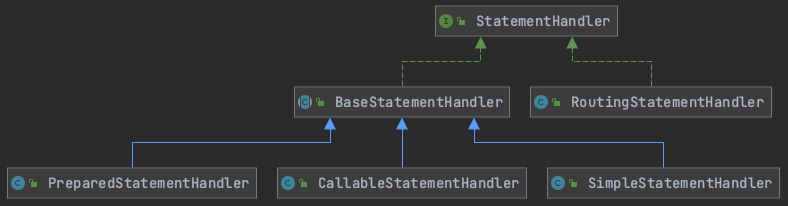
MyBatis 四大核心组件之 StatementHandler 源码解析
🚀 作者主页: 有来技术 🔥 开源项目: youlai-mall 🍃 vue3-element-admin 🍃 youlai-boot 🌺 仓库主页: Gitee 💫 Github 💫 GitCode 💖 欢迎点赞…...

用Guava做本地缓存示例
缓存的作用 提升系统性能,暂时在内存中保存业务系统的数据处理结果,并且等待下次访问使用 本地缓存和分布式缓存 缓存分为本地缓存与分布式缓存。本地缓存为了保证线程安全问题,一般使用ConcurrentMap的方式保存在内存之中,而常…...

Django多对多ManyToManyField字段
Django是一个支持多对多关系的Web框架,可以在模型中定义多对多关系。多对多关系通常涉及两个实体之间的复杂交互,例如用户和组之间的关系,或者课程和学生之间的关系。在Django中,可以使用ManyToManyField字段来定义多对多关系。 …...

docker-centos中基于keepalived+niginx模拟主从热备完整过程
文章目录 一、环境准备二、主机1、环境搭建1.1 镜像拉取1.2 创建网桥1.3 启动容器1.4 配置镜像源1.5 下载工具包1.6 下载keepalived1.7 下载nginx 2、配置2.1 配置keepalived2.2 配置nginx2.2.1 查看nginx.conf2.2.2 修改index.html 3、启动3.1 启动nginx3.2 启动keepalived 4、…...

软件科技成果鉴定测试需提供哪些材料?
为了有效评估科技成果的质量,促进科技理论向实际应用转化,所以需要进行科技成果鉴定测试。申请鉴定的科技成果范围是指列入国家和省、自治区、直辖市以及国务院有关部门科技计划内的应用技术成果,以及少数科技计划外的重大应用技术成果。 …...

办公word-从不是第一页添加页码
总结 实际需要注意的是,分隔符、分节符和分页符并不是一个含义 分隔符包含其他两个;分页符:是增加一页;分节符:指将文档分为几部分。 从不是第一页插入页码1步骤 1,插入默认页码 自己可以测试时通过**…...
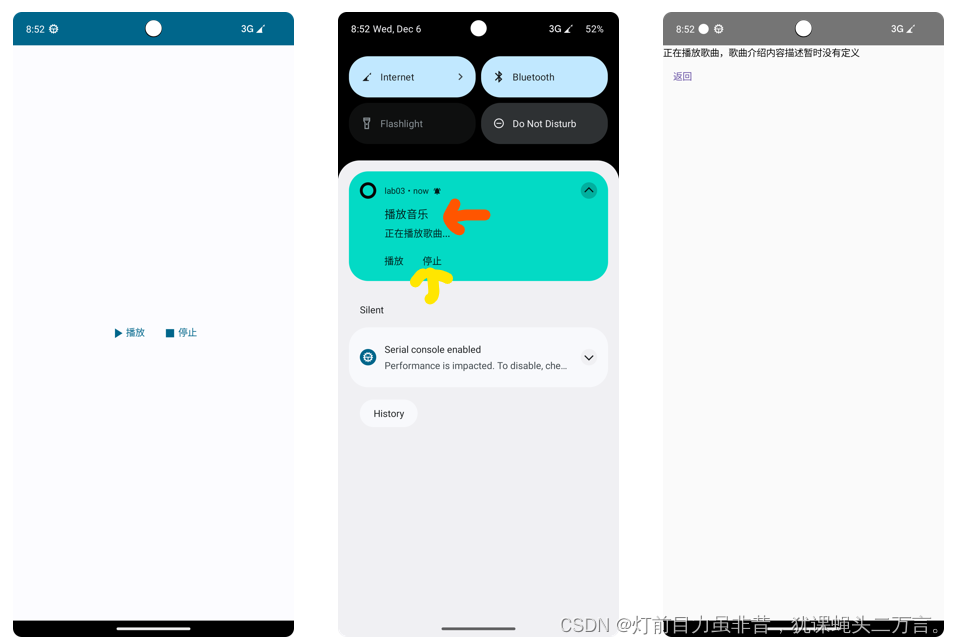
Android笔记(十七):PendingIntent简介
PendingIntent翻译成中文为“待定意图”,这个翻译很好地表示了它的涵义。PendingIntent描述了封装Intent意图以及该意图要执行的目标操作。PendingIntent封装Intent的目标行为的执行是必须满足一定条件,只有条件满足,才会触发意图的目标操作。…...
为 Compose MultiPlatform 添加 C/C++ 支持(2):在 jvm 平台使用 jni 实现桌面端与 C/C++ 互操作
前言 在上篇文章中我们已经介绍了实现 Compose MultiPlatform 对 C/C 互操作的基本思路。 并且先介绍了在 kotlin native 平台使用 cinterop 实现与 C/C 的互操作。 今天这篇文章将补充在 jvm 平台使用 jni。 在 Compose MultiPlatform 中,使用 jvm 平台的是 An…...
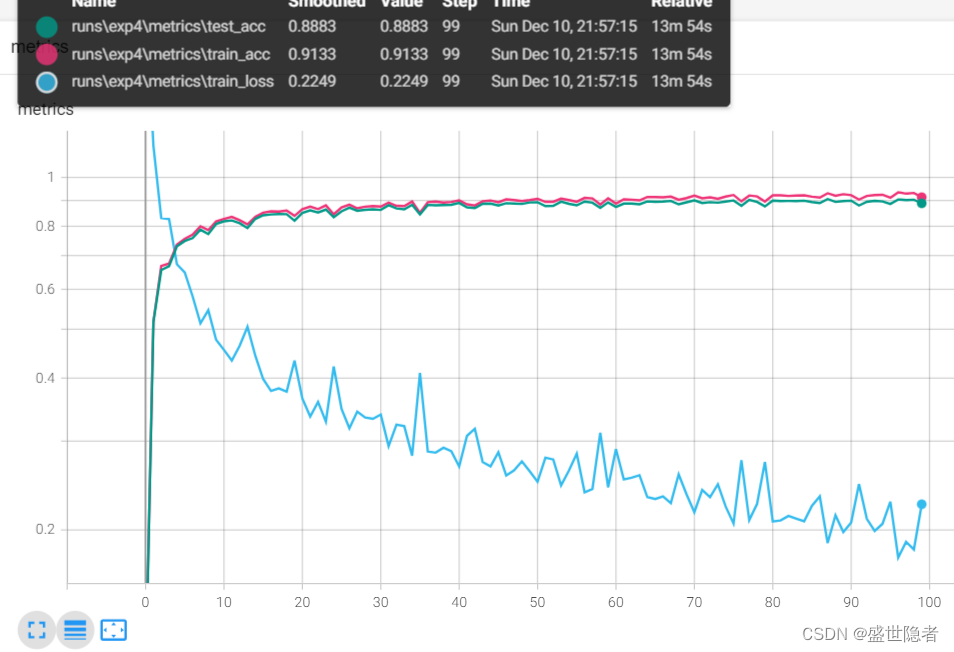
【PyTorch】卷积神经网络
文章目录 1. 理论介绍1.1. 从全连接层到卷积层1.1.1. 背景1.1.2. 从全连接层推导出卷积层 1.2. 卷积层1.2.1. 图像卷积1.2.2. 填充和步幅1.2.3. 多通道 1.3. 池化层(又称汇聚层)1.3.1. 背景1.3.2. 池化运算1.3.3. 填充和步幅1.3.4. 多通道 1.4. 卷积神经…...

qt可以详细写的项目或技术
1.QT 图形视图框架 2.QT 模型视图结构 3.QT列表显示大量信息 4.QT播放器 5.QT 编解码 6.QT opencv...
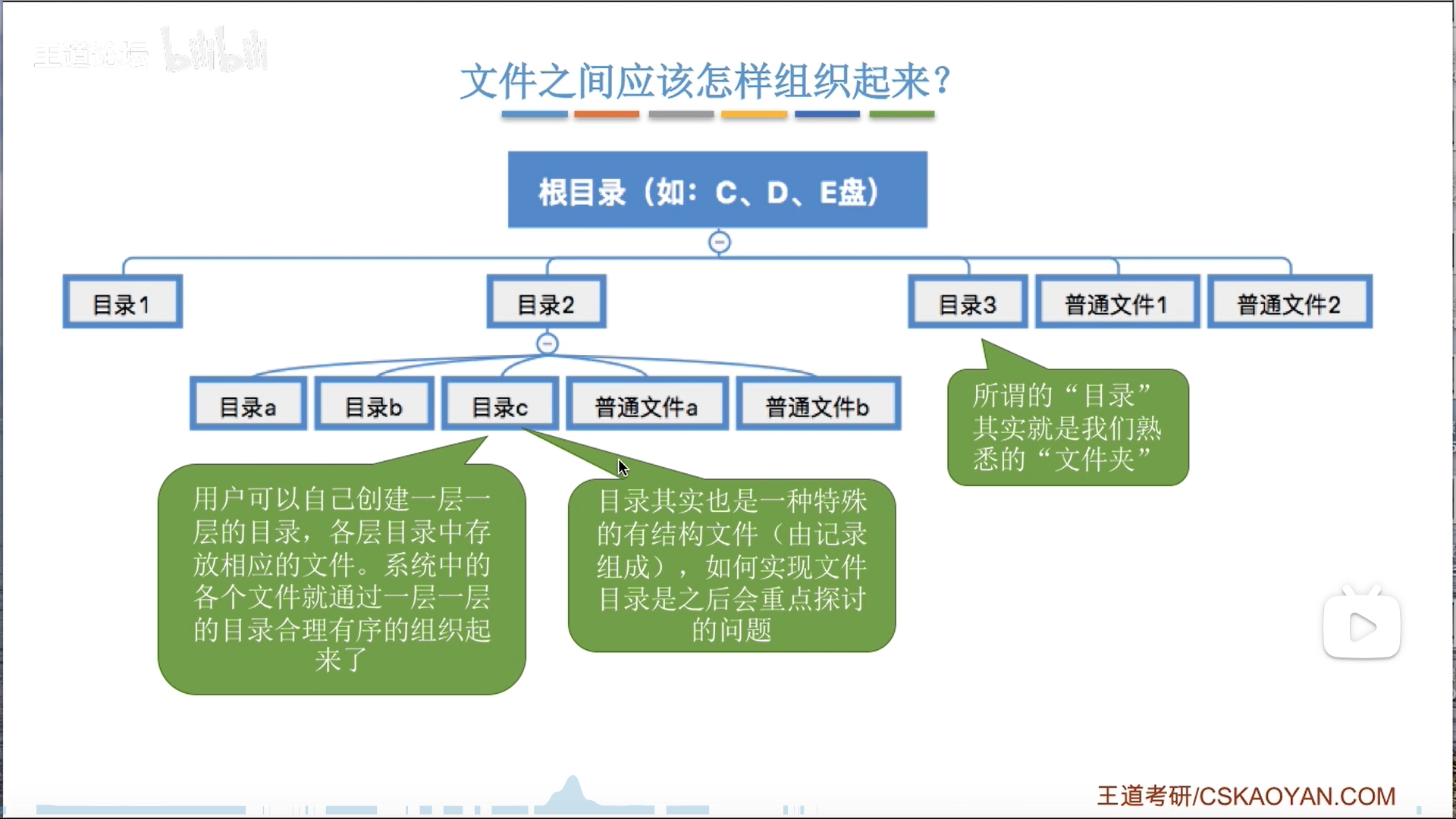
操作系统笔记——储存系统、文件系统(王道408)
文章目录 前言储存系统地址转换内存扩展覆盖交换 储存器分配——连续分配固定大小分区动态分区分配动态分区分配算法 储存器分配——非连续分配页式管理基本思想地址变换硬件快表(TLB)多级页表 段式管理段页式管理 虚拟储存器——基于交换的内存扩充技术…...

基于Html+腾讯云播SDK开发的m3u8播放器
周末业余时间在家无事,学习了一下腾讯的云播放sdk,并制作了一个小demo(m3u8播放器),该在线工具是基于腾讯的云播sdk开发的,云播sdk非常牛,可以支持多种播放格式。 预览地址 m3u8player.org 源码…...

uniapp小程序分享为灰色
引用:https://www.cnblogs.com/panwudi/p/17074172.html uniapp开发的微信小程序,没有转发,分享: 创建一个mixin:common/share.js export default {onShareAppMessage(res) { //发送给朋友return {}},onShareTimeline(res) {//…...
python:五种算法(OOA、WOA、GWO、PSO、GA)求解23个测试函数(python代码)
一、五种算法简介 1、鱼鹰优化算法OOA 2、鲸鱼优化算法WOA 3、灰狼优化算法GWO 4、粒子群优化算法PSO 5、遗传算法GA 二、5种算法求解23个函数 (1)23个函数简介 参考文献: [1] Yao X, Liu Y, Lin G M. Evolutionary programming made…...

DIP——添加运动模糊与滤波
1.运动模糊 为了模拟图像退化的过程,在这里创建了一个用于模拟运动模糊的点扩散函数,具体模糊的方向取决于输入的motion_angle。如果运动方向接近水平,则模糊效果近似水平,如果运动方向接近垂直,则模糊效果近似垂直。具…...
——SQL处理过程)
SQL Server查询计划(Query Plan)——SQL处理过程
6. 查询计划(Query Plan) 6.1. SQL处理过程 就SQL语句的处理过程而言,各关系库间大同小异,尤其是商业库之间实现机制和细节差别更小些,其功能及性能支持方面也更加强大和完善。SQL Server作为商业库中的后起之秀,作为SQL语句处理过程的主要支撑和保障,其优化器及相关机…...

【动手学深度学习】(十二)现代卷积神经网络
文章目录 一、深度卷积神经网络AlexNet1.理论知识 一、深度卷积神经网络AlexNet 1.理论知识 ImageNet(2010) 图片自然物体的彩色图片手写数字的黑色图片大小468 * 38728*28样本数1.2M60K类数100010 AlexNet AlexNet赢了2012ImageNet竞赛更深更大的LeNet主要改进ÿ…...
【小沐学Python】Python实现TTS文本转语音(speech、pyttsx3、百度AI)
文章目录 1、简介2、Windows语音2.1 简介2.2 安装2.3 代码 3、pyttsx33.1 简介3.2 安装3.3 代码 4、ggts4.1 简介4.2 安装4.3 代码 5、SAPI6、SpeechLib7、百度AI8、百度飞桨结语 1、简介 TTS(Text To Speech) 译为从文本到语音,TTS是人工智能AI的一个模组…...

TCP通信
第二十一章 网络通信 本章节主要讲解的是TCP和UDP两种通信方式它们都有着自己的优点和缺点 这两种通讯方式不通的地方就是TCP是一对一通信 UDP是一对多的通信方式 接下来会一一讲解 TCP通信 TCP通信方式呢 主要的通讯方式是一对一的通讯方式,也有着优点和缺点…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

自定义线程池1.2
自定义线程池 1.2 1. 简介 上次我们实现了 1.1 版本,将线程池中的线程数量交给使用者决定,并且将线程的创建延迟到任务提交的时候,在本文中我们将对这个版本进行如下的优化: 在新建线程时交给线程一个任务。让线程在某种情况下…...

react-pdf(pdfjs-dist)如何兼容老浏览器(chrome 49)
之前都是使用react-pdf来渲染pdf文件,这次有个需求是要兼容xp环境,xp上chrome最高支持到49,虽然说iframe或者embed都可以实现预览pdf,但为了后续的定制化需求,还是需要使用js库来渲染。 chrome 49测试环境 能用的测试…...
