排序算法---选择排序
1.实现流程:
1. 把第一个没有排序过的元素设置为最小值;
2. 遍历每个没有排序过的元素;
3. 如果元素 < 现在的最小值;
4. 将此元素设置成为新的最小值;
5. 将最小值和第一个没有排序过的位置交换
选择排序执行流程
2.代码实现
let arr = [17,25,25,28,38,3,43,43,35,45,5]function chooseSort() {let indexMin = 0;// 选择n-1次for (let i=0; i<arr.length-1; i++) {let indexMin = i;for (let j=i+1; j<arr.length; j++) {if (arr[j]<arr[indexMin]) {indexMin = j;}}if (indexMin != i) {let temp = arr[i];arr[i] = arr[indexMin];arr[indexMin] = temp;}}console.log(arr)}chooseSort()运行结果:
3.复杂度分析
1. 时间复杂度:找出执行次数最多的语句即可
if (arr[j]<arr[indexMin]) {indexMin = j;
}基于上述每一趟比较的次数,可以得到总的比较次数,就是这个判断语句执行的次数
=> 当i=0时, 需要比较n-1-0次
当i=1时,需要比较n-1-1次
......
当i=n-3时, 需要比较n-1-(n-3) = 2
当i=n-2时, 需要比较n-1-(n-2) = 1
当i=n-1时, 需要比较n-1-(n-1) = 0
=> (n-1)+(n-2)+(n-3)+...+1+0 = [n(n-1)]/2 = n^2/2 - n/2 + 1/2
=> 去掉系数、低阶和常量
=> 则时间复杂度为 O(n^2)
2. 空间复杂度: 冒泡排序中并没有用到额外的空间,所以空间复杂度为 O(1)
3. 冒泡排序是不稳定的排序算法:从上述的视频可以看出,数组中有两个43,然而在排完序后,原本前面的43跑到了后面
相关文章:

排序算法---选择排序
1.实现流程: 1. 把第一个没有排序过的元素设置为最小值; 2. 遍历每个没有排序过的元素; 3. 如果元素 < 现在的最小值; 4. 将此元素设置成为新的最小值; 5. 将最小值和第一个没有排序过的位置交换 选择排序执行流程…...

物联网IC
物联网IC 电子元器件百科 文章目录 物联网IC前言一、物联网IC是什么二、物联网IC的类别三、物联网IC的应用实例四、物联网IC的作用原理总结前言 物联网IC的功能和特性可以根据不同的物联网应用需求来选择和配置,以满足物联网设备在连接、通信、感知和控制方面的需求。 一、物…...

2022年第十一届数学建模国际赛小美赛A题翼龙如何飞行解题全过程文档及程序
2022年第十一届数学建模国际赛小美赛 A题 翼龙如何飞行 原题再现: 翼龙是翼龙目中一个已灭绝的飞行爬行动物分支。它们存在于中生代的大部分时期:从三叠纪晚期到白垩纪末期。翼龙是已知最早进化出动力飞行的脊椎动物。它们的翅膀是由皮肤、肌肉和其他组…...

Blender学习--制作带骨骼动画的机器人
1. 首先创建一个机器人模型 时间关系,这部分步骤有时间补充 2. 然后为机器人创建一副骨架 时间关系,这部分步骤有时间补充 3.骨骼绑定 切换到物体模式,选中机器人头部,Shift选中骨骼,切换到姿态模式,&am…...

单片机学习13——串口通信
单片机的通信功能: 实现单片机和单片机的信息交换,实现单片机和计算机的信息交换。 计算机通信是指计算机与外部设备或计算机与计算机之间的信息交换。 通信有并行通信和串行通信两种方式。 在多微机系统以及现在测控系统中信息的交换多采用串行通信方…...
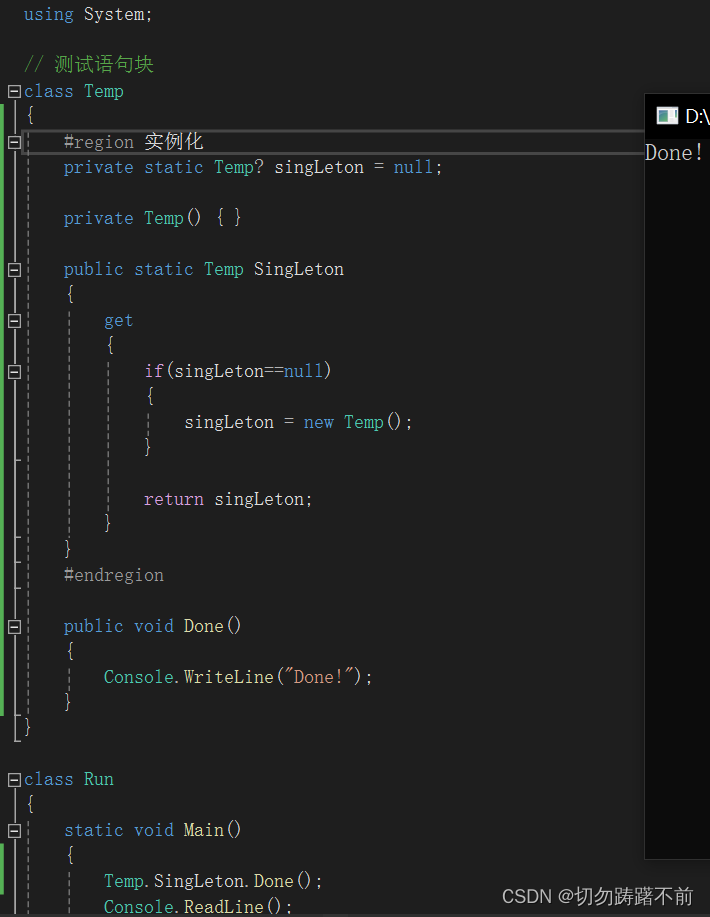
Unity 实现单例模式
目录 基本概念 饿汉模式(推荐) 懒汉模式: 基本概念 单例模式:类只有一个实例,一般使用static来实现单例模式; 比如:有一个Test类,实现了单例,假设这个唯一的实例名为SingTonle,实例在类内被实现并被stat…...

【Android12】Android Framework系列--AMS启动Activity分析
AMS启动Activity分析 通过ActivityManagerService(AMS)提供的方法,可以启动指定的Activity。比如Launcher中点击应用图标后,调用AMS的startActivity函数启动应用。 AMS提供的服务通过IActivityManager.aidl文件定义。 // frameworks/base/core/java/an…...

Hive的几种排序方式、区别,使用场景
一、几种排序和区别 Hive 支持两种主要的排序方式:ORDER BY 和 SORT BY。除此之外,还有 DISTRIBUTE BY 和 CLUSTER BY 语句,它们也在排序和数据分布方面发挥作用。 1. ORDER BY ORDER BY 在 Hive 中用于对查询结果进行全局排序࿰…...
设计模式-外观模式
设计模式专栏 模式介绍模式特点应用场景外观模式和里氏替换原则的区别代码示例Java实现外观模式python实现外观模式 外观模式在spring中的应用 模式介绍 外观模式(Facade Pattern)是一种结构性设计模式,它隐藏了系统的复杂性,并向…...
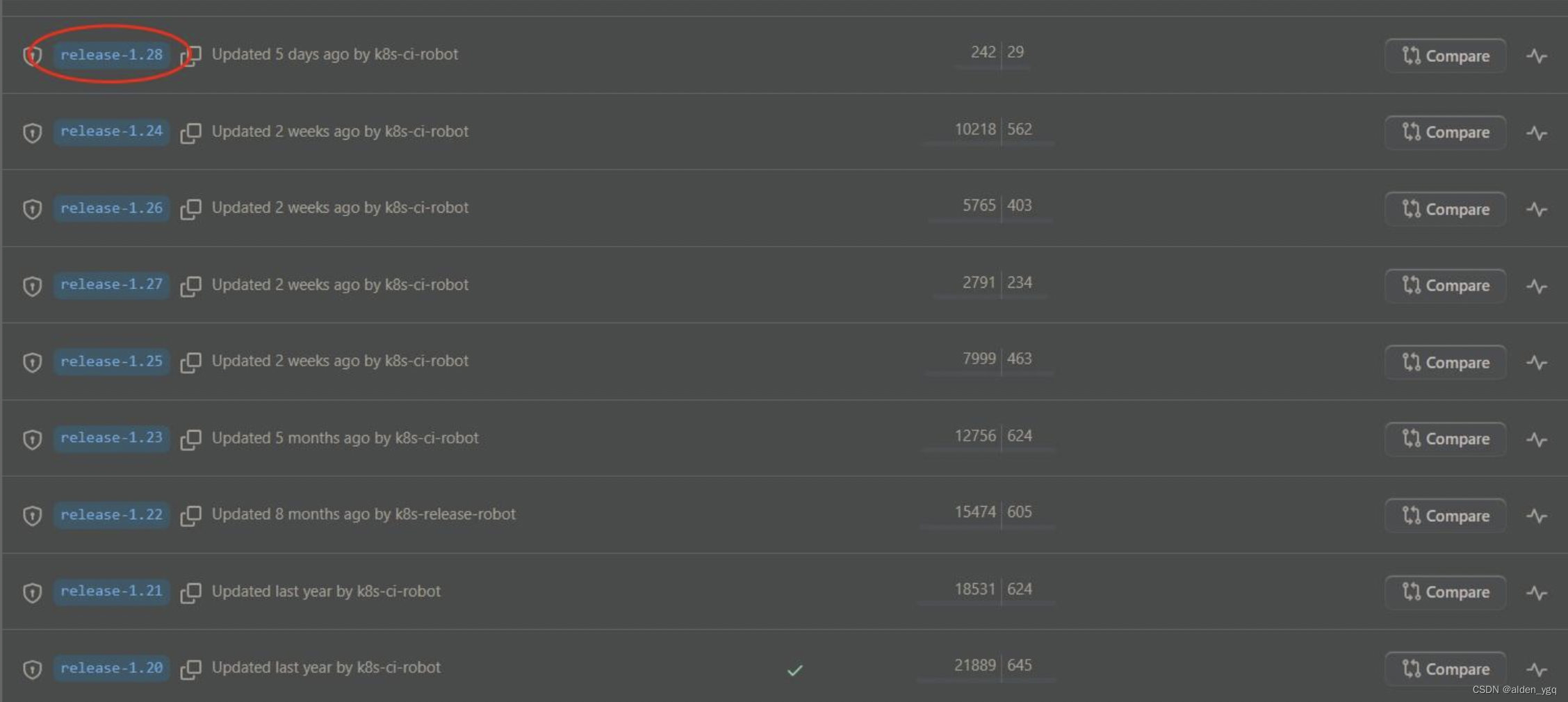
Kubernetes实战(九)-kubeadm安装k8s集群
1 环境准备 1.1 主机信息 iphostname10.220.43.203master10.220.43.204node1 1.2 系统信息 $ cat /etc/redhat-release Alibaba Cloud Linux (Aliyun Linux) release 2.1903 LTS (Hunting Beagle) 2 部署准备 master/与slave主机均需要设置。 2.1 设置主机名 # master h…...
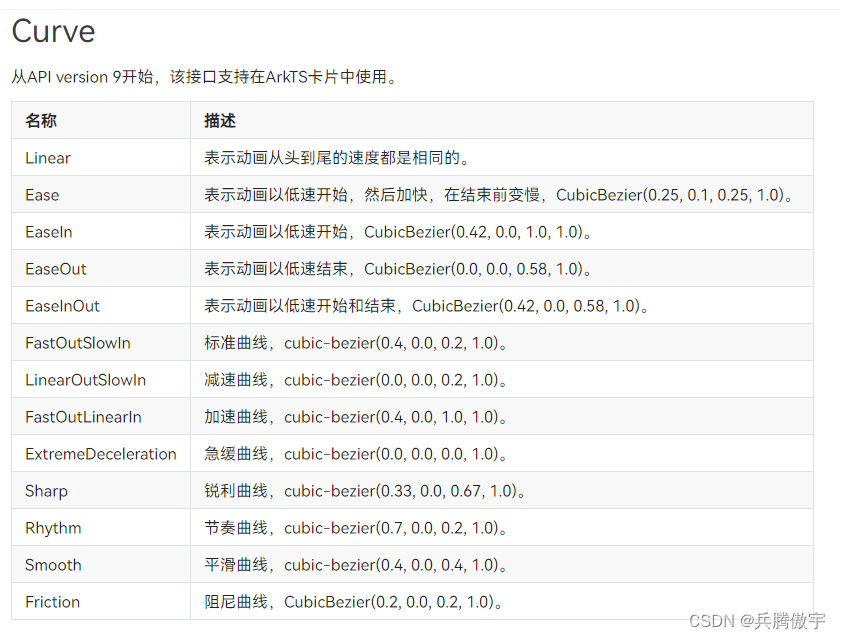
【HarmonyOS开发】拖拽动画的实现
动画的原理是在一个时间段内,多次改变UI外观,由于人眼会产生视觉暂留,所以最终看到的就是一个“连续”的动画。UI的一次改变称为一个动画帧,对应一次屏幕刷新,而决定动画流畅度的一个重要指标就是帧率FPS(F…...

提高问卷填写率的策略与方法
在现代社会的研究中,问卷调研是一种常见的数据收集方式。但是,随着数据的快速传播和竞争激烈的市场环境,怎样吸引大量的人填好问卷成为了科研人员关心的问题。本文将介绍一些方式和策略,以帮助你吸引大量的人填好问卷,…...

软件工程考试复习
第一章、软件工程概述 🌟软件程序数据文档(考点) 🌟计算机程序及其说明程序的各种文档称为 ( 文件 ) 。计算任务的处理对象和处理规则的描述称为 ( 程序 )。有关计算机程序功能、…...
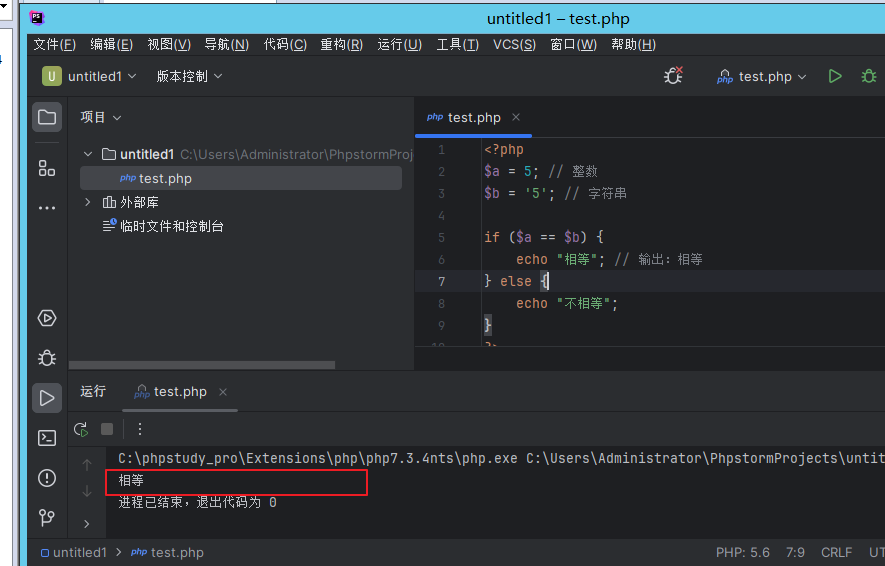
PHP基础 - 类型比较
在 PHP 中,作为一种弱类型语言,它提供了松散比较和严格比较两种方式来比较变量的值和类型。 松散比较: 使用两个等号(==)进行比较,只会比较变量的值,而不会考虑它们的数据类型。例如: $a = 5; // 整数 $b = 5; // 字符串if ($a == $b) {echo "相等"; // 输…...

张正友相机标定法原理与实现
张正友相机标定法是张正友教授1998年提出的单平面棋盘格的相机标定方法。传统标定法的标定板是需要三维的,需要非常精确,这很难制作,而张正友教授提出的方法介于传统标定法和自标定法之间,但克服了传统标定法需要的高精度标定物的缺点,而仅需使用一个打印出来的棋盘格就可…...
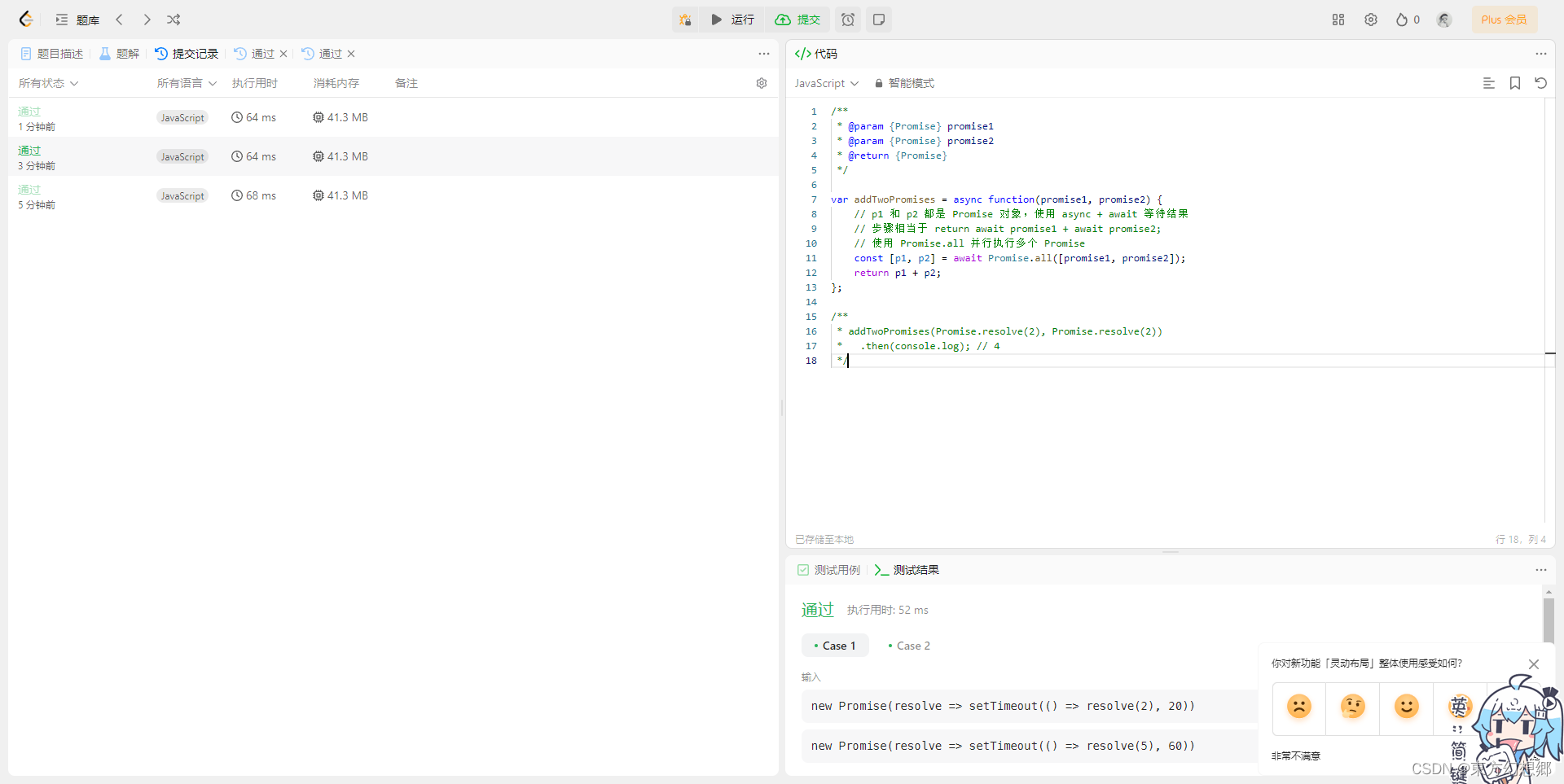
【LeetCode】2723. 两个 Promise 对象相加
两个 Promise 对象相加 题目题解 题目 给定两个 promise 对象 promise1 和 promise2,返回一个新的 promise。promise1 和 promise2 都会被解析为一个数字。返回的 Promise 应该解析为这两个数字的和。 示例 1: 输入: promise1 new Promise…...

设计模式--命令模式的简单例子
引入:以一个对数组的增删改查为例。通过命令模式可以对数组进行增删改查以及撤销回滚。 一、基本概念 命令模式有多种分法,在本文中主要分为CommandMgr、Command、Receiver. CommandMgr主要用于控制命令执行等操作、Command为具体的命令、Receiver为命…...

排序算法之六:快速排序(非递归)
快速排序是非常适合使用递归的,但是同时我们也要掌握非递归的算法 因为操作系统的栈空间很小,如果递归的深度太深,容易造成栈溢出 递归改非递归一般有两种改法: 改循环借助栈(数据结构) 图示算法 不是…...

【概率方法】重要性采样
从一个极简分布出发 假设我们有一个关于随机变量 X X X 的函数 f ( X ) f(X) f(X),满足如下分布 p ( X ) p(X) p(X)0.90.1 f ( X ) f(X) f(X)0.10.9 如果我们要对 f ( X ) f(X) f(X) 的期望 E p [ f ( X ) ] \mathbb{E}_p[f(X)] Ep[f(X)] 进行估计࿰…...
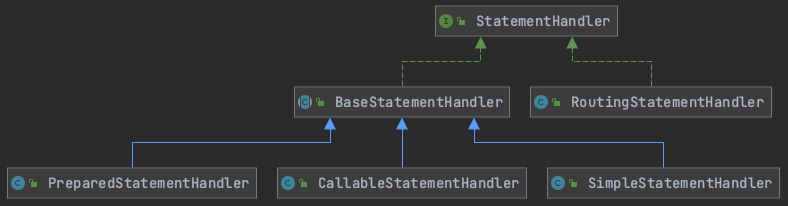
MyBatis 四大核心组件之 StatementHandler 源码解析
🚀 作者主页: 有来技术 🔥 开源项目: youlai-mall 🍃 vue3-element-admin 🍃 youlai-boot 🌺 仓库主页: Gitee 💫 Github 💫 GitCode 💖 欢迎点赞…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...
