当前位置： 首页 > news >正文

Hough算法数学原理

news 2026/2/8 20:36:02

直线的极坐标方程：

x = x 0 + r cos ⁡ θ x= x_0 + r\cos \theta x=x0​+rcosθ

y = y 0 + r sin ⁡ θ y= y_0 + r\sin \theta y=y0​+rsinθ

x cos ⁡ θ = x 0 cos ⁡ θ + r cos ⁡ 2 θ x \cos \theta =x_0 \cos \theta + r \cos^2 \theta xcosθ=x0​cosθ+rcos2θ

y sin ⁡ θ = y 0 sin ⁡ θ + r sin ⁡ 2 θ y \sin \theta =y_0 \sin \theta + r \sin^2 \theta ysinθ=y0​sinθ+rsin2θ

x cos ⁡ θ + y sin ⁡ θ = x 0 cos ⁡ θ + y 0 sin ⁡ θ + r x \cos\theta + y \sin \theta =x_0 \cos \theta + y_0 \sin \theta + r xcosθ+ysinθ=x0​cosθ+y0​sinθ+r

若 x 0 = 0 , y 0 = 0 , 则 ： x_0 =0,y_0 = 0,则： x0​=0,y0​=0,则：
x cos ⁡ θ + y sin ⁡ θ = r x \cos\theta + y \sin \theta = r xcosθ+ysinθ=r

参考链接：https://zhuanlan.zhihu.com/p/106099760

相关文章：

Hough算法数学原理

直线的极坐标方程： x x 0 r cos ⁡ θ x x_0 r\cos \theta xx0​rcosθ y y 0 r sin ⁡ θ y y_0 r\sin \theta yy0​rsinθ x cos ⁡ θ x 0 cos ⁡ θ r cos ⁡ 2 θ x \cos \theta x_0 \cos \theta r \cos^2 \theta xcosθx0​cosθrcos2θ y sin ⁡ θ…...

编程日记 2023/12/11 18:11:21

基于Debain安装 Docker 和 Docker Compose

一、安装Docker # 先升级一下系统 (Ubuntu / Debian 系) sudo apt-get update sudo apt-get upgrade# 如果你是 CentOS、红帽系列则使用： yum update yum upgrade# 安装 Docker curl -fsSL https://get.docker.com -o get-docker.sh sudo sh get-docker.sh二、Dock…...

编程日记 2023/12/11 18:10:20

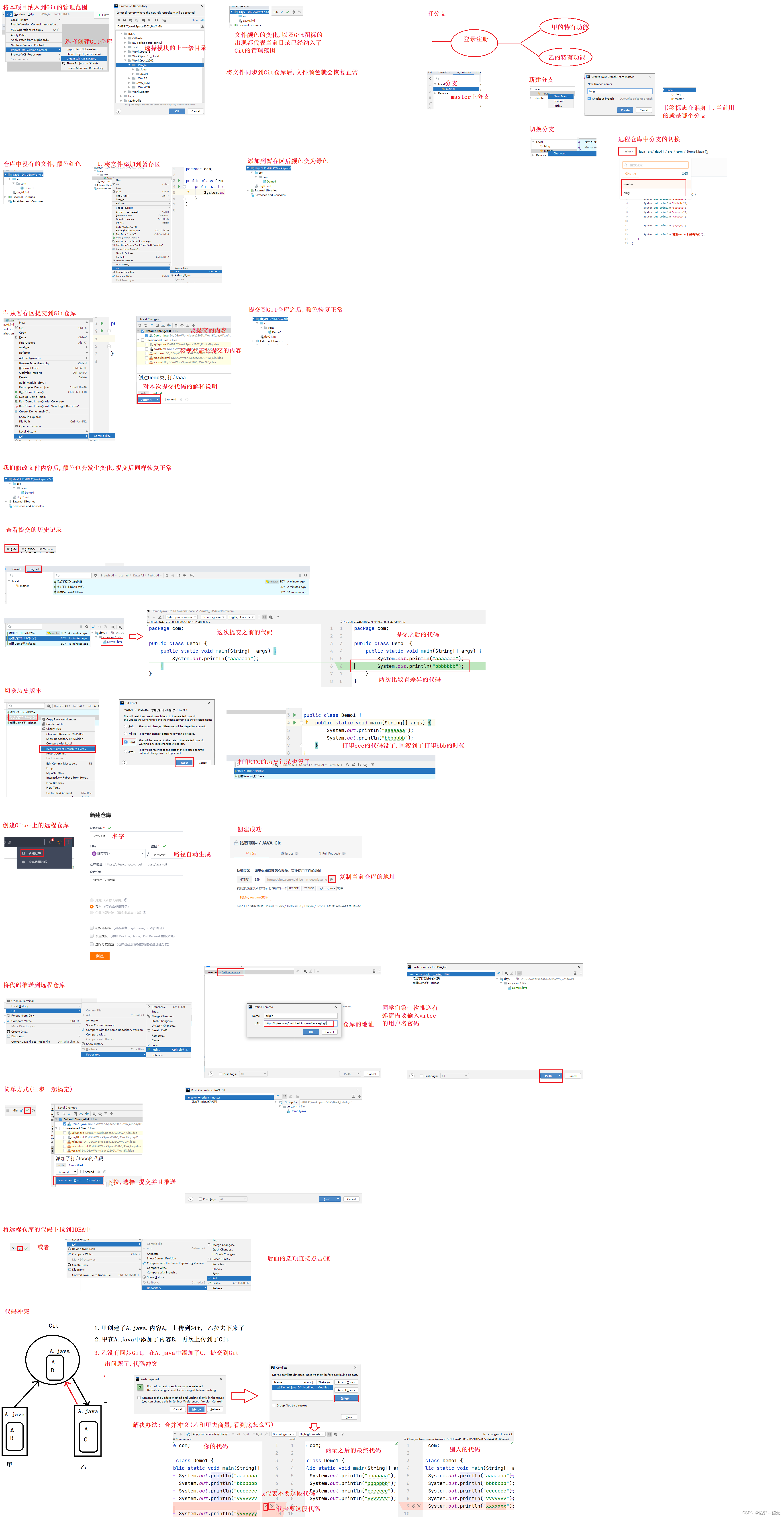
gittee使用教学

一、git简介 Git是一个开源的分布式版本控制系统，用于敏捷高效的处理任何大小项目的版本管理。 核心功能： 项目的版本管理 团队协同开发 二、准备工作 1、下载 Git 2、除了选择安装位置以外，其他都无脑安装 3、检查一下安装情况 win…...

编程日记 2023/12/11 18:09:20

q2-qt-多线程

是的，Qt框架中提供了专门用于线程池的API。Qt的线程池API位于QtConcurrent命名空间下，以及QThreadPool类中。 QtConcurrent命名空间提供了一些高级的API，可以方便地使用线程池来执行并行任务。其中，QtConcurrent::run()函数可以用…...

编程日记 2023/12/11 18:07:18

指针,函数指针，二级指针，指针传参，回调函数，指针步长

文章目录 指针是什么？指针的定义指针的大小 指针类型指针有哪些类型？指针类型有什么意义？代码演示：(偏移)代码演示(指针解引用时取出的字节数)其他例子 野指针野指针的成因如何避免野指针 指针运算指针整数指针-指针指针的关系运算…...

编程日记 2023/12/11 18:06:16

StringUtils.isEmpty()方法过期的替代方法

1、问题概述？ 今天在准备使用StringUtils.isEmpty()工具判断字符串是否为空的时候，突然发现idEmpty上出现了横线，这就表示这个方法可以实现但是已经过期了，官方不推荐使用了。 原因其实是因为有人给官方提交了一个问题&#xff…...

编程日记 2023/12/11 18:05:15

智慧电力运维综合辅助监控系统

智慧电力运维综合辅助监控系统是一种基于现代信息技术的电力运维管理工具，旨在提高电力运行安全，降低运维成本，提高服务质量。依托电易云-智慧电力物联网，该系统通过多种传感器和现场监测装置，远程在线监测、监视电力设…...

编程日记 2023/12/11 18:01:13

v-model和:model的区别

问题 在我们使用Element plus框架时&#xff0c;经常会遇到表单&#xff0c;比如代码块&#xff1a; <el-form ref"ruleFormRef" :model"ruleForm" :rules"rules" label-width"120px" class"demo-ruleForm" :size"…...

编程日记 2023/12/11 18:00:12

网络攻击（二）--情报搜集阶段

4.1. 概述 在情报收集阶段&#xff0c;你需要采用各种可能的方法来收集将要攻击的客户组织的所有信息&#xff0c;包括使用社交网络、Google Hacking技术、目标系统踩点等等。 而作为渗透测试者&#xff0c;你最为重要的一项技能就是对目标系统的探查能力&#xff0c;包括获知…...

编程日记 2023/12/11 17:59:11

oracle异常：ORA-03297:文件包含在请求的 RESIZE 值以外使用的数据

出现这个问题&#xff0c;主要是在对表空间扩容的时候&#xff0c;扩容的大小<实际数据文件大小 1、扩容的语句 alter database datafile D:\APP\ADMINISTRATOR\ORADATA\ORCL\USER.DBF resize 2G; 2、若何确定扩容大小是否比实际文件大 根据路径找到文件&#xff0c;查看…...

编程日记 2023/12/11 17:57:09

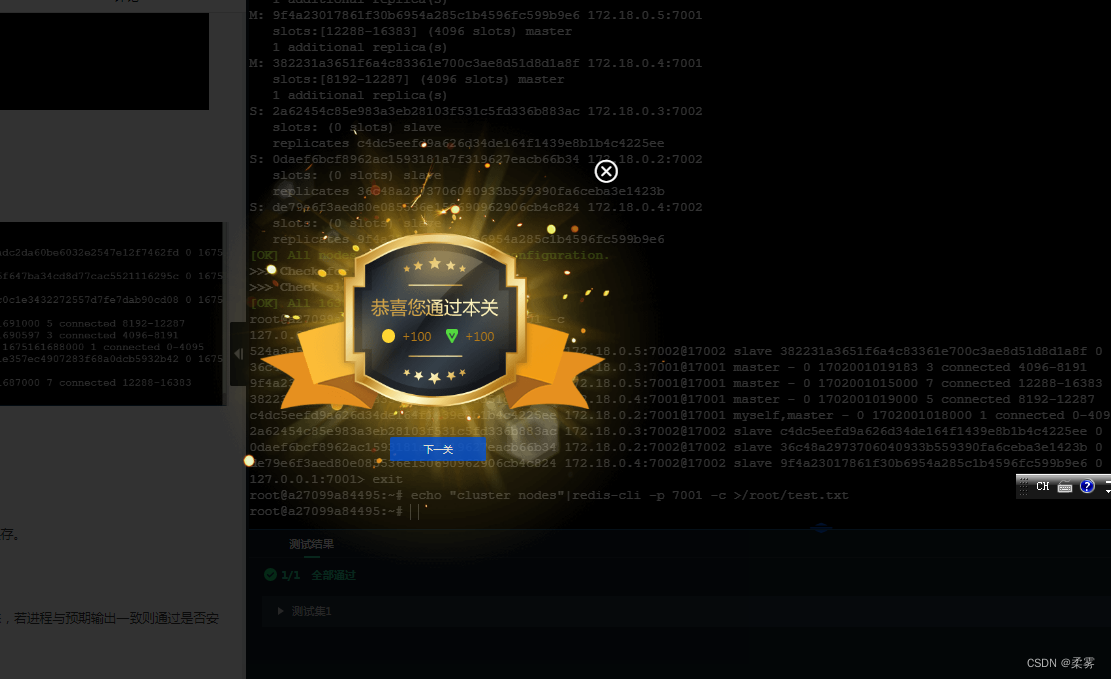
Redis 环境搭建

文章目录 第1关&#xff1a;Redis 环境搭建 第1关&#xff1a;Redis 环境搭建 编程要求 根据上述相关知识&#xff0c;在右侧命令行中完成 Redis 集群的部署与安装。 安装完成后&#xff0c;使用 echo “cluster nodes”|redis-cli -p 7001 -c >/root/test.txt 将结果保存。…...

编程日记 2023/12/11 17:55:07

什么是Helpdesk？对工程师有什么帮助？

信息技术时代已然到来&#xff0c;很多IT工程师甚至对Helpdesk都不了解&#xff0c;而Helpdesk已成为许多企业的重要组成部分。那么&#xff0c;什么是Helpdesk呢&#xff1f; Helpdesk&#xff0c;也称为技术支持服务&#xff0c;是一种为用户提供技术帮助和问题解决的服务。它…...

编程日记 2023/12/11 17:53:05

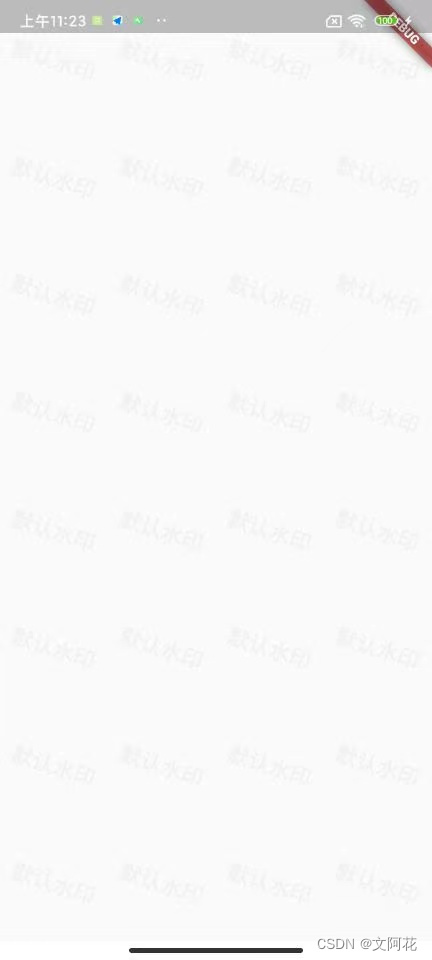
flutter添加全局水印

效果&#xff1a; 可以直接引用&#xff1a;disable_screenshots: ^0.2.0 但是有时候直接引用会报错&#xff0c;可以不引用插件直接把下面的源码工具类放在项目里面 工具类源码&#xff1a; import dart:io; import dart:math;import package:flutter/cupertino.dart; impor…...

编程日记 2023/12/11 17:48:01

Usergolang 一些优质关于sip协议包

在Go语言中&#xff0c;有一些优质的SIP协议包&#xff0c;适用于构建SIP客户端和服务器。以下是其中一些常用的SIP库&#xff1a; 1. github.com/cloudwebrtc/sip - GitHub 地址&#xff1a;[cloudwebrtc/sip](https://github.com/cloudwebrtc/sip) - 该库提供了用于构…...

编程日记 2023/12/11 17:47:00

MYSQL数据类型详解

MySQL支持多种数据类型&#xff0c;这些数据类型可以分为三大类&#xff1a;数值、日期和时间以及字符串&#xff08;字符&#xff09;类型。这些数据类型可以帮助我们根据需要选择合适的类型来存储数据。选择合适的数据类型对于确保数据的完整性和性能至关重要。 以下…...

编程日记 2023/12/11 17:45:58

解决vue3 动态引入报错问题

之前这样写的&#xff0c;能使用&#xff0c;但是有警告 警告&#xff0c;查了下&#xff0c;是动态引入的问题&#xff0c;看到说要用glob 然后再我的基础上&#xff0c;稍微 改了下&#xff0c;就可以了&#xff1a; 最后打印了下&#xff0c;modules[../../components/flowc…...

编程日记 2023/12/11 17:44:57

Mysql dumpling 导入导出sql文件

一&#xff1a;导出命令 mysqldump -u root -p saishi > saishi.sql mysqldump -u root -p saishi > saishi.sql root是用户名 saishi是数据库名 saishi.sql导出文件名 二&#xff1a;选择导入的数据库 cd到安装mysql的文件下&#xff08;找不到可以用&#xff1a;wh…...

编程日记 2023/12/11 17:43:57

【数字经济】你必须知道的SABOE数字化转型

【文末送书】今天推荐一本企业管理类前沿书籍《企业架构驱动数字化转型&#xff1a;以架构为中心的端到端转型方法论》 目录 01传统企业数字化转型面临诸多挑战02SABOE数字化转型五环法为企业转型破除迷雾03文末送书 01传统企业数字化转型面临诸多挑战 即将过去的2023年&#…...

编程日记 2023/12/11 17:42:55

【Python网络爬虫入门教程2】成为“Spider Man”的第二课：观察目标网站、代码编写

Python 网络爬虫入门&#xff1a;Spider man的第二课 写在最前面观察目标网站代码编写 第二课总结 写在最前面 有位粉丝希望学习网络爬虫的实战技巧&#xff0c;想尝试搭建自己的爬虫环境&#xff0c;从网上抓取数据。 前面有写一篇博客分享&#xff0c;但是内容感觉太浅显了…...

编程日记 2023/12/11 17:35:49

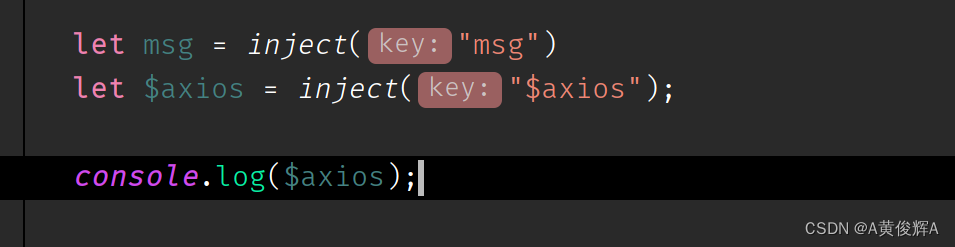
vue2和vue3中注意全局属性的区别（例如全局使用axios ）

vue2中注册一个全局属性 在vue2中注册全局属性是很方便的&#xff0c; 只需要使用 vue.prototype.XXXX XXXX就可以了&#xff0c;如下面的代码 import { Dialog,Notify,Toast } from vant; Vue.prototype.$dialog Dialog Vue.prototype.$notify Notify Vue.prototype.$toa…...

编程日记 2023/12/11 17:30:43

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)

题目&#xff1a;3442. 奇偶频次间的最大差值 I 思路 &#xff1a;哈希&#xff0c;时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况&#xff0c;哈希表这里用数组即可实现。 C版本&#xff1a; class Solution { public:int maxDifference(string s) {int a[26]…...

编程新知 2026/2/7 23:18:31

从深圳崛起的“机器之眼”：赴港乐动机器人的万亿赛道赶考路

进入2025年以来&#xff0c;尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断&#xff0c;但全球市场热度依然高涨&#xff0c;入局者持续增加。 以国内市场为例&#xff0c;天眼查专业版数据显示&#xff0c;截至5月底&#xff0c;我国现存在业、存续状态的机器人相关企…...

编程新知 2026/2/8 7:23:45

Cloudflare 从 Nginx 到 Pingora：性能、效率与安全的全面升级

在互联网的快速发展中&#xff0c;高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司&#xff0c;近期做出了一个重大技术决策&#xff1a;弃用长期使用的 Nginx&#xff0c;转而采用其内部开发…...

编程新知 2026/1/29 21:20:51

[Java恶补day16] 238.除自身以外数组的乘积

给你一个整数数组 nums&#xff0c;返回 数组 answer &#xff0c;其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法&#xff0c;且在 O(n) 时间复杂度…...

编程新知 2025/10/3 13:53:38

Java面试专项一-准备篇

一、企业简历筛选规则 一般企业的简历筛选流程&#xff1a;首先由HR先筛选一部分简历后&#xff0c;在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如&#xff1a;Boss直聘&#xff08;招聘方平台&#xff09; 直接按照条件进行筛选 例如&#xff1a…...

编程新知 2026/1/26 19:10:48

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台

🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型（LLM）的广泛应用，开发者常面临多个挑战： 各大模型（OpenAI、Claude、Gemini、Ollama）接口风格不统一；缺乏一个统一平台进行模型调用与测试；本地模型 Ollama 的集成与前…...

编程新知 2026/1/25 3:31:07

如何更改默认 Crontab 编辑器 ？

在 Linux 领域中&#xff0c;crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用&#xff0c;用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益&#xff0c;允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

编程新知 2026/1/30 3:27:35

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师（题目+回答）

安全领域各种资源&#xff0c;学习文档&#xff0c;以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具&#xff0c;欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

编程新知 2026/1/27 2:41:27

day36-多路IO复用

一、基本概念 &#xff08;服务器多客户端模型&#xff09; 定义&#xff1a;单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用&#xff1a;应用程序通常需要处理来自多条事件流中的事件&#xff0c;比如我现在用的电脑&#xff0c;需要同时处理键盘鼠标…...

编程新知 2026/1/31 7:42:50

windows系统MySQL安装文档

概览&#xff1a;本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容&#xff0c;为学习者提供全面的操作指导。关键要点包括&#xff1a; 解压 &#xff1a;下载完成后解压压缩包&#xff0c;得到MySQL 8.…...

编程新知 2026/2/6 10:22:29