基础算法(1):排序(1):选择排序
今天对算法产生了兴趣,开始学习基础算法,比如排序,模拟,贪心,递推等内容,算法是很重要的,它是解决某个问题的特定方法,程序=数据结构+算法,所以对算法的学习是至关重要的,它可以提高程序效率,不同的算法也是有优劣的,如何进行评价,这也是我们需要知道的,我会在学习中穿插这种评价方法,下面让我们看看第一个基础算法排序中的选择排序。
1.选择排序的实现
选择排序(SelectionSort)算法的工作原理是每一次遍历从待排序的元素中选出最小(或最大)的一个元素,将其放在已经排好序的数列之后,直到全部排好序为止。
其核心就是选择和交换,流程如下:
假如给定初始数据 8 4 2 7 3(红色为每次遍历交换的数据)
第一次排序 2 4 8 7 3
第二次排序 2 3 8 7 4
第三次排序 2 3 4 7 8
首先在未排序序列中找到最小(或最大)元素,放到排序序列的起始位置,然后再从剩余未排序元素中继续寻找最小(或最大)元素,然后放到已排序序列的末尾,直到所有元素全部排好序。
逻辑是这样:
(1)第一轮从下标为 1 到下标为 n-1 的元素中选取最小值,若小于第一个数,则交换
(2)第二轮从下标为 2 到下标为 n-1 的元素中选取最小值,若小于第二个数,则交换
依次类推下去……
我们可以再看一个动画演示加深对过程的理解,本图非本人所作,借鉴别人的。

下面是代码实现:
void selectionSort(int arr[],int len)
{int i,j,min,temp;for(i=0;i<len-1;i++){min=i;//先定义一个最小值对应的下标for(j=i+1;j<len;j++){if(arr[min]>arr[j])//如果大于就更新最小值对应的下标{min=j;}}temp=arr[min];//循环结束,找到本次待排序序列的最小值,和序列首元素进行交换,之后进入下一次循环arr[min]=arr[i];arr[i]=temp;}
}或者下面这个版本
void selectSort(int arr[], int n) {if(n==0||n==1)return;int i, j, minIndex;for (int i = 0; i < n - 1; i++) {minIndex = i;//先定义最小值对应的下标for (int j = i + 1; j < n-1; j++){minIndex = arr[j] < arr[minIndex] ? j : minIndex;//如果小于就更新最小值下标}int temp=arr[min];//循环结束,找到本次待排序序列的最小值,和序列首元素进行交换,之后进入下一次循环arr[min]=arr[i];arr[i]=temp;}
}2.选择排序的时间复杂度
时间复杂度?这是什么玩意?别搞我啊?可能大家在看到这个词的心理状态是这样的,但你先别急。
2.1 时间复杂度
时间复杂度是用来评价算法性能的,它是用来方便开发者估算程序的运行时间,我们如何估计程序运行时间呢?我们通常会估计算法的操作单元数量,来代表程序消耗的时间
假设算法道德问题规模为n,那么操作单元数量就用函数f(n)来表示,随着n的增大,算法执行时间的增长率和f(n)的增长率相同,这就称作算法的时间复杂度,记为O(f(n))。
大O用来表示上界的,当用它作为算法的最坏情况运行时间的上界,就是对任意数据输入的运行时间的上界。
2.2 如何描述时间复杂度

决定使用哪个算法不仅仅要考虑时间复杂度,不是时间复杂越低的越好,要考虑数据规模,如果数据规模很小,甚至可以用O(n^2)的算法比 O(n)的更合适,就像上图中图中 O(5n^2) 和O(100n) 在n小于2的时候 O(5n^2)是更优的,所花费的时间也是最少的。
那我们为什么在计算时间复杂度的时候要忽略常数项系数呢,也就说O(100n) 就是O(n)的时间复杂度,并且要默认O(n) 优于O(n^2) 呢 ?
因为大O其实就是数据量级突破一个点且数据量级非常大的情况下所表现出的时间复杂度,也就是刚才说的上界,在这个时候,常数项系数已经不起决定性作用了,所以可以省略。
例如上图中 20 就是那个点 ,n只要大于20 常数项系数已经不起决定性作用了,其实也包括除最高次数项的其他项。
所以我们说的时间复杂度都是省略常数项系数的,是因为一般情况下我们都是默认数据规模足够的大,基于这样的事实 我们给出的算法时间复杂的的一个排行如下所示:
O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n)
这里只是大概列出概念,后面会专门写一篇来讲这方面的问题。
2.3 选择排序的时间复杂度
从上面的代码我们可以知道选择排序套用了两个循环:
for(i=0;i<n-1;i++)
{for(j=i+1;j<n;j++){}}很显然问题规模是n,问题规模就是需要解决问题处理数据量的大小,显然是处理n个元素的排序问题,规模为n。
当i=0时,下面内循环比较n-1次,每次i+1下面内循环比较n-i次,因此总共循环次数(操作单元数量)为(n-1)+(n-2)+......+2+1=n^2/2,舍去最高项系数,时间复杂度为O(n^2)。
3.leetcode题目
3.1 颜色分类

void sortColors(int* nums, int numsSize) {int i,j,min,temp;for(i=0;i<numsSize-1;i++){min=i;for(j=i+1;j<numsSize;j++){if(nums[min]>nums[j]){min=j;}}temp=nums[min];nums[min]=nums[i];nums[i]=temp;}
}这个没什么好说的,就是排序,太水了,模板题。
3.2 至少是其他数字两倍的最大数

int dominantIndex(int* nums, int numsSize) {if(numsSize==1)return 0;int max=0;for(int i=0;i<numsSize;i++){if(nums[max]<nums[i])max=i;}int minindex=0;for(int i=0;i<numsSize-1;i++){minindex=i;for(int j=i+1;j<numsSize;j++){minindex=nums[j]<nums[minindex]?j:minindex;}if(i!=minindex){int temp=nums[i];nums[i]=nums[minindex];nums[minindex]=temp;}}if(nums[numsSize-1]>=2*nums[numsSize-2])return max;else return -1;
}这个题也不难,关键在于我们要先记录最大数对应的下标,因为我们排序后会破坏原来的顺序,再就是我们只需要判断排序后最后一个数是不是至少是前一个数的两倍,如果这个满足,那这个最大数也必然是其他是的至少两倍。
3.3 判断能否形成等差数列

bool canMakeArithmeticProgression(int* arr, int arrSize) {for(int i=0;i<n;i++){int minindex=i;for(int j=i+1;j<n;j++){minindex=nums[j]<nums[minindex]?j:minindex;}int temp=nums[i];nums[i]=nums[minindex];nums[minindex]=temp;}int d=arr[1]-arr[0];for(int i=2;i<arrSize;i++){if((arr[i]-arr[i-1])!=d)return false;}return true;
}这个题就是先排序,这样我们就可以很容易的判断,先假定公差为前两个数之差,如果遍历后面相邻两个数之差等于该公差,那说明是等差数列,否则不是。
相关文章:

基础算法(1):排序(1):选择排序
今天对算法产生了兴趣,开始学习基础算法,比如排序,模拟,贪心,递推等内容,算法是很重要的,它是解决某个问题的特定方法,程序数据结构算法,所以对算法的学习是至关重要的&a…...
GeoTrust OV证书
当谈到网站安全性和可信度时,GeoTrust OV证书是一个备受推崇的选择。作为一家备受尊敬的数字证书颁发机构,GeoTrust以其卓越的品牌声誉和高质量的产品而闻名于世。GeoTrust OV证书提供了一系列的安全功能,同时还具有出色的性价比,…...
第一个“hello Android”程序
1、首先安装Android studio(跳过) Android Studio是由Google推出的官方集成开发环境(IDE),专门用于Android应用程序的开发。它是基于JetBrains的IntelliJ IDEA IDE构建的,提供了丰富的功能和工具࿰…...
docker-compose安装nacos和msql
docker-compose安装nacos和msql 前言前提已经安装docker-compose,如果没有安装,则可以查看上面系列文章中的安装教程。并且文章中使用的是mobaxterm连接虚拟机。 1、下载2、创建并运行 前言 前提已经安装docker-compose,如果没有安装&#x…...
AnythingLLM:基于RAG方案构专属私有知识库(开源|高效|可定制)
一、前言 继OpenAI和Google的产品发布会之后,大模型的能力进化速度之快令人惊叹,然而,对于很多个人和企业而言,为了数据安全不得不考虑私有化部署方案,从GPT-4发布以来,国内外的大模型就拉开了很明显的差距…...

常见的工作流编排引擎
常见工作流框架:微服务编排引擎 工作流框架还是比较多的,按照语言分类的话,有 Java: jBPM、Activiti、SWF PHP: Tpflow、PHPworkflow Go: Cadence(Cadence由Uber开发并开源,Maxim Fateev是Cadence的主架构师&#…...
)
期末总复习(重点!!!)
一、第6章异常处理 1、什么是异常、什么是异常处理异常是指程序在运行过程中发生的错误事件,影响程序的正常执行。异常并不是一定会发生,默认情况下,程序运行中遇到异常时将会终止,并在控制台打印出异常出现的堆栈信息。异常处理…...

input 获取焦点后样式的修改
一、实现目标 1.没有获取焦点时样子 2.获取焦点时 代码: <input class"input"placeholder"请输入关键字" input"loadNode" />css .input {border-radius: 14px;border:1px solid #e4e4e4;margin: 5px;margin-top: 10px;wi…...
持续集成交付CICD:Jenkins使用GitLab共享库实现自动上传前后端项目Nexus制品
目录 一、实验 1.GitLab本地导入前后端项目 2.Jenkins新建前后端项目流水线 3.Sonarqube录入质量阈与质量配置 4.修改GitLab共享库代码 5.Jenkins手动构建前后端项目流水线 6.Nexus查看制品上传情况 7.优化代码获取RELEASE分支 8.优化Jenkins流水线项目名称 一、实验 …...
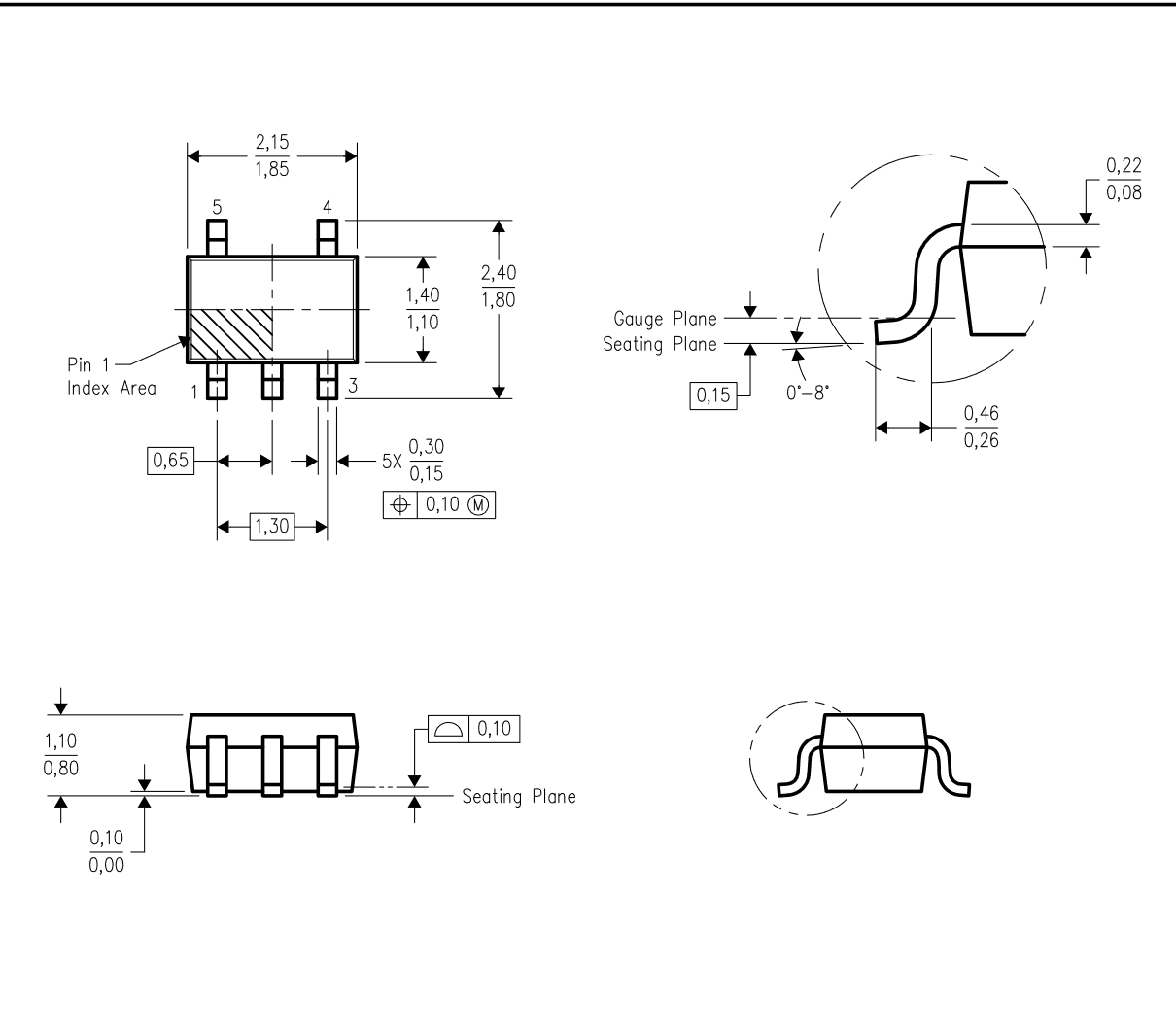
50mA、24V、超低 IQ、低压降稳压器
一、Description The TPS715 low-dropout (LDO) voltage regulators offer the benefits of high input voltage, low-dropout voltage, low-power operation, and miniaturized packaging. The devices, which operate over an input range of 2.5 V to 24 V, are stable wit…...

【Python测试开发】文件上传操作
先写一个上传页面 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>文件上传</title><link href"http://dcn.bootcss/bootstrap/3.3.0/css/bootstrap.min.css" rel"styleshee…...

深兰科技AI医疗健康产品获3000台采购订单
12月6日,武汉某企业与深兰科技签署协议,一次性采购3,000台深兰科技AI生理健康检测仪——扁鹊。 深兰科技AI生理健康检测仪——扁鹊是深兰科技推出的人体生理指标检测产品。基于AI生物技术、融合互联网医疗及AIoT技术,深兰科技AI生理健康检测仪…...

金鸣表格文字识别的图片转word,模块不同,效果有何差异?
金鸣表格文字识别系统可以将图片等格式的文件转为word,而且有好几种输出word的方式,那么,它们都有什么区别呢? 一、表格识别模块输出的word。可以输出文本和表格混合格式的word,比较适合有表格样式的图片转换识别&…...
Qt Creator设置IDE的字体、颜色、主题样式
Qt是一款开源的、跨平台的C开发框架,支持Windows、Linux、Mac系统,从1995发布第一版以来,发展迅猛,最开始是用于Nokia手机的Symbian(塞班)系统和应用程序开发,现在是用于嵌入式软件、桌面软件(比如WPS、VirtualBox)、A…...
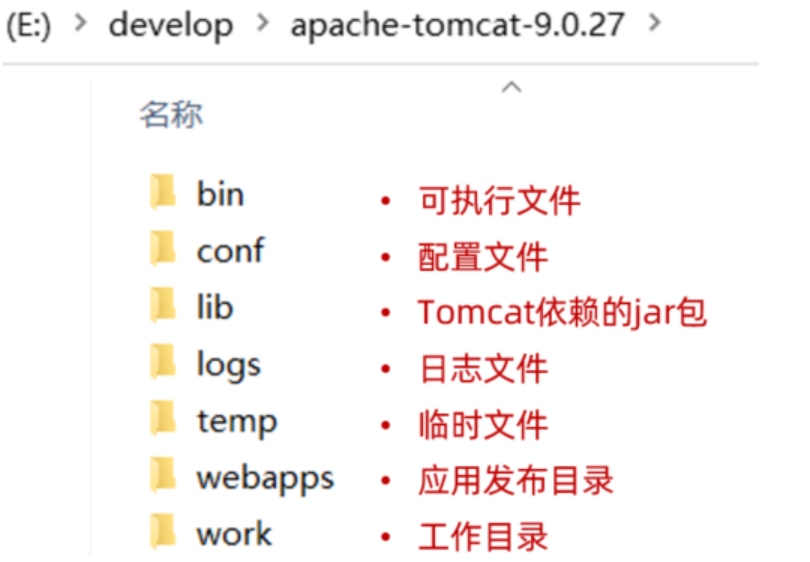
SpringBootWeb入门、HTTP协议、Web服务器-Tomcat
目录 一、SpringBootWeb入门 二、HTTP协议 HTTP-请求协议 HTTP-响应协议 HTTP-协议解析 三、Web服务器-Tomcat 服务器概述 Tomcat 一、SpringBootWeb入门 直接基于SpringFramework进行开发,存在两个问题:配置繁琐、入门难度大 通过springboot就…...
【Jenkins】Centos环境安装Jenkins(通过rpm安装)
在Centos操作系统中通过rpm安装Jenkins 参考官网 https://www.jenkins.io/doc/book/installing/linux/#red-hat-centos 1、下载安装Jdk17 下载安装 # 更新您的系统,不一定需要 # sudo yum -y update # 安装将用于下载 Java 17 二进制文件的 wget 命令行工具。 s…...
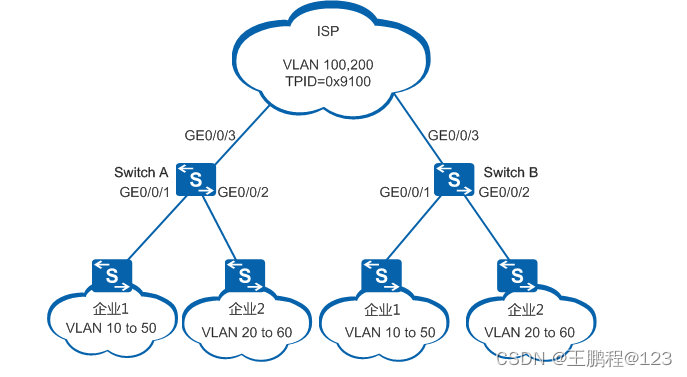
华为数通---配置基本QinQ示例
QinQ简介 定义 QinQ(802.1Q-in-802.1Q)技术是一项扩展VLAN空间的技术,通过在802.1Q标签报文的基础上再增加一层802.1Q的Tag来达到扩展VLAN空间的功能,可以使私网VLAN透传公网。由于在骨干网中传递的报文有两层802.1Q Tag&#x…...
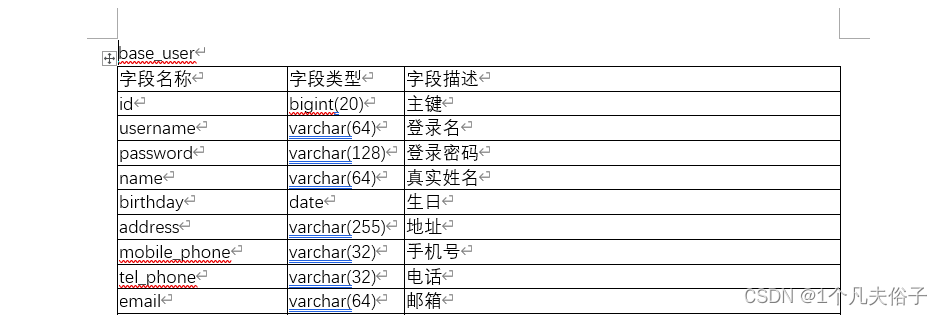
利用poi实现将数据库表字段信息导出到word中
研发文档对于开发人员来说都不陌生了,而研发文档里重要的一部分就是表结构设计,需要我们在word建个表格把我们数据库中的表字段信息填进去,表多的话靠我们手动去填非常累人!!! 因此作为开发人员可不可以写…...

深入浅出分析kafka客户端程序设计 ----- 生产者篇----万字总结
前面在深入理解kafka中提到的只是理论上的设计原理, 本篇讲得是基于c语言的kafka库的程序编写!!!!! 首先要编写生产者的代码,得先知道生产者的逻辑在代码上是怎么体现的 1.kafka生产者的逻辑 …...
)
粗到细语义(Coarse-to-Fine Semantics)
粗到细语义(Coarse-to-Fine Semantics)是一种深度学习模型的设计方法,它通过逐步细化的方式来理解文本中的语义信息。这种方法通常用于文本分类、情感分析、问答等任务中。 在粗到细语义中,模型首先从整体上理解文本的大致意思&a…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...
