【数据结构(十一·多路查找树)】B树、B+树、B*树(6)
文章目录
- 1. 二叉树 与 B树
- 1.1. 二叉树存在的问题
- 1.2. 多叉树 的概念
- 1.3. B树 的基本介绍
- 2. 多叉树——2-3树
- 2.1. 基本概念
- 2.2. 实例应用
- 2.3. 其他说明
- 3. B 树、B+树 和 B*树
- 3.1. B树 的介绍
- 3.2. B+树 的介绍
- 3.2. B*树 的介绍
1. 二叉树 与 B树
1.1. 二叉树存在的问题
二叉树的操作效率较高,但是也存在问题, 请看下面的二叉树

二叉树需要加载到内存的,如果二叉树的节点少,没有什么问题,但是如果二叉树的节点很多(比如 1 亿), 就存在如下问题:
问题 1:在构建二叉树时,需要多次进行 i/o 操作(海量数据存在数据库或文件中),节点海量,构建二叉树时,速度有影响
问题 2:节点海量,也会造成二叉树的高度很大,会降低操作速度。
1.2. 多叉树 的概念
在二叉树中,每个节点有数据项,最多有两个子节点。如果允许每个节点可以有更多的数据项和更多的子节点,就是多叉树(multiway tree),多叉树通过重新组织节点,减少树的高度,能对二叉树进行优化。
后面会讲到 2-3 树,2-3-4 树就是多叉树
举例说明:
下面2-3 树就是一颗多叉树
1.3. B树 的基本介绍
B 树通过重新组织节点,降低树的高度,并且减少 i/o 读写次数来提升效率。

- 如图 B 树通过重新组织节点, 降低了树的高度.
- 文件系统及数据库系统的设计者利用了磁盘预读原理,将一个节点的大小设为等于一个
页(页的大小通常为 4k),这样每个节点只需要一次 I/O 就可以完全载入 - 将
树的度M 设置为 1024,在 600 亿个元素中最多只需要 4 次 I/O 操作就可以读取到想要的元素,B 树(B+)广泛应用于文件存储系统以及数据库系统中
2. 多叉树——2-3树
2.1. 基本概念
2-3 树是最简单的 B 树结构, 具有如下特点:
① 2-3 树的所有叶子节点都在同一层(只要是 B 树都满足这个条件)
② 有两个子节点的节点叫二节点,二节点要么没有子节点,要么有两个子节点
③ 有三个子节点的节点叫三节点,三节点要么没有子节点,要么有三个子节点
④2-3 树是由二节点和三节点构成的树。
2.2. 实例应用
将数列{16, 24, 12, 32, 14, 26, 34, 10, 8, 28, 38, 20} 构建成 2-3 树,并保证数据插入的大小顺序。
构建结果如下:

插入规则:
- 2-3 树的所有叶子节点都在同一层.(只要是 B树都满足这个条件)
- 有两个子节点的节点叫二节点,二节点要么没有子节点,要么有两个子节点.
- 有三个子节点的节点叫三节点,三节点要么没有子节点,要么有三个子节点
- 当按照规则插入一个数到某个节点时,不能满足上面三个要求,就需要拆,先向上拆,如果上层满,则拆本层,拆后仍然需要满足上面 3 个条件。
- 对于三节点的子树的值大小仍然遵守(BST 二叉排序树)的规则
(这里关于如何构建2-3树讲并的不清楚,大家需要参考其他的资料学习)
2.3. 其他说明
除了 23 树,还有 234 树等,概念和 23 树类似,也是一种 B 树。 如图:

3. B 树、B+树 和 B*树
3.1. B树 的介绍
B-tree树即 B树,B 即 Balanced,平衡的意思。有人把 B-tree 翻译成 B-树,容易让人产生误解。会以为 B-树是一种树,而 B 树又是另一种树。实际上,B-树 就是指的 B 树。
前面已经介绍了 2-3树和 2-3-4树,他们就是 B树(英语:B-tree 也写成 B-树),这里我们再做一个说明,在学习 Mysql 时,经常听到说某种类型的索引是基于 B树 或者 B+树的,如图:

对上图的说明:
- B 树的阶:节点的最多子节点个数。比如 2-3 树的阶是 3,2-3-4 树的阶是 4
- B-树的搜索,从根结点开始,对结点内的关键字(有序)序列进行二分查找,如果命中则结束,否则进入查询关键字所属范围的儿子结点;重复,直到所对应的儿子指针为空,或已经是叶子结点
- 关键字集合分布在整颗树中, 即叶子节点和非叶子节点都存放数据.
- 搜索有可能在非叶子结点结束
5)其搜索性能等价于在关键字全集内做一次二分查找
3.2. B+树 的介绍
B+树是 B 树的变体,也是一种多路搜索树。

对上图的说明:
- B+树的搜索与 B 树也基本相同,区别是 B+树只有达到叶子结点才命中(B树可以在非叶子结点命中),其性能也等价于在关键字全集做一次二分查找
- 所有关键字都出现在叶子结点的链表中(即数据只能在叶子节点【也叫稠密索引】),且链表中的关键字(数据)恰好是有序的。
- 不可能在非叶子结点命中
- 非叶子结点相当于是叶子结点的索引(稀疏索引),叶子结点相当于是存储(关键字)数据的数据层
- 更适合文件索引系统
- B 树和 B+树各有自己的应用场景,不能说 B+树完全比 B 树好,反之亦然
3.2. B*树 的介绍
B*树是 B+树的变体,在 B+树的非根和非叶子结点再增加指向兄弟的指针。

B*树的说明:
- B*树定义了非叶子结点关键字个数至少为 (2/3)*M(树的度),即块的最低使用率为 2/3,而 B+树的块的最低使用率为的1/2。
- 从第 1 个特点我们可以看出,B*树分配新结点的概率比 B+树要低,空间使用率更高。
相关文章:

【数据结构(十一·多路查找树)】B树、B+树、B*树(6)
文章目录 1. 二叉树 与 B树1.1. 二叉树存在的问题1.2. 多叉树 的概念1.3. B树 的基本介绍 2. 多叉树——2-3树2.1. 基本概念2.2. 实例应用2.3. 其他说明 3. B 树、B树 和 B*树3.1. B树 的介绍3.2. B树 的介绍3.2. B*树 的介绍 1. 二叉树 与 B树 1.1. 二叉树存在的问题 二叉树…...

弟弟的作业
问题 G: 弟弟的作业 [命题人 : 外部导入] 时间限制 : 1.000 sec 内存限制 : 128 MB 题目描述 你的弟弟刚做完了“100以内数的加减法”这部分的作业,请你帮他检查一下。每道题目(包括弟弟的答案)的格式为abc或者a-bc,其中a和b是作…...

代码随想录算法训练营第37天|● 738.单调递增的数字 ● 968.监控二叉树 ● 总结
738. 单调递增的数字 中等 相关标签 相关企业 提示 当且仅当每个相邻位数上的数字 x 和 y 满足 x < y 时,我们称这个整数是单调递增的。 给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。 示例 1: 输入: n 10输出: …...

出现 java: 找不到符号 符号: 变量 log 的解决方法
目录 1. 问题所示2. 原理分析3. 解决方法3.1 增加编译参数3.2 增加lombok插件3.3 清楚本地缓存1. 问题所示 使用Springboot启动项目的时候,出现如下bug: java: 找不到符号符号: 变量 log位置: 类 org.springblade.example.consumer.rpc.BlogStu...
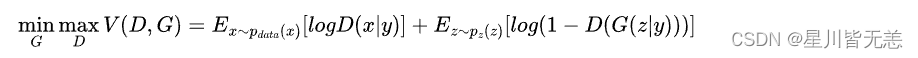
大数据机器学习与深度学习—— 生成对抗网络(GAN)
GAN概述 在讲GAN之前,先讲一个小趣事,你知道GAN是怎么被发明的吗?据Ian Goodfellow自己说: 之前他一直在研究生成模型,可能是一时兴起,有一天他在酒吧喝酒时,在酒吧里跟朋友讨论起生成模型。然…...

vue前端访问Django channels WebSocket失败
现象 前端报错:SSH.vue:51 WebSocket connection to ‘ws://127.0.0.1:8000/server/terminal/120.59.88.26/22/1/’ failed: 后端报错:Not Found: /server/terminal/120.79.83.26/22/1/ 原因 django的版本与channels的版本不匹配(django…...

厉害了!水浸监控技术有升级啦
水浸监控在今天的社会中变得愈发重要,特别是在各种行业和场所。面对突发的水灾,及时有效的监测和预警系统可以帮助组织减少损失,保障人员和财产的安全。 客户案例 商业办公楼 合肥某大型商业办公楼面临着水灾风险,而传统的监控系…...

【开题报告】基于SpringBoot的大学生心理教育平台的设计与实现
1.研究背景 大学生心理健康问题一直备受关注。随着社会压力的增加、人际关系的复杂化以及学业与就业压力等因素的影响,大学生心理健康问题日益突出。因此,设计并实现基于SpringBoot的大学生心理教育平台具有重要的研究意义和实践价值。 (1&…...
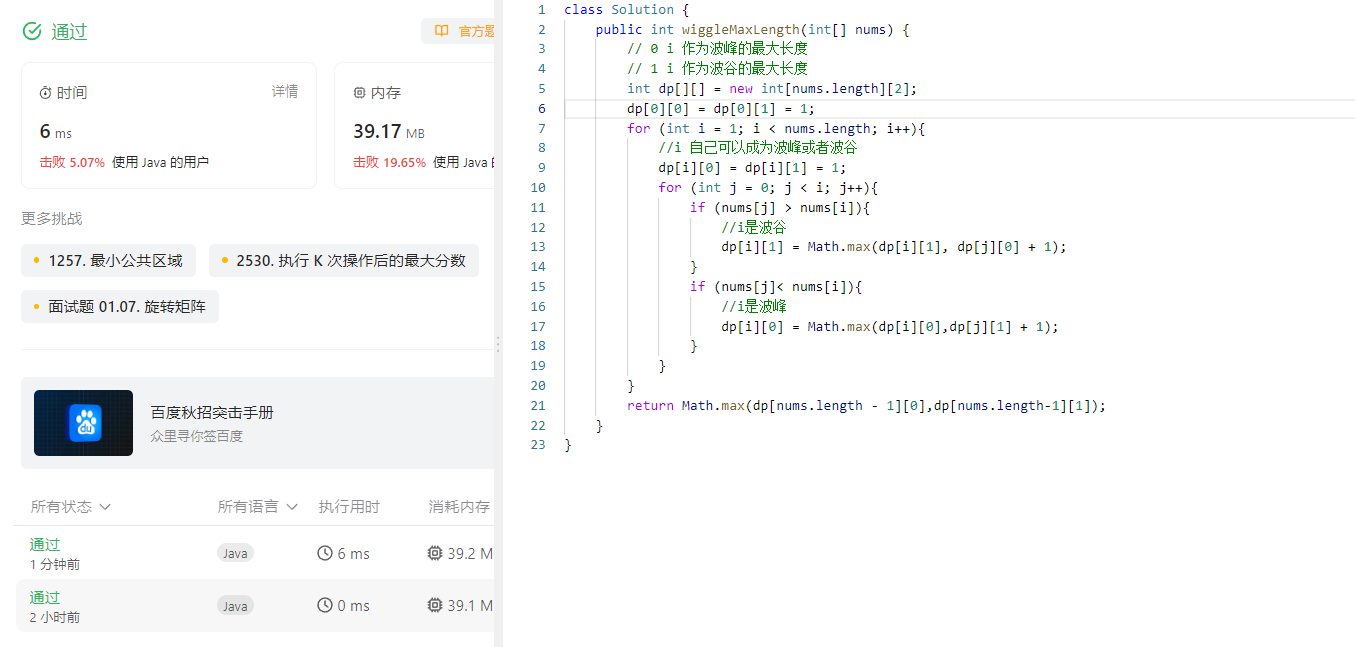
376. 摆动序列
376. 摆动序列 原题链接:完成情况:解题思路:参考代码:_376摆动序列_376摆动序列 错误经验吸取 原题链接: 376. 摆动序列 https://leetcode.cn/problems/wiggle-subsequence/description/ 完成情况: 解题…...

现在个人想上架微信小游戏已经这么难了吗...
引言 大家好,最近我突然想起来我还有一款微信小游戏还没有上架,于是捣鼓了一天把游戏完善了一下,然后准备提交审核,却发现异常的艰难... 1.为什么难? 相信大家都大概知道,自从微信平台宣布 9月1日起&…...
C语言数据结构-----二叉树(2)堆的深入理解及应用、链式二叉树的讲解及代码实现
前言 本篇文章讲述的内容有部分是上一节写过的。重复内容不会再进行说明,大家可以看上一节内容 链接: C语言数据结构-----二叉树(1)认识数、二叉树、堆及堆的代码实现 文章目录 前言1.使用堆解决TOP-K问题2.向下调整堆的时间复杂度与向上调整堆的时间复杂度对比3.堆…...

【算法】【动规】等差数列划分
跳转汇总链接 👉🔗算法题汇总链接 1.2 等差数列划分 🔗题目链接 如果一个数列 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该数列为等差数列。例如,[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是…...
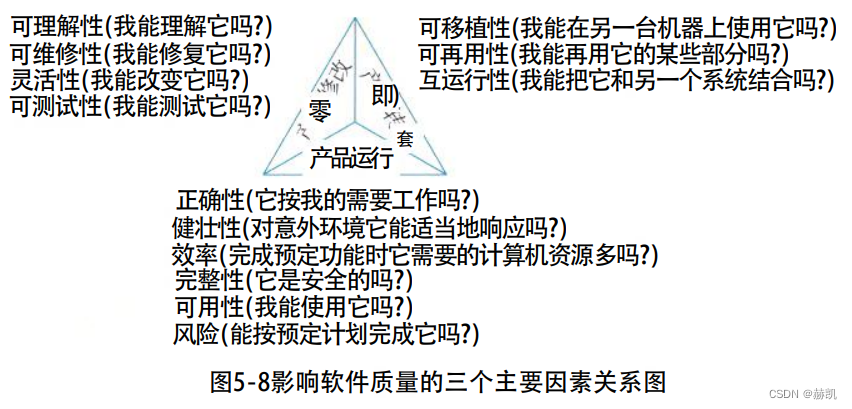
系统架构设计师教程(五)软件工程基础知识
软件工程基础知识 5.1 软件工程5.1.1 软件工程定义5.1.2 软件过程模型5.1.3 敏捷模型敏捷开发的特点敏捷方法的核心思想主要敏捷方法简介 5.1.4 统一过程模型 (RUP)RUP的生命周期RUP中的核心概念RUP的特点 5.1.5 软件能力成熟度模型 5.2 需求工程5.2.1 需求获取需求获取的基本步…...
计算机中的文件管理
操作系统对计算机的管理包括两个方面:硬件资源和软件资源。硬件资源的管理包括CPU 的管理、存储器的管理、设备管理等,主要解决硬件资源的有效和合理利用问题。 软件资源包括各种系统程序、各种应用程序、各种用户程序,也包括大量的文档材料、…...

Linux常见排错思路及命令
Linux常见排错思路及命令 一、引言 在Linux系统中,由于其高度可配置和可定制的特性,可能会遇到各种问题。本文将介绍一些常见的排错思路,并提供一些常用的命令,以帮助您快速定位和解决问题。 二、常见排错思路 查看系统日志 …...

【springboot】【easyexcel】excel文件读取
目录 pom.xmlExcelVo逐行读取并处理全部读取并处理向ExcelListener 传参 pom.xml <dependency><groupId>com.alibaba</groupId><artifactId>easyexcel</artifactId><version>3.1.1</version> </dependency>ExcelVo 字段映射…...
【STM32】ADC模数转换器
1 ADC简介 ADC(Analog-Digital Converter)模拟-数字转换器 ADC可以将引脚上连续变化的模拟电压转换为内存中存储的数字变量,建立模拟电路到数字电路的桥梁 STM32是数字电路,只有高低电平,没有几V电压的概念ÿ…...

Git篇---第九篇
系列文章目录 文章目录 系列文章目录前言一、使用过git merge和git rebase吗?它们之间有什么区别?二、使用过git cherry-pick,有什么作用?前言 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站,这篇文章男女通用,看…...

Paper Reading: (ACRST) 基于自适应类再平衡自训练的半监督目标检测
目录 简介工作重点方法CropBankFBRAFFRTwo-stage Pseudo-label Filtering 实验与SOTA比较消融实验 简介 题目:《Semi-Supervised Object Detection with Adaptive Class-Rebalancing Self-Training》,AAAI’22, 基于自适应类再平衡自训练的半…...

2023年贺岁电影:一眼多,二眼好多
如果从11月末开始统计,今年贺岁档共有72部贺岁片,平均一天就有2部电影上映,看完总计需要花费7400分钟。 这个数量几乎快赶上2021年到2022年贺岁片的总和。 今年电影市场快速回暖以来,多部爆款作品接力上映,持续刺激市…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

