ARMV8 - A64 - 函数调用,内存栈操作
说明
- 看了下ARM平台上C语言函数调用的反汇编代码,理清楚了其中的内存栈汇编操作,特整理下。
- 本文环境基于:ARMv8-a架构A53核soc,aarch64状态。
预先了解的知识点
内存栈
- 栈和栈帧的基本概念
- 重点:出栈入栈的单位不是单个局部变量,而是栈帧。
相关寄存器
- FP:Frame Pointer(栈帧指针),指向当前栈帧的顶部,在A53平台是使用通用寄存器x29保存。
- SP:Stack Pointer(栈顶指针),保存当前栈顶地址,在A53平台是一个特殊寄存器,不同异常等级是不同的寄存器,
- LR:Link Register(链接寄存器),保存子函数运行结束后的返回地址(跳转指令的下一条指令地址),在A53平台是使用通用寄存器x30充当,详细使用请看bl和ret指令说明。
- 问题:初次了解,不好理解和区分FP和SP的作用和角色,SP是全局唯一的保存栈顶地址的寄存器,而FP是保存单个函数的栈帧基址,调用新函数,入栈操作结束后,需要将SP的值赋值给FP,类似于:SP是全局变量,而x29是局部变量,虽然大部分时刻两个寄存器值是一样的。
相关汇编指令
- 函数调用实现原理,跳转和返回指令
- 内存操作store,load
实例
- C源码(a.c)
#include <stdio.h>int test1()
{return test(1, 2);
}int test(int a, int b)
{return a+b;
}int main()
{test1();return 0;
}
- 对应的汇编代码(aarch64-linux-gnu-gcc -S a.c)
.arch armv8-a.file "a.c".text.align 2.global test1.type test1, %function
test1:stp x29, x30, [sp, -16]!add x29, sp, 0mov w1, 2mov w0, 1bl testldp x29, x30, [sp], 16ret.size test1, .-test1.align 2.global test.type test, %function
test:sub sp, sp, #16str w0, [sp, 12]str w1, [sp, 8]ldr w1, [sp, 12]ldr w0, [sp, 8]add w0, w1, w0add sp, sp, 16ret.size test, .-test.align 2.global main.type main, %function
main:stp x29, x30, [sp, -16]!add x29, sp, 0bl test1mov w0, 0ldp x29, x30, [sp], 16ret.size main, .-main.ident "GCC: (Linaro GCC 6.3-2017.05) 6.3.1 20170404".section .note.GNU-stack,"",@progbits
说明
- 从汇编代码可以看出存在两种不同实现,如下:
- 函数调用栈中间函数(test1)
- 函数调用栈末端函数(test)
中间函数
test1:stp x29, x30, [sp, -16]! //将栈空间扩大16字节(更改sp寄存器值),再将x29,x30的数据(遗传自父函数)保存到栈顶 add x29, sp, 0 //将栈顶地址(sp)即此函数的栈帧基址保存到x29,... //函数操作(省略)bl test //跳转到test函数执行ldp x29, x30, [sp], 16 //将栈顶数据load到x29,x30中,再缩小栈空间16字节(即将sp恢复到父函数的栈顶)ret //返回父函数
末端函数
test:sub sp, sp, #16 //将sp保存的数据减小16字节,即将栈空间扩大16字节... //函数操作(省略)add sp, sp, 16 //将sp保存的数据增加16字节,即将栈空间缩小16字节ret
问题
- 为什么中间函数和末端函数实现不同,中间函数需要将x29,x30保存到栈内存中,最后再从栈内存中load到x29,x30中。
- 是因为中间函数(test1)bl指令调用末端函数(test)时,会覆盖掉x30的数据(原本保存的是父函数main,跳转test1的下一条指令),覆盖后中间函数(test1)的ret指令就跳不回main函数了,因此需要先将x30的数据保存到栈上,从子函数跳转回来后,需要将x29,x30的数据从栈上恢复。
- x29是栈帧指针,保存是当前函数的frame pointer,是约定俗成,因此需要保存和恢复,但是也不是必须,例如:test函数中就没有使用x29。
注意项
- sp 必须16Byte 对齐,扩大和缩小都必须是16字节的倍数。
相关文章:

ARMV8 - A64 - 函数调用,内存栈操作
说明 看了下ARM平台上C语言函数调用的反汇编代码,理清楚了其中的内存栈汇编操作,特整理下。本文环境基于:ARMv8-a架构A53核soc,aarch64状态。 预先了解的知识点 内存栈 栈和栈帧的基本概念重点:出栈入栈的单位不是…...

MyBatis 四大核心组件之 ResultSetHandler 源码解析
🚀 作者主页: 有来技术 🔥 开源项目: youlai-mall 🍃 vue3-element-admin 🍃 youlai-boot 🌺 仓库主页: Gitee 💫 Github 💫 GitCode 💖 欢迎点赞…...

docker-compose 单机容器编排
docker-compose 单机容器编排 Dockerfile:先配置好的文件,然后bulid,镜像容器。 docker-compose 既可以基于dockerfile,也可以基于镜像,一键式拉起镜像和容器。 docker-compose 核心就是yml文件,可以定义…...

springboot项目使用Layui作为前端UI的一系列前后端交互的解决方法
背景: 因为比较喜欢Layui,因为多个项目都是从零开始就使用的layui开发的,并且开发过程中借鉴了很多其他项目(如Ruoyi、Pear Admin),因此最终选用大部分Pear Admin的项目中使用的一系列解决方案,…...

【Linux】Firewalld防火墙新增端口、开启、查看等
Linux操作系统中,Firewalld防火墙相关操作如下: 安装 yum install firewalld firewalld-configFirewall开启常见端口命令 新增端口: firewall-cmd --zonepublic --add-port80/tcp --permanentfirewall-cmd --zonepublic --add-port443/tc…...

学习笔记 -- TVS管选型参考
一、TVS管基本工作原理 当TVS管(瞬态电压抑制器)两极受到反向瞬态高能量冲击时,能以纳秒(ns)量级的速度,将两极间的高阻抗变为低阻抗,使两极间的电压箝位于一个预定的值,有效地保护电子线路中的元器件。 在浪涌电压作用下…...
功能更新|免费敏捷工具Leangoo领歌私有部署新增第三方身份认证和API对接
Leangoo领歌是一款永久免费的专业的敏捷开发管理工具,提供端到端敏捷研发管理解决方案,涵盖敏捷需求管理、任务协同、进展跟踪、统计度量等。 Leangoo支持敏捷研发管理全流程,包括小型团队敏捷开发,规模化敏捷SAFe,Scr…...
重生奇迹mu战士加点
在重生奇迹MU中,战士作为一个近战职业,主要依赖于物理攻击来输出伤害。因此,在加点方面,战士需要优先考虑加强自身的攻击力,同时也要增强自身的生存能力和耐久度。 以下是可参考的战士加点方案: 1.力量&a…...

【数据结构(十一·多路查找树)】B树、B+树、B*树(6)
文章目录 1. 二叉树 与 B树1.1. 二叉树存在的问题1.2. 多叉树 的概念1.3. B树 的基本介绍 2. 多叉树——2-3树2.1. 基本概念2.2. 实例应用2.3. 其他说明 3. B 树、B树 和 B*树3.1. B树 的介绍3.2. B树 的介绍3.2. B*树 的介绍 1. 二叉树 与 B树 1.1. 二叉树存在的问题 二叉树…...

弟弟的作业
问题 G: 弟弟的作业 [命题人 : 外部导入] 时间限制 : 1.000 sec 内存限制 : 128 MB 题目描述 你的弟弟刚做完了“100以内数的加减法”这部分的作业,请你帮他检查一下。每道题目(包括弟弟的答案)的格式为abc或者a-bc,其中a和b是作…...

代码随想录算法训练营第37天|● 738.单调递增的数字 ● 968.监控二叉树 ● 总结
738. 单调递增的数字 中等 相关标签 相关企业 提示 当且仅当每个相邻位数上的数字 x 和 y 满足 x < y 时,我们称这个整数是单调递增的。 给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。 示例 1: 输入: n 10输出: …...

出现 java: 找不到符号 符号: 变量 log 的解决方法
目录 1. 问题所示2. 原理分析3. 解决方法3.1 增加编译参数3.2 增加lombok插件3.3 清楚本地缓存1. 问题所示 使用Springboot启动项目的时候,出现如下bug: java: 找不到符号符号: 变量 log位置: 类 org.springblade.example.consumer.rpc.BlogStu...
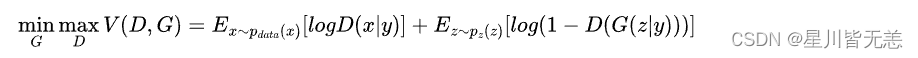
大数据机器学习与深度学习—— 生成对抗网络(GAN)
GAN概述 在讲GAN之前,先讲一个小趣事,你知道GAN是怎么被发明的吗?据Ian Goodfellow自己说: 之前他一直在研究生成模型,可能是一时兴起,有一天他在酒吧喝酒时,在酒吧里跟朋友讨论起生成模型。然…...

vue前端访问Django channels WebSocket失败
现象 前端报错:SSH.vue:51 WebSocket connection to ‘ws://127.0.0.1:8000/server/terminal/120.59.88.26/22/1/’ failed: 后端报错:Not Found: /server/terminal/120.79.83.26/22/1/ 原因 django的版本与channels的版本不匹配(django…...

厉害了!水浸监控技术有升级啦
水浸监控在今天的社会中变得愈发重要,特别是在各种行业和场所。面对突发的水灾,及时有效的监测和预警系统可以帮助组织减少损失,保障人员和财产的安全。 客户案例 商业办公楼 合肥某大型商业办公楼面临着水灾风险,而传统的监控系…...

【开题报告】基于SpringBoot的大学生心理教育平台的设计与实现
1.研究背景 大学生心理健康问题一直备受关注。随着社会压力的增加、人际关系的复杂化以及学业与就业压力等因素的影响,大学生心理健康问题日益突出。因此,设计并实现基于SpringBoot的大学生心理教育平台具有重要的研究意义和实践价值。 (1&…...
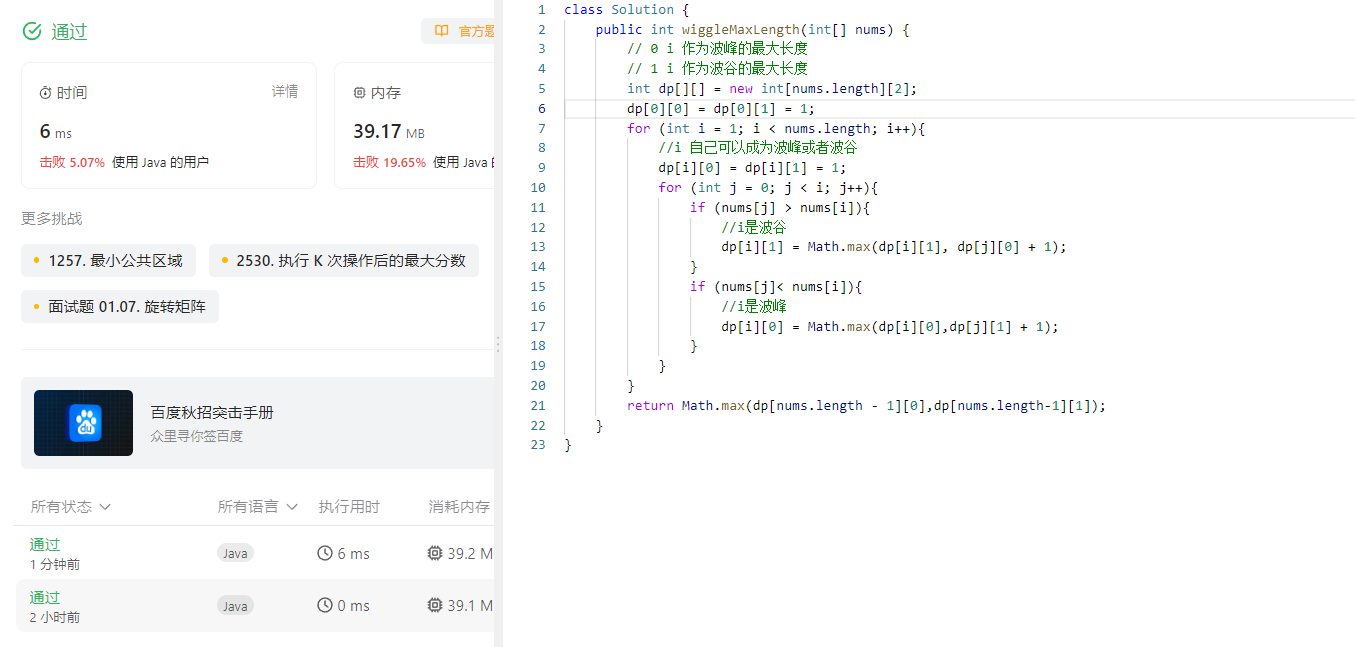
376. 摆动序列
376. 摆动序列 原题链接:完成情况:解题思路:参考代码:_376摆动序列_376摆动序列 错误经验吸取 原题链接: 376. 摆动序列 https://leetcode.cn/problems/wiggle-subsequence/description/ 完成情况: 解题…...

现在个人想上架微信小游戏已经这么难了吗...
引言 大家好,最近我突然想起来我还有一款微信小游戏还没有上架,于是捣鼓了一天把游戏完善了一下,然后准备提交审核,却发现异常的艰难... 1.为什么难? 相信大家都大概知道,自从微信平台宣布 9月1日起&…...
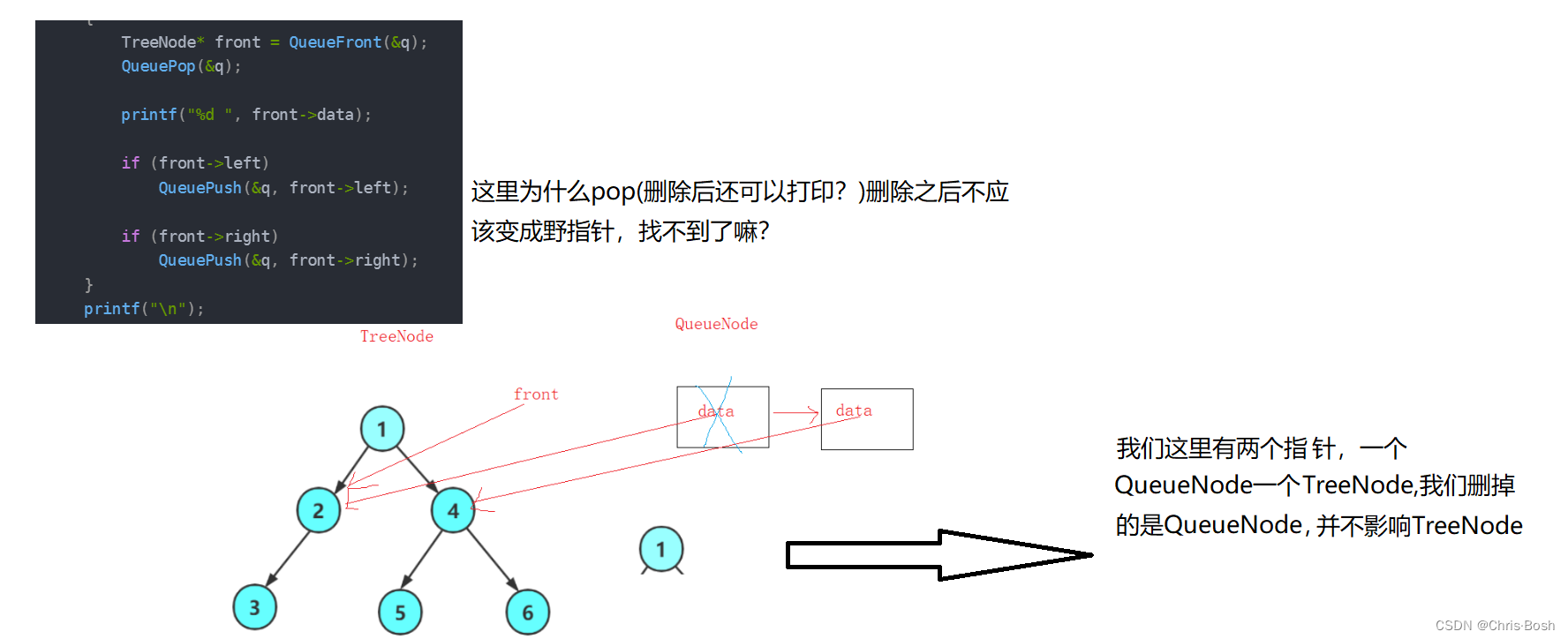
C语言数据结构-----二叉树(2)堆的深入理解及应用、链式二叉树的讲解及代码实现
前言 本篇文章讲述的内容有部分是上一节写过的。重复内容不会再进行说明,大家可以看上一节内容 链接: C语言数据结构-----二叉树(1)认识数、二叉树、堆及堆的代码实现 文章目录 前言1.使用堆解决TOP-K问题2.向下调整堆的时间复杂度与向上调整堆的时间复杂度对比3.堆…...

【算法】【动规】等差数列划分
跳转汇总链接 👉🔗算法题汇总链接 1.2 等差数列划分 🔗题目链接 如果一个数列 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该数列为等差数列。例如,[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...
