【一种用opencv实现高斯曲线拟合的方法】
背景:
项目中需要实现数据的高斯拟合,进而提取数据中标准差,手头只有opencv库,经过资料查找验证,总结该方法。
基础知识:
1、opencv中solve可以实现对矩阵参数的求解;
2、线的拟合就是对多项式参数求解的过程,多项式可表示为矩阵形式;
3、高斯公式中的指数幂,可以通过取对数的方式转变成多项式的形式;
求解思路:
高斯公式->多项式公式->矩阵参数->调用solve求解;
实现过程及代码
1、确定所选的高斯公式形式
G(x)=a*exp(-((x-b)/c)^2);
2、对于给定的输入x1 ~ xn,有对输出y1 ~ yn。可以形成如下等式:

对等式左右两边取对数,并进行变换,可形成如下形式


这里,就形成了AX^2+BX+C=Y的形式,其中

用A,B,C替换后后,原等式可写作

此时,我们只需要计算出A,B,C的值,再通过ABC与abc的关系即可得到abc的值。(请读者自行推导abc的公式,或见代码部分)
得到如上的多项式的形式后,直接构造参数矩阵,调用cv::solve(X,Y,A‘)接口,即可得到参数矩阵A’,其中即含有A,B,C的值。
上代码:
基础定义:
typedef struct StructMultinomialParamt
{double dB0;//多项式拟合的参数,数字表示幂次double dB1;double dB2;
}S_MULTNMNL_PARAMT;
typedef struct StructGaussParamT
{double dA;//指定的高斯参数double dB;//中心点double dC;//标准差
}S_GAUS_PARAMT;
void Gauss(S_GAUS_PARAMT sGsParamm, cv::Mat mX, cv::Mat& mY)
{cv::Mat mRslt = Mat::zeros(mX.size(), mX.type());double dx = 0;for (double i = 0.; i < mX.cols; i++){for (double j = 0.; j < mX.rows; j++){dx = mX.at<double>(j, i);mRslt.at<double>(j, i) = sGsParamm.dA * exp(-(pow((dx - sGsParamm.dB) / sGsParamm.dC, 2)));}}mY = mRslt;return;
}
高斯参数求解函数
void GaussFitT(cv::Mat mX, cv::Mat mY, S_GAUS_PARAMT* psGsParamm)
{//step1 构造参数矩阵mx与mycv::Mat X = Mat::zeros(mX.rows, 3, CV_64FC1);for (size_t i = 0; i < mX.rows; i++){for (size_t J = 0; J < 3; J++){X.at<double>(i, J) = pow(mX.at<double>(i, 0), 2 - J);}}cv::log(mY, mY);//对结果取对数//step2 多项式拟合cv::Mat A;//参数矩阵cv::solve(X, mY, A, cv::DECOMP_SVD);S_MULTNMNL_PARAMT sBparam;sBparam.dB2 = A.at<double>(0);sBparam.dB1 = A.at<double>(1);sBparam.dB0 = A.at<double>(2);//step3 高斯参数计算ABC-》abcpsGsParamm->dA = exp(sBparam.dB0 - pow(sBparam.dB1, 2) / (4 * sBparam.dB2));psGsParamm->dB = -sBparam.dB1 / (2 * sBparam.dB2);psGsParamm->dC = sqrt(-1 / sBparam.dB2);return;
}
# 测试代码
double dX[50];//输入数据X
double dY[50];//输入数据Y
std::vector<cv::Point> pointsOri;for (int i = 0; i < 50; i++)
{dX[i] = double(i);dY[i] = -0.5 * pow((dX[i] - 25), 2) + 320 + i;pointsOri.push_back(cv::Point(dX[i], dY[i]));
}
//转换成求解函数输入需要的数据格式
cv::Mat mGsInputX = Mat::zeros(50, 1, CV_64FC1);
cv::Mat mGsInputY = Mat::zeros(50, 1, CV_64FC1);
for (size_t i = 0; i < 50; i++)
{mGsInputX.at<double>(i) = dX[i];mGsInputY.at<double>(i) = dY[i];
}S_GAUS_PARAMT sGsParamm;//求解结果
GaussFitT(mGsInputX, mGsInputY, &sGsParamm);//结果对比
Mat mGsOutputY;
Gauss(sGsParamm, mGsInputX, mGsOutputY);
std::vector<cv::Point> pointsNew;//拟合结果
for (int i = 0; i < 50; i++)
{pointsNew.push_back(cv::Point(dX[i], mGsOutputY.at<double>(i)));
}
cv::Mat img(450, 60, CV_8UC3, cv::Scalar(0, 0, 0));
cv::polylines(img, std::vector<std::vector<cv::Point>>{pointsOri}, false, cv::Scalar(0, 0, 255), 2);
cv::polylines(img, std::vector<std::vector<cv::Point>>{pointsNew}, false, cv::Scalar(255, 255, 255), 0.5);// 显示图像
cv::imshow("Line Chart", img);
cv::waitKey(0);
运行输出

红色的为原始数据分布,白色的为拟合计算结果。
而我需要的标准差,则为sGsParamm.dC。
参考:https://blog.csdn.net/guangjie2333/article/details/115629152
https://blog.csdn.net/KYJL888/article/details/103073956
https://blog.csdn.net/qq_35097289/article/details/103910984
后记:
调用solve的接口求解时,OPENCV提供了以下六种方式以对应不同的情况。对于多项式的求解,也可以采用最小二乘法的逼近,不再调用solve方法,这块后面再填坑吧。
cv::DECOMP_LU 高斯消元法(LU分解)
cv::DECOMP_SVD 奇异值分解(SVD)
cv::DECOMP_CHOLESKY 对于对称正定矩阵
cv::DECOMP_EIG 特征值分解,只用于对称矩阵
cv::DECOMP_QR QR因式分解
cv::DECOMP_NORMAL 可选附加标志,表示要求解标准方程
相关文章:

【一种用opencv实现高斯曲线拟合的方法】
背景: 项目中需要实现数据的高斯拟合,进而提取数据中标准差,手头只有opencv库,经过资料查找验证,总结该方法。 基础知识: 1、opencv中solve可以实现对矩阵参数的求解; 2、线的拟合就是对多项…...

find_package 和 find_library的区别
背景 经常看CMakeLists.txt中有find_package和find_library,有时候没留意以为都一样,其实二者差距比较大,下面简单记录一下。 find_package find_package(NAME), 这段代码的本质就是在找一个NAME.cmake这个文件,一般在安装库的…...

socket是如何进行通信的
Socket通信的原理大致分为以下几个步骤: 服务器端建立Socket,开始侦听整个网络中的连接请求。当检测到来自客户端的连接请求时,向客户端发送收到连接请求的信息,并建立与客户端之间的连接。当完成通信后,服务器关闭与…...
STM32-固件打包部署
STM32-固件打包部署 Fang XS.1452512966qq.com STM32固件输出 工程上使用Keil开发STM32软件;在调试过程中,可直接编译下载;例如bootloader和APP,在调试时,可以直接下载2次;但是工程上,需要大…...
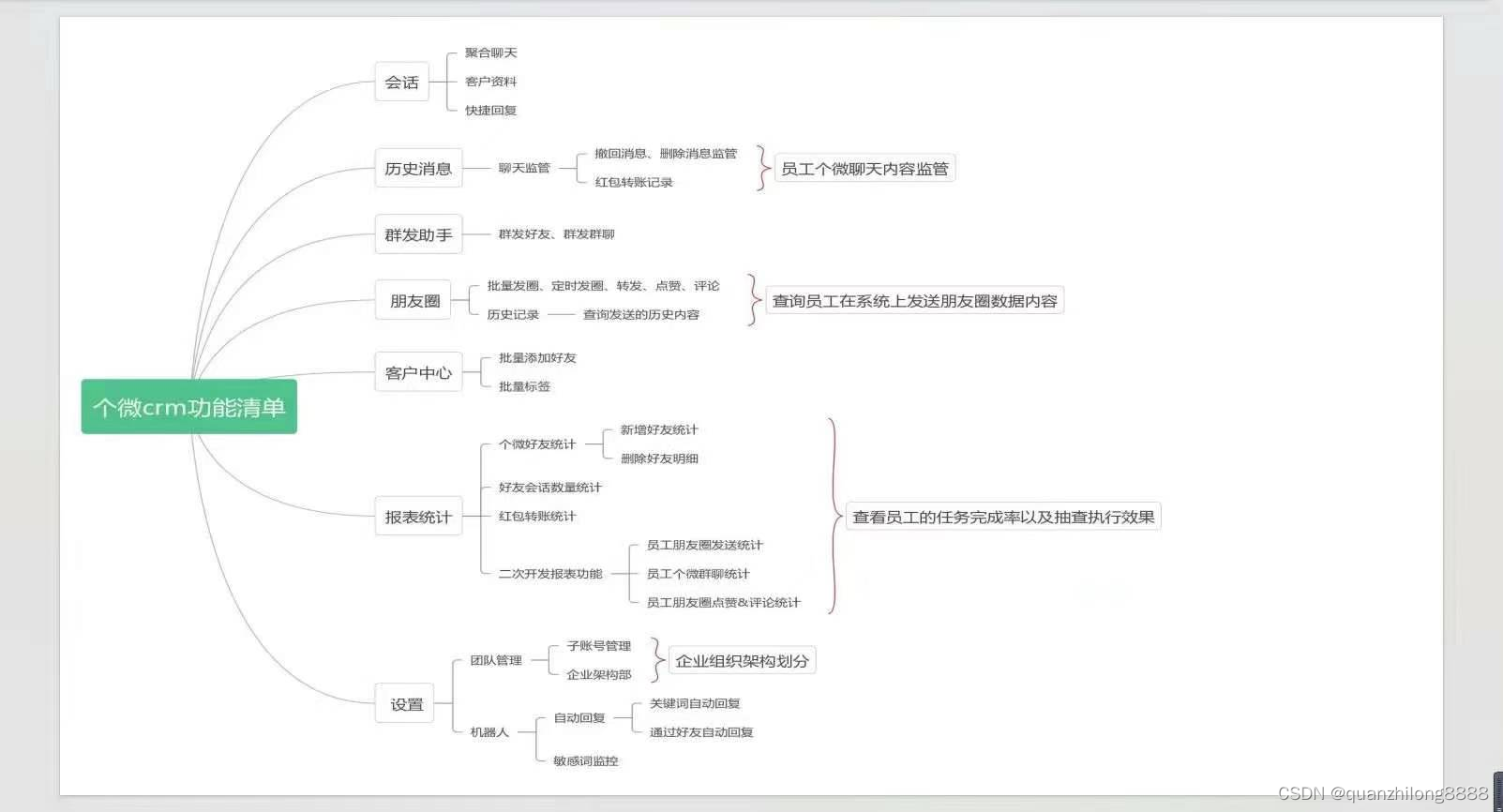
微信机器人如何使用?好用吗?好奇
随着微信的使用范围越来越大,所以人一多,管理起来就会遇到很多繁琐的情况需要仍去操作。 比如需要手动一个个通过好友验证,发消息,相同问题一遍遍的回答,消息还容易看漏,回复不过来...... 想着如果有什么可…...

ARMV8 - A64 - 函数调用,内存栈操作
说明 看了下ARM平台上C语言函数调用的反汇编代码,理清楚了其中的内存栈汇编操作,特整理下。本文环境基于:ARMv8-a架构A53核soc,aarch64状态。 预先了解的知识点 内存栈 栈和栈帧的基本概念重点:出栈入栈的单位不是…...

MyBatis 四大核心组件之 ResultSetHandler 源码解析
🚀 作者主页: 有来技术 🔥 开源项目: youlai-mall 🍃 vue3-element-admin 🍃 youlai-boot 🌺 仓库主页: Gitee 💫 Github 💫 GitCode 💖 欢迎点赞…...

docker-compose 单机容器编排
docker-compose 单机容器编排 Dockerfile:先配置好的文件,然后bulid,镜像容器。 docker-compose 既可以基于dockerfile,也可以基于镜像,一键式拉起镜像和容器。 docker-compose 核心就是yml文件,可以定义…...

springboot项目使用Layui作为前端UI的一系列前后端交互的解决方法
背景: 因为比较喜欢Layui,因为多个项目都是从零开始就使用的layui开发的,并且开发过程中借鉴了很多其他项目(如Ruoyi、Pear Admin),因此最终选用大部分Pear Admin的项目中使用的一系列解决方案,…...

【Linux】Firewalld防火墙新增端口、开启、查看等
Linux操作系统中,Firewalld防火墙相关操作如下: 安装 yum install firewalld firewalld-configFirewall开启常见端口命令 新增端口: firewall-cmd --zonepublic --add-port80/tcp --permanentfirewall-cmd --zonepublic --add-port443/tc…...

学习笔记 -- TVS管选型参考
一、TVS管基本工作原理 当TVS管(瞬态电压抑制器)两极受到反向瞬态高能量冲击时,能以纳秒(ns)量级的速度,将两极间的高阻抗变为低阻抗,使两极间的电压箝位于一个预定的值,有效地保护电子线路中的元器件。 在浪涌电压作用下…...
功能更新|免费敏捷工具Leangoo领歌私有部署新增第三方身份认证和API对接
Leangoo领歌是一款永久免费的专业的敏捷开发管理工具,提供端到端敏捷研发管理解决方案,涵盖敏捷需求管理、任务协同、进展跟踪、统计度量等。 Leangoo支持敏捷研发管理全流程,包括小型团队敏捷开发,规模化敏捷SAFe,Scr…...
重生奇迹mu战士加点
在重生奇迹MU中,战士作为一个近战职业,主要依赖于物理攻击来输出伤害。因此,在加点方面,战士需要优先考虑加强自身的攻击力,同时也要增强自身的生存能力和耐久度。 以下是可参考的战士加点方案: 1.力量&a…...

【数据结构(十一·多路查找树)】B树、B+树、B*树(6)
文章目录 1. 二叉树 与 B树1.1. 二叉树存在的问题1.2. 多叉树 的概念1.3. B树 的基本介绍 2. 多叉树——2-3树2.1. 基本概念2.2. 实例应用2.3. 其他说明 3. B 树、B树 和 B*树3.1. B树 的介绍3.2. B树 的介绍3.2. B*树 的介绍 1. 二叉树 与 B树 1.1. 二叉树存在的问题 二叉树…...

弟弟的作业
问题 G: 弟弟的作业 [命题人 : 外部导入] 时间限制 : 1.000 sec 内存限制 : 128 MB 题目描述 你的弟弟刚做完了“100以内数的加减法”这部分的作业,请你帮他检查一下。每道题目(包括弟弟的答案)的格式为abc或者a-bc,其中a和b是作…...

代码随想录算法训练营第37天|● 738.单调递增的数字 ● 968.监控二叉树 ● 总结
738. 单调递增的数字 中等 相关标签 相关企业 提示 当且仅当每个相邻位数上的数字 x 和 y 满足 x < y 时,我们称这个整数是单调递增的。 给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。 示例 1: 输入: n 10输出: …...

出现 java: 找不到符号 符号: 变量 log 的解决方法
目录 1. 问题所示2. 原理分析3. 解决方法3.1 增加编译参数3.2 增加lombok插件3.3 清楚本地缓存1. 问题所示 使用Springboot启动项目的时候,出现如下bug: java: 找不到符号符号: 变量 log位置: 类 org.springblade.example.consumer.rpc.BlogStu...
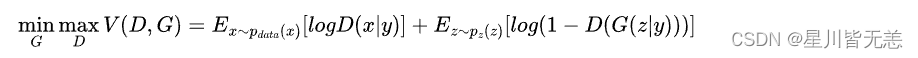
大数据机器学习与深度学习—— 生成对抗网络(GAN)
GAN概述 在讲GAN之前,先讲一个小趣事,你知道GAN是怎么被发明的吗?据Ian Goodfellow自己说: 之前他一直在研究生成模型,可能是一时兴起,有一天他在酒吧喝酒时,在酒吧里跟朋友讨论起生成模型。然…...

vue前端访问Django channels WebSocket失败
现象 前端报错:SSH.vue:51 WebSocket connection to ‘ws://127.0.0.1:8000/server/terminal/120.59.88.26/22/1/’ failed: 后端报错:Not Found: /server/terminal/120.79.83.26/22/1/ 原因 django的版本与channels的版本不匹配(django…...

厉害了!水浸监控技术有升级啦
水浸监控在今天的社会中变得愈发重要,特别是在各种行业和场所。面对突发的水灾,及时有效的监测和预警系统可以帮助组织减少损失,保障人员和财产的安全。 客户案例 商业办公楼 合肥某大型商业办公楼面临着水灾风险,而传统的监控系…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...
