洛谷 P8794 [蓝桥杯 2022 国 A] 环境治理
文章目录
- [蓝桥杯 2022 国 A] 环境治理
- 题目链接
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 思路解析
- CODE
- 给点思考
[蓝桥杯 2022 国 A] 环境治理
题目链接
https://www.luogu.com.cn/problem/P8794
题目描述
LQ 国拥有 n n n 个城市,从 0 0 0 到 n − 1 n - 1 n−1 编号,这 n n n 个城市两两之间都有且仅有一条双向道路连接,这意味着任意两个城市之间都是可达的。每条道路都有一个属性 D D D,表示这条道路的灰尘度。当从一个城市 A 前往另一个城市 B 时,可能存在多条路线,每条路线的灰尘度定义为这条路线所经过的所有道路的灰尘度之和,LQ 国的人都很讨厌灰尘,所以他们总会优先选择灰尘度最小的路线。
LQ 国很看重居民的出行环境,他们用一个指标 P P P 来衡量 LQ 国的出行环境, P P P 定义为:
P = ∑ i = 0 n − 1 ∑ j = 0 n − 1 d ( i , j ) P=\sum \limits_{i=0}^{n-1} \sum \limits_{j=0}^{n-1} d(i,j) P=i=0∑n−1j=0∑n−1d(i,j)
其中 d ( i , j ) d(i,j) d(i,j) 表示城市 i i i 到城市 j j j 之间灰尘度最小的路线对应的灰尘度的值。
为了改善出行环境,每个城市都要有所作为,当某个城市进行道路改善时,会将与这个城市直接相连的所有道路的灰尘度都减少 1 1 1,但每条道路都有一个灰尘度的下限值 L L L,当灰尘度达到道路的下限值时,无论再怎么改善,道路的灰尘度也不会再减小了。
具体的计划是这样的:
- 第 1 1 1 天, 0 0 0 号城市对与其直接相连的道路环境进行改善;
- 第 2 2 2 天, 1 1 1 号城市对与其直接相连的道路环境进行改善;
……
- 第 n n n 天, n − 1 n - 1 n−1 号城市对与其直接相连的道路环境进行改善;
- 第 n + 1 n + 1 n+1 天, 0 0 0 号城市对与其直接相连的道路环境进行改善;
- 第 n + 2 n + 2 n+2 天, 1 1 1 号城市对与其直接相连的道路环境进行改善;
……
LQ 国想要使得 P P P 指标满足 P ≤ Q P \leq Q P≤Q。请问最少要经过多少天之后, P P P 指标可以满足 P ≤ Q P \leq Q P≤Q。如果在初始时就已经满足条件,则输出 0 0 0;如果永远不可能满足,则输出 − 1 -1 −1。
输入格式
输入的第一行包含两个整数 n , Q n, Q n,Q,用一个空格分隔,分别表示城市个数和期望达到的 P P P 指标。
接下来 n n n 行,每行包含 n n n 个整数,相邻两个整数之间用一个空格分隔,其中第 i i i 行第 j j j 列的值 D i , j ( D i , j = D j , i , D i , i = 0 ) D_{i,j} (D_{i,j}=D_{j,i},D_{i,i} = 0) Di,j(Di,j=Dj,i,Di,i=0) 表示城市 i i i 与城市 j j j 之间直接相连的那条道路的灰尘度。
接下来 n n n 行,每行包含 n n n 个整数,相邻两个整数之间用一个空格分隔,其中第 i i i 行第 j j j 列的值 L i , j ( L i , j = L j , i , L i , i = 0 ) L_{i,j} (L_{i,j} = L_{j,i}, L_{i,i} = 0) Li,j(Li,j=Lj,i,Li,i=0) 表示城市 i i i 与城市 j j j 之间直接相连的那条道路的灰尘度的下限值。
输出格式
输出一行包含一个整数表示答案。
样例 #1
样例输入 #1
3 10
0 2 4
2 0 1
4 1 0
0 2 2
2 0 0
2 0 0
样例输出 #1
2
提示
【样例说明】
初始时的图如下所示,每条边上的数字表示这条道路的灰尘度:
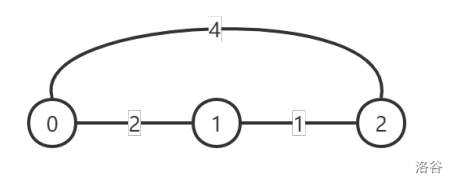
此时每对顶点之间的灰尘度最小的路线对应的灰尘度为:
- d ( 0 , 0 ) = 0 , d ( 0 , 1 ) = 2 , d ( 0 , 2 ) = 3 d(0, 0) = 0, d(0, 1) = 2, d(0, 2) = 3 d(0,0)=0,d(0,1)=2,d(0,2)=3;
- d ( 1 , 0 ) = 2 , d ( 1 , 1 ) = 0 , d ( 1 , 2 ) = 1 d(1, 0) = 2, d(1, 1) = 0, d(1, 2) = 1 d(1,0)=2,d(1,1)=0,d(1,2)=1;
- d ( 2 , 0 ) = 3 , d ( 2 , 1 ) = 1 , d ( 2 , 2 ) = 0 d(2, 0) = 3, d(2, 1) = 1, d(2, 2) = 0 d(2,0)=3,d(2,1)=1,d(2,2)=0。
初始时的 P P P 指标为 ( 2 + 3 + 1 ) × 2 = 12 (2 + 3 + 1) \times 2 = 12 (2+3+1)×2=12,不满足 P ≤ Q = 10 P \leq Q = 10 P≤Q=10;
第一天, 0 0 0 号城市进行道路改善,改善后的图示如下:
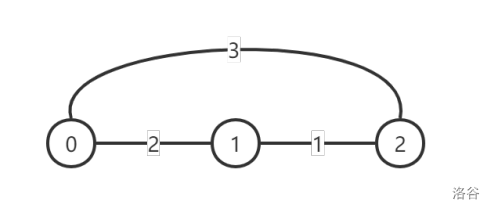
注意到边 ( 0 , 2 ) (0, 2) (0,2) 的值减小了 1 1 1,但 ( 0 , 1 ) (0, 1) (0,1) 并没有减小,因为 L 0 , 1 = 2 L_{0,1} = 2 L0,1=2 ,所以 ( 0 , 1 ) (0, 1) (0,1) 的值不可以再减小了。此时每对顶点之间的灰尘度最小的路线对应的灰尘度为:
- d ( 0 , 0 ) = 0 , d ( 0 , 1 ) = 2 , d ( 0 , 2 ) = 3 d(0, 0) = 0, d(0, 1) = 2, d(0, 2) = 3 d(0,0)=0,d(0,1)=2,d(0,2)=3,
- d ( 1 , 0 ) = 2 , d ( 1 , 1 ) = 0 , d ( 1 , 2 ) = 1 d(1, 0) = 2, d(1, 1) = 0, d(1, 2) = 1 d(1,0)=2,d(1,1)=0,d(1,2)=1,
- d ( 2 , 0 ) = 3 , d ( 2 , 1 ) = 1 , d ( 2 , 2 ) = 0 d(2, 0) = 3, d(2, 1) = 1, d(2, 2) = 0 d(2,0)=3,d(2,1)=1,d(2,2)=0。
此时 P P P 仍为 12 12 12。
第二天,1 号城市进行道路改善,改善后的图示如下:

此时每对顶点之间的灰尘度最小的路线对应的灰尘度为:
- d ( 0 , 0 ) = 0 , d ( 0 , 1 ) = 2 , d ( 0 , 2 ) = 2 d(0, 0) = 0, d(0, 1) = 2, d(0, 2) = 2 d(0,0)=0,d(0,1)=2,d(0,2)=2,
- d ( 1 , 0 ) = 2 , d ( 1 , 1 ) = 0 , d ( 1 , 2 ) = 0 d(1, 0) = 2, d(1, 1) = 0, d(1, 2) = 0 d(1,0)=2,d(1,1)=0,d(1,2)=0,
- d ( 2 , 0 ) = 2 , d ( 2 , 1 ) = 0 , d ( 2 , 2 ) = 0 d(2, 0) = 2, d(2, 1) = 0, d(2, 2) = 0 d(2,0)=2,d(2,1)=0,d(2,2)=0。
此时的 P P P 指标为 ( 2 + 2 ) × 2 = 8 < Q (2 + 2) \times 2 = 8 < Q (2+2)×2=8<Q,此时已经满足条件。
所以答案是 2 2 2。
【评测用例规模与约定】
- 对于 30 % 30\% 30% 的评测用例, 1 ≤ n ≤ 10 1 \leq n \leq 10 1≤n≤10, 0 ≤ L i , j ≤ D i , j ≤ 10 0 \leq L_{i,j} \leq D_{i,j} \leq 10 0≤Li,j≤Di,j≤10;
- 对于 60 % 60\% 60% 的评测用例, 1 ≤ n ≤ 50 1 \leq n \leq 50 1≤n≤50, 0 ≤ L i , j ≤ D i , j ≤ 1 0 5 0 \leq L_{i,j} \leq D_{i,j} \leq 10^5 0≤Li,j≤Di,j≤105;
- 对于所有评测用例, 1 ≤ n ≤ 100 1 \leq n \leq 100 1≤n≤100, 0 ≤ L i , j ≤ D i , j ≤ 1 0 5 0 \leq L_{i,j} \leq D_{i,j} \leq 10^5 0≤Li,j≤Di,j≤105, 0 ≤ Q ≤ 2 31 − 1 0 \leq Q \leq 2^{31} - 1 0≤Q≤231−1。
蓝桥杯 2022 国赛 A 组 F 题。
思路解析
很显然是一道 F l o y d Floyd Floyd,可以直接算出多源最短路各点权值。
但是还有个问题:清洁道路减少的灰尘度怎么算?如果按顺序每天更新道路灰尘度,复杂度为 O ( n 3 × k ) O(n^3 \times k) O(n3×k), k k k 为天数,当很显然可能超时,那我们怎么知道最少需要多少天呢?
- 一开始我想用队列来存权值变化的节点,然后更新其他节点值再入队来达到更新所有节点最短路的问题,但是失败了,因为这样就变成了针对队头节点的单源最短路了。
那么应该怎么办?答案是:二分。
我们可以发现:随着天数增加,街道灰尘度单调不增,所以可以用二分来猜答案,每次二分更新街道灰尘度,然后进行 F l o y d Floyd Floyd。这样复杂度就是 O ( n 3 ⋅ l o g k ) O(n^3·logk) O(n3⋅logk),能过。
CODE
#include <iostream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <queue>
#define ll long long
#define INF 0x3f3f3f3f using namespace std;typedef pair<int, int> pii;const int N = 110;
int n, Q; // n 是城市的数量,Q 是灰尘度之和的限制
int d[N][N], g[N][N], mini[N][N]; // d[i][j] 表示第 i 个城市和第 j 个城市之间的灰尘度,g[i][j] 表示初始的灰尘度,mini[i][j] 表示最小的灰尘度void floyd(){ // 弗洛伊德算法,用于更新所有城市之间的最短路径(即最小灰尘度)for(int k = 1; k <= n; ++k)for(int i = 1; i <= n; ++i)for(int j = 1; j <= n; ++j)d[i][j] = min(d[i][j], (d[i][k] == INF || d[k][j] == INF) ? INF : d[i][k] + d[k][j]);
}int all(){ // 计算所有城市之间的灰尘度之和int res = 0;for(int i = 1; i <= n; ++i)for(int j = 1; j <= n; ++j)res += d[i][j];return res;
}bool check(int x){ // 检查给定的清洁人数和城市编号是否满足条件int clean = x / n; // 清洁人数int city = x % n; // 城市编号for(int i = 1; i <= n; ++i)for(int j = 1; j <= n; ++j)d[i][j] = g[i][j]; // 恢复初始的灰尘度if(x){ for(int i = 1; i <= n; ++i){for(int j = 1; j <= n; ++j){int dif;if(i <= city) dif = clean + 1; // 如果城市编号小于等于给定的编号,那么清洁人数加一else dif = clean;d[i][j] = max(d[i][j] - dif, mini[i][j]); // 更新灰尘度,不能低于最小值d[j][i] = max(d[j][i] - dif, mini[j][i]);}}}floyd(); // 更新最短路径if(all() > Q) return false; // 如果灰尘度之和超过限制,返回 falseelse return true;
}int main(){cin >> n >> Q; // 输入城市数量和限制int dis;for(int i = 1; i <= n; ++i){for(int j = 1; j <= n; ++j){scanf("%d", &dis); // 输入初始的灰尘度g[i][j] = dis;}}for(int i = 1; i <= n; ++i){for(int j = 1; j <= n; ++j){scanf("%d", &dis); // 输入最小的灰尘度mini[i][j] = dis;}}int l = 0, r = INF, flag = 0, ans = -1;while(l < r){ // 使用二分搜索来找到最小的清洁人数和城市编号int mid = (l + r) >> 1;if(check(mid)) r = mid, ans = mid; // 如果满足条件,那么更新右边界和答案else l = mid + 1; // 否则更新左边界}printf("%d\n", ans); // 输出答案
}
给点思考
- 二分这步很妙,看似简单,但是想到不太容易,还是蒟蒻我练少了 >_<
- 每次更新街道的灰尘度,由于是无向图,所以要将双向边都更新。
相关文章:

洛谷 P8794 [蓝桥杯 2022 国 A] 环境治理
文章目录 [蓝桥杯 2022 国 A] 环境治理题目链接题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 提示 思路解析CODE给点思考 [蓝桥杯 2022 国 A] 环境治理 题目链接 https://www.luogu.com.cn/problem/P8794 题目描述 LQ 国拥有 n n n 个城市,从 0 0 …...

力扣面试150题 | 买卖股票的最佳时期
力扣面试150题 | 买卖股票的最佳时期 题目描述解题思路代码实现 题目描述 121.买卖股票的最佳时期 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一…...
uniapp 之 图片 视频 文件上传
<view class"" style"padding: 24rpx 0"><text>相关资料 <text class"fs-26 color-666">(图片、视频、文档不超过9个)</text> </text><view class"flex align-center" style&…...

MIT线性代数笔记-第28讲-正定矩阵,最小值
目录 28.正定矩阵,最小值打赏 28.正定矩阵,最小值 由第 26 26 26讲的末尾可知在矩阵为实对称矩阵时,正定矩阵有以下四种判定方法(都是充要条件): 所有特征值都为正左上角所有 k k k阶子矩阵行列式都为正&…...
Python:五种算法RFO、GWO、DBO、HHO、SSA求解23个测试函数
一、五种算法介绍 (1)红狐优化算法(Red fox optimization,RFO) (2)灰狼优化算法(Grey Wolf Optimizer,GWO) (3)蜣螂优化算法(Dung beetle opti…...

如何参与开源项目
大家好,受卡哥邀请,和大家分享一下开源活动的相关经验。首先简要自我介绍一下,我目前在一所985研二在读,主要学习大数据方向,从去年开始参与开源活动近一年时间,也对多个Apache框架有所贡献。 由于学校或专…...
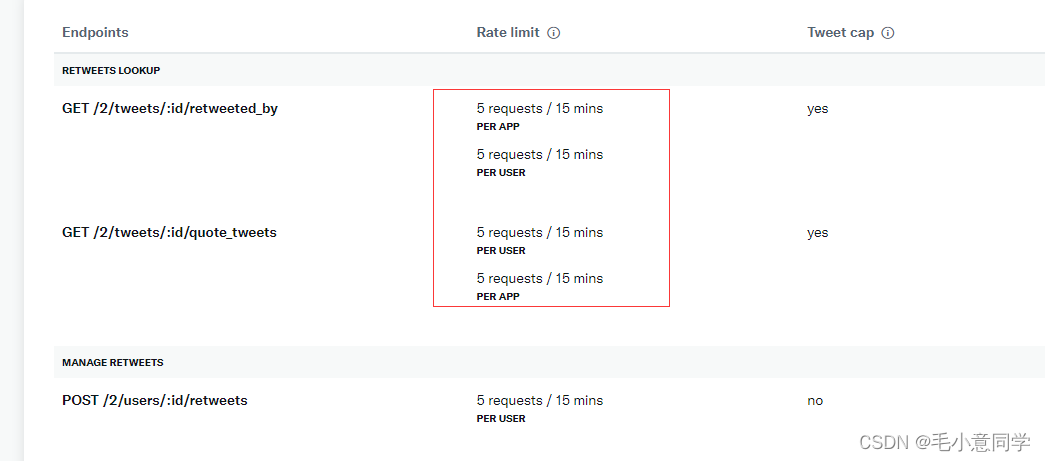
twitter开发如何避坑
此篇介绍在twitter开发过程中遇到的坑(尤其是费用的坑)。 一坑:免费接口少! 刚开始申请免费API使用的时候,twitter官方只会给你三个免费接口使用。 发twitter、删推文、查看用户信息。 这三个接口远远不够开发中使用…...
人工智能算法合集
人工智能(Artificial Intelligence,AI)作为当今世界最热门的技术领域之一,正日益改变着我们的生活方式、工作方式甚至整个社会结构。在人工智能领域中,算法是至关重要的一环,它们是实现人工智能技术应用的核…...

PythonStudio:一款国人写的python及窗口开发编辑IDE,可以替代pyqt designer等设计器了
本款软件只有十几兆,功能算是强大的,国人写的,很不错的python界面IDE.顶部有下载链接。下面有网盘下载链接,或者从官网直接下载。 目前产品免费,以后估计会有收费版本。主页链接:PythonStudio-硅量实验室 作…...
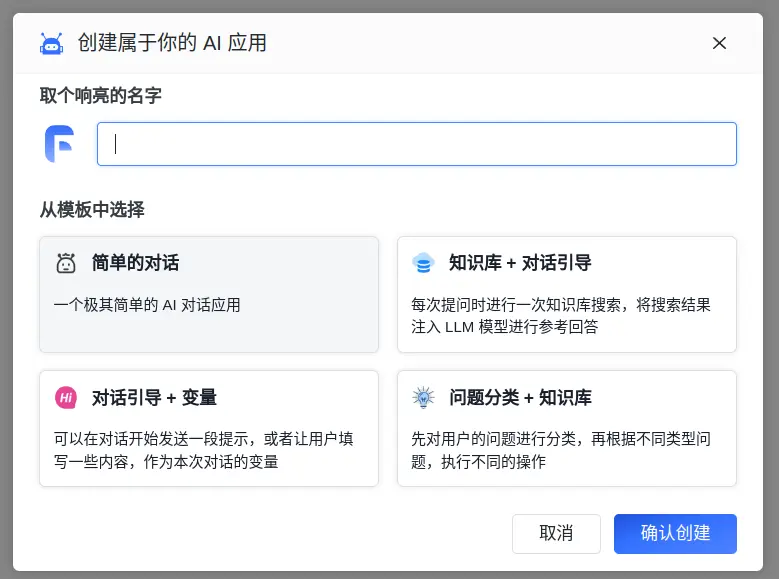
大模型应用_FastGPT
1 功能 整体功能,想解决什么问题 官方说明:FastGPT 是一个基于 LLM 大语言模型的知识库问答系统,提供开箱即用的数据处理、模型调用等能力。同时可以通过 Flow 可视化进行工作流编排,从而实现复杂的问答场景!个人体会…...

elasticsearch|大数据|elasticsearch的api部分实战操作以及用户和密码的管理
一, 前言 本文主要内容是通过elasticsearch的api来进行一些集群的管理和信息查询工作,以及elasticsearch用户的增删改查和密码的重设以及重置如何操作 接上文:elasticsearch|大数据|elasticsearch低版本集群的部署安装和安全增强---密码设…...

Android多进程和跨进程通讯方式
前言 我们经常开发过程中经常会听到线程和进程,在讲述Android进程多进程前我打算先简单梳理一下这俩者。 了解什么是进程与线程 进程: 系统中正在运行的一个应用程序,某个程序一旦运行就是一个进程,是资源分配的最小单位&#…...

通过Jenkins将应用发布到K8s1.24.3
一、准备基础环境 cat >> /etc/hosts <<EOF 192.168.180.210 k8s-master 192.168.180.200 k8s-node1 192.168.180.190 k8s-node2 192.168.180.180 gitlab 192.168.180.170 jenkins 192.168.180.160 harbor EOF 配置主机名 hostnamectl set-hostname k8s-master &am…...

正则表达式入门与实践
文章目录 一、为什么要有正则二、正则表达式基础概念三、Pattern与Matcher类的使用(一)Pattern类的常用方法(二)Matcher类的常用方法四、常用正则规则及其含义(一)规范表示(二)数量表示(三)逻辑运算符五、String对正则表达式的支持六、实践演练(一)匹配给定文本中的…...
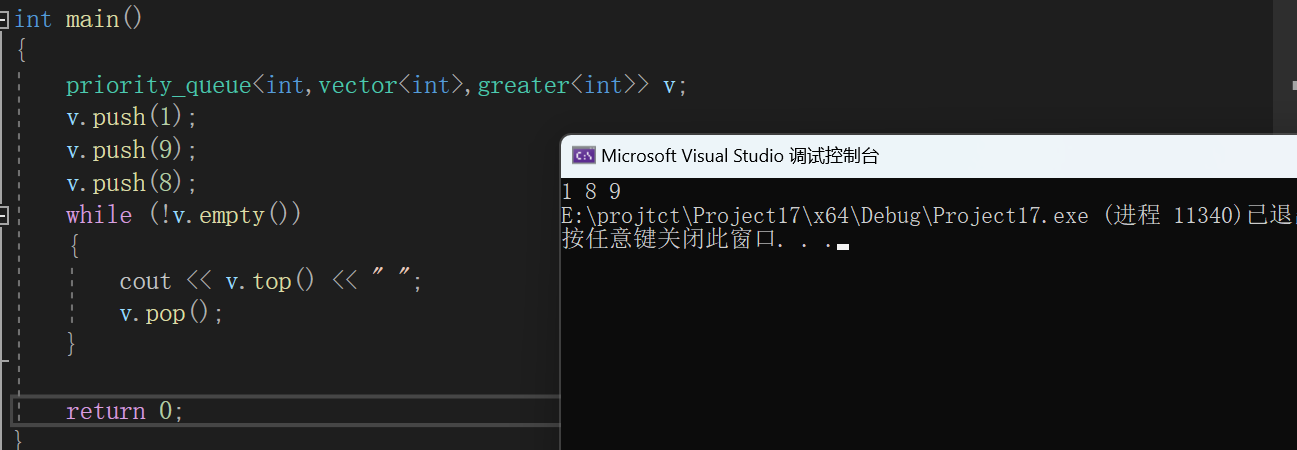
C++初阶(十六)优先级队列
📘北尘_:个人主页 🌎个人专栏:《Linux操作系统》《经典算法试题 》《C》 《数据结构与算法》 ☀️走在路上,不忘来时的初心 文章目录 一、priority_queue的介绍和使用1、priority_queue的介绍2、priority_queue的使用 二、priori…...
深入探索C语言中的二叉树:数据结构之旅
引言 在计算机科学领域,数据结构是基础中的基础。在众多数据结构中,二叉树因其在各种操作中的高效性而脱颖而出。二叉树是一种特殊的树形结构,每个节点最多有两个子节点:左子节点和右子节点。这种结构使得搜索、插入、删除等操作…...

如何发现服务器被入侵了,服务器被入侵了该如何处理?
作为现代社会的重要基础设施之一,服务器的安全性备受关注。服务器被侵入可能导致严重的数据泄露、系统瘫痪等问题,因此及时排查服务器是否被侵入,成为了保障信息安全的重要环节。小德将给大家介绍服务器是否被侵入的排查方案,并采…...
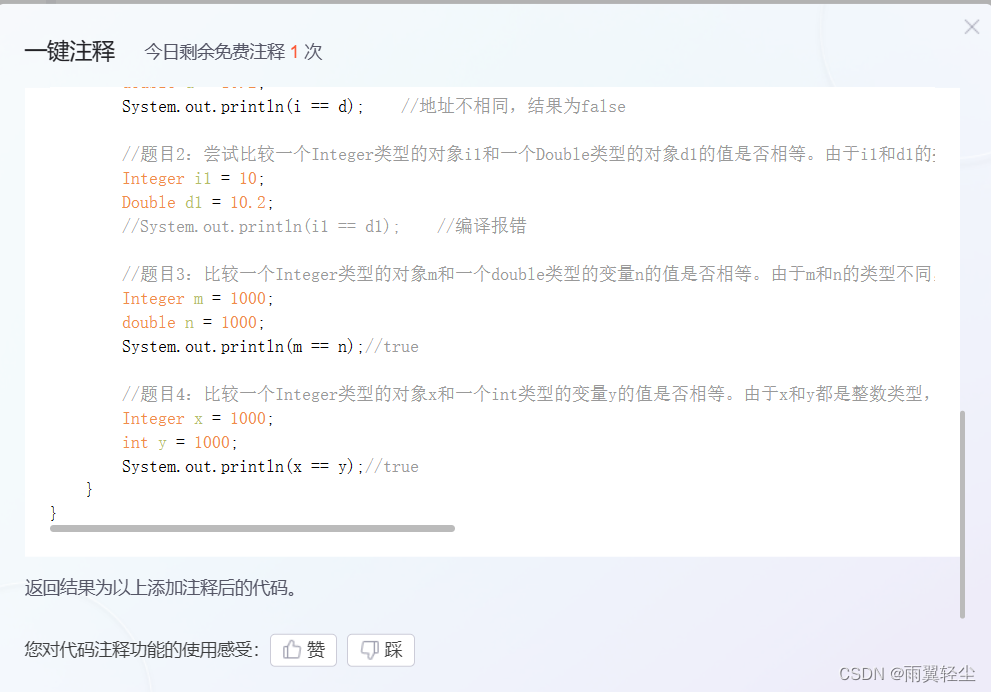
CSDN一键注释功能
这是什么牛逼哄哄的功能 看这里: 然后: 再试一个: 输出结果是?package yuyi03.interview;/*** ClassName: InterviewTest2* Package: yuyi03.interview* Description:** Author 雨翼轻尘* Create 2023/12/14 0014 0:08*/ publ…...
基于JAVA的校园电子商城系统论文
摘 要 网络技术和计算机技术发展至今,已经拥有了深厚的理论基础,并在现实中进行了充分运用,尤其是基于计算机运行的软件更是受到各界的关注。加上现在人们已经步入信息时代,所以对于信息的宣传和管理就很关键。因此校园购物信息的…...
直播传媒公司网站搭建作用如何
直播已然成为抖快等平台的主要生态之一,近些年主播也成为了一种新行业,相关的mcn机构直播传播公司等也时有开业,以旗下主播带来高盈利,而在实际运作中也有一些痛点难题: 1、机构宣传展示难 不少散主播往往会选择合作…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...

WEB3全栈开发——面试专业技能点P4数据库
一、mysql2 原生驱动及其连接机制 概念介绍 mysql2 是 Node.js 环境中广泛使用的 MySQL 客户端库,基于 mysql 库改进而来,具有更好的性能、Promise 支持、流式查询、二进制数据处理能力等。 主要特点: 支持 Promise / async-await…...

渗透实战PortSwigger Labs指南:自定义标签XSS和SVG XSS利用
阻止除自定义标签之外的所有标签 先输入一些标签测试,说是全部标签都被禁了 除了自定义的 自定义<my-tag onmouseoveralert(xss)> <my-tag idx onfocusalert(document.cookie) tabindex1> onfocus 当元素获得焦点时(如通过点击或键盘导航&…...
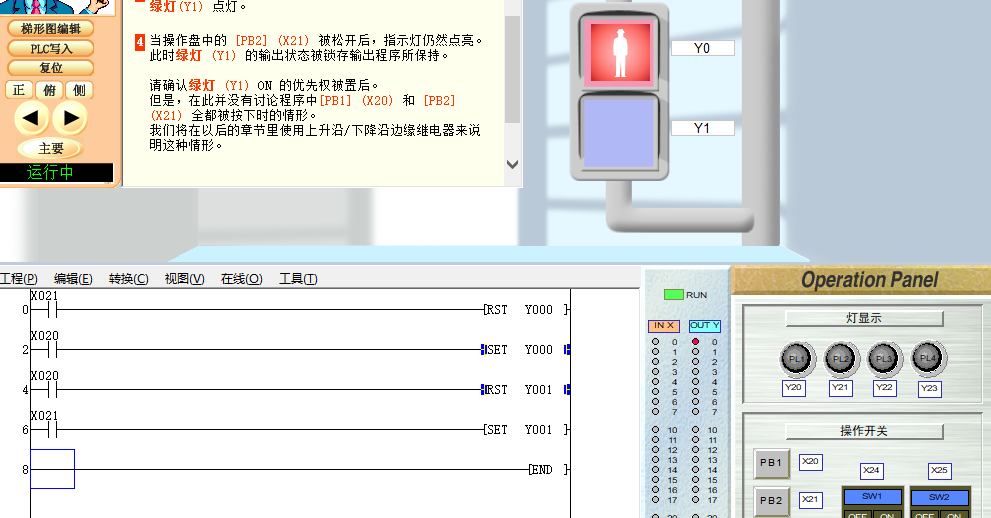
PLC入门【4】基本指令2(SET RST)
04 基本指令2 PLC编程第四课基本指令(2) 1、运用上接课所学的基本指令完成个简单的实例编程。 2、学习SET--置位指令 3、RST--复位指令 打开软件(FX-TRN-BEG-C),从 文件 - 主画面,“B: 让我们学习基本的”- “B-3.控制优先程序”。 点击“梯形图编辑”…...

统计按位或能得到最大值的子集数目
我们先来看题目描述: 给你一个整数数组 nums ,请你找出 nums 子集 按位或 可能得到的 最大值 ,并返回按位或能得到最大值的 不同非空子集的数目 。 如果数组 a 可以由数组 b 删除一些元素(或不删除)得到,…...

Unity VR/MR开发-开发环境准备
视频讲解链接: 【XR马斯维】UnityVR/MR开发环境准备【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...

【RabbitMQ】- Channel和Delivery Tag机制
在 RabbitMQ 的消费者代码中,Channel 和 tag 参数的存在是为了实现消息确认机制(Acknowledgment)和精细化的消息控制。 Channel 参数 作用 Channel 是 AMQP 协议的核心操作接口,通过它可以直接与 RabbitMQ 交互: 手…...
