动态规划(背包问题)
动态规划
文章目录
- 动态规划
- 一、背包问题
- 一、01背包
- 二、完全背包问题
- 三、多重背包问题
- 四、分组背包问题
一、背包问题
一、01背包
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
(1)F[i,j]:只在前i个物品里选,且总体积不超过j的最大价值(2)不选第i个:F[i−1][j](3)选第i个:F[i−1][j−v[i]]+w[i](4)F[i][j]=max(F[i−1][j],F[i−1][j−v[i]]+w[i])\begin{align} &(1)F[i,j]:只在前i个物品里选,且总体积不超过j的最大价值\\ &(2)不选第i个:F[i-1][j]\\ &(3)选第i个 :F[i-1][j-v[i]]+w[i]\\ &(4)F[i][j]=max(F[i-1][j],F[i-1][j-v[i]]+w[i]) \end{align} (1)F[i,j]:只在前i个物品里选,且总体积不超过j的最大价值(2)不选第i个:F[i−1][j](3)选第i个:F[i−1][j−v[i]]+w[i](4)F[i][j]=max(F[i−1][j],F[i−1][j−v[i]]+w[i])
优化前:
memset(f,0,sizeof f);for(int i=1;i<=n;i++)for(int j=0;j<=m;j++){f[i][j]=f[i-1][j]; //不选if(j>=v[i]) f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]); //选}cout<<f[n][m]<<endl;
优化后:(每次只会用到上一层的状态)
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1010;
int n,m;
int f[N];
int v[N],w[N];
int main()
{cin>>n>>m;for(int i=1;i<=n;i++)cin>>v[i]>>w[i];memset(f,0,sizeof f);for(int i=1;i<=n;i++)for(int j=m;j>=v[i];j--){f[j]=max(f[j],f[j-v[i]]+w[i]); //选}cout<<f[m]<<endl;return 0;}
二、完全背包问题
有 N 种物品和一个容量是 V 的背包,每种物品都有无限件可用。
第 i种物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
(1)F[i,j]:只在前i个物品里选,且总体积不超过j的最大价值(2)选k(k>=0)个物品i:F[i−1][j−k∗v[i]]+K∗w[i]\begin{align} &(1)F[i,j]:只在前i个物品里选,且总体积不超过j的最大价值\\ &(2)选k(k>=0)个物品i:F[i-1][j-k*v[i]]+K*w[i]\\ \end{align} (1)F[i,j]:只在前i个物品里选,且总体积不超过j的最大价值(2)选k(k>=0)个物品i:F[i−1][j−k∗v[i]]+K∗w[i]
优化前:
for(int i = 1 ; i<=n ;i++)for(int j = 0 ; j<=m ;j++){for(int k = 0 ; k*v[i]<=j ; k++)f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);}
优化:
f[i , j ] = max( f[i-1,j] , f[i-1,j-v]+w , f[i-1,j-2*v]+2*w , f[i-1,j-3*v]+3*w , .....)
f[i , j-v]= max( f[i-1,j-v] , f[i-1,j-2*v] + w , f[i-1,j-3*v]+2*w , .....)
由上两式,可得出如下递推关系: f[i][j]=max(f[i,j-v]+w , f[i-1][j])
for(int i = 1 ; i <= n ; i++)
for(int j = 0 ; j <= m ; j ++)
{f[i][j] = f[i-1][j];if(j-v[i]>=0)f[i][j] = max(f[i][j],f[i-1][j-v[i]]+w[i]);
}
优化变一维:
for(int i = 1 ; i<=n ;i++)for(int j = v[i] ; j<=m ;j++)//注意了,这里的j是从小到大枚举,和01背包不一样{f[j] = max(f[j],f[j-v[i]]+w[i]);}
三、多重背包问题
有 N 种物品和一个容量是 V 的背包。
第 i 种物品最多有 si 件,每件体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
思路1:参考完全背包
int n,m;
int v[N],w[N],s[N];
int f[N][N];int main()
{cin>>n>>m;for(int i=1;i<=n;i++) cin>>v[i]>>w[i]>>s[i];for(int i=1;i<=n;i++)for(int j=0;j<=m;j++)for(int k=0;k<=s[i]&&k*v[i]<=j;k++)f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);cout<<f[n][m]<<endl;return 0;
}
思路2**:二进制优化将n种物品,每种Si个的多重背包,拆分打包看成N件物品(组)的01背包问题**
(1)例如当s[i]=7时(2)将其拆分为:1,2,4的三组,就可以凑出0−7中的任意数(3)s[i]=9时:1,2,4,2就可以凑出0−7中的任意数\begin{align} &(1)例如当s[i]=7时\\ &(2)将其拆分为:1,2,4的三组,就可以凑出0-7中的任意数\\ &(3)s[i]=9时:1,2,4,2就可以凑出0-7中的任意数 \end{align} (1)例如当s[i]=7时(2)将其拆分为:1,2,4的三组,就可以凑出0−7中的任意数(3)s[i]=9时:1,2,4,2就可以凑出0−7中的任意数
#include<iostream>using namespace std;const int M=12000;int n,m;
int f[M],v[M],w[M];
int main()
{cin>>n>>m;int cnt=0;while(n--){int a,b,c;cin>>a>>b>>c;int t=1;while(c>=t){v[++cnt]=a*t;w[ cnt]=b*t;c-=t;t=t*2;}if(c) {v[++cnt]=a*c; w[cnt]=b*c;}}n=cnt;//转化为了01背包for(int i=1;i<=n;i++)for(int j=m;j>=v[i];j--)f[j]=max(f[j],f[j-v[i]]+w[i]);cout<<f[m]<<endl;return 0;
}
四、分组背包问题
有 N 组物品和一个容量是 V 的背包。
每组物品有若干个,同一组内的物品最多只能选一个。
每件物品的体积是 vij,价值是 wij,其中 i 是组号,j是组内编号。
求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
(1)F[i,j]:只在前i组里选,且总体积不超过j的最大价值(2)不选:F[i−1][j](3)选i组的第k个:F[i−1][j−v[i][k]]+w[i][k]\begin{align} &(1)F[i,j]:只在前i组里选,且总体积不超过j的最大价值\\ &(2)不选:F[i-1][j]\\ &(3)选i组的第k个:F[i-1][j-v[i][k]]+w[i][k] \end{align} (1)F[i,j]:只在前i组里选,且总体积不超过j的最大价值(2)不选:F[i−1][j](3)选i组的第k个:F[i−1][j−v[i][k]]+w[i][k]
#include<iostream>
using namespace std;
const int N=110;
int n,m;
int s[N],v[N][N],w[N][N];
int f[N][N];
int main()
{cin>>n>>m;for(int i=1;i<=n;i++){cin>>s[i];for(int j=0;j<s[i];j++)cin>>v[i][j]>>w[i][j];}for(int i=1;i<=n;i++)for(int j=0;j<=m;j++){f[i][j]=f[i-1][j]; //不选for(int k=0;k<s[i];k++){if(j>=v[i][k]) f[i][j]=max(f[i][j],f[i-1][j-v[i][k]]+w[i][k]); //选第k个}}cout<<f[n][m]<<endl;return 0;
}
相关文章:
)
动态规划(背包问题)
动态规划 文章目录动态规划一、背包问题一、01背包二、完全背包问题三、多重背包问题四、分组背包问题一、背包问题 一、01背包 有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。 第 i 件物品的体积是 vi,价值是 wi。 求解将哪些物品装入背包…...

04741自考计算机网络原理最详细汇总
04741自考计算机网络原理知识点总结 引言 第一章 计算机网络概述 1.计算机网络基本概念与网络结构 1.1 计算机网络的概念; 1.2 计算机网络结构 1.3 数据交换技术 1.4 计算机网络性能 1.5 计算机网络体系结构 1.6 计算机网络与因特网发展简史 第二章 网络应用 2.1 网络应用体系…...
 基本操作)
MySQL 入门学习笔记(二) 基本操作
MySQL 入门学习笔记(二) 数据库和表的基本操作 我们把一些表的集合称之为数据库,一个服务器中可以存在多个数据库.每个数据库中包含多个表,每个表都有一个名字作为标识,数据表则包含带有数据的记录. PS:SQL 语句对大小写不敏感. 操作数据库命令 在 MySQL 命令中,数据库用DAT…...
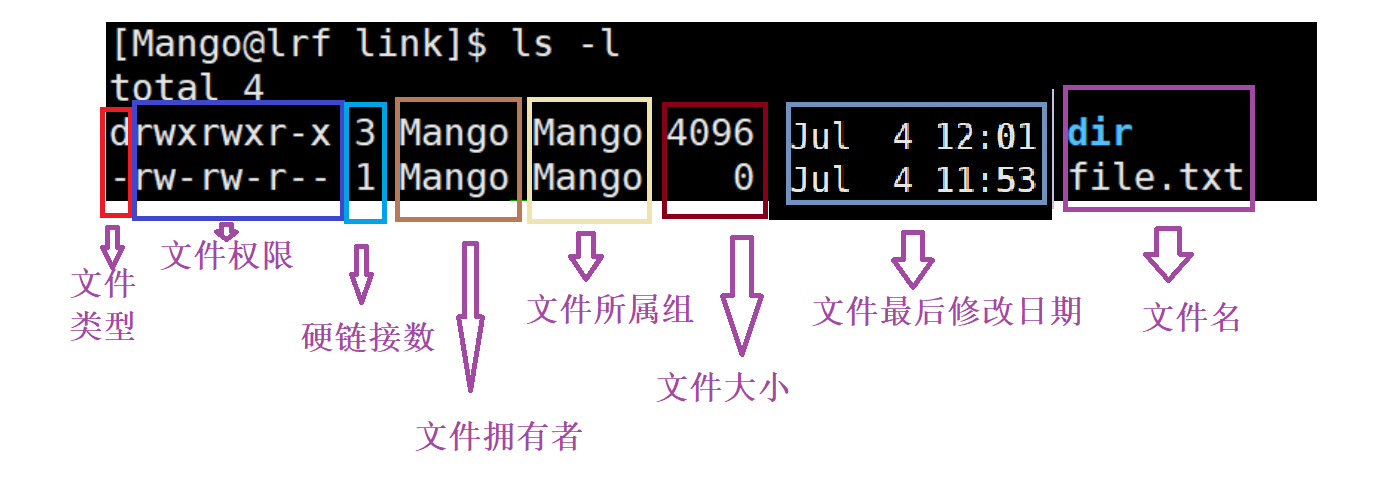
【Linux】理解文件系统
文章目录理解文件系统了解磁盘结构inode理解文件系统 了解磁盘结构 磁盘是计算机中的一个 机械设备 这个磁盘的盘片就像光盘一样,数据就在盘片上放着, 但是光盘是只读的,磁盘是可读可写的 机械硬盘的寻址的工作方式: 盘片不断旋转,磁头不断摆动,定位到特定的位置 我们可以把…...

Java如何String字符串带括号转成List
问题现象 今天在做一个需求:将存入数据库中的数据读到后解析成list遍历分析 数据格式: "[1677660600000, 1677660900000, 1677661200000]" "[5, 4, 4,3,2,0,0]" 我一开始想到的就是使用逗号分割即可 结果变成了这样的…...

react 使用 mqtt
也许很多人都好奇这个mqtt是什么东西,其实在互联网上可能不会使用到它,它是物联网上的东西,也是一种通信协议跟websocket。但它也能在浏览器跟服务器上跑,它的底层实现也是封装了websocket。 MQTT MQTT是一个客户端服务端架构的发…...

W25Q256被写保护如何修改
W25Q256被写保护如何修改1、 W25Q256数据读不到1.1 打印的寄存器的值1.2 可能原因1.3 解决办法1.4 用到的函数1、 W25Q256数据读不到 能够正确的读到ID,但是读到的数据不正确 1.1 打印的寄存器的值 0x2 BUSY :只读, 指令正在执行 WEL (1) &…...

论文投稿指南——中文核心期刊推荐(中国文学作品)
【前言】 🚀 想发论文怎么办?手把手教你论文如何投稿!那么,首先要搞懂投稿目标——论文期刊 🎄 在期刊论文的分布中,存在一种普遍现象:即对于某一特定的学科或专业来说,少数期刊所含…...

MySQL 问题总结
什么是MVCC? 说说MySQL实现MVCC的原理? MVCC,全称Multi-Version Concurrency Control,即多版本并发控制。MVCC是一种并发控制的方法,一般在数据库管理系统中,实现对数据库的并发访问。 对于「读已提交」和…...
62. 不同路径
62. 不同路径 一个机器人位于一个 m∗nm * nm∗n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。 问总共有多少条不同的路…...
在windows安装python3.11同时进行一个数据的练习
安装包百度网盘如下: 链接:https://pan.baidu.com/s/1l9H1GWP64LOxLaXXLie2uA?pwd6666 提取码:6666 1.我们选择自定义安装 2.当我们点了自定义安装后就直接next 3.修改路径,之后点击安装(install) 4.安装完成,进行…...

Java接口专题
基本介绍 接口给出一些没有实现的方法,封装到一起,到某个类使用时再根据具体情况把这些方法写出来。 注意:在jdk7之前,接口里所有的方法都是抽象方法。在jdk8之后接口中可以有静态方法,默认方法 interface 接口名{/…...

6招优化WordPress打开速度-让你的网站飞起来
为什么我们的WordPress网站比你的快? 我们的官网是使用WordPress框架搭建的,有没有发现我们的网站非常快,而你的WordPress网站比较慢呢?那是因为我们的网站经过了优化。 WordPress 很慢? 为什么很多人都会觉得 Word…...

春天到了,来一场 VoxEdit 创作大赛吧!
春天的气息扑面而来,这是让你尽情绽放创造力的最佳时机!我们将以「春天」为主题来一场 VoxEdit 大赛。在这里,你可以展示你的才华并赢得 $SAND 奖励! 无论你是专业的设计师,还是仅仅喜欢创造美丽的艺术,这场…...
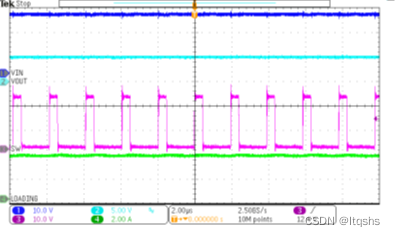
异步Buck和同步Buck的特点
1 介绍 随着时代的发展,工业,车载,通信,消费类等产品都提出了小型化,智能化的需求。相应的,对于这些系统中的电源模块提出了小型化的要求。目前,市场上依然存在很多异步Buck电源管理芯片使用的场…...
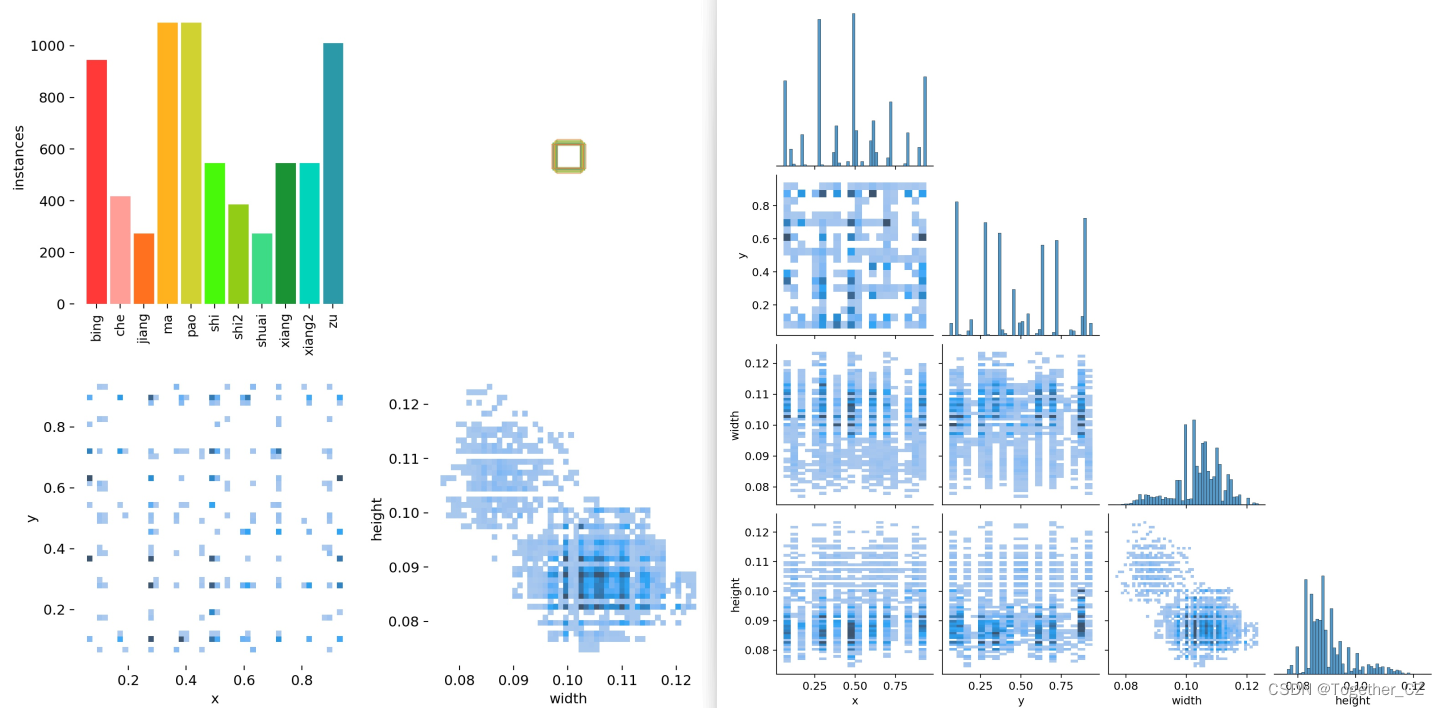
基于轻量级YOLO开发构建中国象棋目标检测识别分析系统
关于棋类相关的项目在我之前的博文里面都有做过,如下:《yolov5s融合SPD-Conv用于提升小目标和低分辨率图像检测性能实践五子棋检测识别》《YOLOV5融合SE注意力机制和SwinTransformer模块开发实践的中国象棋检测识别分析系统》《基于yolov5s实践国际象棋目…...

机器学习100天(三十五):035 贝叶斯公式
《机器学习100天》完整目录:目录 机器学习100天,今天讲的是:贝叶斯公式! 好了,上一节介绍完先验概率、后验概率、联合概率、全概率后,我们来看这样一个问题:如果我现在挑到了一个瓜蒂脱落的瓜,则该瓜是好瓜的概率多大? 显然,这是一个计算后验概率的问题,根据我们之…...

大话数据结构-栈
1 概述 栈(Stack)是限定仅在表尾进行插入和删除操作的线性表。 允许插入和删除的一端称为栈顶(top),另一端称为栈底(bottom),不含任何数据元素的栈称为空栈,栈又称为后进…...

javaFx实现放大镜效果——圆形、矩形、三角形放大镜,拖动调整放大镜大小,设置放大倍数
系列文章专栏:javafx图形绘制、桌面录屏录音源码合集 目录 一、实现的效果 二、实现思路 三、程序实现...

什么是客户忠诚度?建立忠诚文化的 5 种方法
客户忠诚度影响企业的各个方面,例如收入、品牌形象、预算分配和产品路线图。拥有忠实的客户群对于建立成功的企业至关重要,因为您的客户是您的主要拥护者,有助于为您的企业营造积极的氛围。 什么是客户忠诚度? 客户忠诚度衡量客户…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...
