当前位置： 首页 > news >正文

矩阵理论及其应用邱启荣习题3.5题解

news 2026/2/11 0:59:54

(1) P= ( − 1 0 1 − 1 − 1 2 1 1 − 1 ) \begin{pmatrix} -1 & 0&1 \\ -1 & -1&2\\1&1&-1 \end{pmatrix} ​−1−11​0−11​12−1​ ​
A= ( 1 0 1 1 1 0 − 1 2 1 ) \begin{pmatrix} 1 & 0&1 \\ 1 & 1&0\\-1&2&1 \end{pmatrix} ​11−1​012​101​ ​
B=P − 1 ^{-1} −1AP= ( − 2 − 3 5 0 0 2 − 2 − 2 5 ) \begin{pmatrix} -2 & -3&5 \\ 0 & 0&2\\-2&-2&5 \end{pmatrix} ​−20−2​−30−2​525​ ​
( 2 ) T ( α ) = T ( α 1 ) + 6 T ( α 2 ) − T ( α 3 ) = ( 1 , 0 , 1 ) + ( 6 , 6 , 0 ) + ( 1 , − 2 , − 1 ) = ( 8 , 4 , 0 ) \begin{aligned}(2)\space T(\alpha)&=T(\alpha_1)+6T(\alpha_2)-T(\alpha_3)\\&=(1,0,1)+(6,6,0)+(1,-2,-1)\\&=(8,4,0) \end{aligned} (2) T(α)​=T(α1​)+6T(α2​)−T(α3​)=(1,0,1)+(6,6,0)+(1,−2,−1)=(8,4,0)​
T ( β ) = T ( e 1 ) − T ( e 2 ) + T ( e 3 ) = ( − 2 , − 3 , 5 ) + ( 0 , 0 , − 2 ) + ( − 2 , − 2 , 5 ) = ( − 4 , − 5 , 8 ) \begin{aligned}T(\beta)&=T(e_1)-T(e_2)+T(e_3)\\&=(-2,-3,5)+(0,0,-2)+(-2,-2,5)\\&=(-4,-5,8) \end{aligned} T(β)​=T(e1​)−T(e2​)+T(e3​)=(−2,−3,5)+(0,0,−2)+(−2,−2,5)=(−4,−5,8)​
注意 α \alpha α是行向量

相关文章：

矩阵理论及其应用邱启荣习题3.5题解

(1) P ( − 1 0 1 − 1 − 1 2 1 1 − 1 ) \begin{pmatrix} -1 & 0&1 \\ -1 & -1&2\\1&1&-1 \end{pmatrix} ​−1−11​0−11​12−1​ ​ A ( 1 0 1 1 1 0 − 1 2 1 ) \begin{pmatrix} 1 & 0&1 \\ 1 & 1&0\\-1&2&1 \end{pmat…...

编程日记 2023/12/16 5:04:59

Java面试题（每天10题）-------连载（49）

目录 Tomcat篇 1、Tomcat的缺省端口是多少？怎么修改？ 2、Tomcat有哪几种Connector运行模式（优化）？ 3、Tomcat有几种部署方式？ 4、Tomcat容器时如何创建servlet类实例？用到了什么原理&…...

编程日记 2023/12/16 5:03:58

python——数据类型

数据类型目录 前言一、Number（数字）数字类型转换：二、String（字符串）常用字符串运算符：字符串格式化：三、Tuple（元组）常用运算符四、List（列表）嵌套列表：常用列表操作：五、Dictionary（字典）六、Set（集合）...

编程日记 2023/12/16 5:01:57

hive中如何求取中位数？

目录 中位数的概念代码实现准备数据实现 中位数的概念 中位数（Median）又称中值，统计学中的专有名词，是按顺序排列的一组数据中居于中间位置的数，代表一个样本、种群或概率分布中的一个数值，其可将数值集合…...

编程日记 2023/12/16 5:00:55

在C#中异步编程

在C#中，异步编程是一种编写并发和响应式代码的技术，通过将耗时的操作放在后台线程中执行，以避免阻塞主线程，提高程序的性能和响应性。异步编程使用async和await关键字，结合任务（Task）和异步操作…...

编程日记 2023/12/16 4:59:54

微服务保护--Feign整合Sentinel

限流是一种预防措施，虽然限流可以尽量避免因高并发而引起的服务故障，但服务还会因为其它原因而故障。而要将这些故障控制在一定范围，避免雪崩，就要靠线程隔离（舱壁模式）和熔断降级手段了。 线程隔离之前讲到…...

编程日记 2023/12/16 4:58:54

二进制to十六进制

输入小于等于十六位的二进制数据&#xff0c;输出十六进制数据&#xff1b; #include <stdio.h> #include <stdlib.h> #include <math.h>int main(void) {char arr[16] { 0 }; int array[16] { 0 }; int hex[4] { 0 };int i 0; int num 0;scanf("…...

编程日记 2023/12/16 4:57:53

Logistic 回归算法

Logistic 回归 Logistic 回归算法Logistic 回归简述Sigmoid 函数Logistic 回归模型表达式求解参数 $\theta $梯度上升优化算法 Logistic 回归简单实现使用 sklearn 构建 Logistic 回归分类器Logistic 回归算法的优缺点 Logistic 回归算法 Logistic 回归简述 Logistic 回归是一…...

编程日记 2023/12/16 4:56:52

ubuntu安装详细步骤

一&#xff0c;先下载vmware 1&#xff0c;第一步打开上面链接 下载网址 : https://www.vmware.com/products/workstation-pro/wo rkstation-pro-evaluation.html 许可证 JU090-6039P-08409-8J0QH-2YR7F ZF3R0-FHED2-M80TY-8QYGC-NPKYF FC7D0-D1YDL-M8DXZ-CYPZE-P2AY6 ZC3T…...

编程日记 2023/12/16 4:54:50

力扣5. 最长回文子串

动态规划 思路&#xff1a; 假设 dp[i][j] 为字符串 (i, j) 子串是否为回文的结果&#xff1b;那么 dp[i][j] dp[i 1][j - 1] 且 (s[i] s[j])&#xff1b;长度为1的字符串都是回文&#xff1b; 原字符串长度为1&#xff0c;是回文&#xff1b;原字符串子串长度为1&#xff…...

编程日记 2023/12/16 4:53:49

肆[4]，函数VectorToHomMat2d/AffineTransPoint2d

函数VectorToHomMat2d C形式 LIntExport void VectorToHomMat2d( const HTuple& Px, const HTuple& Py, const HTuple& Qx, const HTuple& Qy, HTuple* HomMat2D);//参数1:图像坐标X数组 //参数2:图像坐标Y数组 //参数3:世界坐标X数组 //参数4:世界坐标Y…...

编程日记 2023/12/16 4:52:48

下载文件 后端返回给前端 response header 响应头

当浏览器在请求资源时&#xff0c;会通过http返回头中的content-type决定如何显示/处理将要加载的数据&#xff0c;如果这个类型浏览器能够支持阅览&#xff0c;浏览器就会直接展示该资源&#xff0c;比如png、jpeg、video等格式。在某些下载文件的场景中&#xff0c;服务端可能…...

编程日记 2023/12/16 4:51:47

lvs负载均集群

目录 NAT模式 LVS负载均衡群集部署 1.部署共享存储 2.配置节点服务器 192.168.17.130 ​编辑 192.168.17.133 3.配置负载调度器 4.测试效果 NAT模式 LVS负载均衡群集部署 负载调度器&#xff1a;内网关 ens33&#xff1a;192.168.17.70&#xff0c;外网关 ens36&#x…...

编程日记 2023/12/16 4:50:46

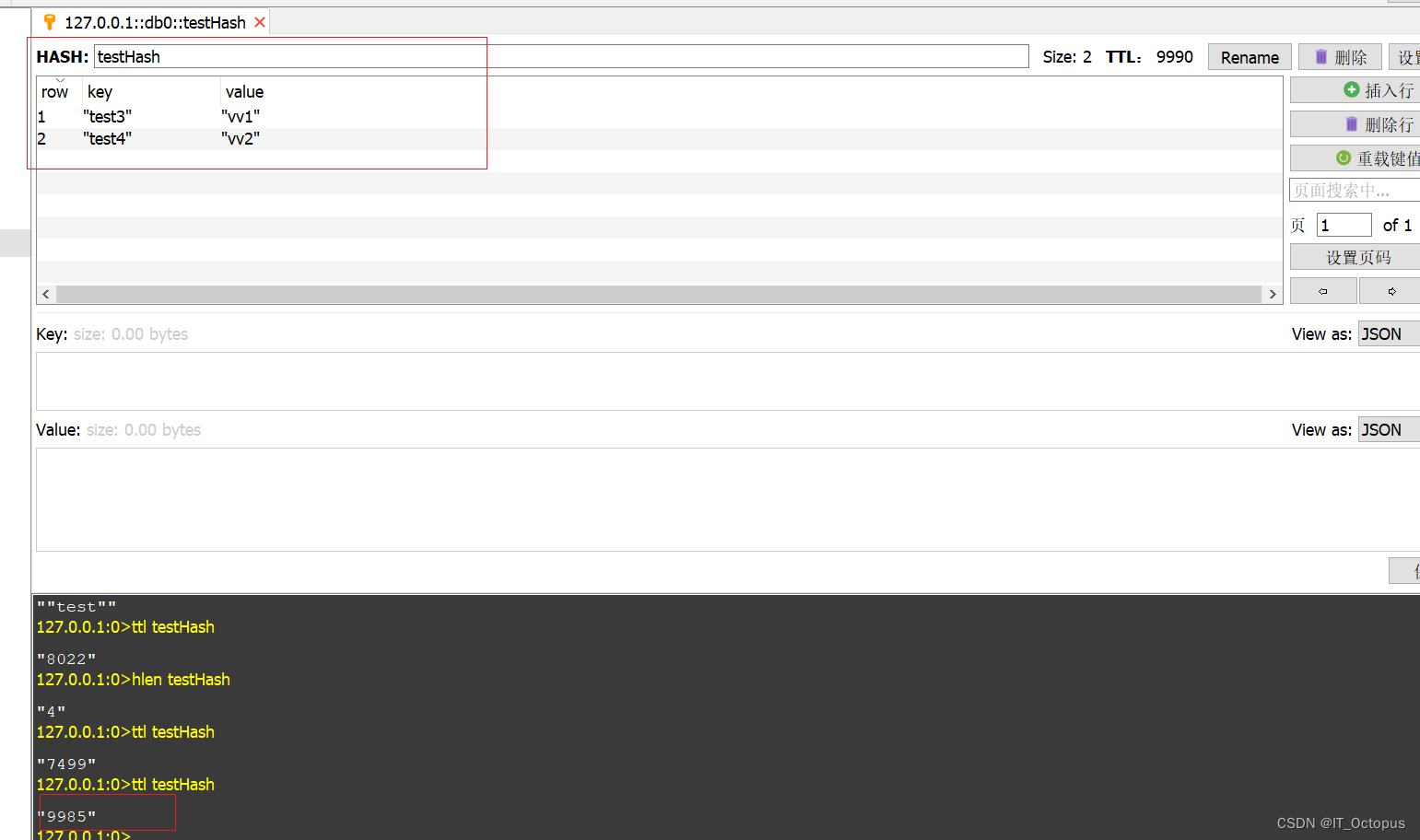
luttuce(RedisTempate)实现hash expire lua脚本

话不多说先放脚本&#xff1a; local argv ARGV local length #argv if length > 0 then local unpackArgs {} for i 1, length - 1 dotable.insert(unpackArgs, argv[i]) end if redis.call(exists, KEYS[1]) 1 thenredis.call(del, KEYS[1])redis.call(hset, KEYS[…...

编程日记 2023/12/16 4:49:45

【Xamarin】WebView连接局域网自动跳转外部浏览器问题的解决

xamarin在中国用的很少&#xff0c;但也有一些独到之处。例如用惯了Visual Studio的就很合适。而且类Java开发&#xff0c;几乎没什么障碍。 protected override void OnCreate(Bundle savedInstanceState) {base.OnCreate(savedInstanceState);Xamarin.Essentials.Platform.I…...

编程日记 2023/12/16 4:48:44

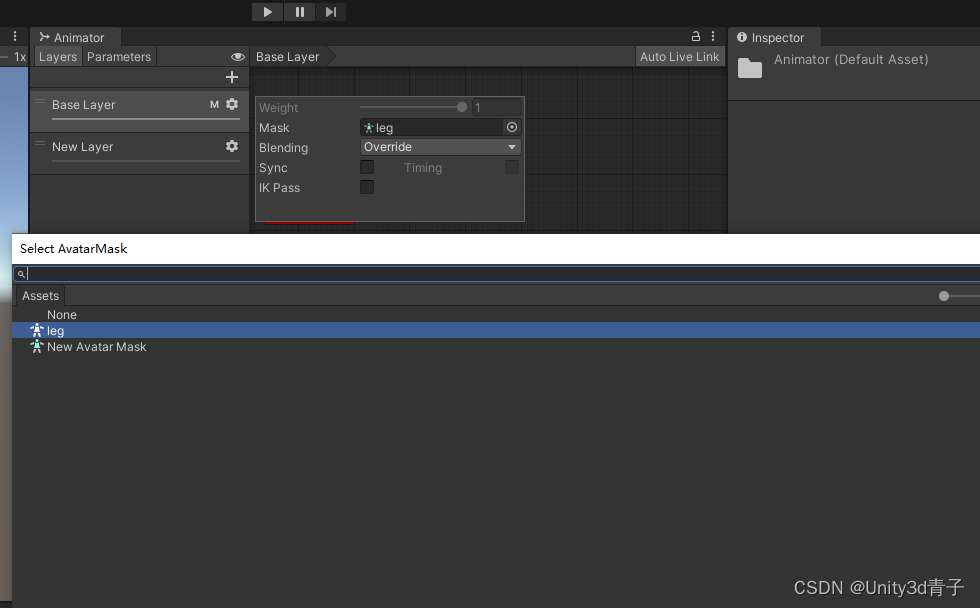
【Unity动画】实现不同的肢体动作自由搭配播放Layer+Avatar Mask

这个教程教你学会使用Unity 动画层配合布偶遮罩&#xff08;AvaterMask&#xff09; 实现从2个动画身上只保留部分肢体动作&#xff0c;然后搭配播放 例如&#xff1a;一个正常跑的动画片段&#xff0c;我只保留腿部动作&#xff0c;形成一个层叫Run_leg 然后在从一个攻击动作…...

编程日记 2023/12/16 4:43:39

将0x06（16进制）转换为二进制

将0x06&#xff08;16进制&#xff09;转换为二进制&#xff0c;可以按照如下步骤进行&#xff1a; 1. 将0x06中的字母"0x"去除。 2. 将数字"06"中的数字"0"去除。 3. 将数字"06"转换为二进制。 根据步骤1和步骤2&#xff0c;去除&q…...

编程日记 2023/12/16 4:41:38

考PRINCE2有用么？有PMP证书了还需要考PRINCE2吗？

有用的&#xff0c;PMP相当于是理论&#xff0c;PRINCE2是实践&#xff0c;对小白来说pmp考后再考一个prince2是很好的选择&#xff0c;对项目管理的小白来说更好入门。 先来说下 prince 2 和 pmp 的区别 一、prince 2 是什么&#xff1f;跟PMP有什么区别&#xff1f; prince…...

编程日记 2023/12/16 4:38:35

06进程间关系-学习笔记

Orphan Process孤儿进程 父进程先于子进程退出&#xff0c;子进程失去托管&#xff0c;这种子进程统称为孤儿进程 失效进程&#xff08;孤儿进程&#xff09;&#xff1a;导致内存泄漏&#xff0c;影响新进程的创建孤儿进程的危害不可预测&#xff0c;如果一个孤儿进程持续的申…...

编程日记 2023/12/16 4:34:32

Vue的动画方式有几种

Vue的动画方式有几种&#xff1f; Vue的动画方式主要分成两大类&#xff0c;一类是CSS动画&#xff0c;一类是JS动画 CSS动画中包含transition以及animation&#xff0c;但在Vue中只需要通过transition封装组件实现。 CSS动画的类名主要包括&#xff1a;v-enter、v-enter-acti…...

编程日记 2023/12/16 4:31:28

龙虎榜——20250610

上证指数放量收阴线&#xff0c;个股多数下跌&#xff0c;盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型&#xff0c;指数短线有调整的需求&#xff0c;大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的&#xff1a;御银股份、雄帝科技 驱动…...

编程新知 2026/2/10 23:39:36

论文解读：交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架（二）

HoST框架核心实现方法详解 - 论文深度解读（第二部分） 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章： 论文深度解读 + 算法与代码分析（二） 作者机构： 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题： 人形机器人…...

编程新知 2026/2/9 0:12:12

Zustand 状态管理库：极简而强大的解决方案

Zustand 是一个轻量级、快速和可扩展的状态管理库&#xff0c;特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

编程新知 2026/2/8 10:56:57

以下是对华为 HarmonyOS NETX 5属性动画（ArkTS）文档的结构化整理，通过层级标题、表格和代码块提升可读性：

一、属性动画概述NETX 作用&#xff1a;实现组件通用属性的渐变过渡效果&#xff0c;提升用户体验。支持属性&#xff1a;width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项&#xff1a; 布局类属性&#xff08;如宽高&#xff09;变化时&#…...

编程新知 2026/1/28 21:15:38

渗透实战PortSwigger靶场-XSS Lab 14：大多数标签和属性被阻止

<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet&#xff1a; https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

编程新知 2026/1/24 13:05:24

postgresql|数据库|只读用户的创建和删除（备忘）

CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

编程新知 2025/9/18 19:34:22

使用van-uploader 的UI组件，结合vue2如何实现图片上传组件的封装

以下是基于 vant-ui&#xff08;适配 Vue2 版本 &#xff09;实现截图中照片上传预览、删除功能&#xff0c;并封装成可复用组件的完整代码&#xff0c;包含样式和逻辑实现&#xff0c;可直接在 Vue2 项目中使用&#xff1a; 1. 封装的图片上传组件 ImageUploader.vue <te…...

编程新知 2026/1/31 2:37:22

CocosCreator 之 JavaScript/TypeScript和Java的相互交互

引擎版本&#xff1a; 3.8.1 语言&#xff1a; JavaScript/TypeScript、C、Java 环境&#xff1a;Window 参考&#xff1a;Java原生反射机制 您好&#xff0c;我是鹤九日&#xff01; 回顾 在上篇文章中&#xff1a;CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

编程新知 2026/1/30 12:10:19

C# 类和继承(抽象类)

抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

编程新知 2026/1/29 16:25:24

ArcGIS Pro制作水平横向图例+多级标注

今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作&#xff1a;ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等&#xff08;ArcGIS出图图例8大技巧&#xff09;&#xff0c;那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

编程新知 2026/2/4 17:18:03