当前位置： 首页 > news >正文

金蝶云星空协同开发环境应用内执行单据类型脚本

news 2026/2/11 0:41:35

文章目录

  • 金蝶云星空协同开发环境应用内执行单据类型脚本
    • 业务界面
    • 查询单据类型表数据
    • 导出数据
    • 执行数据库脚本
    • 单据类型xml
    • 检验是否执行成功
      • 检查数据库
      • 检查业务数据

金蝶云星空协同开发环境应用内执行单据类型脚本

业务界面

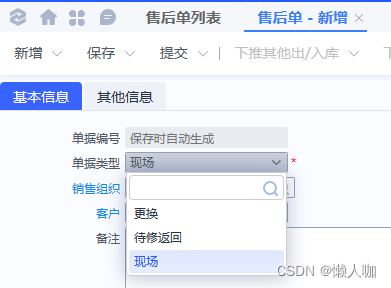
在这里插入图片描述

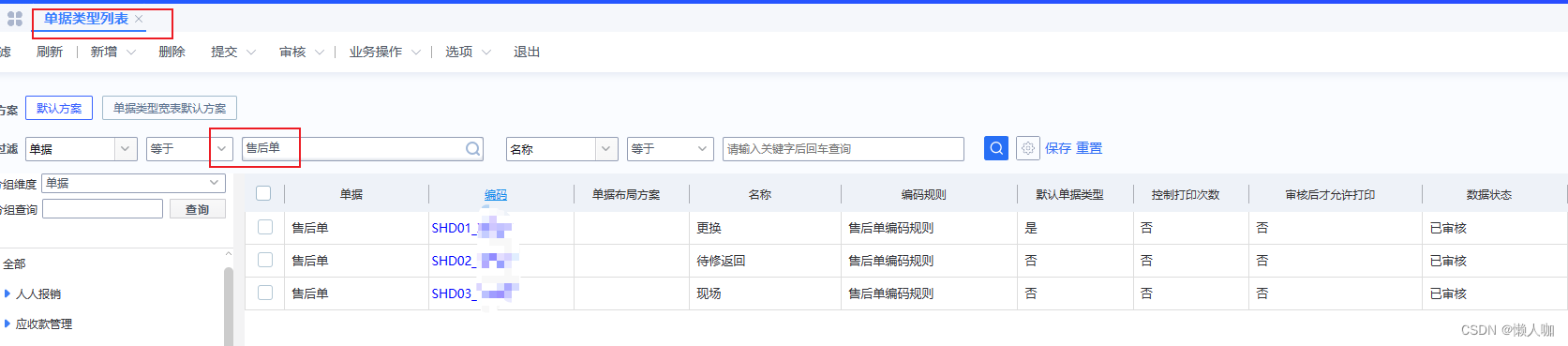
查询单据类型表数据

先使用类型中文在单据类型多语言表T_BAS_BILLTYPE_L找到主键后再查询单据类型主表T_BAS_BILLTYPE

SELECT * FROM T_BAS_BILLTYPE_L WHERE FNAME='现场'
SELECT * FROM T_BAS_BILLTYPE  WHERE FBILLTYPEID='64f7fa60387282'

导出数据

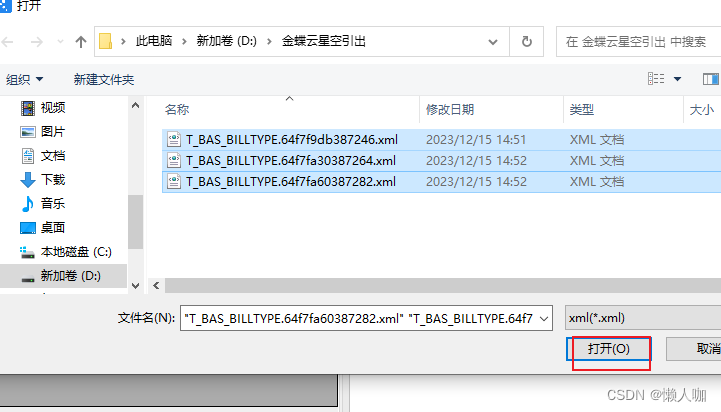
登录需要导出数据的账套的BOS开发平台
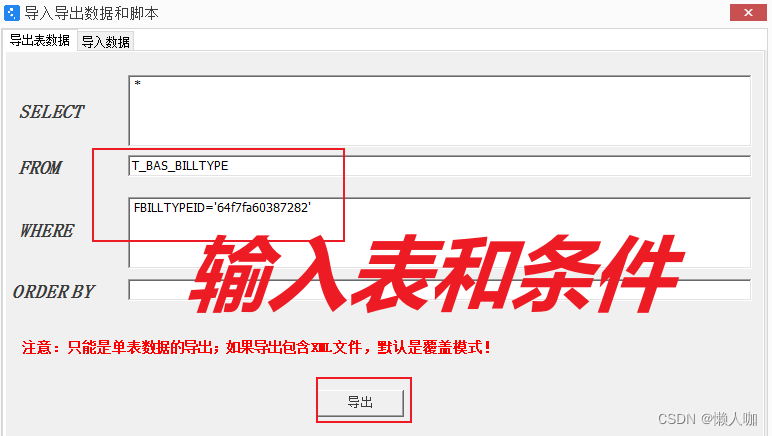
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
输入表和条件，然后执行导出。
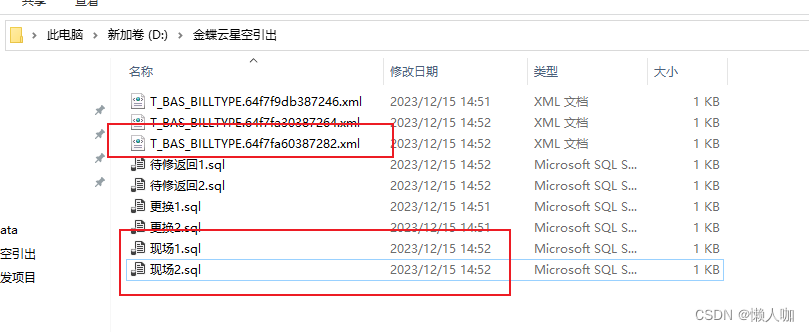
导出后如图，两个表数据和一个xml。
在这里插入图片描述

执行数据库脚本

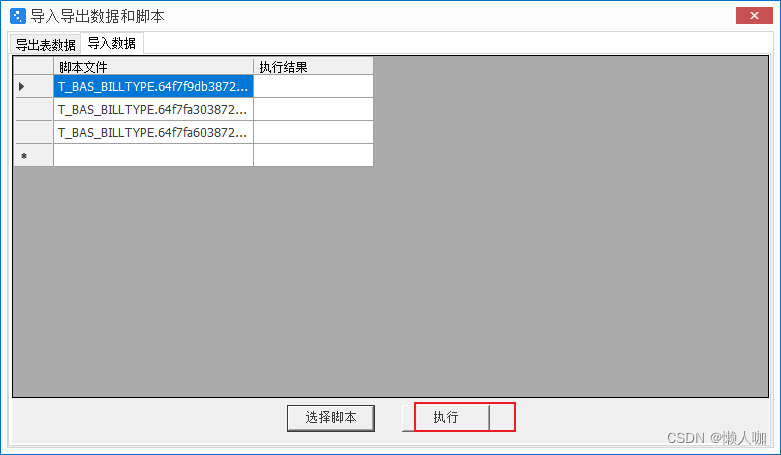
登录需要引入数据的BOS平台。

然后打开导入导出数据和脚本的界面。

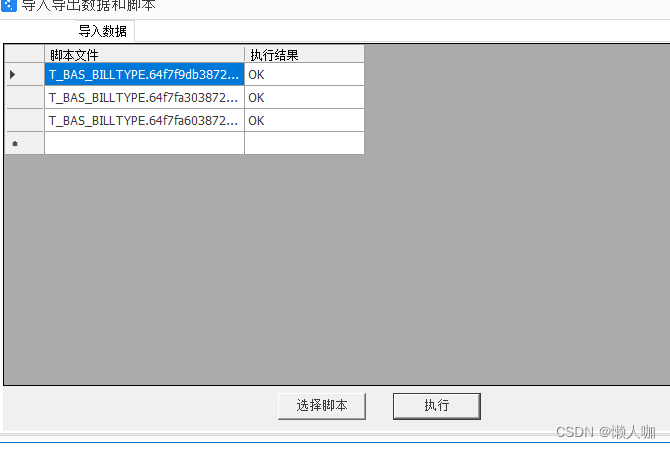
选择需要执行的脚本，进行执行。
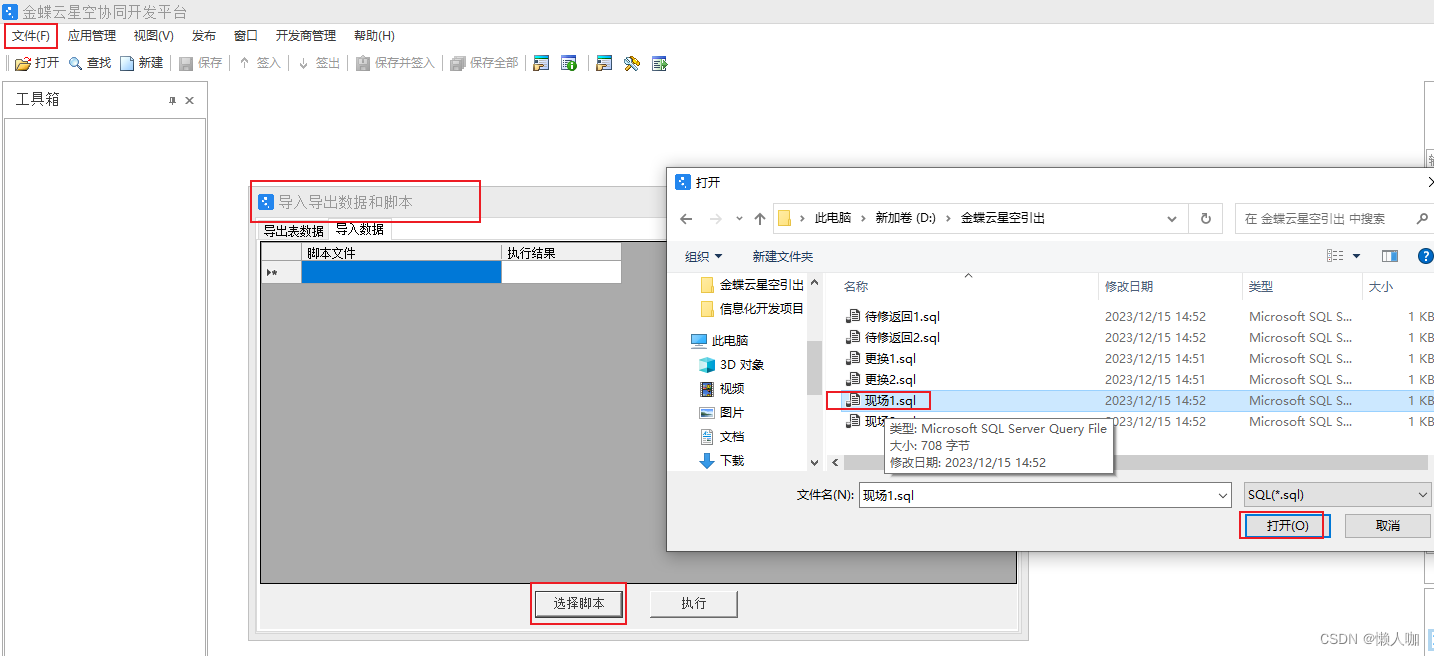
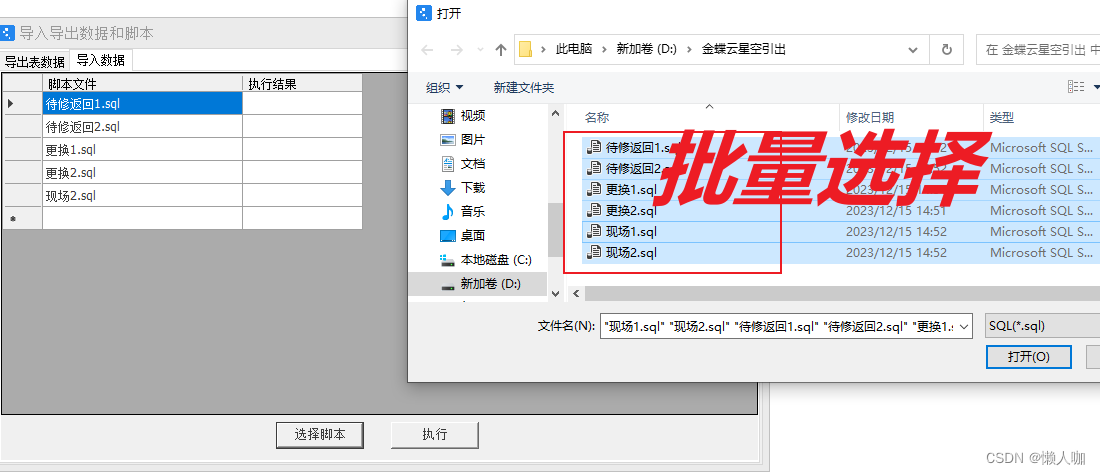
在这里插入图片描述

也可以批量选择。
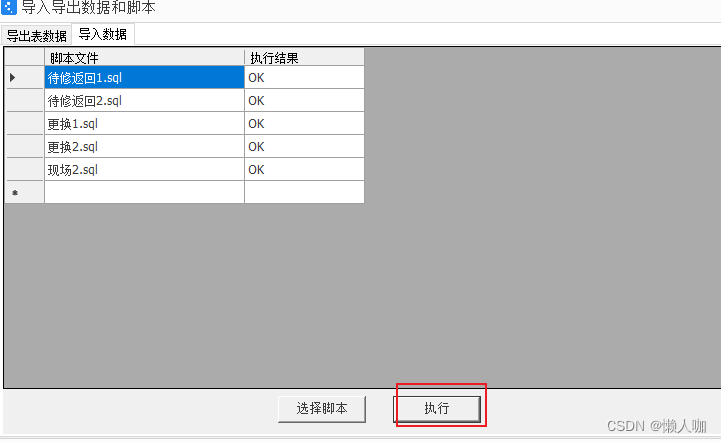
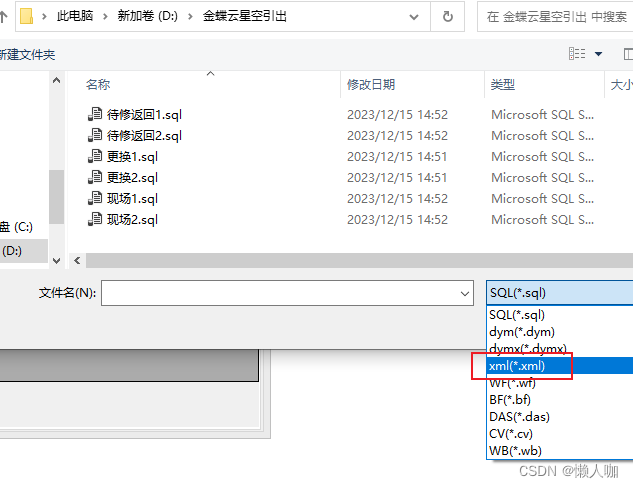
在这里插入图片描述
在这里插入图片描述

单据类型xml

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

检验是否执行成功

检查数据库

SELECT * FROM T_BAS_BILLTYPE  WHERE FBILLTYPEID='64f7f9db387246'
SELECT * FROM T_BAS_BILLTYPE_L WHERE FNAME='更换'SELECT * FROM T_BAS_BILLTYPE  WHERE FBILLTYPEID='64f7fa30387264'
SELECT * FROM T_BAS_BILLTYPE_L WHERE FNAME='待修返回'--先使用类型中文在单据类型多语言表T_BAS_BILLTYPE_L找到主键后再查询单据类型主表T_BAS_BILLTYPE
SELECT * FROM T_BAS_BILLTYPE  WHERE FBILLTYPEID='64f7fa60387282'SELECT * FROM T_BAS_BILLTYPE_L WHERE FNAME='现场'

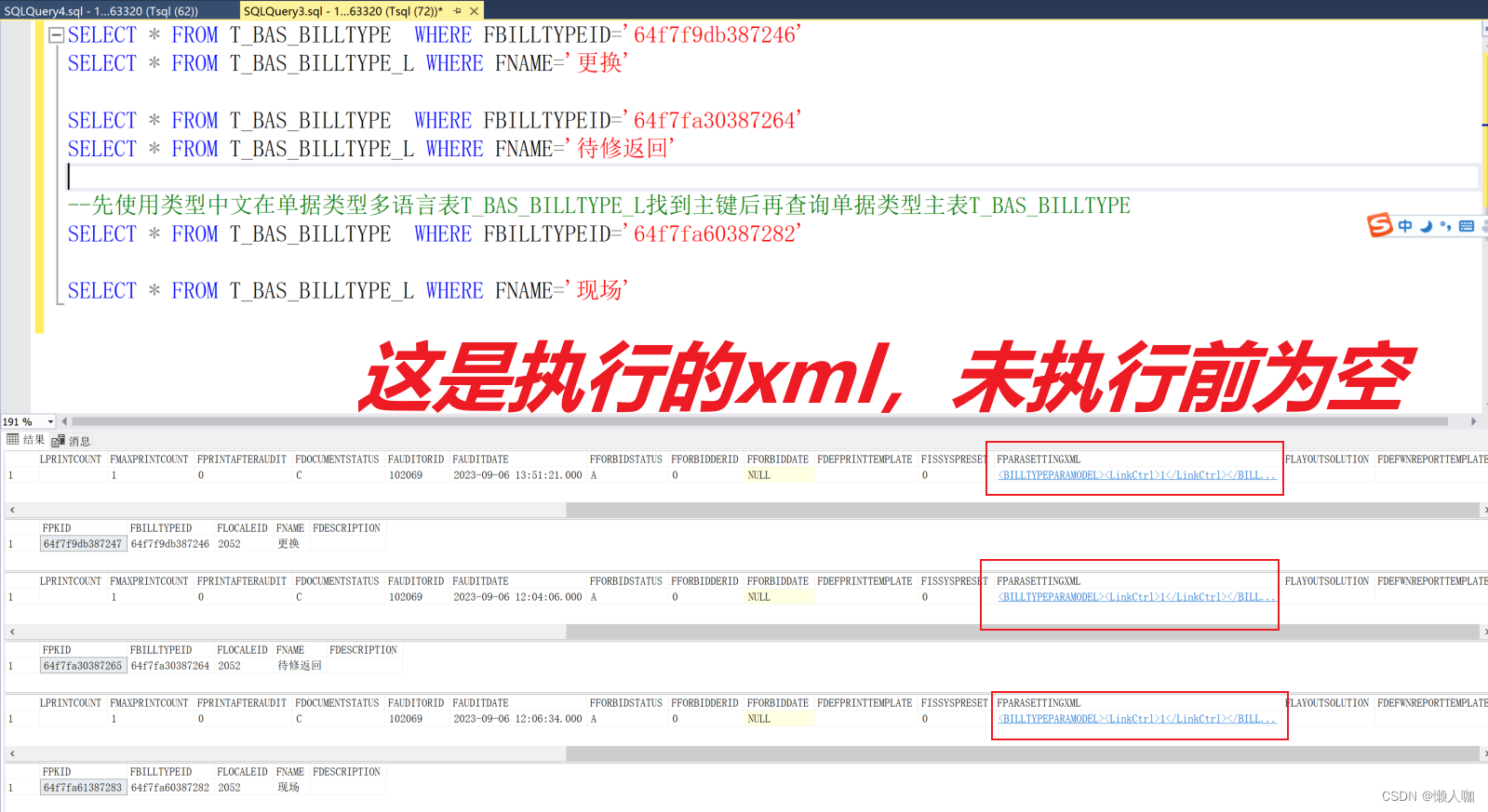
在这里插入图片描述

检查业务数据

在这里插入图片描述

相关文章：

金蝶云星空协同开发环境应用内执行单据类型脚本

文章目录 金蝶云星空协同开发环境应用内执行单据类型脚本业务界面查询单据类型表数据导出数据执行数据库脚本单据类型xml检验是否执行成功检查数据库检查业务数据 金蝶云星空协同开发环境应用内执行单据类型脚本 业务界面 查询单据类型表数据 先使用类型中文在单据类型多语言…...

编程日记 2023/12/16 5:07:00

矩阵理论及其应用邱启荣习题3.5题解

(1) P ( − 1 0 1 − 1 − 1 2 1 1 − 1 ) \begin{pmatrix} -1 & 0&1 \\ -1 & -1&2\\1&1&-1 \end{pmatrix} ​−1−11​0−11​12−1​ ​ A ( 1 0 1 1 1 0 − 1 2 1 ) \begin{pmatrix} 1 & 0&1 \\ 1 & 1&0\\-1&2&1 \end{pmat…...

编程日记 2023/12/16 5:04:59

Java面试题（每天10题）-------连载（49）

目录 Tomcat篇 1、Tomcat的缺省端口是多少？怎么修改？ 2、Tomcat有哪几种Connector运行模式（优化）？ 3、Tomcat有几种部署方式？ 4、Tomcat容器时如何创建servlet类实例？用到了什么原理&…...

编程日记 2023/12/16 5:03:58

python——数据类型

数据类型目录 前言一、Number（数字）数字类型转换：二、String（字符串）常用字符串运算符：字符串格式化：三、Tuple（元组）常用运算符四、List（列表）嵌套列表：常用列表操作：五、Dictionary（字典）六、Set（集合）...

编程日记 2023/12/16 5:01:57

hive中如何求取中位数？

目录 中位数的概念代码实现准备数据实现 中位数的概念 中位数（Median）又称中值，统计学中的专有名词，是按顺序排列的一组数据中居于中间位置的数，代表一个样本、种群或概率分布中的一个数值，其可将数值集合…...

编程日记 2023/12/16 5:00:55

在C#中异步编程

在C#中，异步编程是一种编写并发和响应式代码的技术，通过将耗时的操作放在后台线程中执行，以避免阻塞主线程，提高程序的性能和响应性。异步编程使用async和await关键字，结合任务（Task）和异步操作…...

编程日记 2023/12/16 4:59:54

微服务保护--Feign整合Sentinel

限流是一种预防措施，虽然限流可以尽量避免因高并发而引起的服务故障，但服务还会因为其它原因而故障。而要将这些故障控制在一定范围，避免雪崩，就要靠线程隔离（舱壁模式）和熔断降级手段了。 线程隔离之前讲到…...

编程日记 2023/12/16 4:58:54

二进制to十六进制

输入小于等于十六位的二进制数据&#xff0c;输出十六进制数据&#xff1b; #include <stdio.h> #include <stdlib.h> #include <math.h>int main(void) {char arr[16] { 0 }; int array[16] { 0 }; int hex[4] { 0 };int i 0; int num 0;scanf("…...

编程日记 2023/12/16 4:57:53

Logistic 回归算法

Logistic 回归 Logistic 回归算法Logistic 回归简述Sigmoid 函数Logistic 回归模型表达式求解参数 $\theta $梯度上升优化算法 Logistic 回归简单实现使用 sklearn 构建 Logistic 回归分类器Logistic 回归算法的优缺点 Logistic 回归算法 Logistic 回归简述 Logistic 回归是一…...

编程日记 2023/12/16 4:56:52

ubuntu安装详细步骤

一&#xff0c;先下载vmware 1&#xff0c;第一步打开上面链接 下载网址 : https://www.vmware.com/products/workstation-pro/wo rkstation-pro-evaluation.html 许可证 JU090-6039P-08409-8J0QH-2YR7F ZF3R0-FHED2-M80TY-8QYGC-NPKYF FC7D0-D1YDL-M8DXZ-CYPZE-P2AY6 ZC3T…...

编程日记 2023/12/16 4:54:50

力扣5. 最长回文子串

动态规划 思路&#xff1a; 假设 dp[i][j] 为字符串 (i, j) 子串是否为回文的结果&#xff1b;那么 dp[i][j] dp[i 1][j - 1] 且 (s[i] s[j])&#xff1b;长度为1的字符串都是回文&#xff1b; 原字符串长度为1&#xff0c;是回文&#xff1b;原字符串子串长度为1&#xff…...

编程日记 2023/12/16 4:53:49

肆[4]，函数VectorToHomMat2d/AffineTransPoint2d

函数VectorToHomMat2d C形式 LIntExport void VectorToHomMat2d( const HTuple& Px, const HTuple& Py, const HTuple& Qx, const HTuple& Qy, HTuple* HomMat2D);//参数1:图像坐标X数组 //参数2:图像坐标Y数组 //参数3:世界坐标X数组 //参数4:世界坐标Y…...

编程日记 2023/12/16 4:52:48

下载文件 后端返回给前端 response header 响应头

当浏览器在请求资源时&#xff0c;会通过http返回头中的content-type决定如何显示/处理将要加载的数据&#xff0c;如果这个类型浏览器能够支持阅览&#xff0c;浏览器就会直接展示该资源&#xff0c;比如png、jpeg、video等格式。在某些下载文件的场景中&#xff0c;服务端可能…...

编程日记 2023/12/16 4:51:47

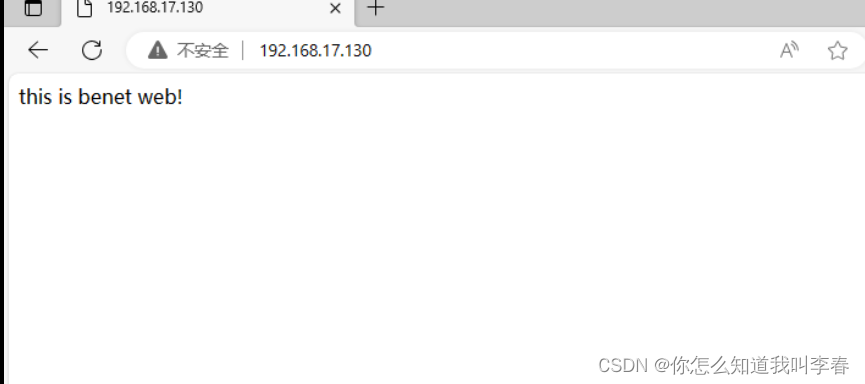
lvs负载均集群

目录 NAT模式 LVS负载均衡群集部署 1.部署共享存储 2.配置节点服务器 192.168.17.130 ​编辑 192.168.17.133 3.配置负载调度器 4.测试效果 NAT模式 LVS负载均衡群集部署 负载调度器&#xff1a;内网关 ens33&#xff1a;192.168.17.70&#xff0c;外网关 ens36&#x…...

编程日记 2023/12/16 4:50:46

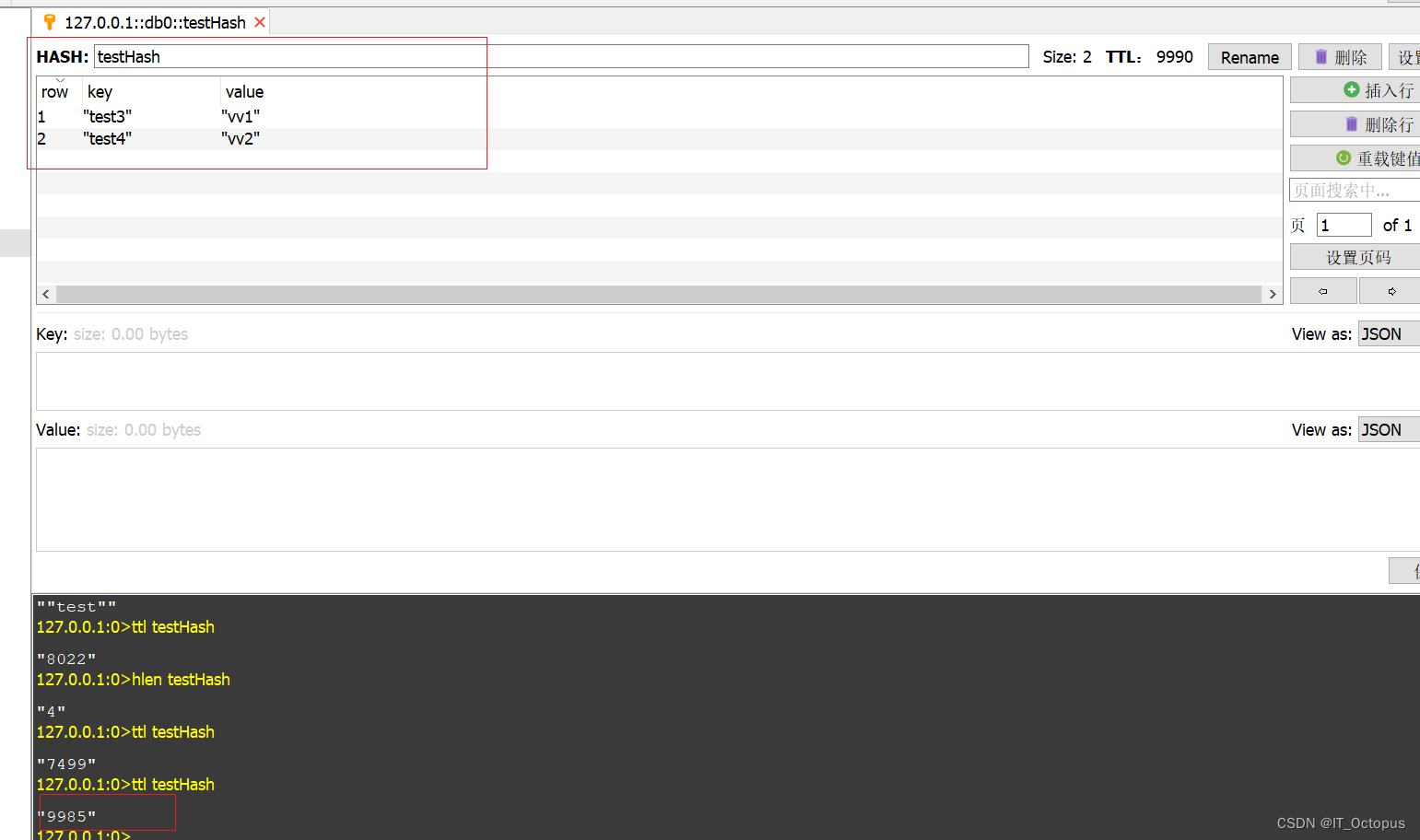
luttuce(RedisTempate)实现hash expire lua脚本

话不多说先放脚本&#xff1a; local argv ARGV local length #argv if length > 0 then local unpackArgs {} for i 1, length - 1 dotable.insert(unpackArgs, argv[i]) end if redis.call(exists, KEYS[1]) 1 thenredis.call(del, KEYS[1])redis.call(hset, KEYS[…...

编程日记 2023/12/16 4:49:45

【Xamarin】WebView连接局域网自动跳转外部浏览器问题的解决

xamarin在中国用的很少&#xff0c;但也有一些独到之处。例如用惯了Visual Studio的就很合适。而且类Java开发&#xff0c;几乎没什么障碍。 protected override void OnCreate(Bundle savedInstanceState) {base.OnCreate(savedInstanceState);Xamarin.Essentials.Platform.I…...

编程日记 2023/12/16 4:48:44

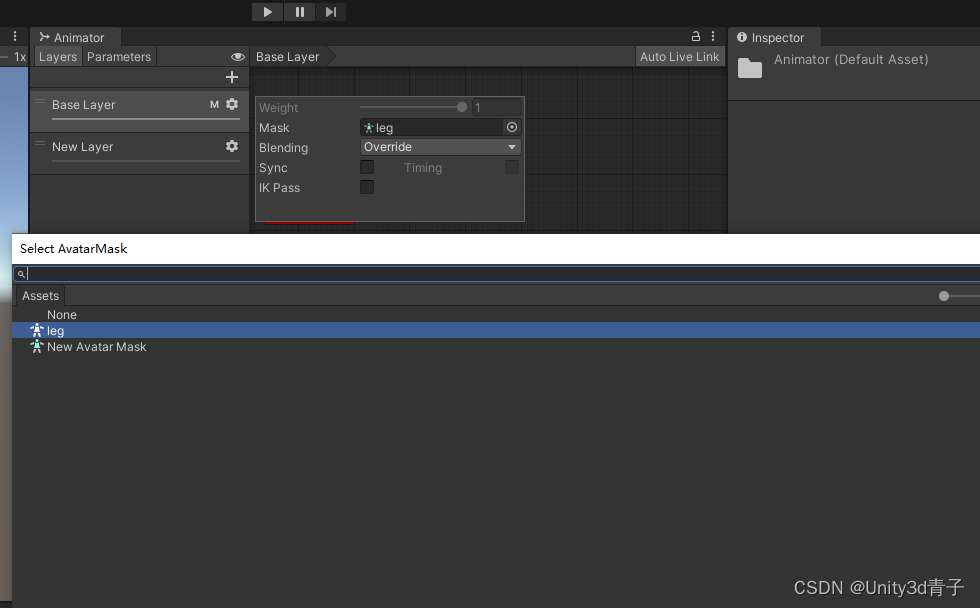
【Unity动画】实现不同的肢体动作自由搭配播放Layer+Avatar Mask

这个教程教你学会使用Unity 动画层配合布偶遮罩&#xff08;AvaterMask&#xff09; 实现从2个动画身上只保留部分肢体动作&#xff0c;然后搭配播放 例如&#xff1a;一个正常跑的动画片段&#xff0c;我只保留腿部动作&#xff0c;形成一个层叫Run_leg 然后在从一个攻击动作…...

编程日记 2023/12/16 4:43:39

将0x06（16进制）转换为二进制

将0x06&#xff08;16进制&#xff09;转换为二进制&#xff0c;可以按照如下步骤进行&#xff1a; 1. 将0x06中的字母"0x"去除。 2. 将数字"06"中的数字"0"去除。 3. 将数字"06"转换为二进制。 根据步骤1和步骤2&#xff0c;去除&q…...

编程日记 2023/12/16 4:41:38

考PRINCE2有用么？有PMP证书了还需要考PRINCE2吗？

有用的&#xff0c;PMP相当于是理论&#xff0c;PRINCE2是实践&#xff0c;对小白来说pmp考后再考一个prince2是很好的选择&#xff0c;对项目管理的小白来说更好入门。 先来说下 prince 2 和 pmp 的区别 一、prince 2 是什么&#xff1f;跟PMP有什么区别&#xff1f; prince…...

编程日记 2023/12/16 4:38:35

06进程间关系-学习笔记

Orphan Process孤儿进程 父进程先于子进程退出&#xff0c;子进程失去托管&#xff0c;这种子进程统称为孤儿进程 失效进程&#xff08;孤儿进程&#xff09;&#xff1a;导致内存泄漏&#xff0c;影响新进程的创建孤儿进程的危害不可预测&#xff0c;如果一个孤儿进程持续的申…...

编程日记 2023/12/16 4:34:32

KubeSphere 容器平台高可用：环境搭建与可视化操作指南

Linux_k8s篇 欢迎来到Linux的世界&#xff0c;看笔记好好学多敲多打&#xff0c;每个人都是大神&#xff01; 题目&#xff1a;KubeSphere 容器平台高可用&#xff1a;环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

编程新知 2026/2/9 18:19:34

突破不可导策略的训练难题：零阶优化与强化学习的深度嵌合

强化学习&#xff08;Reinforcement Learning, RL&#xff09;是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程&#xff0c;然后使用强化学习的Actor-Critic机制&#xff08;中文译作“知行互动”机制&#xff09;&#xff0c;逐步迭代求解…...

编程新知 2026/2/5 4:17:42

数据链路层的主要功能是什么

数据链路层&#xff08;OSI模型第2层&#xff09;的核心功能是在相邻网络节点&#xff08;如交换机、主机&#xff09;间提供可靠的数据帧传输服务&#xff0c;主要职责包括&#xff1a; &#x1f511; 核心功能详解&#xff1a; 帧封装与解封装 封装&#xff1a; 将网络层下发…...

编程新知 2026/2/1 7:31:51

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现，论文初版实现

摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序&#xff0c;以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务&#xff0c;提供稳定高效的数据处理与业务逻辑支持&#xff1b;利用 uniapp 实现跨平台前…...

编程新知 2026/1/31 10:55:22

图表类系列各种样式PPT模版分享

图标图表系列PPT模版&#xff0c;柱状图PPT模版&#xff0c;线状图PPT模版&#xff0c;折线图PPT模版&#xff0c;饼状图PPT模版&#xff0c;雷达图PPT模版&#xff0c;树状图PPT模版 图表类系列各种样式PPT模版分享&#xff1a;图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

编程新知 2026/2/4 18:07:02

Java + Spring Boot + Mybatis 实现批量插入

在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法&#xff1a;使用 MyBatis 的 <foreach> 标签和批处理模式&#xff08;ExecutorType.BATCH&#xff09;。 方法一&#xff1a;使用 XML 的 <foreach> 标签&#xff…...

编程新知 2025/6/11 2:44:05

华为OD机考-机房布局

import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

编程新知 2026/1/31 6:01:08

Python+ZeroMQ实战：智能车辆状态监控与模拟模式自动切换

目录 关键点 技术实现1 技术实现2 摘要&#xff1a; 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式&#xff08;自动驾驶、人工驾驶、远程驾驶、主动安全&#xff09;&#xff0c;并通过实时消息推送更新车…...

编程新知 2025/11/12 0:06:50

从 GreenPlum 到镜舟数据库：杭银消费金融湖仓一体转型实践

作者&#xff1a;吴岐诗&#xff0c;杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言&#xff1a;融合数据湖与数仓的创新之路 在数字金融时代&#xff0c;数据已成为金融机构的核心竞争力。杭银消费金…...

编程新知 2026/1/31 12:30:32

嵌入式常见 CPU 架构

架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集&#xff0c;单周期执行&#xff1b;低功耗、CIP 独立外设&#xff1b;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel&#xff08;原始…...

编程新知 2025/6/10 21:24:01