母婴服务品牌网站的效果如何
随着三胎政策落实及人们生活水平提升，母婴市场发展迅速上升，加之以90后、00后适龄生育的人群悦己消费加强，孕前孕后及婴儿本身就会使用相当好的服务，这也为市场带来了较大机会。
近几年，老品牌在不断加力，而新品牌也在争相入局，母婴行业可以与多个其它行业对接，因此其规模非常庞大。
同时对相关母婴大小企业来说，也面临着一些痛点：
首先就是同行众多，虽然母婴服务包含产品、服务等内容，一般是通过当地进行的，但由于品牌形象低，无法让很多人知悉，线下传播毕竟较为低效，线上朋友圈/发广告等方式也难以起到效果。
很多用户寻找服务或了解品牌都会通过线上方式，不少母婴品牌并没有线上平台，便错失了这部分流量，而且目标客户找不到线上信息，也很难信任及查看品牌信息/服务内容等，无论咨询还是预约等都难以完善。
网站是企业线上门户，可以说是企业经营必备，其主要作用是展示品牌所有内容及用户随时查看互动。官网同样是企业的脸面，自然除了展示内容外，还需要考虑样式、颜色、布局等，其实市场中建站平台很多，但靠谱的却并不会很多。
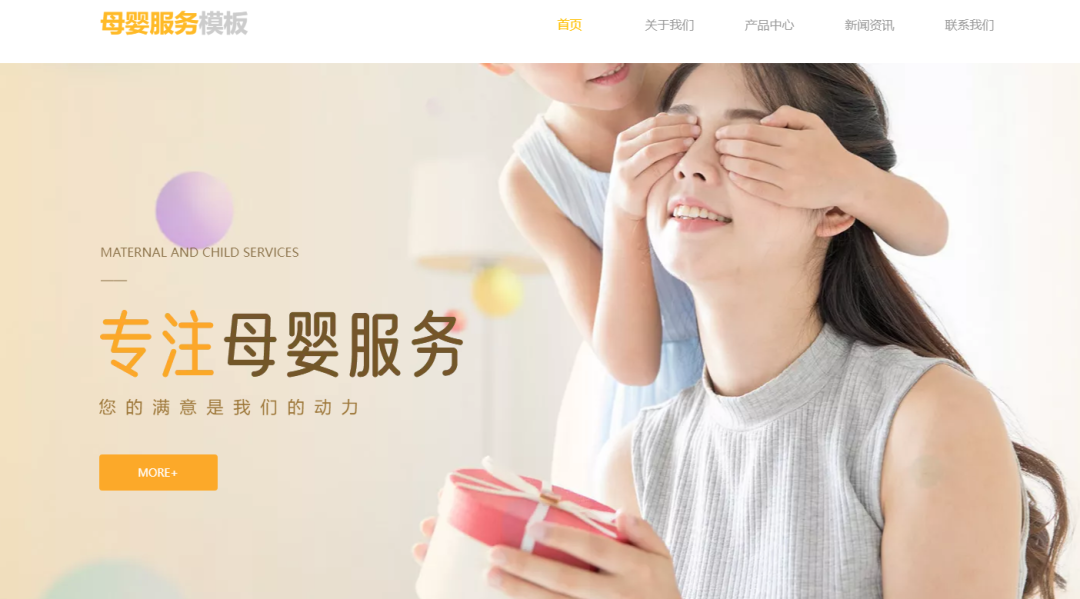
通过【雨科】平台搭建母婴服务网站，现成海量的官网模板样式替换修改即可使用，无论搭建设计还是后台管理都非常简单，无技术要求、一个人也能快速完成建站。
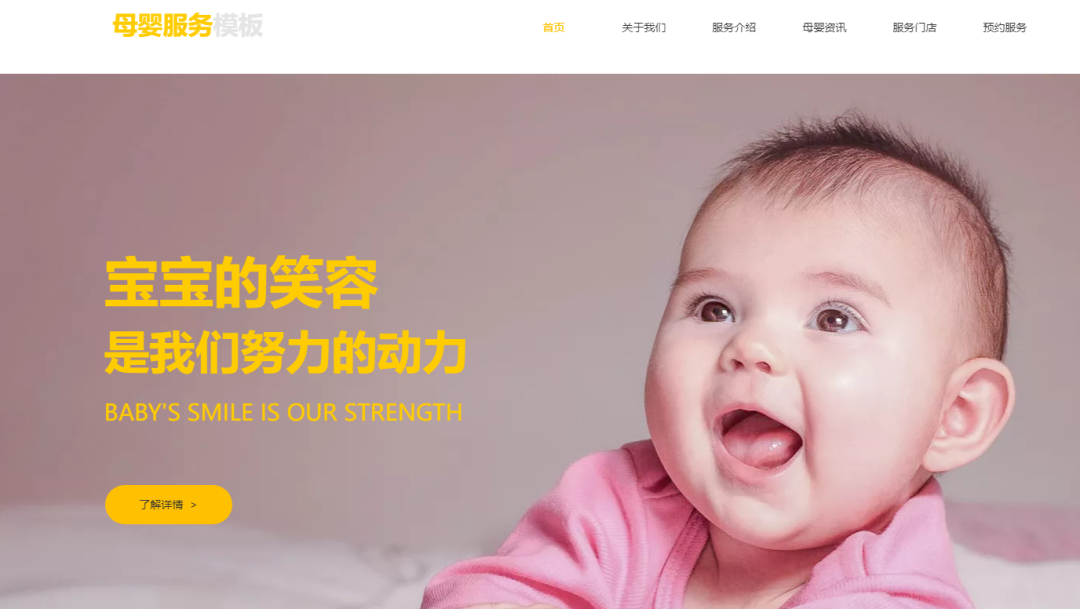
母婴手机微站包括预约、表单、支付、留言、咨询等常用功能控件一应俱全，拖拽式设计搭建，精美布局样式及页面搭建，使得企业可以快速投入使用。建设母婴品牌官网电脑手机端多平台推广获客及赋能用户多平台触达。
现在就搜索【雨科】平台搭建母婴品牌官网吧。
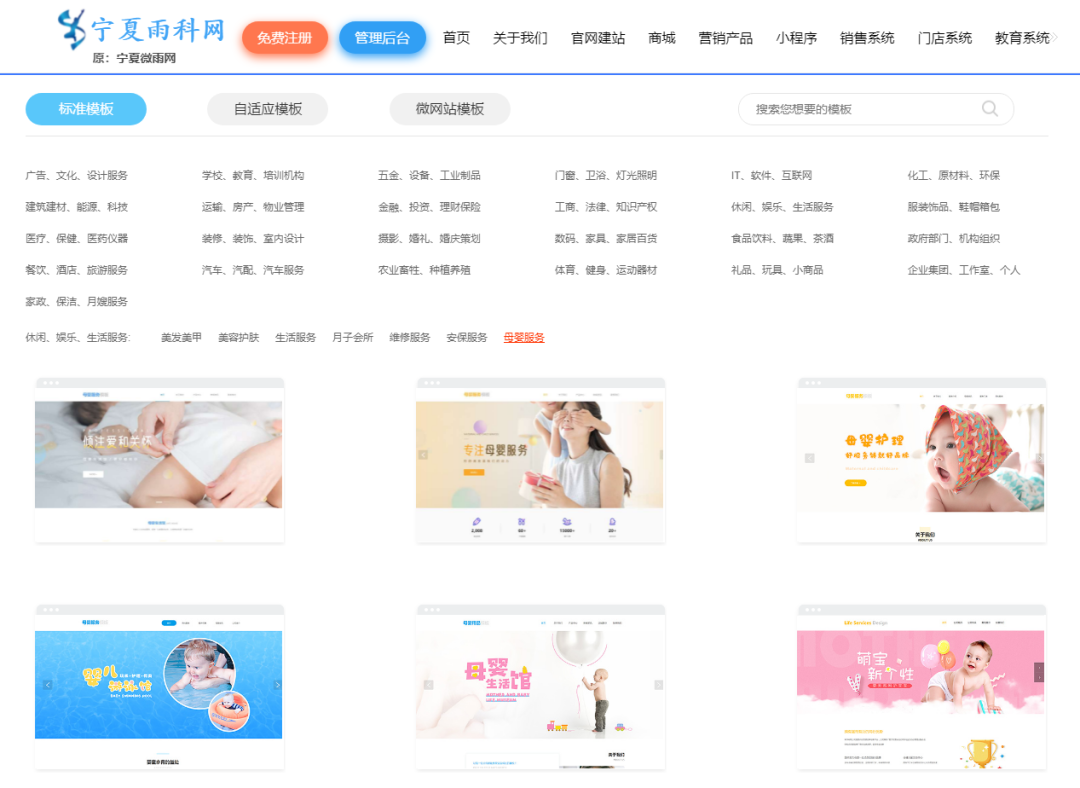
↓↓↓点击“官网”直达
相关文章：
母婴服务品牌网站的效果如何
随着三胎政策落实及人们生活水平提升，母婴市场发展迅速上升，加之以90后、00后适龄生育的人群悦己消费加强，孕前孕后及婴儿本身就会使用相当好的服务，这也为市场带来了较大机会。 近几年，老品牌在不断加力，…...
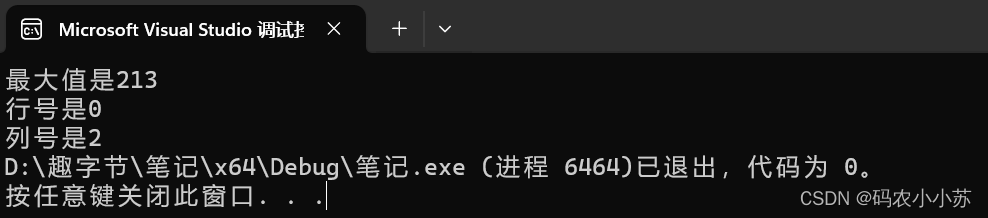
C语言--有一个3*4的矩阵，求出其中最大值的那个元素的值，以及其所在的行号和列号
一.题目描述 有一个3*4的矩阵，要求求出其中最大值的那个元素的值，以及其所在的行号和列号 比如：给定一个3*4的矩阵如下 输出结果：最大值为 12 ，行号为3， 列号为2 二.思路分析 打擂台算法： 先思考…...
安全算法（二）：共享密钥加密、公开密钥加密、混合加密和迪菲-赫尔曼密钥交换
安全算法（二）：共享密钥加密、公开密钥加密、混合加密和迪菲-赫尔曼密钥交换 本章介绍了共享密钥加密、公开密钥加密，和两种加密方法混合使用的混合加密方法；最后介绍了迪菲-赫尔曼密钥交换。 加密数据的方法可以分为…...
MYSQL练题笔记-高级字符串函数 / 正则表达式 / 子句-简单3题
这个系列先写了三题，比较简单写在一起。 1.修复表中的名字相关的表和题目如下 看题目就知道是有关字符串函数的，于是在书里查询相关的函数，如下图，但是没有完全对口的函数，所以我还是去百度了。 然后发现结合上面的4个…...
vue扭蛋机抽奖游戏
简易扭蛋机demo 这是一个使用CSS3和JavaScript实现的扭蛋机抽奖游戏。该游戏的主要功能是通过点击按钮进行抽奖，抽奖过程中会显示滚动的小球，最终随机停止并显示一个中奖小球。 该游戏的抽奖过程如下： 当用户点击抽奖按钮时，首先检查当前是否正在进行抽奖任务或者当前有小…...
代码随想录27期|Python|Day16|二叉树|104.二叉树的最大深度|111.二叉树的最小深度|222.完全二叉树的节点个数
二叉树专题，重点掌握后续的递归和中间节点的处理。 104. 二叉树的最大深度 - 力扣（LeetCode） 本题在前一章已经解决了层序遍历的解法，现在来聊一下递归法。 首先需要明确两个概念：深度和高度。（注意&…...
༺༽༾ཊ—设计-简介-模式—ཏ༿༼༻
我对设计模式的理解就是一种可复用的且面向对象的设计工具，它与代码无关，我们可以利用设计模式设计出高内聚、低耦合的应用程序，并且最大程度实现程序的复用，以应对复杂的需求变化。 程序的可复用性就是用已存在的程序模块进行更新…...
Matplotlib快速入门，Python通用的绘图工具库上手
Matplotlib是一个用于Python编程语言的综合性绘图库。 它可以生成各种类型的图表，包括折线图、条形图、散点图、直方图、饼图等。Matplotlib支持多种数据格式，包括NumPy数组、Pandas DataFrame和CSV文件。它还可以从URL读取数据。 Matplotlib可以在交互…...
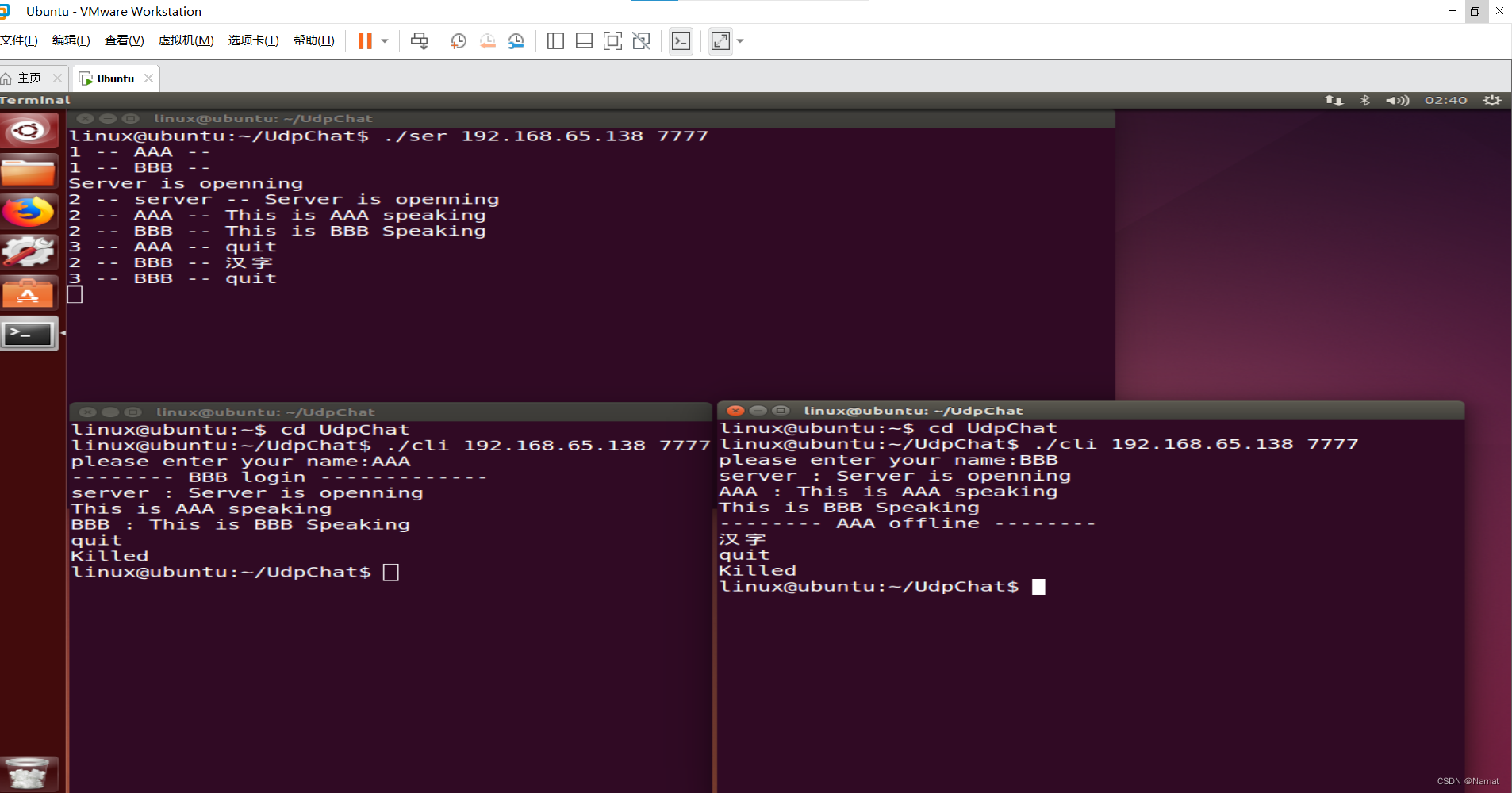
Linux 基本语句_16_Udp网络聊天室
代码： 服务端代码： #include <stdio.h> #include <arpa/inet.h> #include <sys/types.h> #include <sys/socket.h> #include <netinet/in.h> #include <stdlib.h> #include <unistd.h> #include <string…...
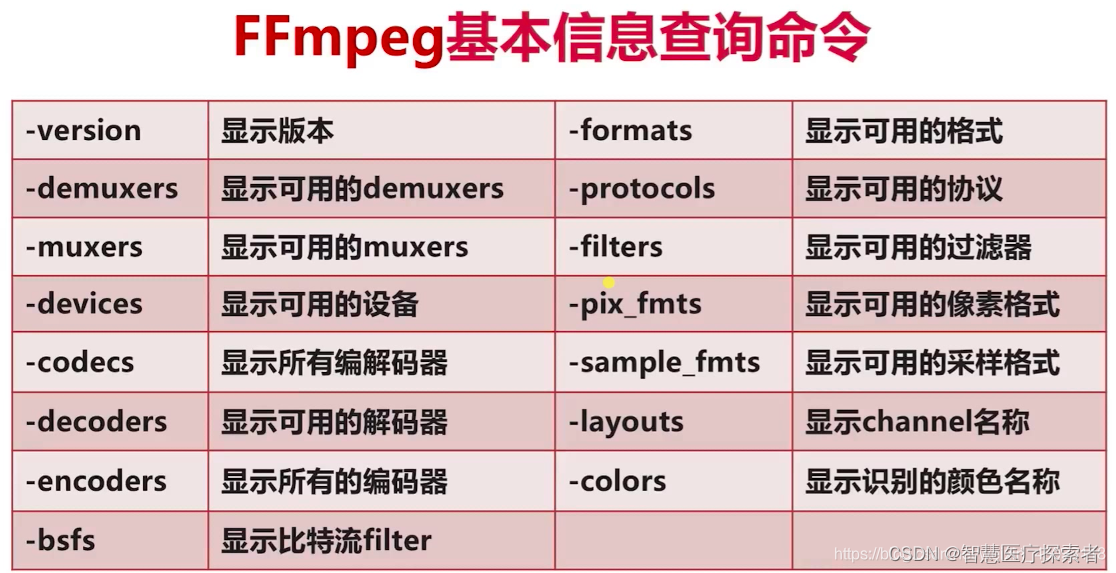
使用ffmpeg命令进行视频格式转换
1 ffmpeg介绍 FFmpeg 是一个非常强大和灵活的开源工具集，用于处理音频和视频文件。它提供了一系列的工具和库，可以用于录制、转换、流式传输和播放音频和视频。 FFmpeg 主要特点如下： 格式支持广泛：FFmpeg 支持几乎所有的音频和视…...
Mac安装Adobe AE/pr/LR/ai/ps/au/dw/id 2024/2023报错问题解决（常见错误：已损坏/2700/146/130/127）
1.打开允许“允许任何来源” 如何打开允许任何来源？在 Finder 菜单栏选择 【前往】 – 【实用工具 】，找到【终端】程序，双击打开，在终端窗口中输入：sudo spctl --master-disable 输入代码后，按【return …...
Python三级 每周练习题31
如果你感觉有收获，欢迎给我微信扫打赏码 ———— 以激励我输出更多优质内容 练习一: 作业1:编写程序，在下面的字典中找出身高137的同学并输出姓名，如果没找到， 输出没有 a{‘小赵’:136,‘小钱’:141,‘小孙’:146,‘小李’:13…...
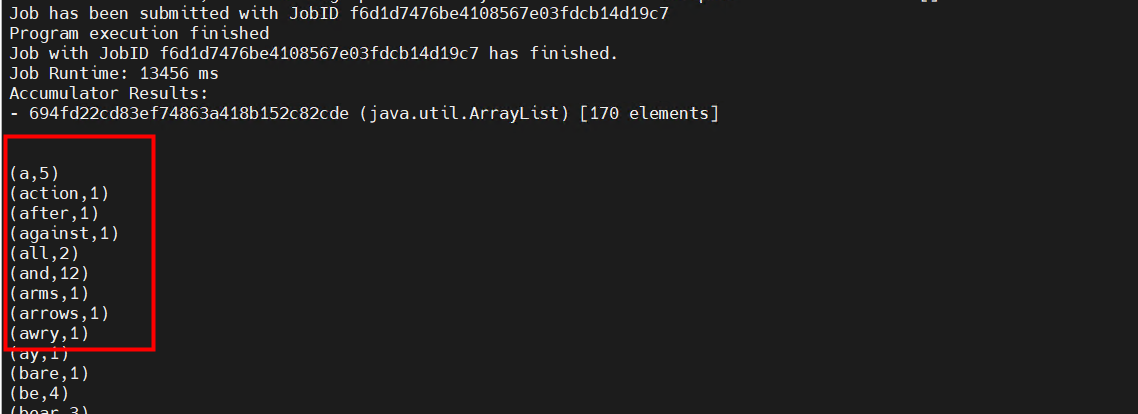
【DataSophon】大数据服务组件之Flink升级
🦄 个人主页——🎐开着拖拉机回家_Linux,大数据运维-CSDN博客 🎐✨🍁 🪁🍁🪁🍁🪁🍁🪁🍁 🪁🍁🪁&am…...
Android笔记（十八）：面向Compose组件结合Retrofit2和Rxjava3实现网络访问
一、Retrofit2 Square公司推出的Retrofit2库（https://square.github.io/retrofit/），改变了网络访问的方式。它实现了网络请求的封装。Retrofit库采用回调处理方式，使得通过接口提交请求和相应的参数的配置，就可以获得…...
mybatis中oracle的sql没走索引导致特别慢（未加jdbcType的）
如果直接跑sql是能走索引很快，在mybatis中不能，可能就是jdbcType的原因。 比如，我有一个属性A，在表里面是VARCHAR2类型，但是在mybatis中的sql是#{a}，缺少jdbcTypeJdbcType.VARCHAR，就会导致myba…...
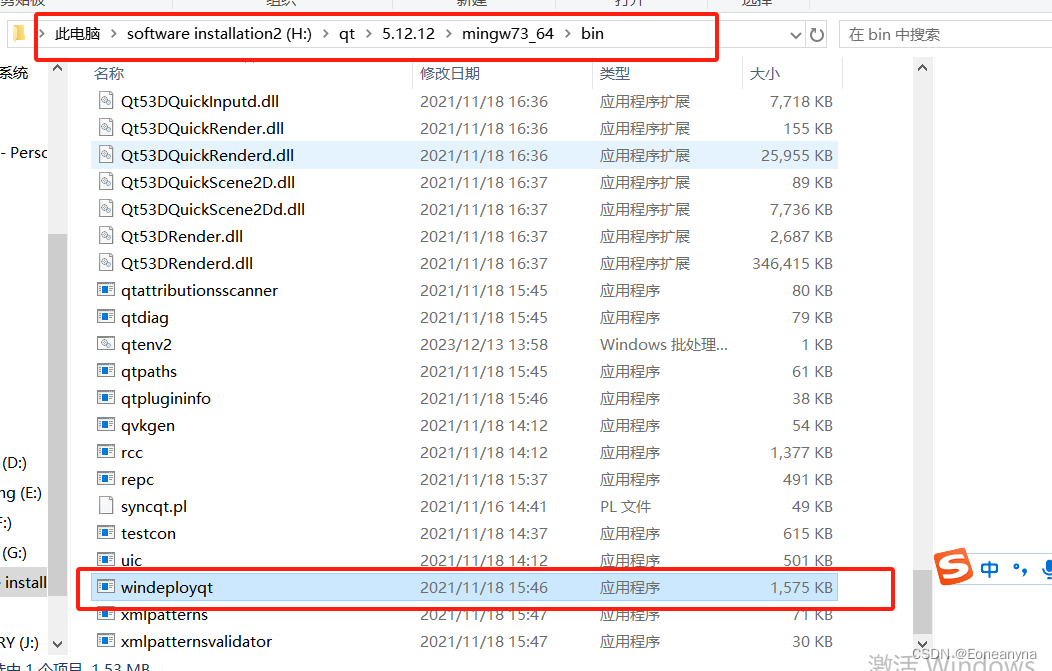
QT自带打包问题：无法定位程序输入点?metaobject@qsound
文章目录 无法定位程序输入点?metaobjectqsound……检查系统环境变量的配置：打包无须安装qt的文件 无法定位程序输入点?metaobjectqsound…… 在执行release打包程序后，相应的release文件夹下的exe文件，无法打开 如有错误欢迎指出 检查系…...
7.3 lambda函数
一、语法 1.基础语法 [capture](paramLists) mutable ->retunType{statement} capture。捕获列表，用于捕获前文的变量供lambda函数中使用，可省略。(paramLists)。参数列表，可省略。mutable。lambda表达式默认具有常量性，可以…...
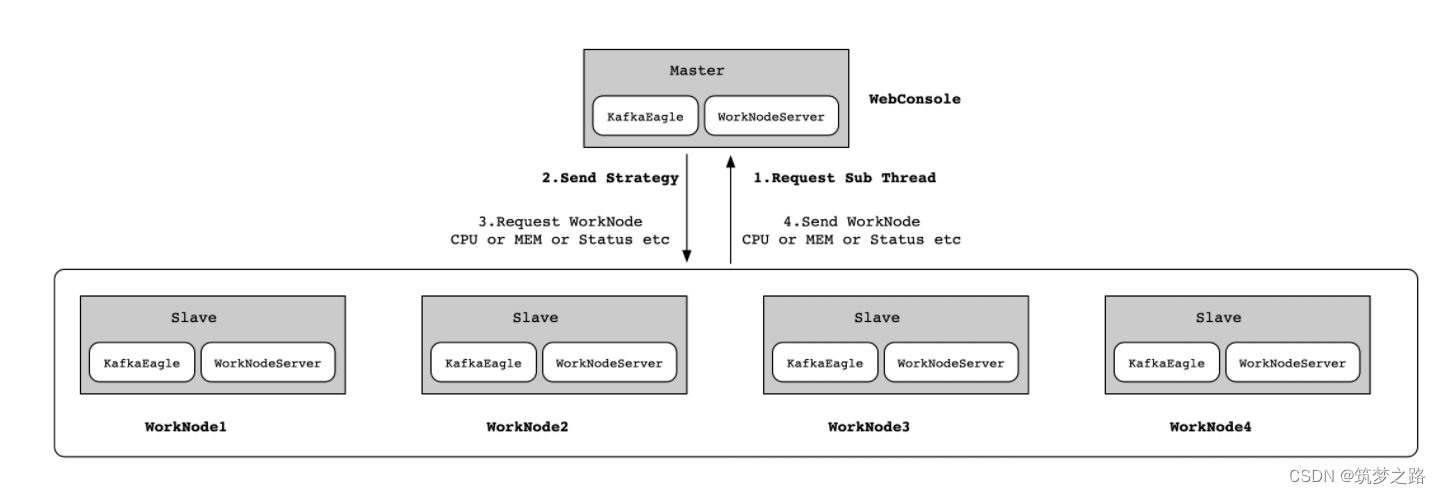
dcoker-compose一键部署EFAK —— 筑梦之路
简介 EFAK（Eagle For Apache Kafka，以前称为 Kafka Eagle）是一款由国内公司开源的Kafka集群监控系统，可以用来监视kafka集群的broker状态、Topic信息、IO、内存、consumer线程、偏移量等信息，并进行可视化图表展示。独…...
音视频：Ubuntu下安装 FFmpeg 5.0.X
1.安装相关依赖 首可选一： sudo apt-get update sudo apt-get install build-essential autoconf automake libtool pkg-config \libavcodec-dev libavformat-dev libavutil-dev \libswscale-dev libresample-dev libavdevice-dev \libopus-dev libvpx-dev libx2…...
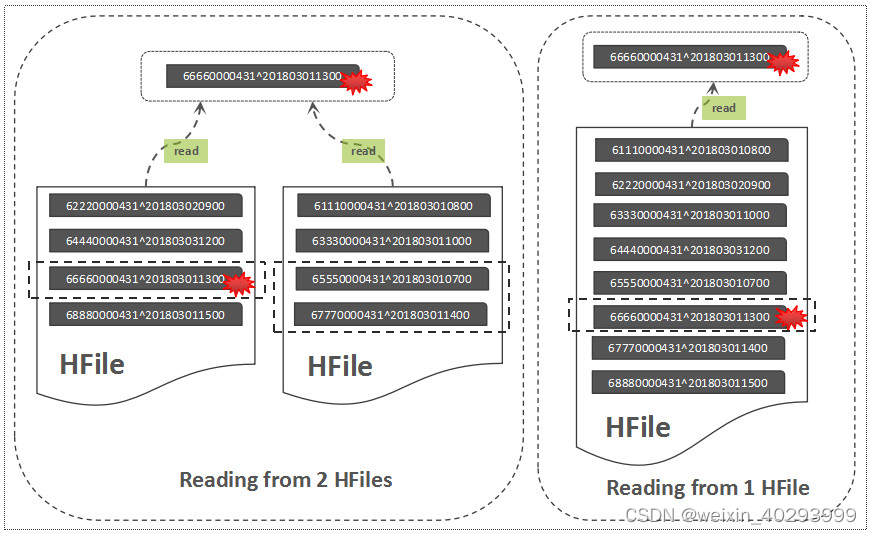
【LSM tree 】Log-structured merge-tree 一种分层、有序、面向磁盘的数据结构
文章目录 前言基本原理读写流程写流程读流程 写放大、读放大和空间放大优化 前言 LSM Tree 全称是Log-structured merge-tree, 是一种分层，有序，面向磁盘的数据结构。其核心原理是磁盘批量顺序写比随机写性能高很多，可以通过围绕这一原理进行…...
日语AI面试高效通关秘籍：专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下，越来越多的求职者将目光投向了日本及中日双语岗位。但是，一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧？面对生疏的日语交流环境，即便提前恶补了…...
基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容：参考网站： PID算法控制 PID即：Proportional（比例）、Integral（积分&…...
【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引，可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度（创建索引的主要原因）。3. 可以加速表和表之间的连接，实现数据的参考完整性。4. 可以在查询过程中，…...
【Java学习笔记】Arrays类
Arrays 类 1. 导入包：import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序（自然排序和定制排序）Arrays.binarySearch()通过二分搜索法进行查找（前提：数组是…...
线程同步：确保多线程程序的安全与高效！
全文目录： 开篇语前序前言第一部分：线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分：synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...
【SQL学习笔记1】增删改查+多表连接全解析（内附SQL免费在线练习工具）
可以使用Sqliteviz这个网站免费编写sql语句，它能够让用户直接在浏览器内练习SQL的语法，不需要安装任何软件。 链接如下： sqliteviz 注意： 在转写SQL语法时，关键字之间有一个特定的顺序，这个顺序会影响到…...
OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成，核心是利用 HTTP 协议的 Range 请求头指定下载范围： 实现原理 Range 请求头：向服务器请求文件的特定字节范围（如 Range: bytes1024-） 本地文件记录：保存已…...
unix/linux，sudo，其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化，本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来，让我们拨开时间的迷雾，一同探寻 sudo 那波澜壮阔（也颇为实用主义）的发展历程。 历史背景：su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前，Unix 系统管理员和需要特权操作的…...
三体问题详解
从物理学角度，三体问题之所以不稳定，是因为三个天体在万有引力作用下相互作用，形成一个非线性耦合系统。我们可以从牛顿经典力学出发，列出具体的运动方程，并说明为何这个系统本质上是混沌的，无法得到一般解…...
《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码： https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...