智能优化算法应用:基于阿基米德优化算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于阿基米德优化算法3D无线传感器网络(WSN)覆盖优化 - 附代码
文章目录
- 智能优化算法应用:基于阿基米德优化算法3D无线传感器网络(WSN)覆盖优化 - 附代码
- 1.无线传感网络节点模型
- 2.覆盖数学模型及分析
- 3.阿基米德优化算法
- 4.实验参数设定
- 5.算法结果
- 6.参考文献
- 7.MATLAB代码
摘要:本文主要介绍如何用阿基米德优化算法进行3D无线传感器网(WSN)覆盖优化。
1.无线传感网络节点模型
本文主要基于0/1模型,进行寻优。在二维平面上传感器节点的感知范围是一个以节点为圆心,半径为 R n R_n Rn的圆形区域,该圆形区域通常被称为该节点的“感知圆盘”, R n R_n Rn称为传感器节点的感知半径,感知半径与节点内置传感器件的物理特性有关,假设节点 n n n的位置坐标为 ( x n , y n , z n ) (x_n,y_n,z_n) (xn,yn,zn)在0-1感知模型中,对于平面上任意一点 p ( x p , y p , z p ) p(x_p,y_p,z_p) p(xp,yp,zp),则节点 n n n监测到区域内点 p p p的事件发生概率为:
P r ( n , p ) = { 1 , d ( n , p ) ≤ R n 0 , e s l e (1) P_r(n,p)=\begin{cases}1, \,d(n,p)\leq R_n\\ 0,\, esle \end{cases}\tag{1} Pr(n,p)={1,d(n,p)≤Rn0,esle(1)
其中 d ( n , p ) = ( x n − x p ) 2 + ( y n − y p ) 2 + ( z n − z p ) 2 d(n,p)=\sqrt{(x_n-x_p)^2+(y_n-y_p)^2 + (z_n-z_p)^2} d(n,p)=(xn−xp)2+(yn−yp)2+(zn−zp)2为点和之间的欧式距离。
2.覆盖数学模型及分析
现假定目标监测区域为二维平面,在区域 A r e a Area Area上投放同型结构传感器节点的数目为N,每个节点的位置坐标值假设已被初始化赋值,且节点的感知半径r。传感器节点集则表示为:
N o d e { x 1 , . . . , x N } (2) Node\{x_1,...,x_N\} \tag{2} Node{x1,...,xN}(2)
其中 n o d e i = { x i , y i , z i , r } node_i=\{x_i,y_i,z_i,r\} nodei={xi,yi,zi,r},表示以节点 ( x i , y i , z i ) (x_i,y_i,z_i) (xi,yi,zi)为圆心,r为监测半径的球,假定监测区域 A r e a Area Area被数字化离散为 m ∗ n ∗ l m*n*l m∗n∗l个空间点,空间点的坐标为 ( x , y , z ) (x,y,z) (x,y,z),目标点与传感器节点间的距离为:
d ( n o d e i , p ) = ( x i − x ) 2 + ( y i − y ) 2 + ( z i − z ) 2 (3) d(node_i,p)=\sqrt{(x_i-x)^2+(y_i-y)^2 + (z_i-z)^2}\tag{3} d(nodei,p)=(xi−x)2+(yi−y)2+(zi−z)2(3)
目标区域内点被传感器节点所覆盖的事件定义为 c i c_i ci。则该事件发生的概率 P c i P{c_i} Pci即为点 ( x , y , z ) (x,y,z) (x,y,z)被传感器节点 n o d e i node_i nodei所覆盖的概率:
P c o v ( x , y , z , n o d e i ) = { 1 , i f d ( n o d e i , p ) ≤ r 0 , e s l e (4) P_{cov}(x,y,z,node_i)=\begin{cases}1, if\,d(node_i,p)\leq r\\ 0,\, esle \end{cases}\tag{4} Pcov(x,y,z,nodei)={1,ifd(nodei,p)≤r0,esle(4)
我们将所有的传感器节点在目标监测环境中的区域覆盖率 C o v e r R a t i o CoverRatio CoverRatio定义为传感器节点集的覆盖面积与监测区域的面积之比,如公式所示:
C o v e r R a t i o = ∑ P c o v m ∗ n ∗ l (5) CoverRatio = \frac{\sum P_{cov}}{m*n*l}\tag{5} CoverRatio=m∗n∗l∑Pcov(5)
那我们的最终目标就是找到一组节点使得覆盖率最大。
3.阿基米德优化算法
阿基米德优化算法原理请参考:https://blog.csdn.net/u011835903/article/details/119999874
阿基米德优化算法是寻找最小值。于是适应度函数定义为未覆盖率最小,即覆盖率最大。如下:
f u n = a r g m i n ( 1 − C o v e r R a t i o ) = a r g m i n ( 1 − ∑ P c o v m ∗ n ∗ l ) (6) fun = argmin(1 - CoverRatio) = argmin(1-\frac{\sum P_{cov}}{m*n*l}) \tag{6} fun=argmin(1−CoverRatio)=argmin(1−m∗n∗l∑Pcov)(6)
4.实验参数设定
无线传感器覆盖参数设定如下:
%% 设定WNS覆盖参数,
%% 默认输入参数都是整数,如果想定义小数,请自行乘以系数变为整数再做转换。
%% 比如范围1*1,R=0.03可以转换为100*100,R=3;
%区域范围为AreaX*AreaY*AreaZ
AreaX = 100;
AreaY = 100;
AreaZ = 100;
N = 20 ;%覆盖节点数
R = 15;%通信半径阿基米德优化算法参数如下:
%% 设定阿基米德优化优化参数
pop=30; % 种群数量
Max_iteration=30; %设定最大迭代次数
lb = ones(1,3*N);
ub = [AreaX.*ones(1,N),AreaY.*ones(1,N),AreaZ.*ones(1,N)];
dim = 3*N;%维度为3N,N个坐标点
5.算法结果


从结果来看,覆盖率在优化过程中不断上升。表明阿基米德优化算法对覆盖优化起到了优化的作用。
6.参考文献
[1] 史朝亚. 基于PSO算法无线传感器网络覆盖优化的研究[D]. 南京理工大学.
7.MATLAB代码
相关文章:

智能优化算法应用:基于阿基米德优化算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于阿基米德优化算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于阿基米德优化算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.阿基米德优化算法4.实验参数设定…...
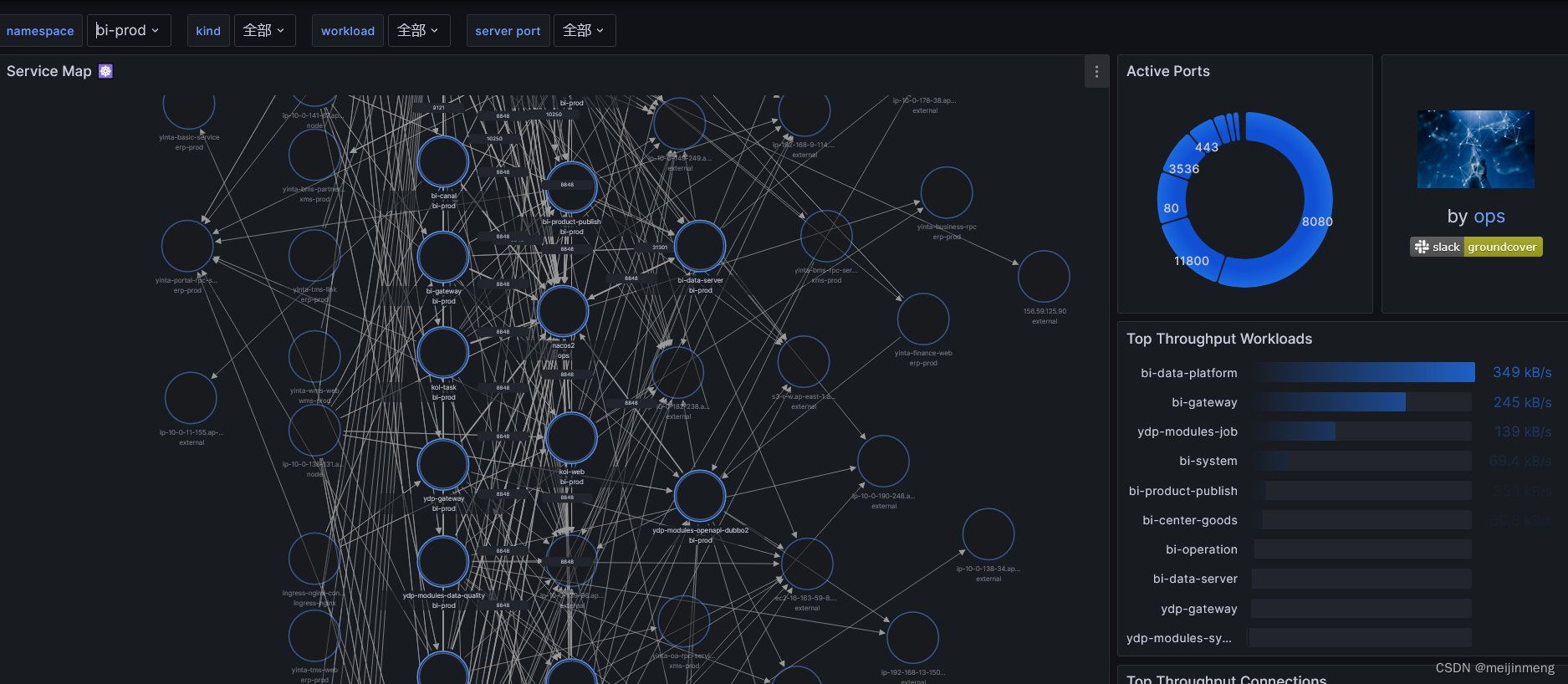
K8s内容器拓扑图工具
1.背景:随着线上容器越来越多,需要一个可视化的方式展示各个容器之间的拓扑图。 2.需求:轻量级,部署方便。 3.部署 helm repo add groundcover https://helm.groundcover.com/ helm repo update helm install caretta --namespa…...
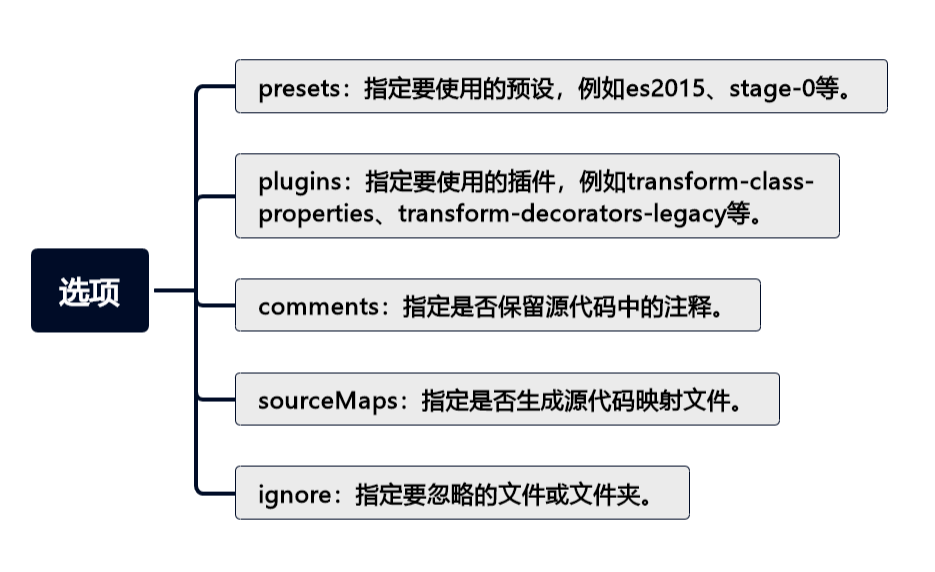
掌握 Babel:让你的 JavaScript 与时俱进(上)
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...
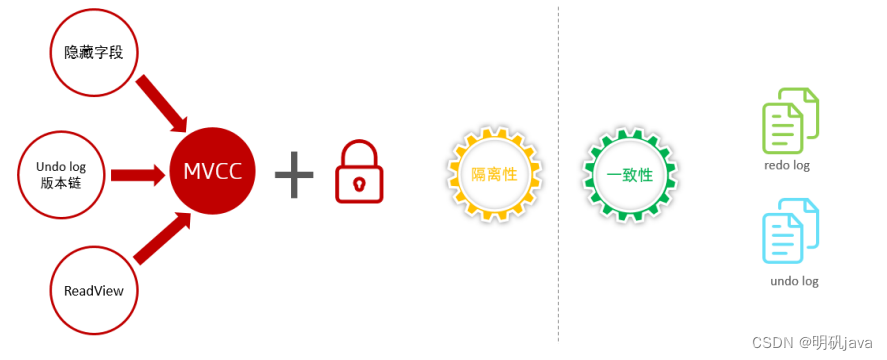
Mysql进阶-InnoDB引擎事务原理及MVCC
事务原理 事务基础 事务是一组操作的集合,它是一个不可分割的工作单位,事务会把所有的操作作为一个整体一起向系 统提交或撤销操作请求,即这些操作要么同时成功,要么同时失败。 事务的四大特性: 原子性(A…...
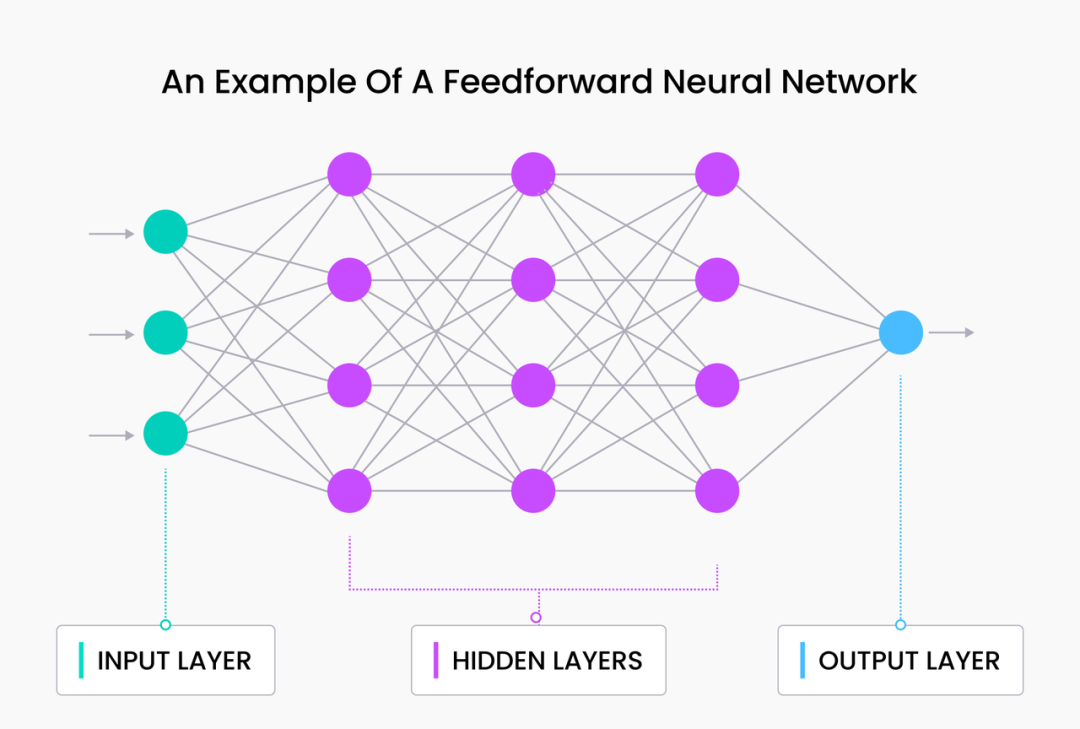
「X」Embedding in NLP|神经网络和语言模型 Embedding 向量入门
在「X」Embedding in NLP 进阶系列中,我们介绍了自然语言处理的基础知识——自然语言中的 Token、N-gram 和词袋语言模型。今天,我们将继续和大家一起“修炼”,深入探讨神经网络语言模型,特别是循环神经网络,并简要了解…...
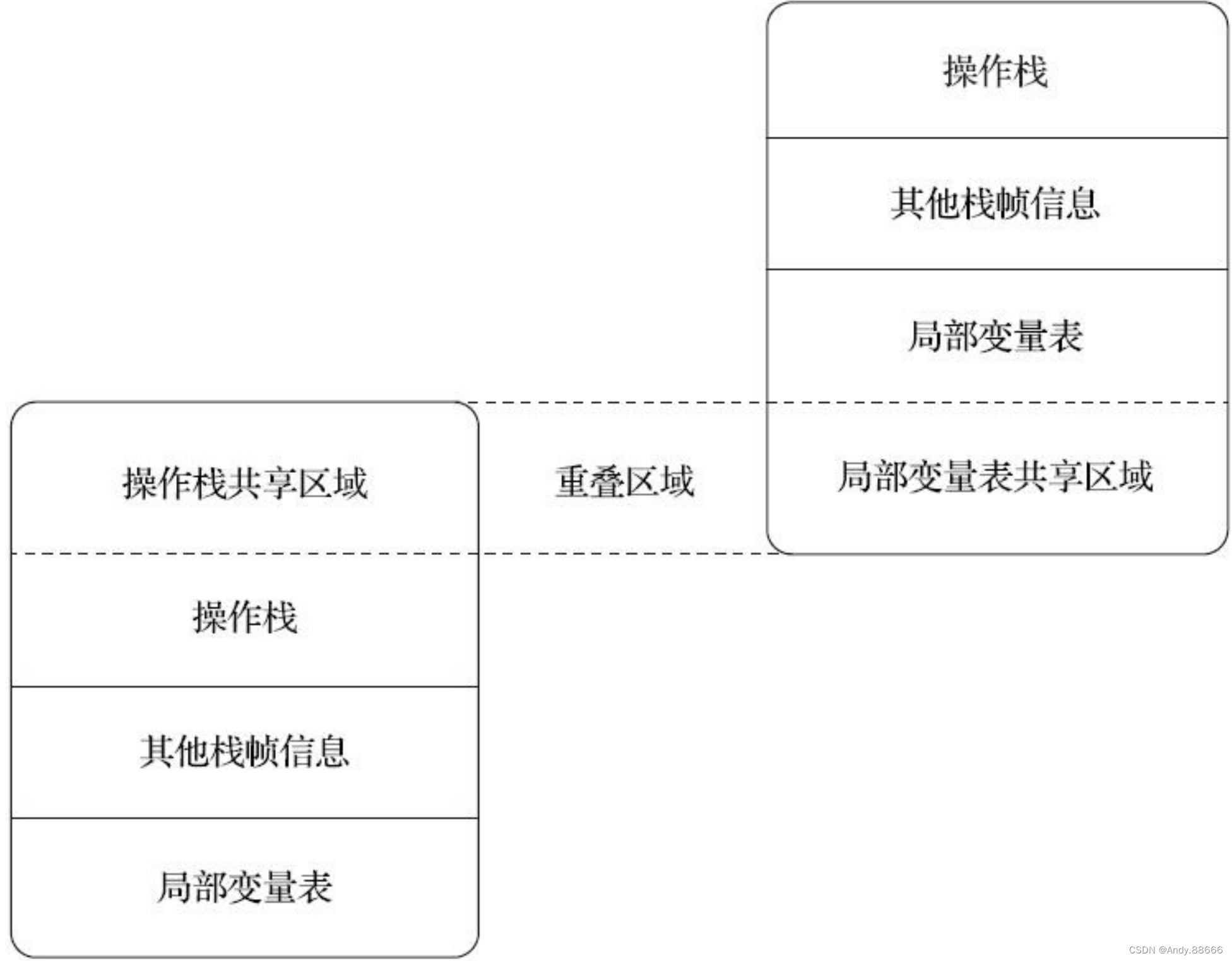
JVM-11-运行时栈帧结构
“栈帧”(Stack Frame)则是用于支持虚拟机进行方法调用和方法执行背后的数据结构,它也是虚拟机运行时数据区中的虚拟机栈(Virtual MachineStack)的栈元素。 栈帧存储了方法的局部变量表、操作数栈、动态连接和方法返回…...

【经典LeetCode算法题目专栏分类】【第6期】二分查找系列:x的平方根、有效完全平方数、搜索二位矩阵、寻找旋转排序数组最小值
《博主简介》 小伙伴们好,我是阿旭。专注于人工智能AI、python、计算机视觉相关分享研究。 ✌更多学习资源,可关注公-仲-hao:【阿旭算法与机器学习】,共同学习交流~ 👍感谢小伙伴们点赞、关注! X的平方根 class Soluti…...
)
【大麦小米学量化】使用xtquant调用迅投MiniQMT客户端定时操作逆回购,再也不担心忘了赚零花钱了(含完整源代码)
文章目录 前言一、逆回购是什么?1. 什么是逆回购?2. 最低参与金额是多少?3. 逆回购交易是否安全?4. 逆回购交易适合什么类型的客户? 二、讯投XtQuant是什么?1. XtQuant运行依赖环境2. XtQuant运行逻辑 三、…...
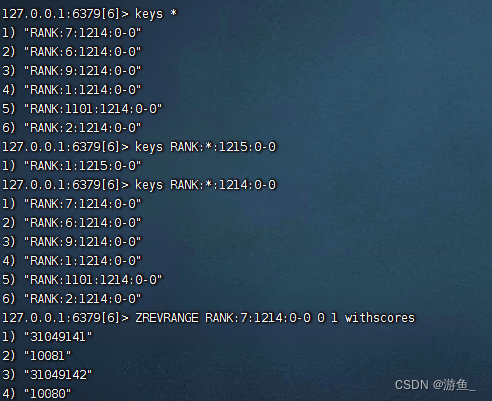
php hyperf 读取redis,存储到数据库
背景说明 小白:伟哥,java中的set是无序的,Redis中可以带顺序吗? 伟哥:可以, 不过不叫set了,叫zset。 概述 SortedSet又叫zset,它是Redis提供的特殊数据类型,是一种特殊…...

云原生之深入解析K8S 1.27新特性如何简化状态服务跨集群平滑迁移
一、背景 Kubernetes v1.26 为 StatefulSet 引入了一个新的 Alpha 级别特性,可以控制 Pod 副本的序号。从 Kubernetes v1.27 开始,此特性进级到 Beta 阶段。序数可以从任意非负数开始, 那么该如何使用此功能呢?StatefulSet 序号为…...
鸿蒙OS:打破界限的操作系统新星
导言 鸿蒙OS(HarmonyOS)是华为公司为应对技术封锁而推出的分布式操作系统,其背后蕴含着华为构建全球数字生活愿景的雄心。本文将深入剖析鸿蒙OS的起源、核心特性,并展望其未来在数字生态中的角色。 1. 背景与起源 华为的…...
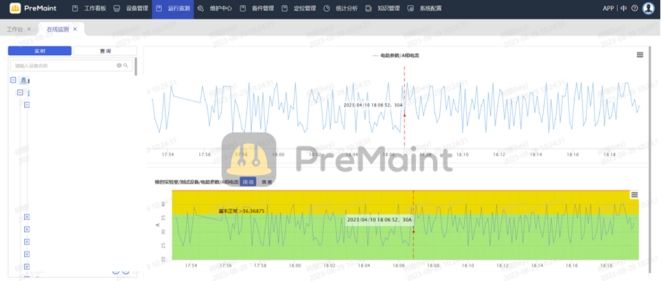
预测性维护在汽车制造行业中的应用
汽车制造行业是一个高度复杂和精细化的领域,依赖于各种设备来完成生产流程。这些设备包括机械装配线、焊接机器人、喷涂设备、传送带等。然而,这些设备在长时间运行中不可避免地会遇到各种故障,给生产进程带来延误和成本增加。为了应对这一挑…...

分布式链路追踪 —— 基于Dubbo的traceId追踪传递
文章目录 原文链接RpcContext 上下文对象Dubbo 过滤器(Filter)对象基于Dubbo的traceId追踪传递实现 原文链接 RpcContext 上下文对象 在实现 Dubbo 调用之间的链路跟踪之前,先简单了解 RpcContext 上下文对象和 Filter 过滤器对象ÿ…...
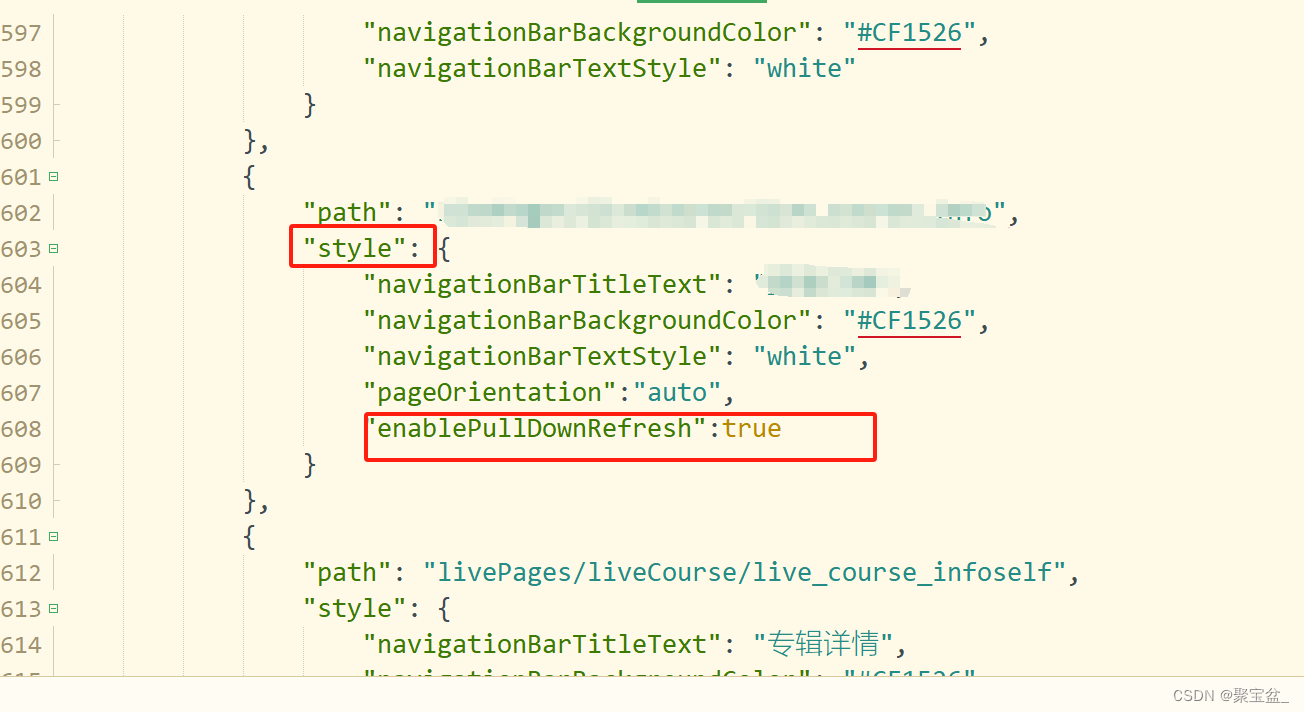
【uniapp小程序-上拉加载】
在需要上拉加载的页面的page.json上添加红框框里面的 onReachBottom() {if(this.commentCurrent<this.commentTotal){this.commentCurrent 1; this.commentList();this.status loading;}else{this.status ;} }, methods:{commentList(){let params {courseid:this.cour…...

ubuntu添加路由
ip route show 查看当前路由表 sudo ip route add /mask via 添加一条路由 目标ip 1.1.1.1/100 下一跳 2.2.2.2 sudo ip route add 1.1.1.1/100 via 2.2.2.2 dev ens160 proto static metric 100这是一条Linux命令,用于添加一个静态路由。具体含义如下࿱…...
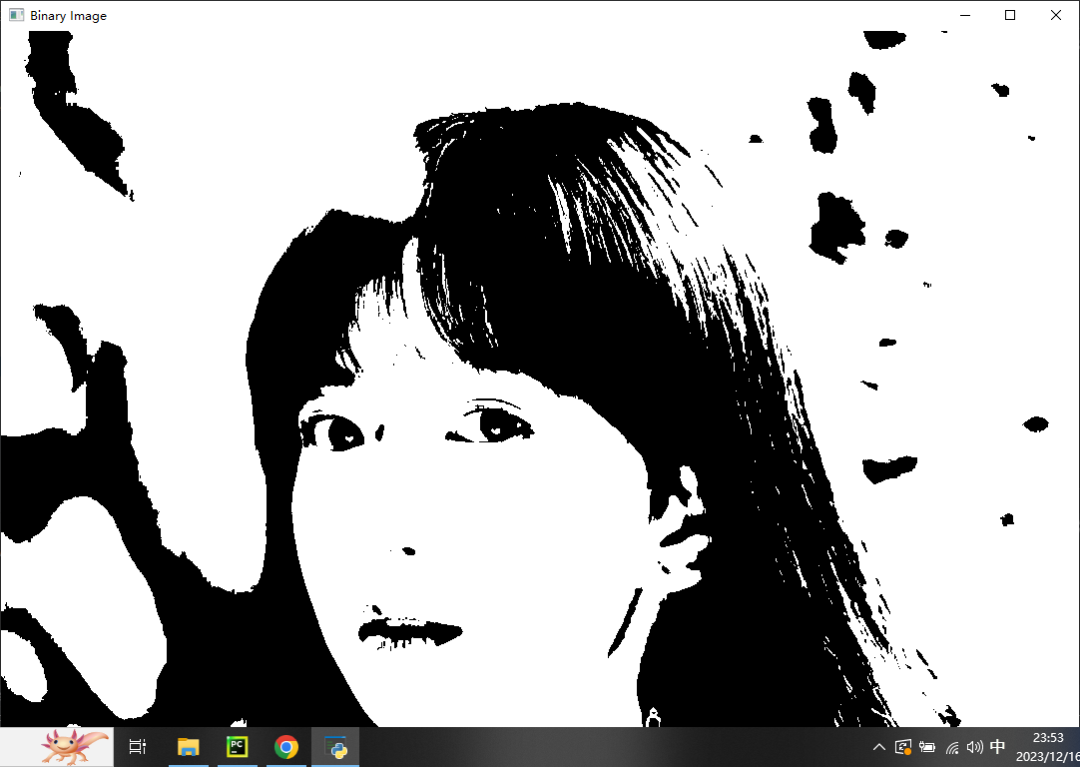
python图像二值化处理
目录 1、双峰法 2、P参数法 3、迭代法 4、OTSU法 图像的二值化处理是将图像上的像素点的灰度值设置为0或255,也就是将整个图像呈现出明显的只有黑和白的视觉效果。二值化是图像分割的一种最简单的方法,可以把灰度图像转换成二值图像。具体实现是将大…...

4.配置系统时钟思路及方法
前言: 比起之前用过的三星的猎户座4412芯片,STM32F4的系统时钟可以说是小巫见大巫,首先我们需要清晰时钟产生的原理:几乎大多数的芯片都是由晶振产生一个比较低频的频率,然后通过若干个PLL得到单片机能承受的频率&…...

使用openMVS库,在VS2022中启用c++17标准编译仍然报错
使用openMVS库,在VS2022中启用c17标准编译仍然报错 现象 项目中引用了某些开源库(例如openmvs2.1.0),编译时要求启用编译器对c17的支持。 没问题!大家都知道在下图所示的位置调整C语言标准: 但是&#…...
uniGUI之上传文件UniFileUploadButton
TUniFileUploadButton主要属性: Filter: 文件类型过滤,有图片image/* audio/* video/*三种过滤 MaxAllowedSize: 设置文件最大上传尺寸; Message:标题以及消息文本,可翻译成中文 TUniFileUploadButton控件 支持多…...

福德植保无人机工厂:创新科技与绿色农业的完美结合
亲爱的读者们,欢迎来到福德植保无人机工厂的世界。这里,科技与农业的完美结合为我们描绘出一幅未来农业的新篇章。福德植保无人机工厂作为行业的领军者,以其领先的无人机技术,创新的理念,为我们展示了一种全新的农业服…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

聚六亚甲基单胍盐酸盐市场深度解析:现状、挑战与机遇
根据 QYResearch 发布的市场报告显示,全球市场规模预计在 2031 年达到 9848 万美元,2025 - 2031 年期间年复合增长率(CAGR)为 3.7%。在竞争格局上,市场集中度较高,2024 年全球前十强厂商占据约 74.0% 的市场…...
