PCL 点云匹配 之NICP(Normal ICP)
一、概述
上面一篇中我们已经得出了一个结论,就是ICP虽然简单,但是也有明显的缺点
1、计算速度慢,收敛慢,迭代次数多
2、对内存的开销比较大
3、很容易陷入局部最优的困局
因此我们在经典ICP的基础上添加一两个约束:
第一个约束就是添加法向量,计算当前点R半斤内的法向量,算法向量的夹角
第二个约束就是添加曲率,添加曲率
这样我们就可以减少迭代的次数,加速收敛。
二、计算点云的法向量和曲率
原理:
找到当前点pi的r 半斤类的所有的点V,然后计算出当前点集V的均值ui,然后开始计算V到的协方差

由于协方差的对称性,我们可以对这个矩阵进行SVD矩阵分解


曲率:
是按照从小到大的顺序排列的,那么曲率可以计算:
,并且
越小表示当前点云半斤内越平坦
最小的特征值对应的就是法向量的方向。
数学技巧篇69:特征值、特征向量的求法与证明 - 知乎
法向量
求解最小特征值的特征向量即为法向量


法向量的定向
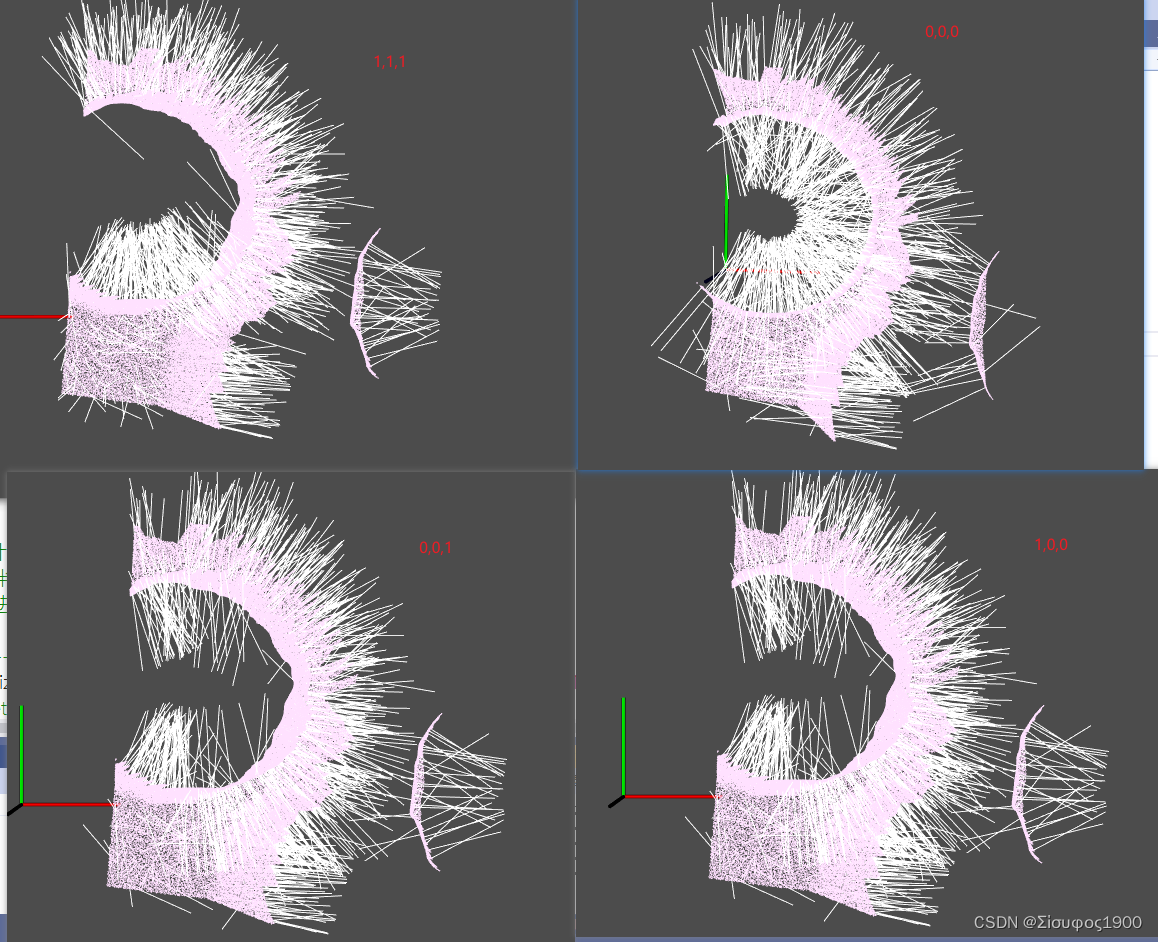
从上面我们可以计算出法向量,那么法向量如何定向呢,也就是说一条直线你规定那个方向为正方向呢???
可以用视点Vp *Ni(当前点的法向量) >0 为正 等
PCL中的法向量定向
已知视点Vp ,对于任意的半径内的点坐标Pi 以及其对应的法向量ni,其定向如下:

flipNormalTowardsViewpoint (const PointT &point, float vp_x, float vp_y, float vp_z, Eigen::Vector4f &normal);
法向量方向测试

比较如下
code
#include <pcl/io/pcd_io.h>
#include <pcl/kdtree/kdtree_flann.h>
//#include <pcl/features/normal_3d.h>
#include <pcl/features/normal_3d_omp.h>
#include <pcl/visualization/pcl_visualizer.h>
#include <boost/thread/thread.hpp>
#include "vtkAutoInit.h"
VTK_MODULE_INIT(vtkRenderingOpenGL);
VTK_MODULE_INIT(vtkInteractionStyle);
VTK_MODULE_INIT(vtkRenderingFreeType)#if 1int main()
{//------------------加载点云数据-------------------//C:\Users\Albert\Desktop\halcon_to_pcl\normal\normaltest2.pcdpcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);if (pcl::io::loadPCDFile<pcl::PointXYZ>("C:\\Users\\Albert\\Desktop\\halcon_to_pcl\\classfiy\\0.pcd", *cloud) == -1){// 找不到点云文件return -1;}//------------------计算法线----------------------pcl::NormalEstimationOMP<pcl::PointXYZ, pcl::Normal> n;//OMP加速pcl::PointCloud<pcl::Normal>::Ptr normals(new pcl::PointCloud<pcl::Normal>);//建立kdtree来进行近邻点集搜索pcl::search::KdTree<pcl::PointXYZ>::Ptr tree(new pcl::search::KdTree<pcl::PointXYZ>());n.setNumberOfThreads(10);//设置openMP的线程数 我一般是10条就够了// 主要是改变这个值来看看点云的法向量的方向变换n.setViewPoint(1,1,1);//设置视点,默认为(0,0,0)n.setInputCloud(cloud);n.setSearchMethod(tree);n.setKSearch(10);//点云法向计算时,需要所搜的近邻点大小//n.setRadiusSearch(0.03);//半径搜素n.compute(*normals);//开始进行法向计//----------------可视化--------------boost::shared_ptr<pcl::visualization::PCLVisualizer> viewer(new pcl::visualization::PCLVisualizer("Normal viewer"));//viewer->initCameraParameters();//设置照相机参数,使用户从默认的角度和方向观察点云//设置背景颜色viewer->setBackgroundColor(0.3, 0.3, 0.3);viewer->addText("Normal", 10, 10, "text");//设置点云颜色pcl::visualization::PointCloudColorHandlerCustom<pcl::PointXYZ> single_color(cloud, 255, 225,255);//添加坐标系viewer->addCoordinateSystem(0.1);viewer->addPointCloud<pcl::PointXYZ>(cloud, single_color, "sample cloud");//添加需要显示的点云法向。cloud为原始点云模型,normal为法向信息,10表示需要显示法向的点云间隔,即每10个点显示一次法向,0.1表示法向长度。viewer->addPointCloudNormals<pcl::PointXYZ, pcl::Normal>(cloud, normals, 100, 0.03, "normals");//设置点云大小viewer->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 1, "sample cloud");while (!viewer->wasStopped()){viewer->spinOnce(100);boost::this_thread::sleep(boost::posix_time::microseconds(100000));}return 0;}#endif 四、算法原理
五、算法流程
相关文章:

PCL 点云匹配 之NICP(Normal ICP)
一、概述 上面一篇中我们已经得出了一个结论,就是ICP虽然简单,但是也有明显的缺点 1、计算速度慢,收敛慢,迭代次数多 2、对内存的开销比较大 3、很容易陷入局部最优的困局 因此我们在经典ICP的基础上添加一两个约束: 第…...

华脉智联融合通信一张图
随着通信技术、信息技术以及互联网的发展,融合通信技术也日益发展成熟。融合通信系统作为常见的通信指挥调度系统,其发挥的功能也越来越强大,在不同行业中的应用也越来越丰富。 华脉智联深耕融合通信行业多年,自主研发的融合通信…...

Flink系列之:窗口Top-N
Flink系列之:窗口Top-N 一、窗口Top-N二、示例:在窗口聚合后进行窗口 Top-N三、在窗口表值函数后进行窗口 Top-N四、限制 一、窗口Top-N 适用于流、批一体窗口 Top-N 是特殊的 Top-N,它返回每个分区键的每个窗口的N个最小或最大值。与普通To…...
)
【k8s】--insecure-registry详解 ( 访问仓库、https、http)
文章目录 一、--insecure-registry是什么二、如何使用--insecure-registry三、--insecure-registry的安全风险四、--insecure-registry的替代方案五、总结参考 一、–insecure-registry是什么 --insecure-registry是docker中用来设置与docker registry通信的安全限制的一个参数…...

ElementUI,修改el-cascader的默认样式
Element UI 中的下拉弹窗是通过在整个body标签末尾动态添加div实现的,所以修改样式时,必须要定义全局样式才能实现样式覆盖,那怎样才能避免全局的样式污染呢? 解决办法:通过给组件添加自定义的 popper-class 属性来避…...

外卖系统海外版:代码与美食的完美交融
在数字化时代,外卖系统海外版正引领着全球美食点餐的新潮流。不仅为用户提供了便捷的用餐服务,更通过技术创新为美食与代码之间搭建了一座桥梁。本文将探讨其中的一些技术应用,并呈现与美食完美交融的全新体验。 多语言支持代码示例 def m…...

Java代码解析:初学者的编程入门指南
💂 个人网站:【 海拥】【神级代码资源网站】【办公神器】🤟 基于Web端打造的:👉轻量化工具创作平台💅 想寻找共同学习交流的小伙伴,请点击【全栈技术交流群】 Java作为一门强大而广泛应用的编程语言&#x…...
数据结构--图
树具有灵活性,并且存在许多不同的树的应用,但是就树本身而言有一定的局限性,树只能表示层次关系,比如父子关系。而其他的比如兄弟关系只能够间接表示。 推广--- 图 图形结构中,数据元素之间的关系是任意的。 一、图…...

AXure的情景交互
目录 导语: 1.erp多样性登录界面 2.主页跳转 3.省级联动编辑 4. 下拉加载 导语: Axure是一种流行的原型设计工具,可以用来创建网站和应用程序的交互原型。通过Axure,设计师可以创建情景交互,以展示用户与系统的交…...
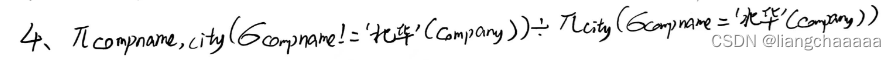
数据库操作习题12.12
考虑如下的人员数据,其中加下划线的是主码,数据库模式由四个关系组成: employee (empname, street, city) works (empname, compname, salary) company(id, compname, city) managers (empname, mgrname) 其中 关系 employee 给出人员的基本信息,包括人员…...

Redis之INCR命令,通常用于统计网站访问量,文章访问量,分布式锁
前言 Redis的INCR命令用于将键的值增加1。如果键不存在,则会先将键的值设置为0,然后再执行INCR操作。INCR命令的作用是对计数器进行自增操作,可以用于实现多种场景,比如统计网站访问量、文章访问量、分布式锁等。 一、Redis键之…...

window运行celery报错
报错信息 Traceback (most recent call last): File "c:\program files\python36\lib\site-packages\billiard\pool.py", line 359, in workloop result (True, prepare_result(fun(*args, **kwargs))) File "c:\program files\python36\lib\site-packages\ce…...

玩转Docker(五):网络
文章目录 〇、关于linux系统网络一、none网络二、host网络三、bridge网络一个问题:为什么在主机上仍可以通过localhost:port访问到容器中的服务? 四、user-defined网络 Docker安装时会自动在host上创建三个网络,我们可用docker network ls命令…...

选择合适教育管理软件:必须考虑的10个关键问题
随着教育行业的迅速数字化,学校要能够提供最新的管理和教育方法。大家逐渐意识到技术让运营变得更容易、更有效率。 不过首先我们需要找到一个能满足需求的应用程序。面对众多的选择,你该如何选择一个合适的平台呢?当然,没有人想…...

前端不同架构的分层设计
1. 架构设计分层: (1). 系统架构: ①. 应用场景:a. 应用在整个系统内,如与后台服务如何通信,与第三方系统如何集成.②. 前提条件:a. 了解前端系统与其它系统间的关系,包括业务关系和协作机制.b. 了解后端系统,需要规定与后台数据传递的机制,包括:(1). api设计规范(2). 访问授…...

android系统镜像文件
boot.img:这是包含内核和设备树(Device Tree)的镜像文件。它被引导加载程序(bootloader)加载以启动系统,并负责将控制权转交给内核。 dtbo.img:这是设备树增量编译(Device Tree Ove…...
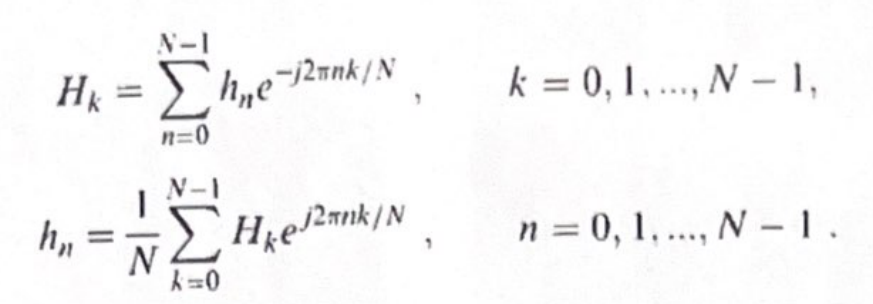
相位的重要性
在过去的几年中,相干信号和图像处理尖端技术的开发和应用有了显著的增长。相干处理的特点是使用一个称为相位的单一量[1]。相比之下,非相干处理只利用信号幅度或强度。需要进行相干处理的例子包括合成孔径雷达(SAR)、合成孔径声纳…...
补充Python经典面试题(吸收高级编程特性))
(三十三)补充Python经典面试题(吸收高级编程特性)
第一题: def func(a, b[]): pass一、上题讲解: 这个函数定义有一个默认参数b,它的默认值是一个空列表[]。这道面试题涉及到Python中函数参数默认值的一些重要概念和陷阱。 首先,当你调用这个函数时,如果不传递参数b…...

SQL进阶理论篇(四):索引的结构原理(B树与B+树)
文章目录 简介如何评价索引的数据结构设计好坏二叉树的局限性什么是B树什么是B树总结参考文献 简介 我们在上一节中说过,索引其实是一种数据结构,那它到底是一种什么样的数据结构呢?本节将简单介绍一下几个问题: 什么样的数据结…...
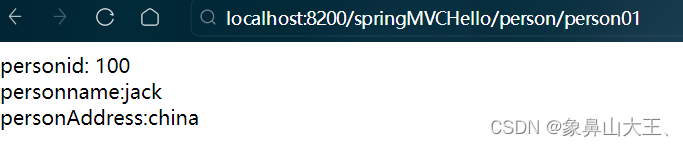
springMVC-模型数据的处理
一、数据放入到request域当中 1、把获取的数据放入request域中, 方便在跳转页面去显示 <a>添加主人信息</a> <form action"vote/vote04" method"post" >主人id:<input type"text" name"id&q…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...
