前端不同架构的分层设计
1. 架构设计分层:
(1). 系统架构:
①. 应用场景:a. 应用在整个系统内,如与后台服务如何通信,与第三方系统如何集成.②. 前提条件:a. 了解前端系统与其它系统间的关系,包括业务关系和协作机制.b. 了解后端系统,需要规定与后台数据传递的机制,包括:(1). api设计规范(2). 访问授权的一个开放标准(OAuth)跳转token的验证(3). 数据传递cookie等.c. 了解前后端关系,如前后端分离的架构设计③. 前后端分离的架构设计:a. 指的是如何实施技术决策.b. 包括:(1). 用户鉴权(2). API接口管理和设计、API文档管理(3). Mock的使用(4). BFF(服务于前端的后端、node.js)(5). 是否需要服务端渲染(6). 应用间的分层(7). 软件的性能优化(8). 代码的拆分(9). 项目的管理等
(2). 应用级架构:
①. 应用场景:a. 应用级架构可以看作系统级架构的细化.b. 单个应用与其它外部应用的关系,微服务架构下多个应用的协作、数据交换等:(1). 比如一个微前端子应用与其它子应用的交互(2). 或者单一的子应用与主应用数据交换②. 应用级架构设计的形式:a. 应用间的脚手架：用于整体应用、项目的生成b. 模式库：Utils方法库、UI库c. 设计系统：整体应用级架构内部的功能实现、与外部的信息交互等
(3). 模块级架构:
①. 应用场景:a. 开始业务编码之前进行的设计,称为迭代过程
(4). 代码级架构:
①. 规范与原则:a. 规范:(1). eslint、stylelint、htmllintb. 软件的设计原则、设计模式②. 开发流程③. 代码质量:a. 代码可维护性、可扩展性b. 简单代码可维护性高,越是抽象代码越难以维护
2. 微前端:
①. 定位:a. 应用级架构方案:(1). 在一个系统内微前端是应用间的架构方案(2). 微前端整体的子应用是应用在一个系统之间b. 系统级架构方案:(1). 对于整体的应用而言,在多个应用之间,微前端是一种系统间等架构方案(2). 微前端负责的是调度所有的子应用,不管是每个子应用的渲染、数据依赖的更新和获取、子应用的激活与卸载c. 总结:(1). 微前端是将多个前端应用以某种形式结合在一起进行应用②. 应用场景:a. 旨在解决单体应用在一个相对长的时间跨度下b. 由于参与的人员、团队的增多、变迁,从一个普通应用演变成一个巨石应用(Frontend Monolith)c. 随之而来的应用不可维护、不利于扩展的问题d. 解决方案:(1). 可以使用微前端将一个巨石应用拆解成颗粒度细的应用来进行维护
相关文章：
前端不同架构的分层设计
1. 架构设计分层: (1). 系统架构: ①. 应用场景:a. 应用在整个系统内,如与后台服务如何通信,与第三方系统如何集成.②. 前提条件:a. 了解前端系统与其它系统间的关系,包括业务关系和协作机制.b. 了解后端系统,需要规定与后台数据传递的机制,包括:(1). api设计规范(2). 访问授…...
android系统镜像文件
boot.img：这是包含内核和设备树（Device Tree）的镜像文件。它被引导加载程序（bootloader）加载以启动系统，并负责将控制权转交给内核。 dtbo.img：这是设备树增量编译（Device Tree Ove…...
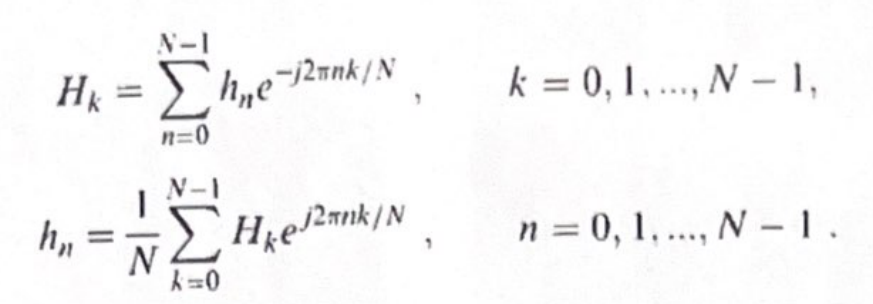
相位的重要性
在过去的几年中，相干信号和图像处理尖端技术的开发和应用有了显著的增长。相干处理的特点是使用一个称为相位的单一量[1]。相比之下，非相干处理只利用信号幅度或强度。需要进行相干处理的例子包括合成孔径雷达（SAR）、合成孔径声纳…...
（三十三）补充Python经典面试题（吸收高级编程特性）
第一题： def func(a, b[]): pass一、上题讲解： 这个函数定义有一个默认参数b，它的默认值是一个空列表[]。这道面试题涉及到Python中函数参数默认值的一些重要概念和陷阱。 首先，当你调用这个函数时，如果不传递参数b…...
SQL进阶理论篇（四）：索引的结构原理（B树与B+树）
文章目录 简介如何评价索引的数据结构设计好坏二叉树的局限性什么是B树什么是B树总结参考文献 简介 我们在上一节中说过，索引其实是一种数据结构，那它到底是一种什么样的数据结构呢？本节将简单介绍一下几个问题： 什么样的数据结…...
springMVC-模型数据的处理
一、数据放入到request域当中 1、把获取的数据放入request域中， 方便在跳转页面去显示 <a>添加主人信息</a> <form action"vote/vote04" method"post" >主人id：<input type"text" name"id&q…...
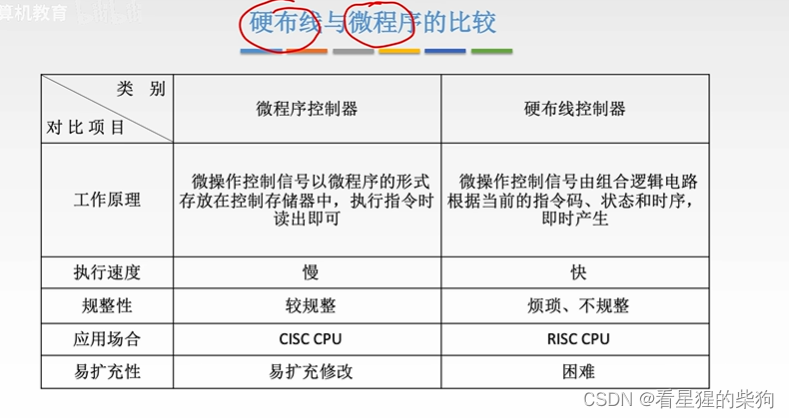
计算机组成原理-微指令的设计与微程序控制单元的设计
文章目录 微指令的设计微指令的格式微指令的编码方式水平型微指令的操作控制部分的编码方式直接编码字段直接编码例题字段间接编码方式 微指令的地址形成方式例题小结 微程序控制单元的设计微程序设计分类硬布线与微程序的比较 微指令的设计 微指令的格式 水平型微指令的操作…...
PyTorch机器学习与深度学习
近年来，随着AlphaGo、无人驾驶汽车、医学影像智慧辅助诊疗、ImageNet竞赛等热点事件的发生，人工智能迎来了新一轮的发展浪潮。尤其是深度学习技术，在许多行业都取得了颠覆性的成果。另外，近年来，Pytorch深度学习框架受…...
羊奶vs牛奶，羊大师告诉你谁是更营养的选择？
羊奶vs牛奶，羊大师告诉你谁是更营养的选择？ 羊奶和牛奶是两种常见的乳制品，它们不仅在口味上有所差异，而且在营养成分方面也存在一些差异。本文将对羊奶和牛奶的营养成分进行全面对比，旨在帮助读者更好地了解这两种乳…...
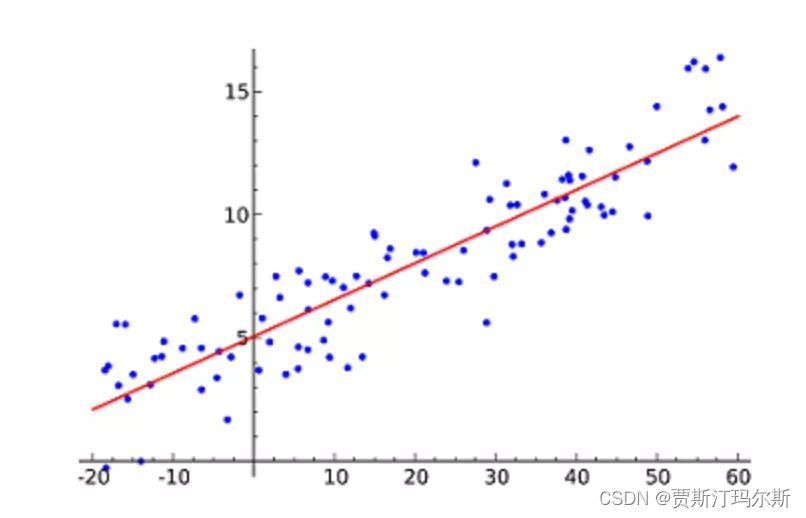
机器学习之线性回归（Linear Regression）
概念 线性回归（Linear Regression）是机器学习中的一种基本的监督学习算法，用于建立输入变量（特征）与输出变量（目标）之间的线性关系。它假设输入变量与输出变量之间存在线性关系，并试图找到最佳拟合线来描述这种关系。 在简单线性回归中，只涉及两个变量：一个是自变量…...
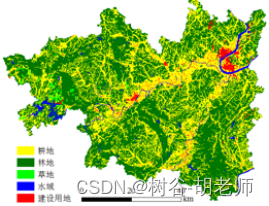
ChatGPT与ArcGIS PRO 如何结合，打造一个全新的工作流程
在地学领域，ArcGIS几乎成为了每位科研工作者作图、数据分析的必备工具，而ArcGIS Pro3除了良好地继承了ArcMap强大的数据管理、制图、空间分析等能力，还具有二三维融合、大数据、矢量切片制作及发布、任务工作流、时空立方体等特色功能&#x…...
【深度学习】对比学习的损失函数
前言 对比学习损失（Contrastive Learning Loss）是一种用于自监督学习的损失函数。它侧重于学习一个特征空间，其中相似的样本被拉近，而不相似的样本被推远。在二分类任务中，对比学习损失可以用来学习区分正负样本的特征…...
哈夫曼解码
【问题描述】 给定一组字符的Huffman编码表（从标准输入读取），给定一个用该编码表进行编码的Huffman编码文件（存在当前目录下的in.txt中），编写程序对Huffman编码文件进行解码。 例如给定的一组字符的Huffm…...
Excel小技能：excel如何将数字20231211转化成指定日期格式2023/12/11
给了一串数字20231211，想要转成指定格式的日期格式，发现设置单元格格式为指定日期格式不生效，反而变成很长很长的一串#这个，如图所示： 其实，正确的做法如下： 1）打开数据功能界面&am…...
Selenium自动化测试框架（超详细总结分享）
设计思路 本文整理归纳以往的工作中用到的东西，现汇总成基础测试框架提供分享。 框架采用python3 selenium3 PO yaml ddt unittest等技术编写成基础测试框架，能适应日常测试工作需要。 1、使用Page Object模式将页面定位和业务操作分开ÿ…...
STM32 DAC+串口
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档 文章目录 前言一、DAC是什么？二、STM32 DAC1.什么型号有DAC2. 简介3. 主要特点4. DAC框图5. DAC 电压范围和引脚 三、程序步骤1. 开启DAC时钟2. 配置引脚 PA4 PA5…...
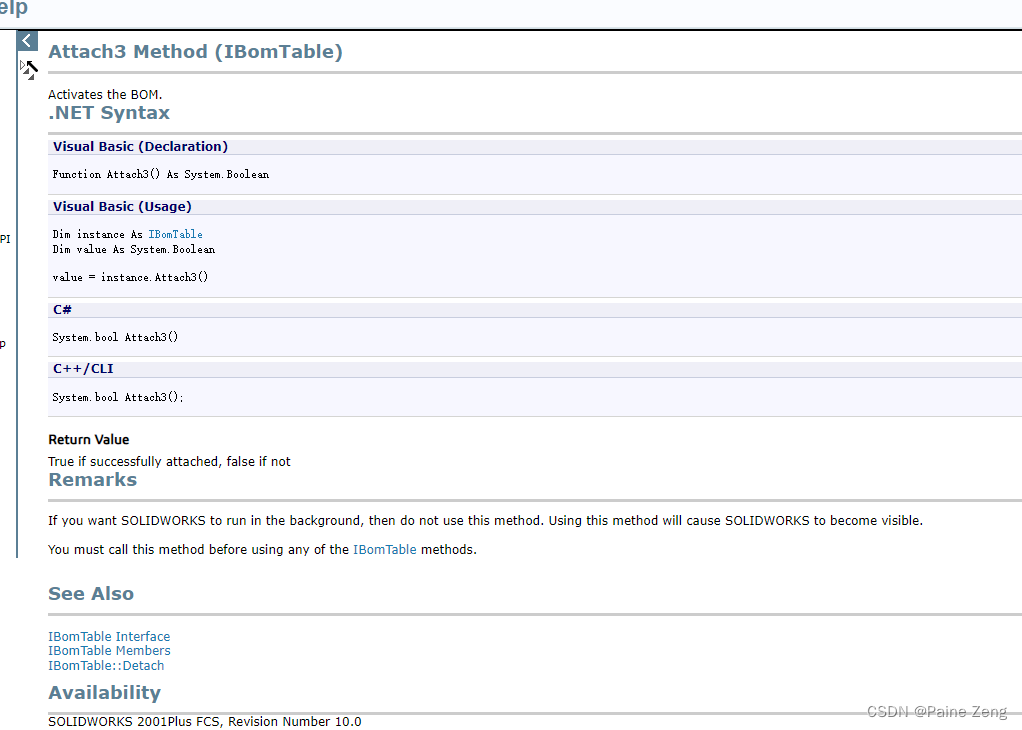
SolidWorks二次开发 C#-读取基于Excel的BOM表信息
SolidWorks二次开发 C#-读取基于Excel的BOM表信息 问题点来源解决方案及思路相关引用链接 问题点来源 这是一位粉丝问的一个问题，他说到: 老师，请问Solidworks二次开发工程图中"基于Excel的材料明细表"怎么读取里面的数据？ Ps:这…...
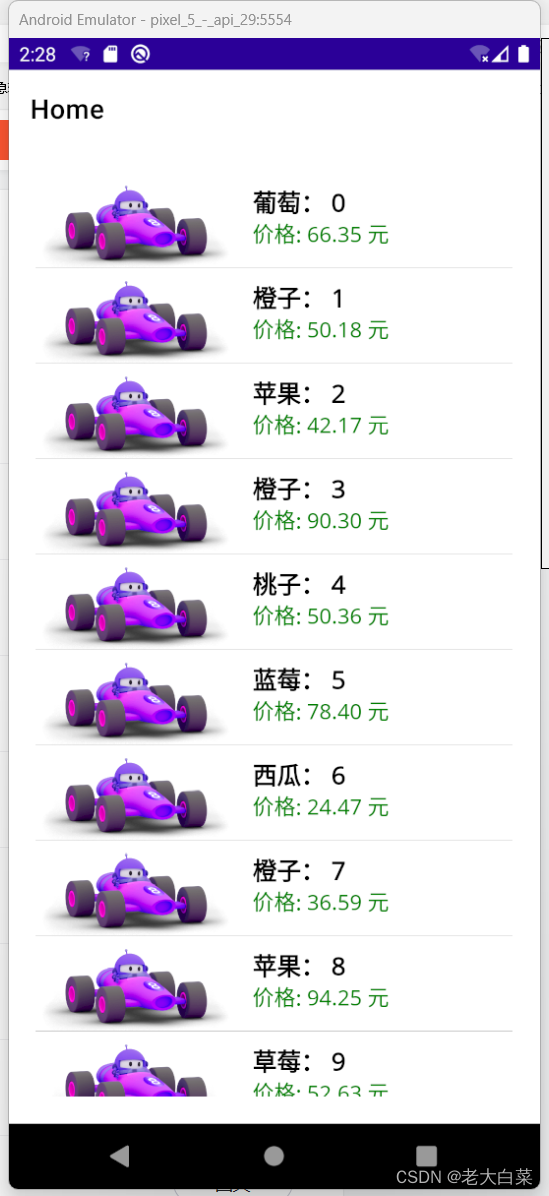
maui中实现加载更多 RefreshView跟ListView（2）
一个类似商品例表的下拉效果： 代码 新增个类为商品商体类 public class ProductItem{public string ImageSource { get; set; }public string ProductName { get; set; }public string Price { get; set; }}界面代码： <?xml version"1.0&quo…...
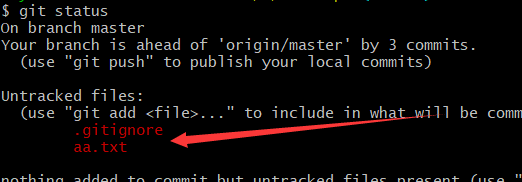
win10环境下git安装和基础操作
简述 关于git的作用就不多赘述了，配合GitHub，达到方便人们日常项目维护和管理，每一次项目增删改查都可以看的清清楚楚，方便团队协作和个人项目日常维护。 下载git 首先我们自然是要到官网下载git，下载地址为https:/…...
将yolo格式转化为voc格式：txt转xml(亲测有效)
1.文件目录如下所示： 对以上目录的解释： 1.dataset下面的image文件夹：里面装的是数据集的原图片 2.dataset下面的label文件夹：里面装的是图片对应得yolo格式标签 3.dataset下面的Annotations文件夹：这是一个空文件夹&…...
内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤： 1）请求大小调整：首先，malloc 需要调整用户请求的大小，以适应内部数据结构（例如，可能需要存储额外的元数据）。通常，这包括对齐调整，确保分配的内存地址满足特定硬件要求（如对齐到8字节或16字节边界）。 2）空闲…...
在rocky linux 9.5上在线安装 docker
前面是指南，后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...
【位运算】消失的两个数字（hard）
消失的两个数字（hard） 题⽬描述：解法（位运算）：Java 算法代码：更简便代码 题⽬链接：⾯试题 17.19. 消失的两个数字 题⽬描述： 给定⼀个数组，包含从 1 到 N 所有…...
visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中，选择 环境 -> 常规 ，将其中的颜色主题改成深色 点击确定，更改完成...
Auto-Coder使用GPT-4o完成：在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库，获取股票数据，并生成TabPFN这个模型 可以识别、处理的格式，写一个完整的预处理示例，并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务，进行预测并输…...
-----深度优先搜索（DFS）实现)
c++ 面试题(1)-----深度优先搜索（DFS）实现
操作系统：ubuntu22.04 IDE:Visual Studio Code 编程语言：C11 题目描述 地上有一个 m 行 n 列的方格，从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子，但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...
家政维修平台实战20：权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系，主要是分成几个表，用户表我们是记录用户的基础信息，包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题，不同的角色…...
linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行，YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID： YW3…...
【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类：块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...
Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式： 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...