数据结构--图
树具有灵活性,并且存在许多不同的树的应用,但是就树本身而言有一定的局限性,树只能表示层次关系,比如父子关系。而其他的比如兄弟关系只能够间接表示。
推广--- 图
图形结构中,数据元素之间的关系是任意的。
一、图的基本概念

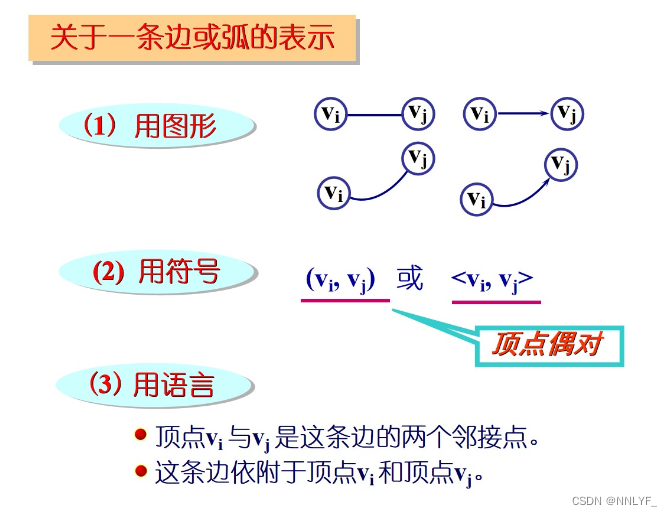
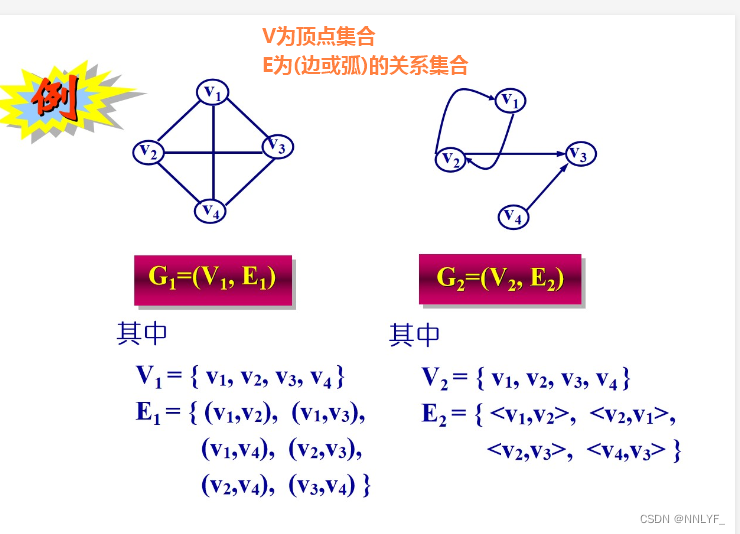
二、图的分类

三、图的相关术语
1、顶点的度

无向图:n个顶点找两条,没有方向,![]()

![]()

2、路径和路径长度
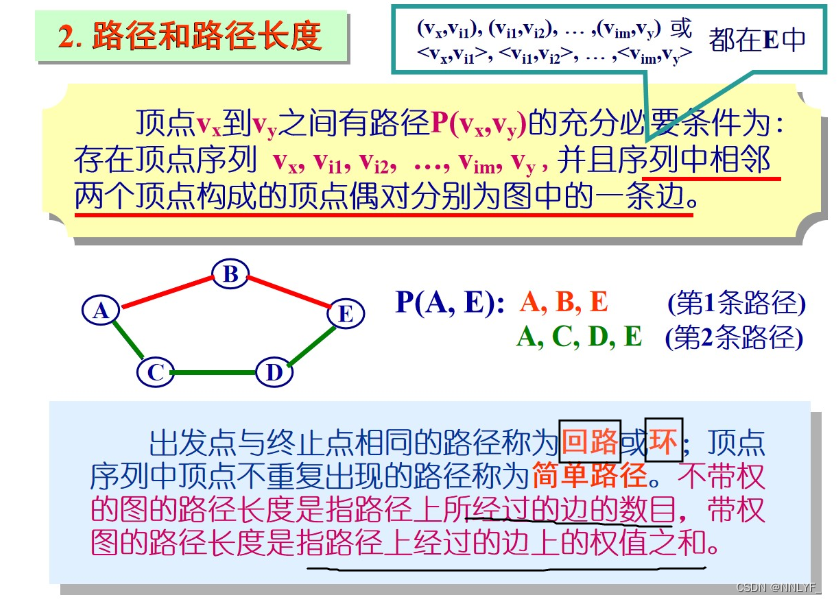
3.子图
4.图的连通
1)无向图的连通
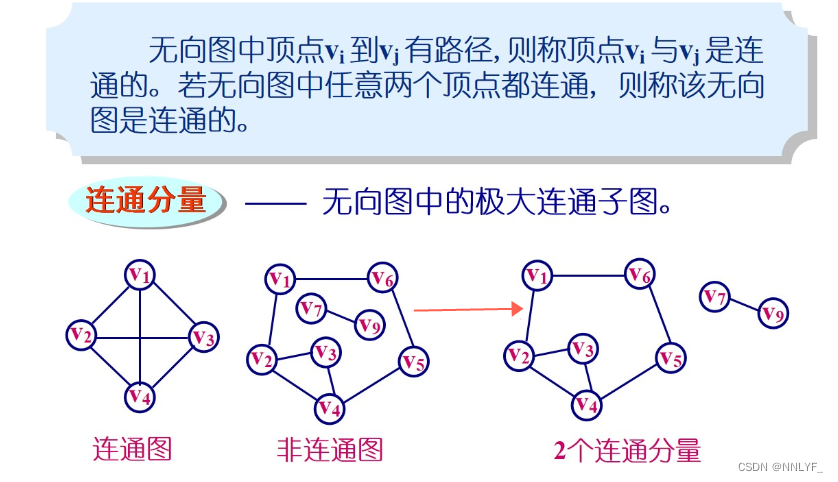
2)有向图的连通
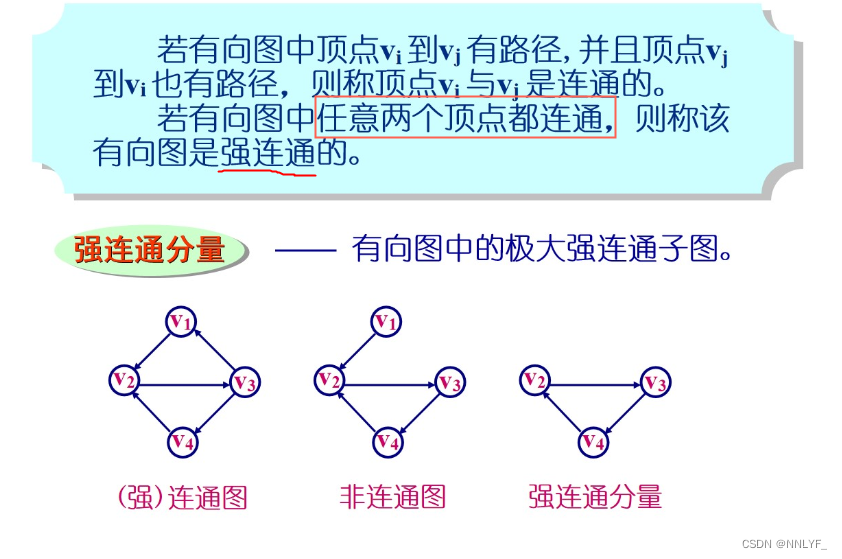

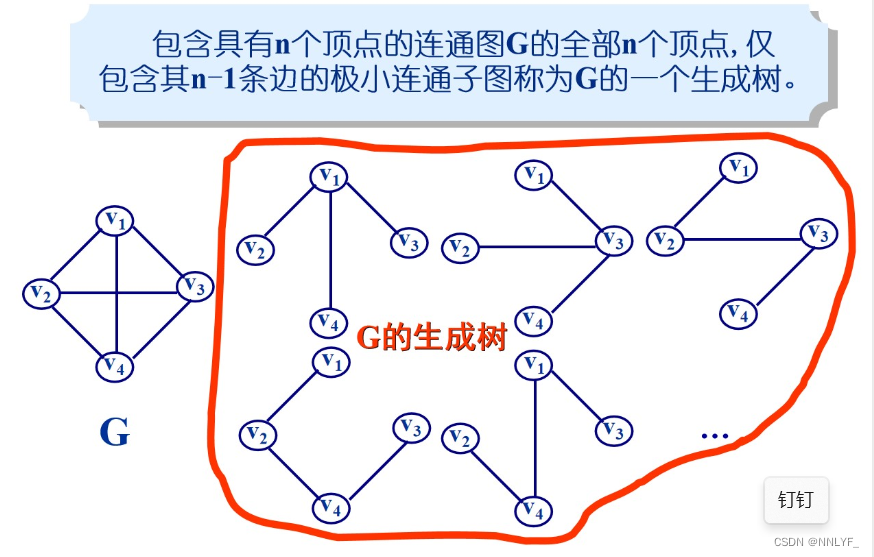
5.生成树
#不讨论的图: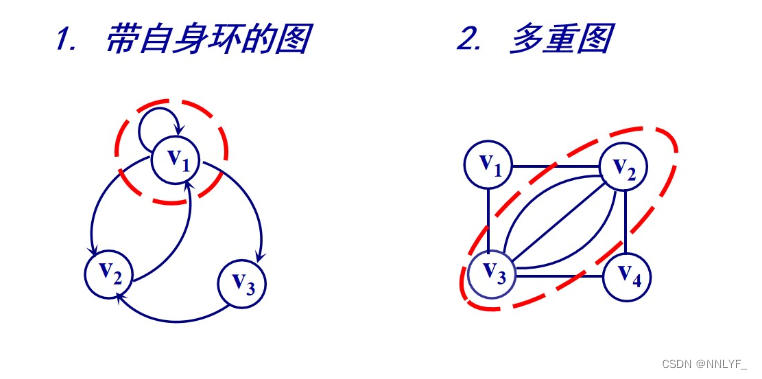
四、图的存储方法

1、邻接矩阵存储方法


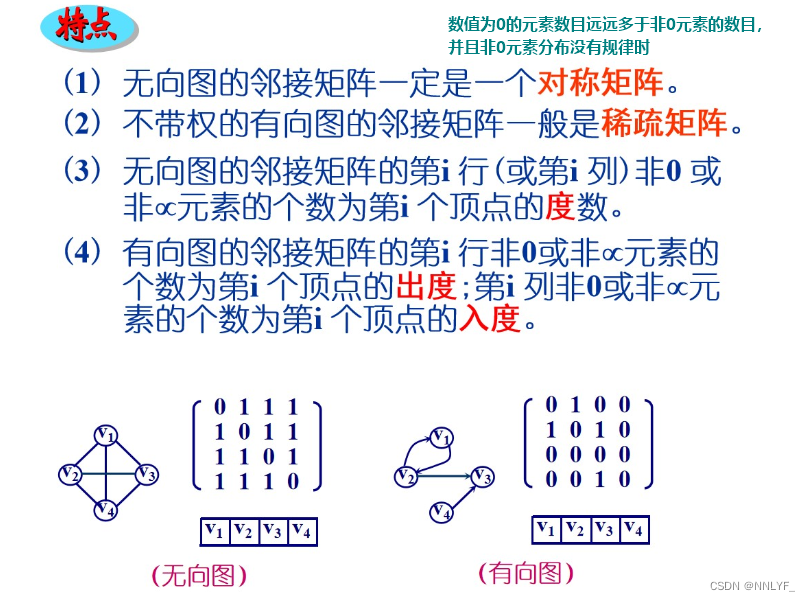
对称矩阵:
一个对称矩阵是指矩阵的主对角线两侧的元素相等。在这个矩阵中,通过观察可以发现对称性质:矩阵的第i行第j列的元素等于第j行第i列的元素。
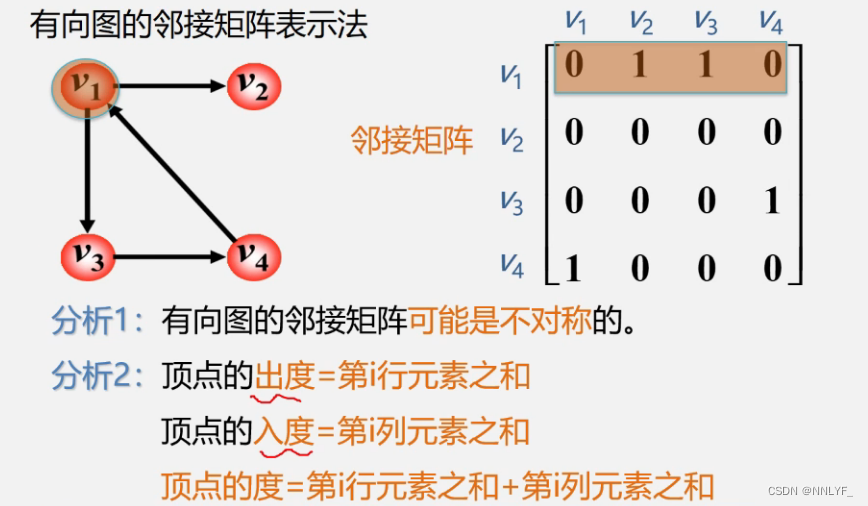
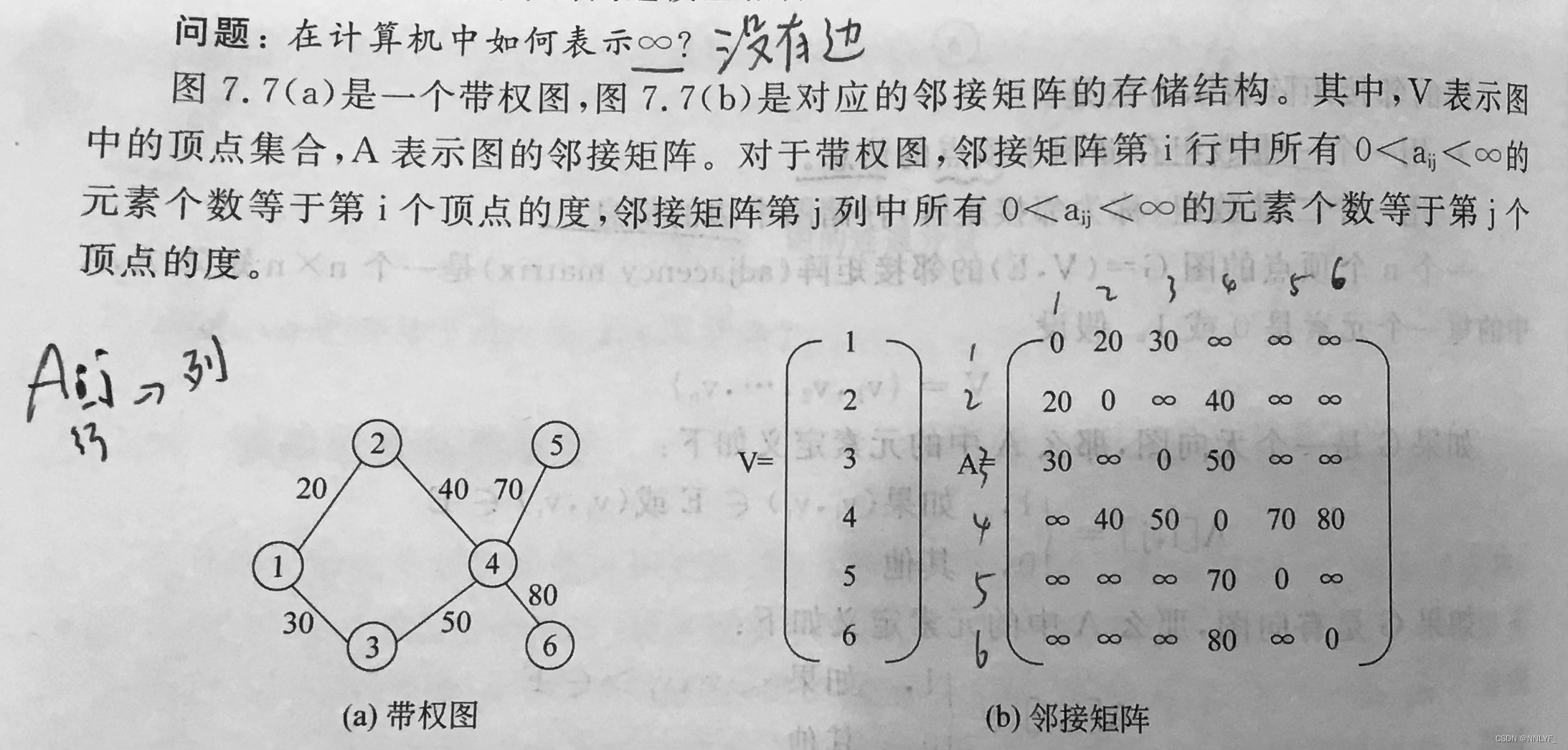
**无向图的邻接矩阵建图和度数输出(完整代码)
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <string.h>
#define N (100 + 5)
#define INF 0x3f3f3f3f//定义INF为一个十六进制无穷大常量typedef char VexType; //顶点为字符类型
typedef int EdgeType;//邻接矩阵类型为整型typedef struct {int n, m; //n个顶点,m条边VexType vex[N];//一维数组存放所有顶点的数据信息EdgeType edge[N][N];//邻接矩阵(二维数组存放图中所有顶点之间关系的信息)
} adjGraph;//1.邻接矩阵建图
adjGraph createGraph();
//2.输出图的信息(顶点、邻接矩阵)
void print(adjGraph g);
//3.输出图中每个顶点的度数
void printDegree(adjGraph g);int main()
{//1.建图adjGraph g = createGraph();//2.输出图的信息print(g);printDegree(g);return 0;
}adjGraph createGraph()//建图
{adjGraph g;memset(g.edge, 0, sizeof(g.edge));//内存设置函数--创建图的过程中,所有元素初始化为0// g.edge 邻接矩阵//sizeof(g.edge) 数组占用的总字节数scanf("%d%d", &g.n, &g.m);//输入顶点数和边数getchar();//吸收换行符//1.输入n个顶点for (int i = 0; i < g.n; i++) {scanf("%c ", &g.vex[i]);}//2.输入m条边,按照邻接矩阵存图for (int i = 0; i < g.m; i++) {char v1, v2;scanf("\n%c %c", &v1, &v2);//读入当前边的2个顶点int n1 = v1 - 'A', n2 = v2 - 'A';//将顶点字符转换为对应的数组索引。// 假设顶点标签是大写字母'A'、'B'、'C'等,通过将其减去字符'A'的ASCII码值// 可以得到对应的数组索引(0、1、2等)。 g.edge[n1][n2] = g.edge[n2][n1] = 1;//无向图,邻接矩阵对应的n1行n2列和n2n1列都赋值为1(邻接矩阵的对称性)//将对应的邻接矩阵元素设置为1,表示图中对应的顶点之间存在一条边。}return g;
}void print(adjGraph g)
{printf("图有%d个顶点,%d条边\n", g.n, g.m);printf("图的顶点是:");for (int i = 0; i < g.n; i++) {printf("%c ", g.vex[i]);}printf("\n图的邻接矩阵是:\n");for (int i = 0; i < g.n; i++) {for (int j = 0; j < g.n; j++) {printf("%4d", g.edge[i][j]);}printf("\n");}
}void printDegree(adjGraph g)
{printf("图中每个顶点的度数是:");for (int i = 0; i < g.n; i++) {int degree = 0;for (int j = 0; j < g.n; j++) {if (g.edge[i][j] == 1) {degree++;}}printf("%c: %d ", g.vex[i], degree);}printf("\n");
}
输入样例:

**有向图邻接矩阵建图和度数输出(附完整代码)
修改的部分:
- 将g.edge[n1][n2] = g.edge[n2][n1] = 1; 修改为 g.edge[n1][n2] = 1; 表示从顶点n1指向顶点n2的有向边。
- 把无向图中的度数输出改成入度和出度输出
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <string.h>
#define N (100 + 5)
#define INF 0x3f3f3f3f//定义INF为一个十六进制无穷大常量typedef char VexType; //顶点为字符类型
typedef int EdgeType;//邻接矩阵类型为整型typedef struct {int n, m; //n个顶点,m条边VexType vex[N];//一维数组存放所有顶点的数据信息EdgeType edge[N][N];//邻接矩阵(二维数组存放图中所有顶点之间关系的信息)
} adjGraph;//1.邻接矩阵建图
adjGraph createGraph();
//2.输出图的信息(顶点、邻接矩阵)
void print(adjGraph g);
//3.输出图中每个顶点的度数
void printDegree(adjGraph g);int main()
{//1.建图adjGraph g = createGraph();//2.输出图的信息print(g);printDegree(g);return 0;
}adjGraph createGraph()//建图
{adjGraph g;memset(g.edge, 0, sizeof(g.edge));//内存设置函数--创建图的过程中,所有元素初始化为0// g.edge 邻接矩阵//sizeof(g.edge) 数组占用的总字节数scanf("%d%d", &g.n, &g.m);//输入顶点数和边数getchar();//吸收换行符//1.输入n个顶点for (int i = 0; i < g.n; i++) {scanf("%c ", &g.vex[i]);}//2.输入m条边,按照邻接矩阵存图for (int i = 0; i < g.m; i++) {char v1, v2;scanf("\n%c %c", &v1, &v2);//读入当前边的2个顶点int n1 = v1 - 'A', n2 = v2 - 'A';//将顶点字符转换为对应的数组索引。// 假设顶点标签是大写字母'A'、'B'、'C'等,通过将其减去字符'A'的ASCII码值// 可以得到对应的数组索引(0、1、2等)。 g.edge[n1][n2] = 1;//有向图,邻接矩阵对应的n1行n2列赋值为1//将对应的邻接矩阵元素设置为1,表示图中对应的顶点之间存在一条边。}return g;
}void print(adjGraph g)
{printf("图有%d个顶点,%d条边\n", g.n, g.m);printf("图的顶点是:");for (int i = 0; i < g.n; i++) {printf("%c ", g.vex[i]);}printf("\n图的邻接矩阵是:\n");for (int i = 0; i < g.n; i++) {for (int j = 0; j < g.n; j++) {printf("%4d", g.edge[i][j]);}printf("\n");}
}void printDegree(adjGraph g)
{printf("图中每个顶点的入度是:\n");for (int i = 0; i < g.n; i++) {int indegree = 0;for (int j = 0; j < g.n; j++) {if (g.edge[j][i] == 1) {indegree++;}}printf("%c: %d \n", g.vex[i], indegree);}printf("图中每个顶点的出度是:\n");for (int i = 0; i < g.n; i++) {int outdegree = 0;for (int j = 0; j < g.n; j++) {if (g.edge[i][j] == 1) {outdegree++;}}printf("%c: %d \n", g.vex[i], outdegree);}}
测试样例:
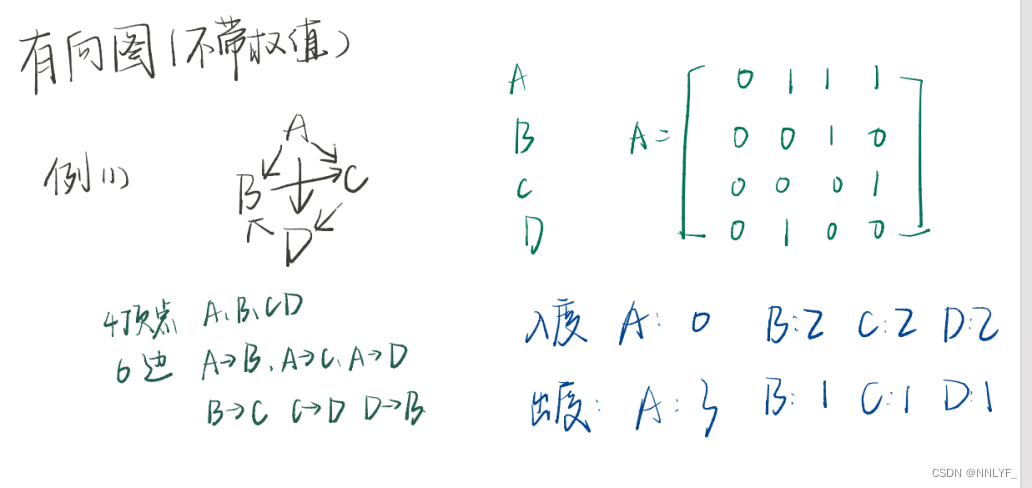

**有向带权图邻接矩阵建图和度数输出(含完整代码)


#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <string.h>
#define N (100 + 5)
#define INF 0x3f3f3f3f//定义INF为一个十六进制无穷大常量typedef char VexType; //顶点为字符类型
typedef int EdgeType;//邻接矩阵类型为整型typedef struct {int n, m; //n个顶点,m条边VexType vex[N];//一维数组存放所有顶点的数据信息EdgeType edge[N][N];//邻接矩阵(二维数组存放图中所有顶点之间关系的信息)
} adjGraph;//1.邻接矩阵建图
adjGraph createGraph();
//2.输出图的信息(顶点、邻接矩阵)
void print(adjGraph g);
//3.输出图中每个顶点的度数
void printDegree(adjGraph g);int main()
{//1.建图adjGraph g = createGraph();//2.输出图的信息print(g);printDegree(g);return 0;
}adjGraph createGraph()//建图
{adjGraph g;memset(g.edge, 0, sizeof(g.edge));//内存设置函数--创建图的过程中,所有元素初始化为0// g.edge 邻接矩阵//sizeof(g.edge) 数组占用的总字节数scanf("%d%d", &g.n, &g.m);//输入顶点数和边数getchar();//吸收换行符//1.输入n个顶点for (int i = 0; i < g.n; i++) {scanf("%c ", &g.vex[i]);}//2.输入m条边,按照邻接矩阵存图 // 将邻接矩阵初始化为INFfor (int i = 0; i < g.m; i++) {for (int j = 0; j < g.m; j++) {g.edge[i][j] = INF;}}for (int i = 0; i < g.m; i++) {char v1, v2;int weight;scanf("\n%c %d %c", &v1, &weight, &v2);//读入当前边的2个顶点int n1 = v1 - 'A', n2 = v2 - 'A';//将顶点字符转换为对应的数组索引。// 假设顶点标签是大写字母'A'、'B'、'C'等,通过将其减去字符'A'的ASCII码值// 可以得到对应的数组索引(0、1、2等)。if (n1 == n2) {g.edge[n1][n2] = 0;}else {g.edge[n1][n2] = weight;g.edge[n2][n1] = INF; // 反方向的边权值设置为INF}}return g;
}void print(adjGraph g)
{printf("图有%d个顶点,%d条边\n", g.n, g.m);printf("图的顶点是:");for (int i = 0; i < g.n; i++) {printf("%c ", g.vex[i]);}printf("\n图的邻接矩阵是:\n");for (int i = 0; i < g.n; i++) {for (int j = 0; j < g.n; j++) {if (i == j) printf("0 ");else if (g.edge[i][j] == INF){printf("INF ");}else {printf("%-4d", g.edge[i][j]);}}printf("\n");}
}void printDegree(adjGraph g)
{printf("图中每个顶点的入度是:\n");for (int i = 0; i < g.n; i++) {int indegree = 0;for (int j = 0; j < g.n; j++) {if (g.edge[j][i] != 0 && g.edge[j][i] != INF) {indegree++;}}printf("%c: %d \n", g.vex[i], indegree);}printf("图中每个顶点的出度是:\n");for (int i = 0; i < g.n; i++) {int outdegree = 0;for (int j = 0; j < g.n; j++) {if (g.edge[i][j] != 0&& g.edge[i][j] != INF) {outdegree++;}}printf("%c: %d \n", g.vex[i], outdegree);}}
样例:

2、邻接表存储方法
对每一个顶点建立一个单链表,将同一个顶点发出的边链接在一个称为边链表的单链表中。

头插法:
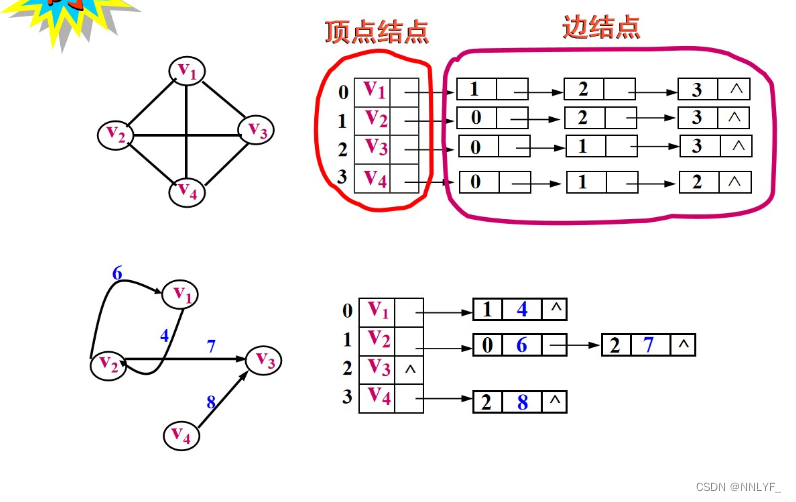

五、图的遍历


六、最小生成树
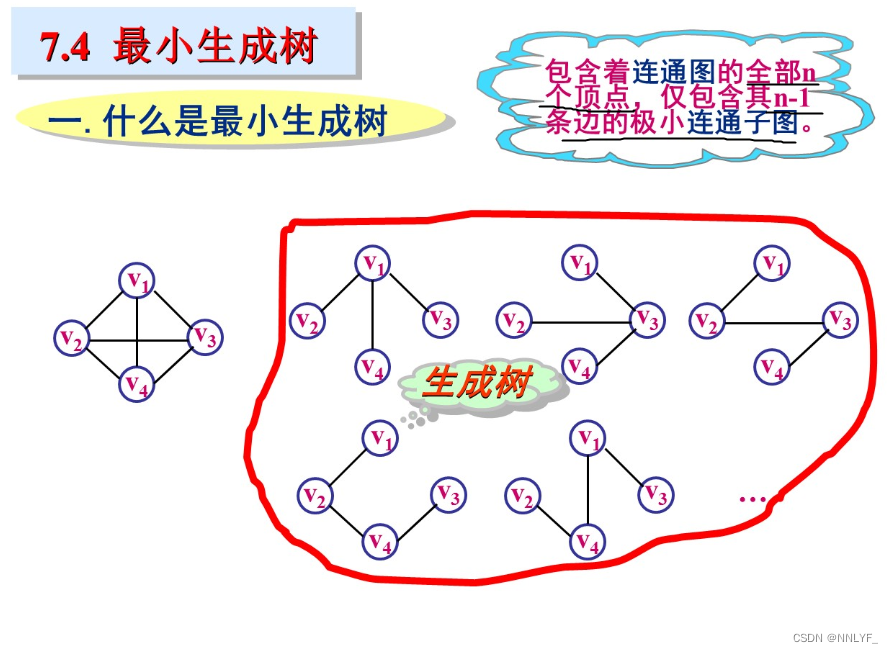
七、最短路径问题
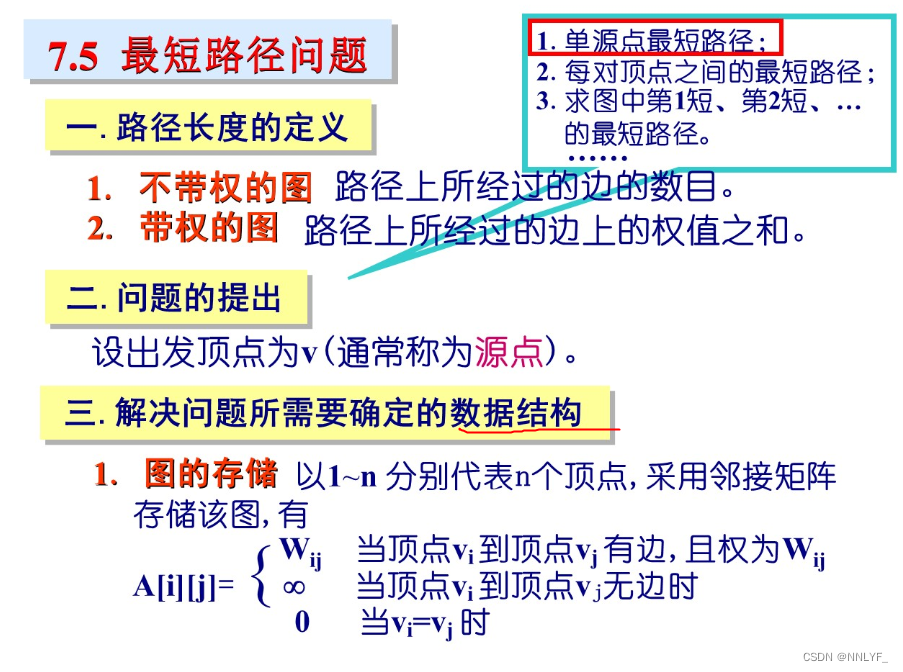
八、AOV网与拓扑排序
九、AOE网与关键路径
相关文章:

数据结构--图
树具有灵活性,并且存在许多不同的树的应用,但是就树本身而言有一定的局限性,树只能表示层次关系,比如父子关系。而其他的比如兄弟关系只能够间接表示。 推广--- 图 图形结构中,数据元素之间的关系是任意的。 一、图…...

AXure的情景交互
目录 导语: 1.erp多样性登录界面 2.主页跳转 3.省级联动编辑 4. 下拉加载 导语: Axure是一种流行的原型设计工具,可以用来创建网站和应用程序的交互原型。通过Axure,设计师可以创建情景交互,以展示用户与系统的交…...
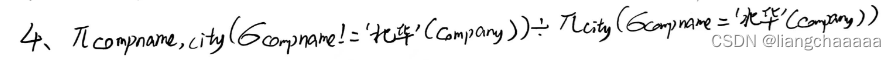
数据库操作习题12.12
考虑如下的人员数据,其中加下划线的是主码,数据库模式由四个关系组成: employee (empname, street, city) works (empname, compname, salary) company(id, compname, city) managers (empname, mgrname) 其中 关系 employee 给出人员的基本信息,包括人员…...

Redis之INCR命令,通常用于统计网站访问量,文章访问量,分布式锁
前言 Redis的INCR命令用于将键的值增加1。如果键不存在,则会先将键的值设置为0,然后再执行INCR操作。INCR命令的作用是对计数器进行自增操作,可以用于实现多种场景,比如统计网站访问量、文章访问量、分布式锁等。 一、Redis键之…...

window运行celery报错
报错信息 Traceback (most recent call last): File "c:\program files\python36\lib\site-packages\billiard\pool.py", line 359, in workloop result (True, prepare_result(fun(*args, **kwargs))) File "c:\program files\python36\lib\site-packages\ce…...

玩转Docker(五):网络
文章目录 〇、关于linux系统网络一、none网络二、host网络三、bridge网络一个问题:为什么在主机上仍可以通过localhost:port访问到容器中的服务? 四、user-defined网络 Docker安装时会自动在host上创建三个网络,我们可用docker network ls命令…...

选择合适教育管理软件:必须考虑的10个关键问题
随着教育行业的迅速数字化,学校要能够提供最新的管理和教育方法。大家逐渐意识到技术让运营变得更容易、更有效率。 不过首先我们需要找到一个能满足需求的应用程序。面对众多的选择,你该如何选择一个合适的平台呢?当然,没有人想…...

前端不同架构的分层设计
1. 架构设计分层: (1). 系统架构: ①. 应用场景:a. 应用在整个系统内,如与后台服务如何通信,与第三方系统如何集成.②. 前提条件:a. 了解前端系统与其它系统间的关系,包括业务关系和协作机制.b. 了解后端系统,需要规定与后台数据传递的机制,包括:(1). api设计规范(2). 访问授…...

android系统镜像文件
boot.img:这是包含内核和设备树(Device Tree)的镜像文件。它被引导加载程序(bootloader)加载以启动系统,并负责将控制权转交给内核。 dtbo.img:这是设备树增量编译(Device Tree Ove…...
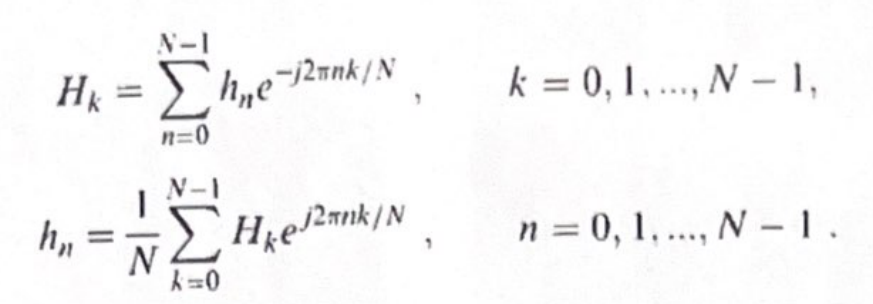
相位的重要性
在过去的几年中,相干信号和图像处理尖端技术的开发和应用有了显著的增长。相干处理的特点是使用一个称为相位的单一量[1]。相比之下,非相干处理只利用信号幅度或强度。需要进行相干处理的例子包括合成孔径雷达(SAR)、合成孔径声纳…...
补充Python经典面试题(吸收高级编程特性))
(三十三)补充Python经典面试题(吸收高级编程特性)
第一题: def func(a, b[]): pass一、上题讲解: 这个函数定义有一个默认参数b,它的默认值是一个空列表[]。这道面试题涉及到Python中函数参数默认值的一些重要概念和陷阱。 首先,当你调用这个函数时,如果不传递参数b…...

SQL进阶理论篇(四):索引的结构原理(B树与B+树)
文章目录 简介如何评价索引的数据结构设计好坏二叉树的局限性什么是B树什么是B树总结参考文献 简介 我们在上一节中说过,索引其实是一种数据结构,那它到底是一种什么样的数据结构呢?本节将简单介绍一下几个问题: 什么样的数据结…...
springMVC-模型数据的处理
一、数据放入到request域当中 1、把获取的数据放入request域中, 方便在跳转页面去显示 <a>添加主人信息</a> <form action"vote/vote04" method"post" >主人id:<input type"text" name"id&q…...
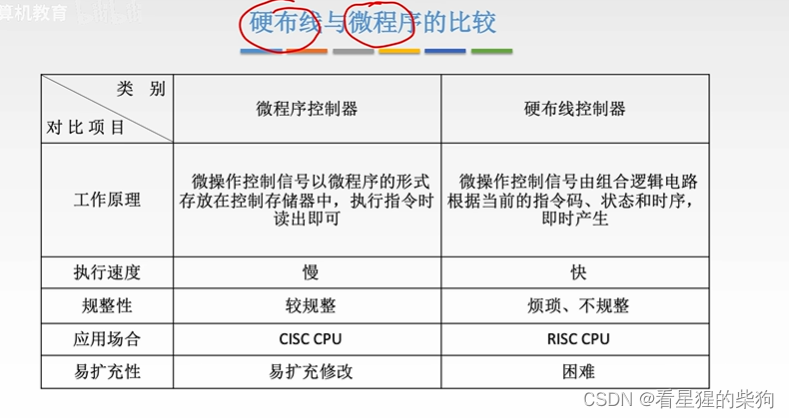
计算机组成原理-微指令的设计与微程序控制单元的设计
文章目录 微指令的设计微指令的格式微指令的编码方式水平型微指令的操作控制部分的编码方式直接编码字段直接编码例题字段间接编码方式 微指令的地址形成方式例题小结 微程序控制单元的设计微程序设计分类硬布线与微程序的比较 微指令的设计 微指令的格式 水平型微指令的操作…...

PyTorch机器学习与深度学习
近年来,随着AlphaGo、无人驾驶汽车、医学影像智慧辅助诊疗、ImageNet竞赛等热点事件的发生,人工智能迎来了新一轮的发展浪潮。尤其是深度学习技术,在许多行业都取得了颠覆性的成果。另外,近年来,Pytorch深度学习框架受…...

羊奶vs牛奶,羊大师告诉你谁是更营养的选择?
羊奶vs牛奶,羊大师告诉你谁是更营养的选择? 羊奶和牛奶是两种常见的乳制品,它们不仅在口味上有所差异,而且在营养成分方面也存在一些差异。本文将对羊奶和牛奶的营养成分进行全面对比,旨在帮助读者更好地了解这两种乳…...
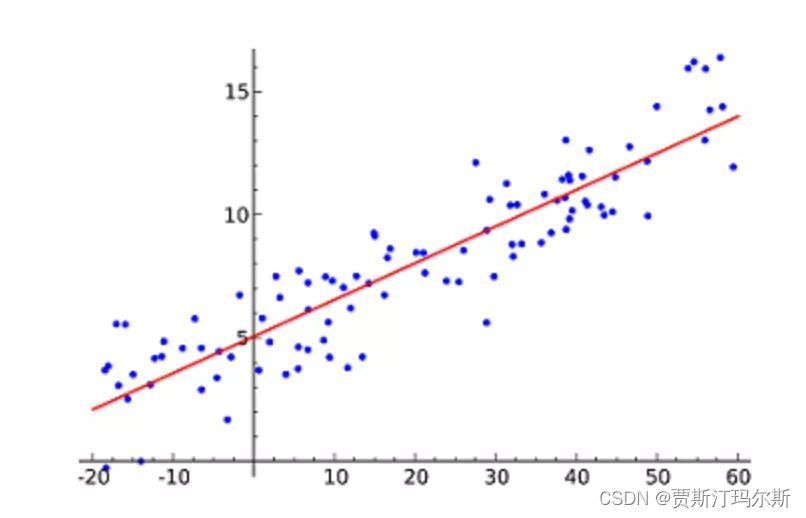
机器学习之线性回归(Linear Regression)
概念 线性回归(Linear Regression)是机器学习中的一种基本的监督学习算法,用于建立输入变量(特征)与输出变量(目标)之间的线性关系。它假设输入变量与输出变量之间存在线性关系,并试图找到最佳拟合线来描述这种关系。 在简单线性回归中,只涉及两个变量:一个是自变量…...
ChatGPT与ArcGIS PRO 如何结合,打造一个全新的工作流程
在地学领域,ArcGIS几乎成为了每位科研工作者作图、数据分析的必备工具,而ArcGIS Pro3除了良好地继承了ArcMap强大的数据管理、制图、空间分析等能力,还具有二三维融合、大数据、矢量切片制作及发布、任务工作流、时空立方体等特色功能&#x…...

【深度学习】对比学习的损失函数
前言 对比学习损失(Contrastive Learning Loss)是一种用于自监督学习的损失函数。它侧重于学习一个特征空间,其中相似的样本被拉近,而不相似的样本被推远。在二分类任务中,对比学习损失可以用来学习区分正负样本的特征…...

哈夫曼解码
【问题描述】 给定一组字符的Huffman编码表(从标准输入读取),给定一个用该编码表进行编码的Huffman编码文件(存在当前目录下的in.txt中),编写程序对Huffman编码文件进行解码。 例如给定的一组字符的Huffm…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...



