【每日一题】反转二叉树的奇数层
文章目录
- Tag
- 题目来源
- 题目解读
- 解题思路
- 方法一:广度优先搜索
- 方法二:深度优先搜索
- 写在最后
Tag
【深度优先搜索】【广度优先搜索】【二叉树】【2023-12-15】
题目来源
2415. 反转二叉树的奇数层

题目解读
反转二叉树奇数层的节点。
解题思路
对于二叉树中的节点反转,我们只需要交换节点的值。通常有广度优先搜索和深度优先搜索两种解决方法。
方法一:广度优先搜索
思路
按层遍历二叉树,将奇数层的节点都记录下来,如果当前的层是奇数层,就交换节点数组中的节点。
算法
在具体实现中,通过维护一个 bool 变量 isOdd 来记录当前层是否是奇数层。初始化 isOdd = false,因为广搜从根节点开始,这一层是 0 层当做偶数层。每遍历完一层之后更新 isOdd = !isOdd,下方实现中使用的是异或运算来更改 isOdd。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* reverseOddLevels(TreeNode* root) {queue<TreeNode*> q;q.push(root);bool isOdd = false;while (!q.empty()) {int sz = q.size();vector<TreeNode*> arr;for (int i = 0; i < sz; ++i) {TreeNode* node = q.front();q.pop();if (isOdd) {arr.push_back(node);}if (node->left) { // 完美二叉树,有左子树一定也有右子树q.push(node->left);q.push(node->right);}}if (isOdd) {for (int l = 0, r = sz - 1; l < r; ++l, --r) {swap(arr[l]->val, arr[r]->val);}}isOdd ^= true;}return root;}
};
复杂度分析
时间复杂度: O ( n ) O(n) O(n), n n n 是二叉树中节点个数,每个节点都要被遍历一次。
空间复杂度: O ( n ) O(n) O(n),用数组记录二叉树的每一层的节点数,某一层最多有 ⌈ n 2 ⌉ \lceil{\frac{n}{2}}\rceil ⌈2n⌉ 个节点,因此空间复杂度为 O ( n ) O(n) O(n)。
方法二:深度优先搜索
思路
核心依然是交换值,通过递归左右子树实现。
算法
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void dfs(TreeNode* root1, TreeNode* root2, bool isOdd) {if (root1 == nullptr) {return;}if (isOdd) {swap(root1->val, root2->val);}dfs(root1->left, root2->right, !isOdd);dfs(root1->right, root2->left, !isOdd);}TreeNode* reverseOddLevels(TreeNode* root) {dfs(root->left, root->right, true);return root;}
};
复杂度分析
时间复杂度: O ( n ) O(n) O(n), n n n 是二叉树中节点个数,每个节点都要被遍历一次。
空间复杂度: O ( l o g n ) O(logn) O(logn)。
写在最后
如果您发现文章有任何错误或者对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度的方法,欢迎评论区交流。
最后,感谢您的阅读,如果有所收获的话可以给我点一个 👍 哦。
相关文章:

【每日一题】反转二叉树的奇数层
文章目录 Tag题目来源题目解读解题思路方法一:广度优先搜索方法二:深度优先搜索 写在最后 Tag 【深度优先搜索】【广度优先搜索】【二叉树】【2023-12-15】 题目来源 2415. 反转二叉树的奇数层 题目解读 反转二叉树奇数层的节点。 解题思路 对于二叉…...

vue 项目配置反向代理导致项目白屏
问题:vue 项目配置反向代理导致项目白屏 一、现象描述 添加反向代理代码后,前端运行白屏 // 设置baseURL,8888是后端端口号,前端请求默认发送到baseURL的地址 var axios require(axios) axios.defaults.baseURL http://local…...

全国县级行政区点位数据,Shp+excel格式
基本信息. 数据名称: 县级行政区点位 数据格式: Shpexcel 数据时间: 2021年 数据几何类型: 点 数据坐标系: WGS84坐标系 数据来源:网络公开数据 数据字段: 序号字段名称字段说明1xzqhdm_1省代码2xzqhmc_1省名称3xzqhdm_2市代码4xzqhmc_2市代…...

文件包含的提升刷题
上一篇文章:一篇文章带你入门文件包含-CSDN博客 已经开始入门了文件包含,那现在开始拔高提升刷题! 1. 拿到题目后啥也没有,所以也不知道要读取啥文件,那就查看源代码。 直接看if的条件就可以知道一定要设置cookie&a…...

入门级银行测试岗位招聘,只需具备这些基本条件!
2023年应该说是超乎意外的寒冷,几乎算是百业凋零。充斥在各个地方各个行业的,更多的是裁员的消息,很少有以往的风风火火的招聘了。无论是金九银十还是在以往的淡季。 谁也不知道这样一个特殊的寒冬还有多久才能过去。但是无论面对什么样的局…...

组里新来了个00后,真卷不过....
📢专注于分享软件测试干货内容,欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正!📢交流讨论:欢迎加入我们一起学习!📢资源分享:耗时200小时精选的「软件测试」资…...

python 命令添加参数
官网 argparse模块可以很容易地编写用户友好的命令行界面。程序定义它需要什么参数,argparse将找出如何从sys.argv中解析这些参数。argparse模块还会自动生成帮助和用法消息。当用户为程序提供无效参数时,该模块也会发出错误。 核心功能 argparse模块对…...

LVS负载均衡器(DR模式)+nginx七层代理+tomcat多实例+php+mysql 实现负载均衡以及动静分离、数据库的调用!!!
目录 前言 一、nfs共享存储,为两个节点服务器提供静态网页共享 二、nginx作为lvs的后端节点服务器,完成lo:0网卡配置,以及内核参数设置,还有设置路由表 步骤一:先完成nfs共享存储挂载 步骤二:完成lo:0网…...
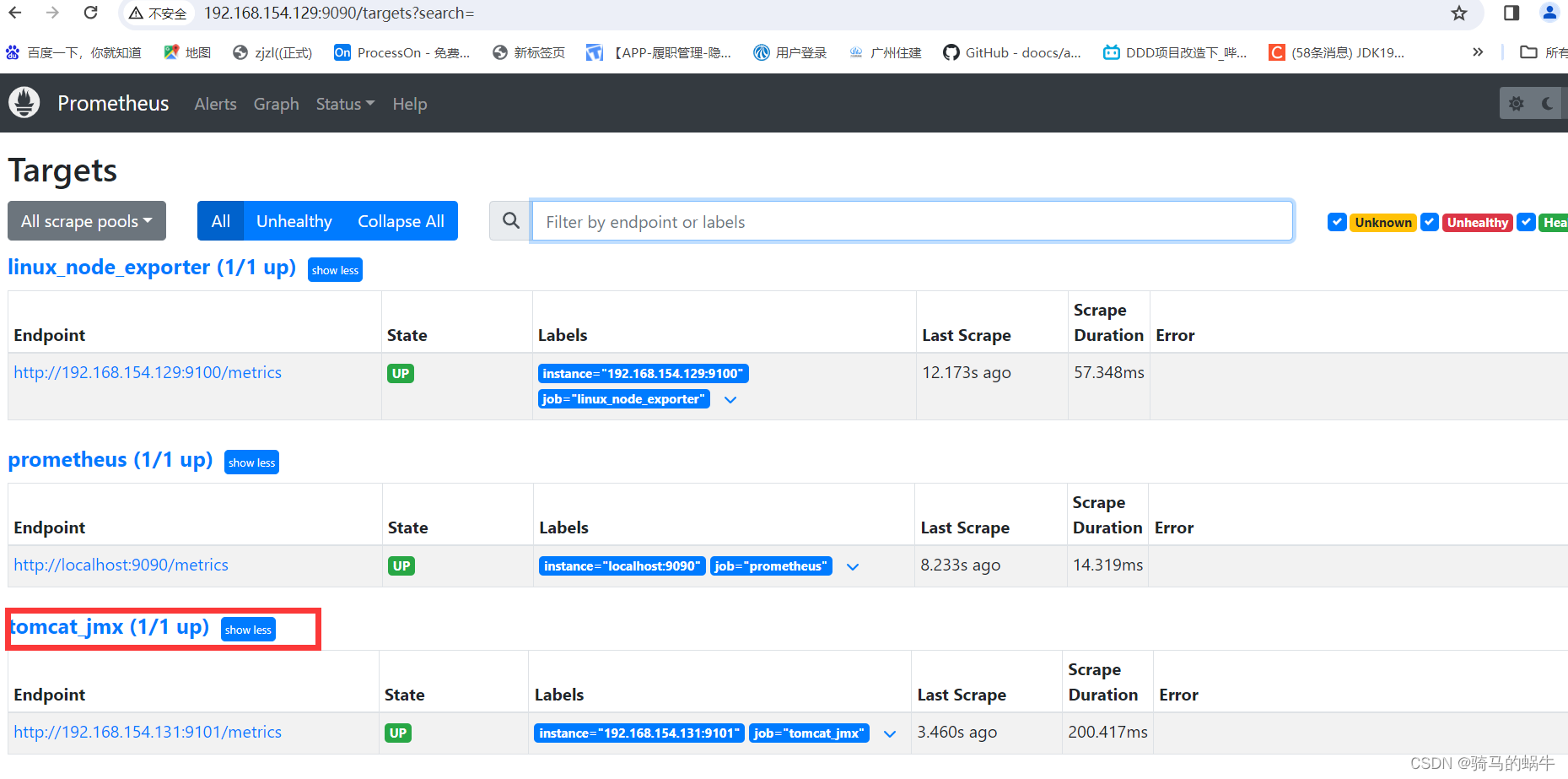
jmx_exporter安装
下载 wget https://repo1.maven.org/maven2/io/prometheus/jmx/jmx_prometheus_javaagent/0.13.0/jmx_prometheus_javaagent-0.13.0.jar 创建jmx_exporter.yml文件 文件内容为: rules: - pattern: ".*" 配置tomcatpinter/apache-tomcat-8.5.38/bin/ca…...
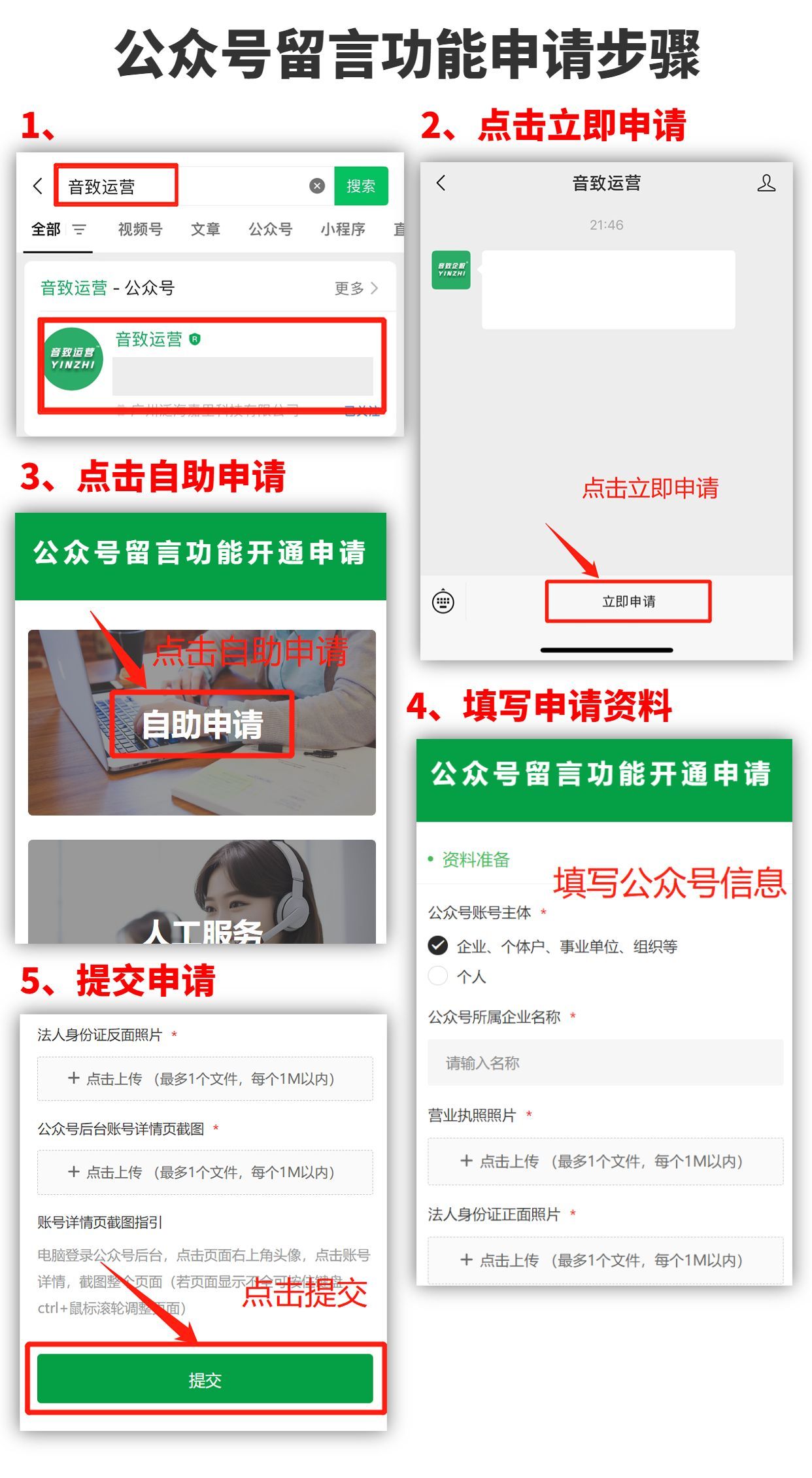
怎么给自己的微信公众号留言?
为什么公众号没有留言功能?根据要求,自2018年2月12日起,新申请的微信公众号默认无留言功能。有些人听过一个说法:公众号粉丝累计到一定程度或者原创文章数量累计到一定程度就可以开通留言功能。其实这个方法是2018年之前才可以&am…...

Unity中 URP 下的棋盘格Shader
文章目录 前言一、制作思路法1:使用纹理采样后,修改重铺效果法2:计算实现 二、粗略计算实现棋盘格效果1、使 uv.x < 0.5 区域 0 。反之, 0.52、使 uv.y < 0.5 区域 0 。反之, 0.53、使两个颜色相加4、取小数…...

杰发科技AC7840——SPM电源管理之低功耗模式
0、SPM简介 很早以前就听过低功耗模式,一直没有怎么深入了解,最近遇到几个项目都是跟低功耗有关。正好AutoChips的芯片都有电源管理的功能,在此借用AC7840的SPM对低功耗进行测试。 1、AC7840的5种功耗模式 2、AC7840的模式转换 3、唤醒 在…...
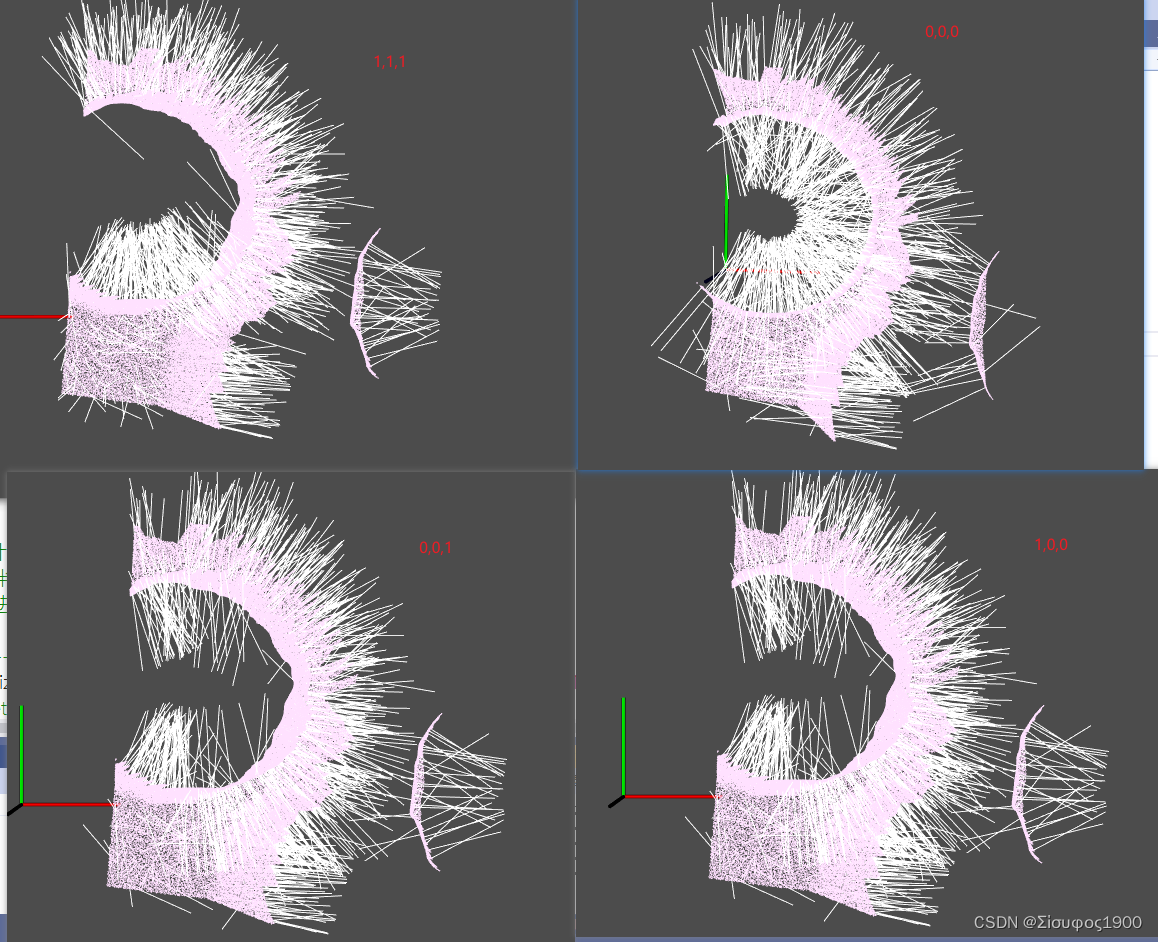
PCL 点云匹配 之NICP(Normal ICP)
一、概述 上面一篇中我们已经得出了一个结论,就是ICP虽然简单,但是也有明显的缺点 1、计算速度慢,收敛慢,迭代次数多 2、对内存的开销比较大 3、很容易陷入局部最优的困局 因此我们在经典ICP的基础上添加一两个约束: 第…...

华脉智联融合通信一张图
随着通信技术、信息技术以及互联网的发展,融合通信技术也日益发展成熟。融合通信系统作为常见的通信指挥调度系统,其发挥的功能也越来越强大,在不同行业中的应用也越来越丰富。 华脉智联深耕融合通信行业多年,自主研发的融合通信…...

Flink系列之:窗口Top-N
Flink系列之:窗口Top-N 一、窗口Top-N二、示例:在窗口聚合后进行窗口 Top-N三、在窗口表值函数后进行窗口 Top-N四、限制 一、窗口Top-N 适用于流、批一体窗口 Top-N 是特殊的 Top-N,它返回每个分区键的每个窗口的N个最小或最大值。与普通To…...
)
【k8s】--insecure-registry详解 ( 访问仓库、https、http)
文章目录 一、--insecure-registry是什么二、如何使用--insecure-registry三、--insecure-registry的安全风险四、--insecure-registry的替代方案五、总结参考 一、–insecure-registry是什么 --insecure-registry是docker中用来设置与docker registry通信的安全限制的一个参数…...

ElementUI,修改el-cascader的默认样式
Element UI 中的下拉弹窗是通过在整个body标签末尾动态添加div实现的,所以修改样式时,必须要定义全局样式才能实现样式覆盖,那怎样才能避免全局的样式污染呢? 解决办法:通过给组件添加自定义的 popper-class 属性来避…...

外卖系统海外版:代码与美食的完美交融
在数字化时代,外卖系统海外版正引领着全球美食点餐的新潮流。不仅为用户提供了便捷的用餐服务,更通过技术创新为美食与代码之间搭建了一座桥梁。本文将探讨其中的一些技术应用,并呈现与美食完美交融的全新体验。 多语言支持代码示例 def m…...

Java代码解析:初学者的编程入门指南
💂 个人网站:【 海拥】【神级代码资源网站】【办公神器】🤟 基于Web端打造的:👉轻量化工具创作平台💅 想寻找共同学习交流的小伙伴,请点击【全栈技术交流群】 Java作为一门强大而广泛应用的编程语言&#x…...
数据结构--图
树具有灵活性,并且存在许多不同的树的应用,但是就树本身而言有一定的局限性,树只能表示层次关系,比如父子关系。而其他的比如兄弟关系只能够间接表示。 推广--- 图 图形结构中,数据元素之间的关系是任意的。 一、图…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

Vue ③-生命周期 || 脚手架
生命周期 思考:什么时候可以发送初始化渲染请求?(越早越好) 什么时候可以开始操作dom?(至少dom得渲染出来) Vue生命周期: 一个Vue实例从 创建 到 销毁 的整个过程。 生命周期四个…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...

ArcGIS Pro+ArcGIS给你的地图加上北回归线!
今天来看ArcGIS Pro和ArcGIS中如何给制作的中国地图或者其他大范围地图加上北回归线。 我们将在ArcGIS Pro和ArcGIS中一同介绍。 1 ArcGIS Pro中设置北回归线 1、在ArcGIS Pro中初步设置好经纬格网等,设置经线、纬线都以10间隔显示。 2、需要插入背会归线…...
