计算 N*4*4 位姿形状的逆变换,在N*3*4位姿后补充 [0,0,0,1]
针对 [N,4,4] shape 的 poses,函数 ComputeInversePoses 返回 相同 shape,但是每个 pose 都是前面的 逆 pose。
针对 [N,3,4] shape 的 poses,函数 AddIdentityToPoses 返回 在每个 [3,4] pose下加上 [0,0,0,1] 后的pose,返回的 shape [N,4,4]
def ComputeInversePoses(poses):if isinstance(poses, torch.Tensor):# Convert torch tensor to numpy arrayposes = poses.numpy()# Check if poses is a numpy arrayif not isinstance(poses, np.ndarray):raise ValueError("Input poses must be a numpy array")# Check if poses is 3-dimensionalif len(poses.shape) != 3 or poses.shape[1:] != (4, 4):raise ValueError("Input poses must be a 3-dimensional array with shape (N, 4, 4)")# Create an array to store the inverse posesinverse_poses = np.zeros_like(poses)# Compute the inverse for each 4x4 matrixfor i in range(poses.shape[0]):inverse_poses[i] = np.linalg.inv(poses[i])return inverse_poses.astype(np.float32)def AddIdentityToPoses(poses):# Check if poses is a torch tensorif isinstance(poses, torch.Tensor):# Convert torch tensor to numpy arrayposes = poses.numpy()# Check if poses is 3-dimensionalif len(poses.shape) != 3 or poses.shape[2] != 4:raise ValueError("Input poses must be a 3-dimensional array with shape (N, 3, 4)")# Create poses_with_identity arrayposes_with_identity = np.zeros((poses.shape[0], 4, 4), dtype=np.float32)poses_with_identity[:, :3, :4] = posesposes_with_identity[:, 3, :] = [0, 0, 0, 1]return poses_with_identity.astype(np.float32)
相关文章:

计算 N*4*4 位姿形状的逆变换,在N*3*4位姿后补充 [0,0,0,1]
针对 [N,4,4] shape 的 poses,函数 ComputeInversePoses 返回 相同 shape,但是每个 pose 都是前面的 逆 pose。 针对 [N,3,4] shape 的 poses,函数 AddIdentityToPoses 返回 在每个 [3,4] pose下加上 [0,0,0,1] 后的pose,返回的…...
人工智能可以战胜人类智慧大脑么?
引言 在当今快速发展的科技时代,人工智能的进步日新月异,引发了一场深刻的讨论:能否有一天,人工智能能够超越甚至战胜人类智慧?这个问题涉及到人类认知的广泛领域,牵涉到人类思维的深层次特质以及AI技术在…...

【数据结构和算法】 K 和数对的最大数目
其他系列文章导航 Java基础合集数据结构与算法合集 设计模式合集 多线程合集 分布式合集 ES合集 文章目录 其他系列文章导航 文章目录 前言 一、题目描述 二、题解 2.1 方法一:双指针排序 三、代码 3.1 方法一:双指针排序 3.2 方法二࿱…...
基于ssm高校推免报名系统源码和论文
网络的广泛应用给生活带来了十分的便利。所以把高校推免报名管理与现在网络相结合,利用java技术建设高校推免报名管理系统,实现高校推免报名的信息化。则对于进一步提高高校推免报名管理发展,丰富高校推免报名管理经验能起到不少的促进作用。…...
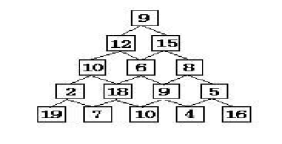
算法设计与分析2023秋-头歌实验-实验七 动态规划
文章目录 第1关:数塔问题任务描述相关知识编程要求解题思路测试说明参考答案 第2关:最长公共子序列任务描述相关知识编程要求解题思路:测试说明参考答案 第3关:求序列-2 11 -4 13 -5 -2的最大子段和任务描述相关知识编程要求解题思…...

复杂 SQL 实现分组分情况分页查询
其他系列文章导航 Java基础合集数据结构与算法合集 设计模式合集 多线程合集 分布式合集 ES合集 文章目录 其他系列文章导航 文章目录 前言 一、根据 camp_status 字段分为 6 种情况 1.1 SQL语句 1.2 SQL解释 二、分页 SQL 实现 2.1 SQL语句 2.2 根据 camp_type 区分返…...

JavaScript---如何完美的判断返回对象是否有值
如何判断一个对象为空是我们在开发中经常会遇到的问题,今天我们来聊聊几种经常使用的方法,以及在不同的场景下我们如何去使用。 1. JSON.stringify JSON.stringify 方法可以使对象序列化,转为相应的 JSON 格式。 js 复制代码 const obj {…...
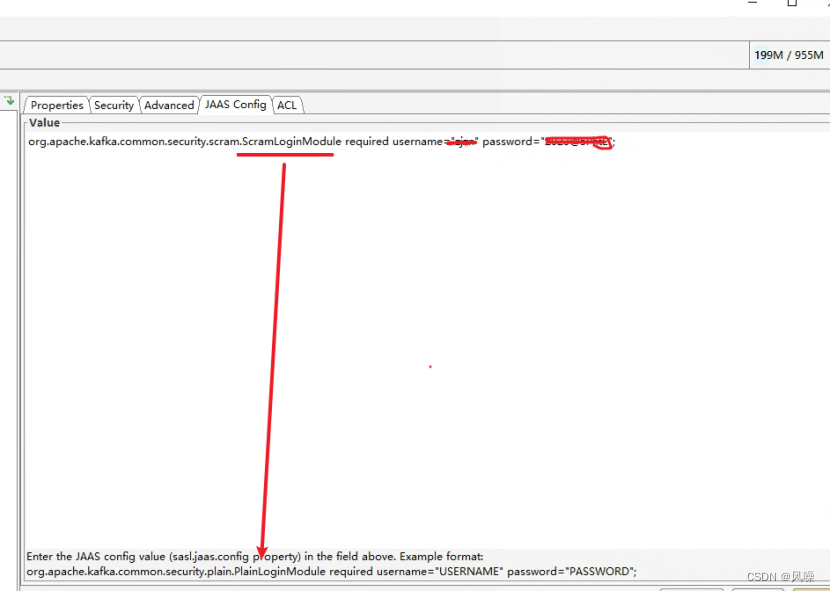
kafka offset sasl加密连接
kafka-tool(offset) 进行SCRAM连接,直接上图 填写jaas的认证(账密 引用包)...
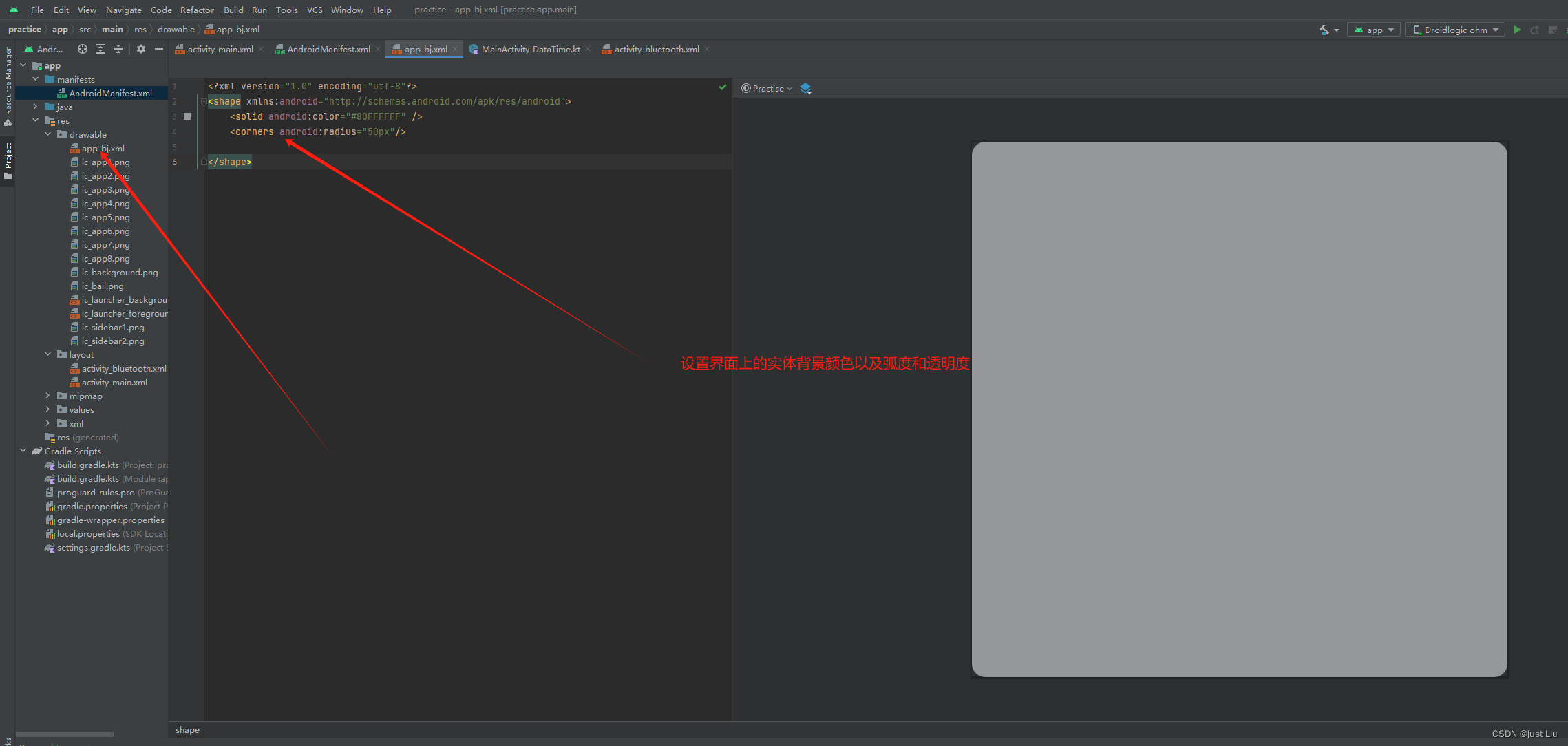
Android studio矩形背景颜色以及弧度的设置
在这里插入图片描述 Android的shape中主要设置的属性 corners:用于设置形状的圆角,可以设置圆角的半径、颜色等属性。 stroke:用于设置形状的边框,可以设置边框的宽度、颜色等属性。 padding:用于设置形状的内边距&…...
Acrel-1000DP分布式光伏系统在某重工企业18MW分布式光伏中应用——安科瑞 顾烊宇
摘 要:分布式光伏发电特指在用户场地附近建设,运行方式以用户侧自发自用、余电上网,且在配电系统平衡调节为特征的光伏发电设施,是一种新型的、具有广阔发展前景的发电和能源综合利用方式,它倡导就近发电,就…...
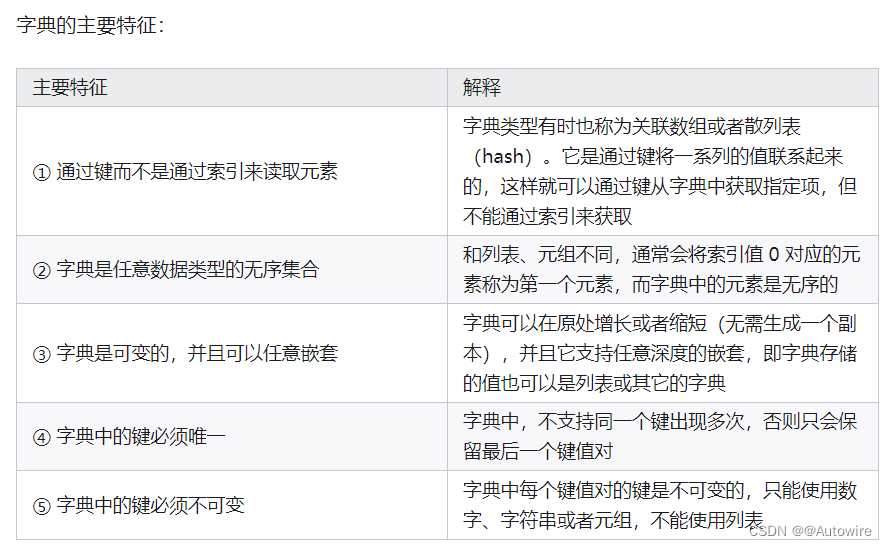
3 python基本语法 - Dict 字典
Python 中字典(dict)是一种无序的、可变的序列,它的元素以“键值对(key-value)”的形式存储。相对地,列表(list)和元组(tuple)都是有序的序列,它们…...

Magnific AI:彻底改变 AI 生成图像的升级
在我最近与 Magnific AI 的讨论中,我不仅感到惊讶,而且对该工具提供的质量和可能性着迷。我发现 Magnific AI 能够转换人工智能生成的图像(这些图像通常只能以低分辨率提供),尤其令人印象深刻,不仅在可打印…...

BKP 备份寄存器 RTC 实时时钟-stm32入门
这一章节我们要讲的主要内容是 RTC 实时时钟,对应手册,是第 16 章的位置。 实时时钟这个东西,本质上是一个定时器,但是这个定时器,是专门用来产生年月日时分秒,这种日期和时间信息的。所以学会了 STM32 的…...

1.1 数据结构-数据的表示
文章目录 1.1.1 二元关系及其性质:1.1.1.1 笛卡尔积:1.1.1.2 二元关系:持续更新当中 ....... 1.1.1 二元关系及其性质: 数据的基本单元称为额数据元素,数据是从客观事物的观测中的到的,数据元素并不是鼓励存在的,而是存在密切的联系,也因此才能表示和描述客观事物,数据元素之间…...
])
UNIX Linux系统 启动PPOCRLabel报错[已放弃 (核心已转储)]
参照官方教程安装后,启动PPOCRLabel报错:[已放弃 (核心已转储)] 官方链接地址:PPOCRLabelv2 $~ PPOCRLabel --lang ch QObject::moveToThread: Current thread (0x561534309430) is not the objects thread (0x56153929eac0). Cannot move to…...

前端开发中的webpack打包工具
前端技术发展迅猛,各种可以提高开发效率的新思想和框架层出不穷,但是它们都有一个共同点,即源代码无法直接运行,必须通过转换后才可以正常运行。webpack是目前主流的打包模块化JavaScript的工具之一。 本章主要涉及的知识点有&am…...
)
Mybatis配置-数据库厂商标识(databaseIdProvider)
MyBatis可以根据数据库供应商执行不同的语句。多数据库供应商支持是基于映射语句的databaseId属性。MyBatis将加载所有没有databaseId属性或具有与当前数据库匹配的databaseId属性的语句。如果找到具有和不具有databaseId的相同语句,则后者将被丢弃。要启用多供应商…...

【Java】使用递归的方法获取层级关系数据demo
使用递归来完善各种业务数据的层级关系的获取 引言:在Java开发中,我们通常会遇到层层递进的关系型数据的获取问题,有时是树状解构,或金字塔结构,怎么描述都行,错综复杂的关系在程序中还是可以理清的。 这…...
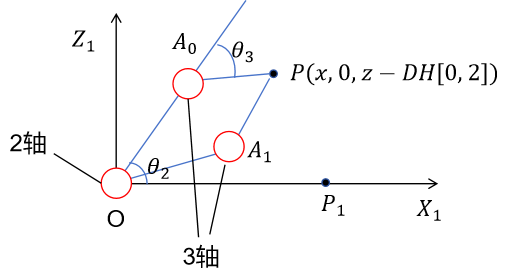
工业6轴机械臂运动学逆解(解析解)
工业6轴机械臂运动学逆解(解析解) 通常工业机械臂采用6旋转轴串连的形式,保证了灵活性,但为其运动学逆解(即已知机械臂末端的位姿 P P P,求机械臂各个旋转轴的旋转角)带来了较大的困难ÿ…...

管理类联考——数学——真题篇——按题型分类——充分性判断题——蒙猜A/B
老规矩,看目录,平均3-5题 文章目录 A/B2023真题(2023-19)-A-选项特点:两个等号;-判断需联立的难易:难,看着感觉需要联立,所以判断联立需要有理论支撑,不然还…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...
