算法设计与分析2023秋-头歌实验-实验七 动态规划
文章目录
- 第1关:数塔问题
- 任务描述
- 相关知识
- 编程要求
- 解题思路
- 测试说明
- 参考答案
- 第2关:最长公共子序列
- 任务描述
- 相关知识
- 编程要求
- 解题思路:
- 测试说明
- 参考答案
- 第3关:求序列-2 11 -4 13 -5 -2的最大子段和
- 任务描述
- 相关知识
- 编程要求
- 解题思路:
- 测试说明
- 参考答案
- 第4关:求最长的单调递增子序列长度
- 任务描述
- 相关知识
- 编程要求
- 解题思路:
- 测试说明
- 参考答案
- 第5关:矩阵连乘问题
- 任务描述
- 相关知识
- 编程要求
- 测试说明
- 参考答案
第1关:数塔问题
任务描述
本关任务:编写用动态规划解决数塔问题。
相关知识
为了完成本关任务,你需要掌握:动态规划。
编程要求
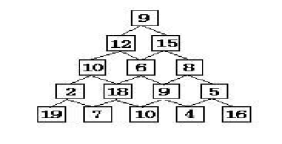
求上图从顶层到顶层的一个路径,使路径上的数字和最大。要求输出最大的数字和max和数值和最大的路径。
解题思路
原始信息有层数和数塔中的数据,层数用一个整型变量n存储,数塔中的数据用二维数组data,存储成如下的下三角阵:
912 1510 6 82 18 9 519 7 10 4 16
必需用二维数组d存储各阶段的决策结果。二维数组d的存储内容如下:、
d[n][j]=data[n][j], j=1,2,……,n;d[i][j]=max(d[i+1][j],d[i+1][j+1])+data[i][j], i=n-1,n-2,……1,j=1,2,……,i
最后d[1][1]存储的就是问题的结果。
测试说明
平台会对你编写的代码进行测试:
测试输入:
5
9
12 15
10 6 8
2 18 9 5
19 7 10 4 16
输出示例:
max=59
数值和最大的路径是:9->12->10->18->10
参考答案
#include <stdio.h>
#define N 5 //问题规模
int main() {int a[50][50];a[1][1] = 9;a[2][1] = 12, a[2][2] = 15;a[3][1] = 10, a[3][2] = 6, a[3][3] = 8;a[4][1] = 2, a[4][2] = 18, a[4][3] = 9, a[4][4] = 5;a[5][1] = 19, a[5][2] = 7, a[5][3] = 10, a[5][4] = 4, a[5][5] = 16;int i, j, dp[50][50] = { 0 }, path[50][50] = { 0 };for (j = 1; j <= N; j++) //初始子问题 ,倒数第二层(第i-1层)开始dp[N][j] = a[N][j];for (i = N - 1; i >= 1; i--) //进行第 i+1 层的决策,从i 到 1 向上for (j = 1; j <= i+1; j++) { //每一层有 i+1 个if (dp[i + 1][j] > dp[i + 1][j + 1]) {dp[i][j] = a[i][j] + dp[i + 1][j];path[i][j] = j; //本次决策选择下标j的元素}else {dp[i][j] = a[i][j] + dp[i + 1][j + 1];path[i][j] = j + 1; //本次决策选择下标j+1的元素}}printf("max=%d\n", dp[1][1]);printf("数值和最大的路径是:"); j = path[1][1]; //计算dp[1][1]的选择for (i = 1; i < N; i++){printf("%d->", a[i][j]);j = path[i][j]; //计算dp[i][j]的选择}printf("%d\n", a[i][j]);}
/********** End **********/
第2关:最长公共子序列
任务描述
本关任务:编写用动态规划解决最长公共子序列问题。
相关知识
为了完成本关任务,你需要掌握:动态规划。
编程要求
求字符串序列“ABCDBAB”和“BDCABA”的最长公共子序列
解题思路:
递推关系分析: 设 A=“a0,a1,…,am−1”,B=“b0,b1,…,bn−1”,Z=“z0,z1,…,zk−1” 为它们的最长公共子序列。 有以下结论: 1)如果am−1=bn−1,则zk−1=am−1=bn−1,且“z0,z1,…,zk−2”是“a0,a1,…,am−2”和“b0,b1,…,bn−2”的一个最长公共子序列; 2)如果am−1=bn−1,则若zk−1=am−1,蕴涵“z0,z1,…,zk−1”是“a0,a1,…,am−2”和“b0,b1,…,bn−1”的一个最长公共子序列; 3)如果am−1=bn−1,则若zk−1=bn−1,蕴涵“z0,z1,…,zk−1”是“a0,a1,…,am−1”和“b0,b1,…,bn−2”的一个最长公共子序列。 定义c[i][j]为序列“a0,a1,…,ai−1”和“b0,b1,…,bj−1”的最长公共子序列的长度,计算c[i][j]可递归地表述如下: 1)c[i][j]=0 如果i=0或j=0; 2)c[i][j]=c[i−1][j−1]+1 如果i,j>0,且a[i−1]=b[j−1]; 3)c[i][j]=max(c[i][j−1],c[i−1][j]) 如果i,j>0,且a[i−1]=b[j−1]。 由二维数组c的递归定义,c[i][j]的结果依赖于c[i−1][j−1],c[i−1][j]和c[i][j−1]。可以从c[m][n]开始,跟踪c[i][j]结果的产生过程,从而逆向构造出最长公共子序列。
测试说明
平台会对你编写的代码进行测试:
测试输入:
a=“ABCDBAB”
b=“BDCABA”
输出示例:
BCBA
参考答案
/*动态规划之最大子序列*/
#include <stdio.h>
int main()
{char A[7]={'A','B','C','B','D','A','B'}; char B[6]={'B','D','C','A','B','A'};int dp[8][7]; //dp数组记录最长公共子序列的长度 for(int i=0;i<7;i++) //边界赋值为0 {dp[i][0]=0;}for(int i=0;i<8;i++){dp[0][i]=0;}// printf("test1=%d\n",dp[6][7]);for(int i=1;i<=7;i++){for(int j=1;j<=6;j++){if(A[i-1]==B[j-1]) //如果相等就dp[i][j]=dp[i-1][j-1]+1; {dp[i][j]=dp[i-1][j-1]+1;}else{if(dp[i-1][j]>dp[i][j-1]){dp[i][j]=dp[i-1][j]; //取两者之间较大者;局部的最优值 }else{dp[i][j]=dp[i][j-1];} }}}char str[100]; //记录公共的字符int i=7,j=6;int count=0;while(i>0&&j>0){if(dp[i][j]==dp[i-1][j]) //往上遍历 {i--;}else if(dp[i][j]==dp[i][j-1]) //往左遍历 {j--;}else{str[count++]=A[i-1];i--;j--;}}for(int i=count-1;i>=0;i--){printf("%c",str[i]);} }
第3关:求序列-2 11 -4 13 -5 -2的最大子段和
任务描述
本关任务:编写用动态规划解决最大子段和问题。
相关知识
为了完成本关任务,你需要掌握:动态规划。
编程要求
给定由n个整数(可能为负数)组成的序列:a1,a2,……,an, 求该序列的最大子段和。当所有整数均为负数,定义其最大子段和为0。
解题思路:
定义b[j]=max(a[i]+a[i+1]+…+a[j]),其中1<=i<=j,并且1<=j<=n。那么所求的最大子段和可以表示为max b[j],1<=j<=n。 由b[j]的定义可知,当b[j−1]>0时b[j]=b[j−1]+a[j],否则b[j]=a[j]。故b[j]的动态规划递归表达式为: b[j]=max(b[j−1]+a[j],a[j]),1<=j<=n。
测试说明
平台会对你编写的代码进行测试:
测试输入:
6
-2 11 -4 13 -5 -2
输出示例:
20
参考答案
#include <stdio.h>
/********** Begin **********/
int main(){int n;scanf("%d",&n);int a[n][2];int max=0;for(int i=0;i<n;i++){scanf("%d",&a[i][0]);if(i==0){a[i][1]=a[i][0];}else{a[i][1]=a[i-1][1]+a[i][0]>a[i][0]?a[i-1][1]+a[i][0]:a[i][0];}max=max>a[i][1]?max:a[i][1];}printf("%d",max);return 0;}
/********** End **********/
第4关:求最长的单调递增子序列长度
任务描述
本关任务:编写用动态规划解决求最长的单调递增子序列长度问题。
相关知识
为了完成本关任务,你需要掌握:动态规划。
编程要求
给定一个长度为n的数组,找出一个最长的单调递增子序列(不一定连续,但是顺序不能乱)。例如:给定一个长度为7的数组A5,6,7,1,2,8,9,则其最长的单调递增子序列为5,6,7,8,9,长度为5。求318714101223411624的最长的单调递增子序列长度。
解题思路:
设长度为n的数组为(a[0],a[1],a[2],…,a[n−1]),则假定以a[j]结尾的数组序列的最长递增子序列长度为L(j),则L(j)=max(L(i))+1,i<j且a[i]<a[j]。也就是说,我们需要遍历在j之前的所有位置i(从0到j−1),找出满足条件a[i]<a[j]的L(i),求出max(L(i))+1即为L(j)的值。最后,我们遍历所有的L(j)(从0到n−1),找出最大值即为最大递增子序列。
测试说明
平台会对你编写的代码进行测试:
测试输入:
10
3 18 7 14 10 12 23 41 16 24
输出示例:
6
参考答案
#include <stdio.h>
/********** Begin **********/
int main(){int n;scanf("%d",&n);int m[n][3];m[0][1]=1;m[0][2]=0;for(int i=0;i<n;i++){scanf("%d",&m[i][0]);if(i!=0){m[i][1]=0;int k=i-1;while(k>=0){if(m[i][0]>m[k][0]){if(k==i-1){m[i][1]=m[k][1]+1;m[i][2]=k;}else{int max=m[k][1]+1;if(max>m[i][1]){m[i][1]=max;m[i][2]=k; }}}k--;}if(k<0&&m[i][1]==0){m[i][1]=1;m[i][2]=i;}}}int max=m[0][1],j=0;for(int i=0;i<n;i++){if(m[i][1]>=max){max=m[i][1];j=i;}}printf("%d\n",max);
}
/********** End **********/
第5关:矩阵连乘问题
任务描述
本关任务:编写用动态规划解决矩阵连乘问题。
相关知识
为了完成本关任务,你需要掌握:动态规划。
编程要求
将矩阵连乘积AiAi+1…Aj简记为A[i:j],其中i<=j。设在矩阵Ak和Ak+1之间将矩阵链断开,则其相应加括号为(AiAi+1…Ak) (Ak+1Ak+2…Aj)。A[i:j]的计算量等于三部分计算量之和: (1)A[i:k]的计算量, (2)A[k+1:j]的计算量, (3)A[i:k]与A[k+1:j]相乘的计算量。 设计算A[i:j]所需最少乘积数目为,则原问题的最优值为。 当i=j时,a[i:j]=Ai,因此,m[i][j]=0,i=1,⋅⋅⋅,n 当i<j时,m[i][j]=i<k<jmin{m[i][k]+m[k+1][j]+pi−1pkpj} 其中,矩阵Ai的矩阵数为pi−1×pi 矩阵A1的维度:p0p1=3035 矩阵A2的维度:p1p2=3515 矩阵A3的维度:p2p3=155 矩阵A4的维度:p3p4=510 矩阵A5的维度:p4p5=1020 矩阵A6的维度:p5p6=2025 求这6个矩阵连乘的最小相乘次数。
测试说明
平台会对你编写的代码进行测试:
测试输入:
6
30 35
35 15
15 5
5 10
10 20
20 25
输出示例:
m[1][6]=15125
参考答案
#include <stdio.h>
#include <stdlib.h>
/********** Begin **********/
int main(){int n;scanf("%d",&n);int a[n][2];int b[n][n]={0};for(int i=0;i<n;i++){scanf("%d %d",&a[i][0],&a[i][1]); }for(int i=1;i<n;i++){for(int j=0;j<n-i;j++){b[j][j+i]=b[j][j]+b[j+1][j+i]+a[j][0]*a[j][1]*a[j+i][1]; int k=j+1;for(;k<j+i;k++){int t=b[j][k]+b[k+1][j+i]+a[j][0]*a[k][1]*a[j+i][1];if(t<b[j][j+i]) {b[j][j+i]=t;}}}}printf("m[%d][%d]=%d",1,n,b[0][n-1]);return 0;
}
/********** End **********/
相关文章:

算法设计与分析2023秋-头歌实验-实验七 动态规划
文章目录 第1关:数塔问题任务描述相关知识编程要求解题思路测试说明参考答案 第2关:最长公共子序列任务描述相关知识编程要求解题思路:测试说明参考答案 第3关:求序列-2 11 -4 13 -5 -2的最大子段和任务描述相关知识编程要求解题思…...

复杂 SQL 实现分组分情况分页查询
其他系列文章导航 Java基础合集数据结构与算法合集 设计模式合集 多线程合集 分布式合集 ES合集 文章目录 其他系列文章导航 文章目录 前言 一、根据 camp_status 字段分为 6 种情况 1.1 SQL语句 1.2 SQL解释 二、分页 SQL 实现 2.1 SQL语句 2.2 根据 camp_type 区分返…...

JavaScript---如何完美的判断返回对象是否有值
如何判断一个对象为空是我们在开发中经常会遇到的问题,今天我们来聊聊几种经常使用的方法,以及在不同的场景下我们如何去使用。 1. JSON.stringify JSON.stringify 方法可以使对象序列化,转为相应的 JSON 格式。 js 复制代码 const obj {…...
kafka offset sasl加密连接
kafka-tool(offset) 进行SCRAM连接,直接上图 填写jaas的认证(账密 引用包)...
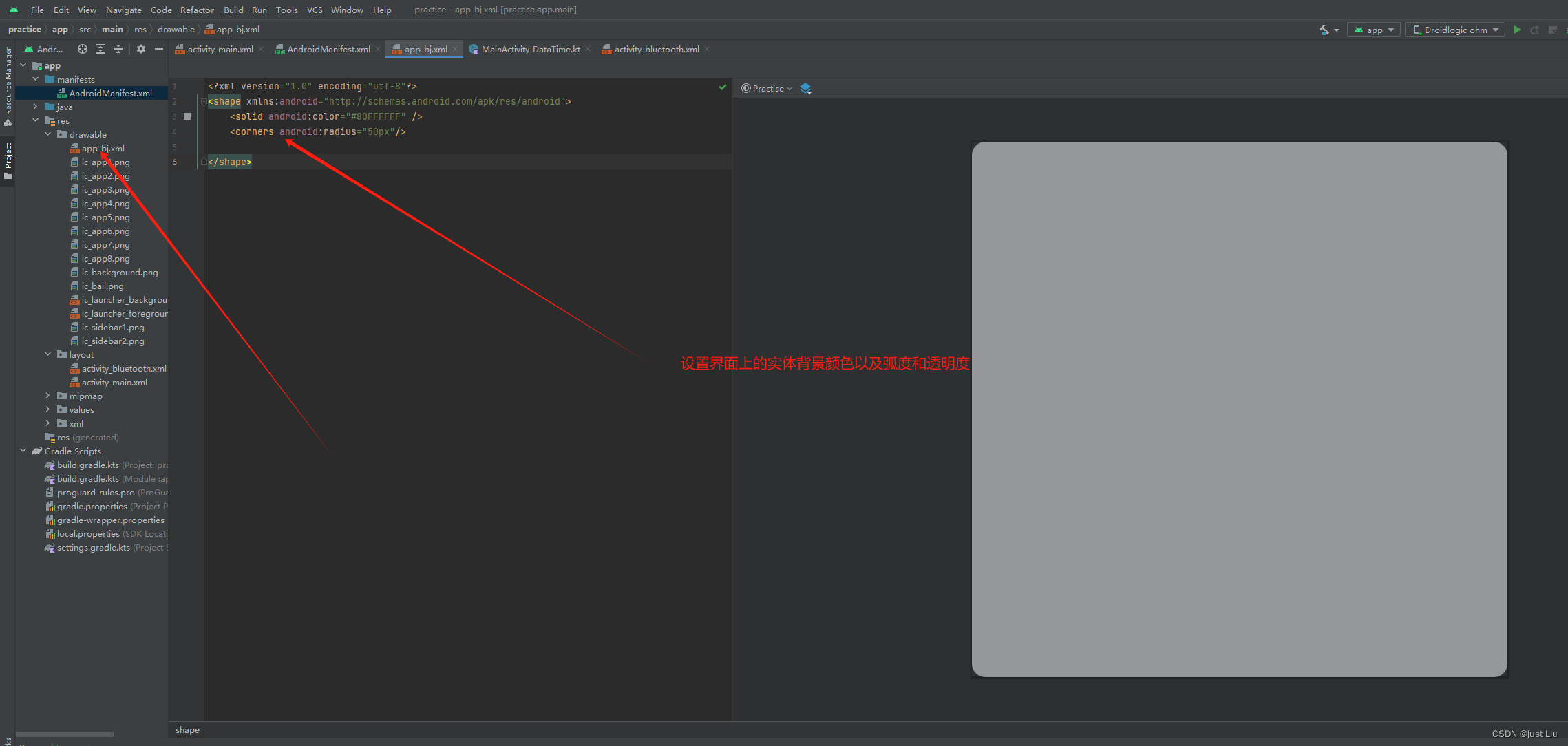
Android studio矩形背景颜色以及弧度的设置
在这里插入图片描述 Android的shape中主要设置的属性 corners:用于设置形状的圆角,可以设置圆角的半径、颜色等属性。 stroke:用于设置形状的边框,可以设置边框的宽度、颜色等属性。 padding:用于设置形状的内边距&…...
Acrel-1000DP分布式光伏系统在某重工企业18MW分布式光伏中应用——安科瑞 顾烊宇
摘 要:分布式光伏发电特指在用户场地附近建设,运行方式以用户侧自发自用、余电上网,且在配电系统平衡调节为特征的光伏发电设施,是一种新型的、具有广阔发展前景的发电和能源综合利用方式,它倡导就近发电,就…...
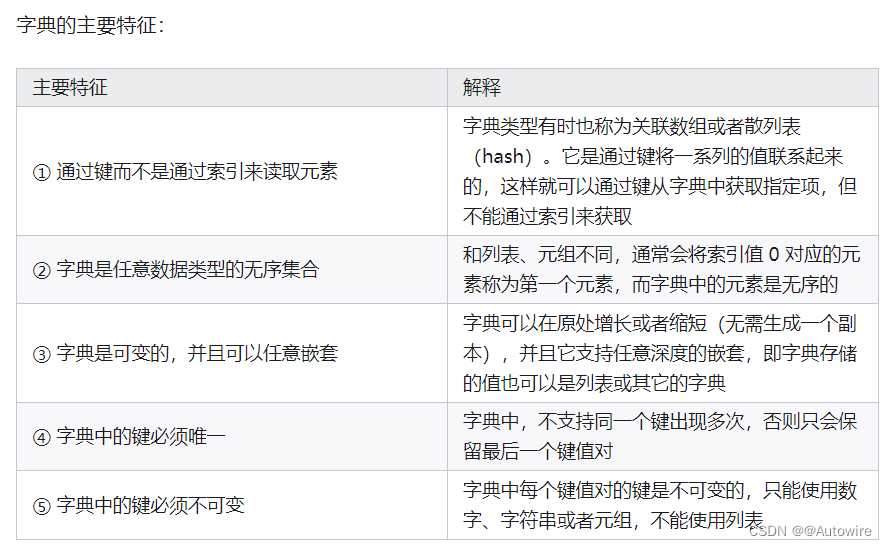
3 python基本语法 - Dict 字典
Python 中字典(dict)是一种无序的、可变的序列,它的元素以“键值对(key-value)”的形式存储。相对地,列表(list)和元组(tuple)都是有序的序列,它们…...

Magnific AI:彻底改变 AI 生成图像的升级
在我最近与 Magnific AI 的讨论中,我不仅感到惊讶,而且对该工具提供的质量和可能性着迷。我发现 Magnific AI 能够转换人工智能生成的图像(这些图像通常只能以低分辨率提供),尤其令人印象深刻,不仅在可打印…...

BKP 备份寄存器 RTC 实时时钟-stm32入门
这一章节我们要讲的主要内容是 RTC 实时时钟,对应手册,是第 16 章的位置。 实时时钟这个东西,本质上是一个定时器,但是这个定时器,是专门用来产生年月日时分秒,这种日期和时间信息的。所以学会了 STM32 的…...

1.1 数据结构-数据的表示
文章目录 1.1.1 二元关系及其性质:1.1.1.1 笛卡尔积:1.1.1.2 二元关系:持续更新当中 ....... 1.1.1 二元关系及其性质: 数据的基本单元称为额数据元素,数据是从客观事物的观测中的到的,数据元素并不是鼓励存在的,而是存在密切的联系,也因此才能表示和描述客观事物,数据元素之间…...
])
UNIX Linux系统 启动PPOCRLabel报错[已放弃 (核心已转储)]
参照官方教程安装后,启动PPOCRLabel报错:[已放弃 (核心已转储)] 官方链接地址:PPOCRLabelv2 $~ PPOCRLabel --lang ch QObject::moveToThread: Current thread (0x561534309430) is not the objects thread (0x56153929eac0). Cannot move to…...

前端开发中的webpack打包工具
前端技术发展迅猛,各种可以提高开发效率的新思想和框架层出不穷,但是它们都有一个共同点,即源代码无法直接运行,必须通过转换后才可以正常运行。webpack是目前主流的打包模块化JavaScript的工具之一。 本章主要涉及的知识点有&am…...
)
Mybatis配置-数据库厂商标识(databaseIdProvider)
MyBatis可以根据数据库供应商执行不同的语句。多数据库供应商支持是基于映射语句的databaseId属性。MyBatis将加载所有没有databaseId属性或具有与当前数据库匹配的databaseId属性的语句。如果找到具有和不具有databaseId的相同语句,则后者将被丢弃。要启用多供应商…...

【Java】使用递归的方法获取层级关系数据demo
使用递归来完善各种业务数据的层级关系的获取 引言:在Java开发中,我们通常会遇到层层递进的关系型数据的获取问题,有时是树状解构,或金字塔结构,怎么描述都行,错综复杂的关系在程序中还是可以理清的。 这…...
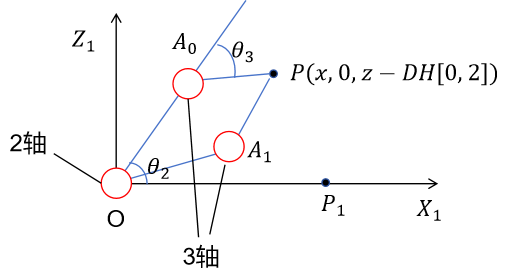
工业6轴机械臂运动学逆解(解析解)
工业6轴机械臂运动学逆解(解析解) 通常工业机械臂采用6旋转轴串连的形式,保证了灵活性,但为其运动学逆解(即已知机械臂末端的位姿 P P P,求机械臂各个旋转轴的旋转角)带来了较大的困难ÿ…...

管理类联考——数学——真题篇——按题型分类——充分性判断题——蒙猜A/B
老规矩,看目录,平均3-5题 文章目录 A/B2023真题(2023-19)-A-选项特点:两个等号;-判断需联立的难易:难,看着感觉需要联立,所以判断联立需要有理论支撑,不然还…...
为什么GRU和LSTM能够缓解梯度消失或梯度爆炸问题?
1、什么是梯度消失(gradient vanishing)? 参数更新过小,在每次更新时几乎不会移动,导致模型无法学习。 2、什么是梯度爆炸(gradient exploding)? 参数更新过小大,破坏了…...

【力扣100】146.LRU缓存
添加链接描述 class DLinkedNode:def __init__(self, key0, value0):self.key keyself.value valueself.prev Noneself.next Noneclass LRUCache:def __init__(self, capacity: int):self.cache dict()# 使用伪头部和伪尾部节点 self.head DLinkedNode()self.tail D…...
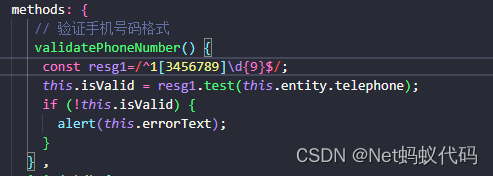
【Vue中给输入框加入js验证_blur失去焦点进行校验】
【Vue中给输入框加入js验证_blur失去焦点进行校验】 通俗一点就是给输入框加个光标离开当前文本输入框时,然后对当前文本框内容进行校验判断 具体如下: 1.先给文本框加属性 blur“validatePhoneNumber” <el-input v-model“entity.telephone” blur…...

vue3项目引入电子签名(可横屏竖屏)
实现效果:(左边横屏,右边竖屏) 前言:【使用开源项目smooth-signature 实现签名的功能。Gitee 地址是 :GitHub - linjc/smooth-signature: H5带笔锋手写签名,支持PC端和移动端,任何前…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...
