堆与二叉树(上)
本篇主要讲的是一些概念,推论和堆的实现(核心在堆的实现这一块)
涉及到的一些结论,证明放到最后,可以选择跳过,知识点过多,当复习一用差不多,如果是刚学这一块的,建议打勾的概念多留意,推论前三个相似,了解其中一个即可,重点看推论四(主要是和堆的实现有关),一定要动手实现堆排序哦,希望对你们有帮助
讲堆之前我们先介绍一下 树 的概念
一 . 树的概念
什么是树?
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。它的结构很像一棵倒过来的树

正因为这一点,有些结构的名称就可以跟数联系起来
- 其中一个特殊的节点叫作根节点,它没有前驱结点
- 除根节点以外,其余若干个集合叫作子树(子树之间不能相交)
- 除根节点以外,每个父节点都有一个前驱结点
错误的图示
树的相关知识
图例:
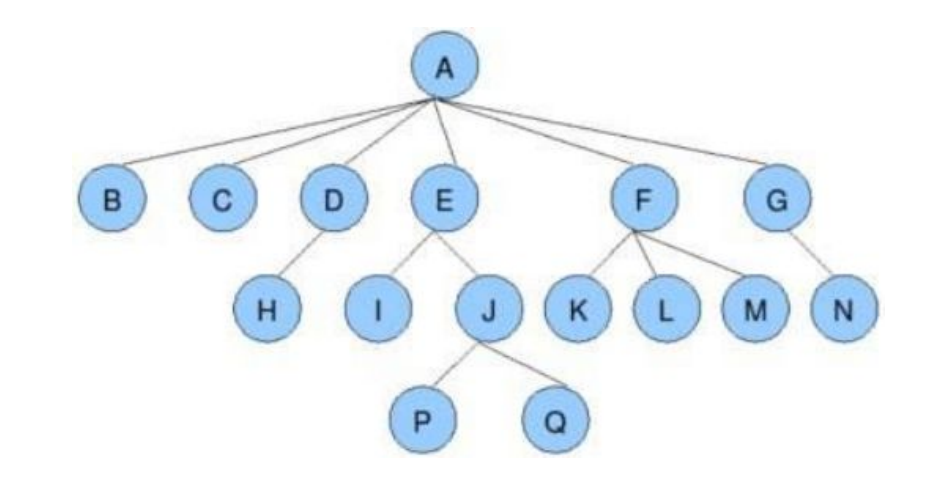
✔节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点
✔双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点 (注:A不仅是根节点,也是父节点)
✔孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推
✔树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林;
二. 二叉树
二叉树的概念
二叉树是一种特殊的树
每个父节点都最多有两个子节点
图例1

特殊的二叉树
- 满二叉树
要求每一个父节点必须有两个子节点(如上述图例1)
2. 完全二叉树
要求节点是连续存放的
(这里用数组的存储形式来说明)
正确示范:

错误示范:

二叉树的一些推论
规定根节点的层数为 1 ,总层数为 h ,节点个数为 n
推论1
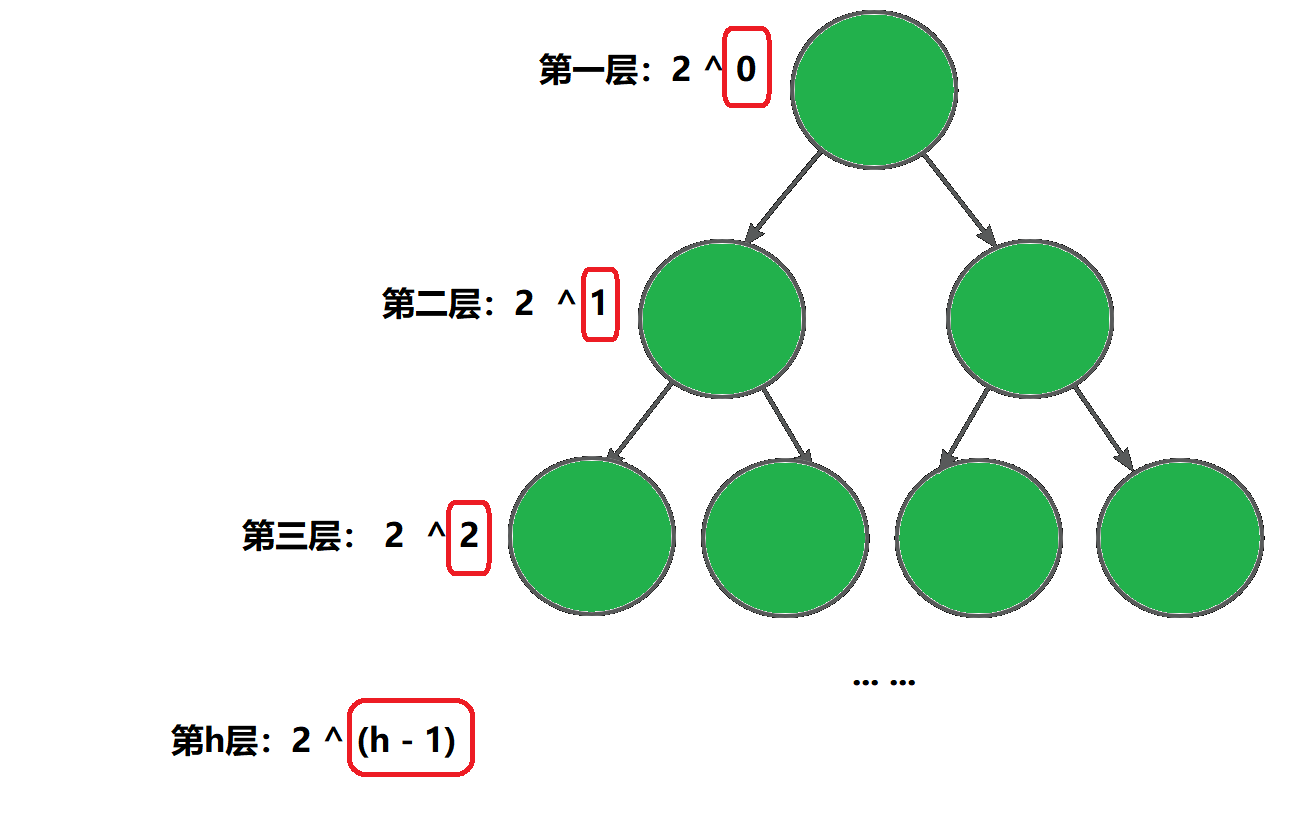
已知总层数为 h,求最后一层的节点个数的最大值:
2 ^(h - 1)
推论2
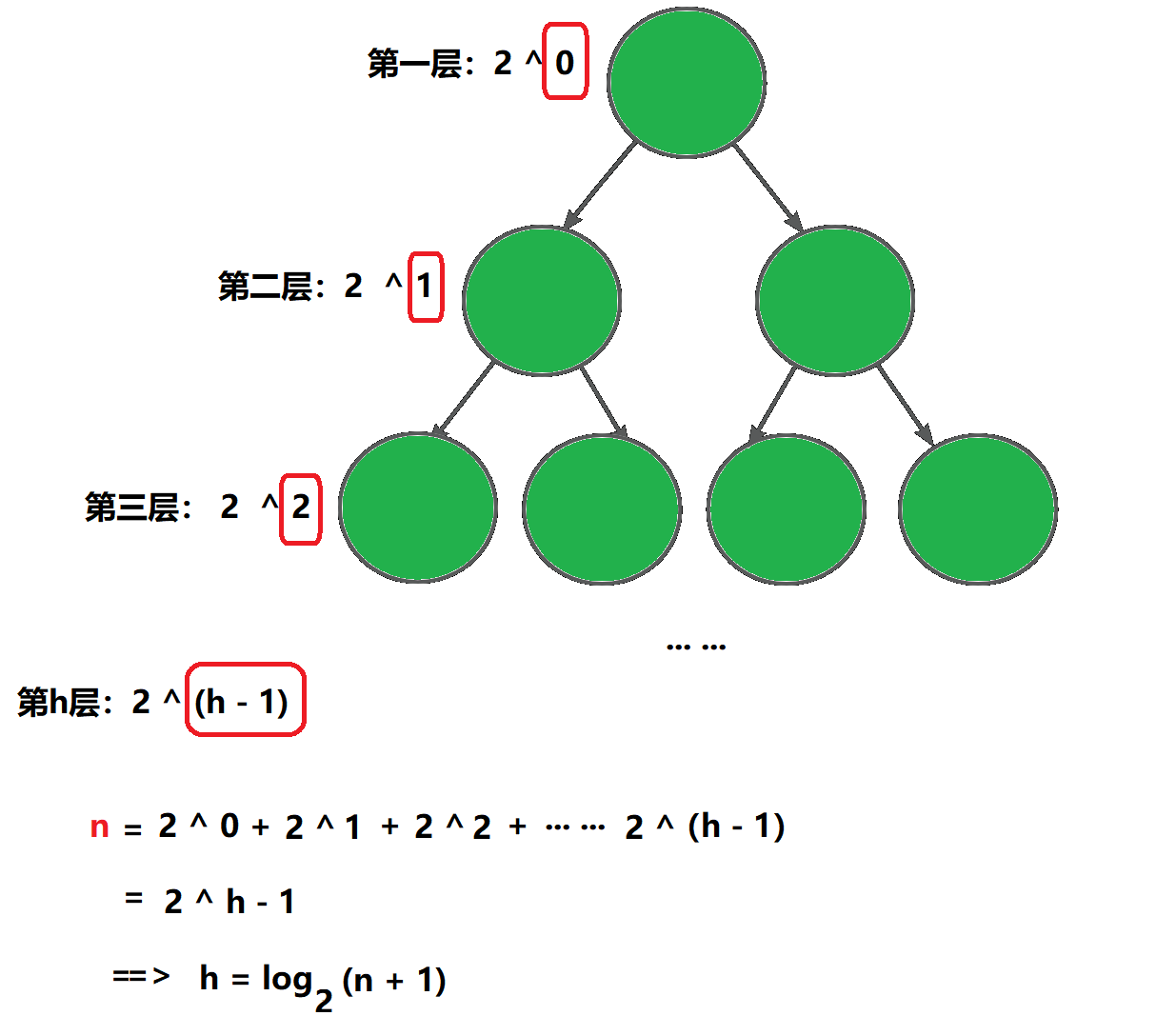
已知节点个数为 n,求具有n个结点的满二叉树的深度 h
推论3
若根节点层数为1(保证不是空树),已知深度为 h ,则求二叉树的最大节点数:
推论4
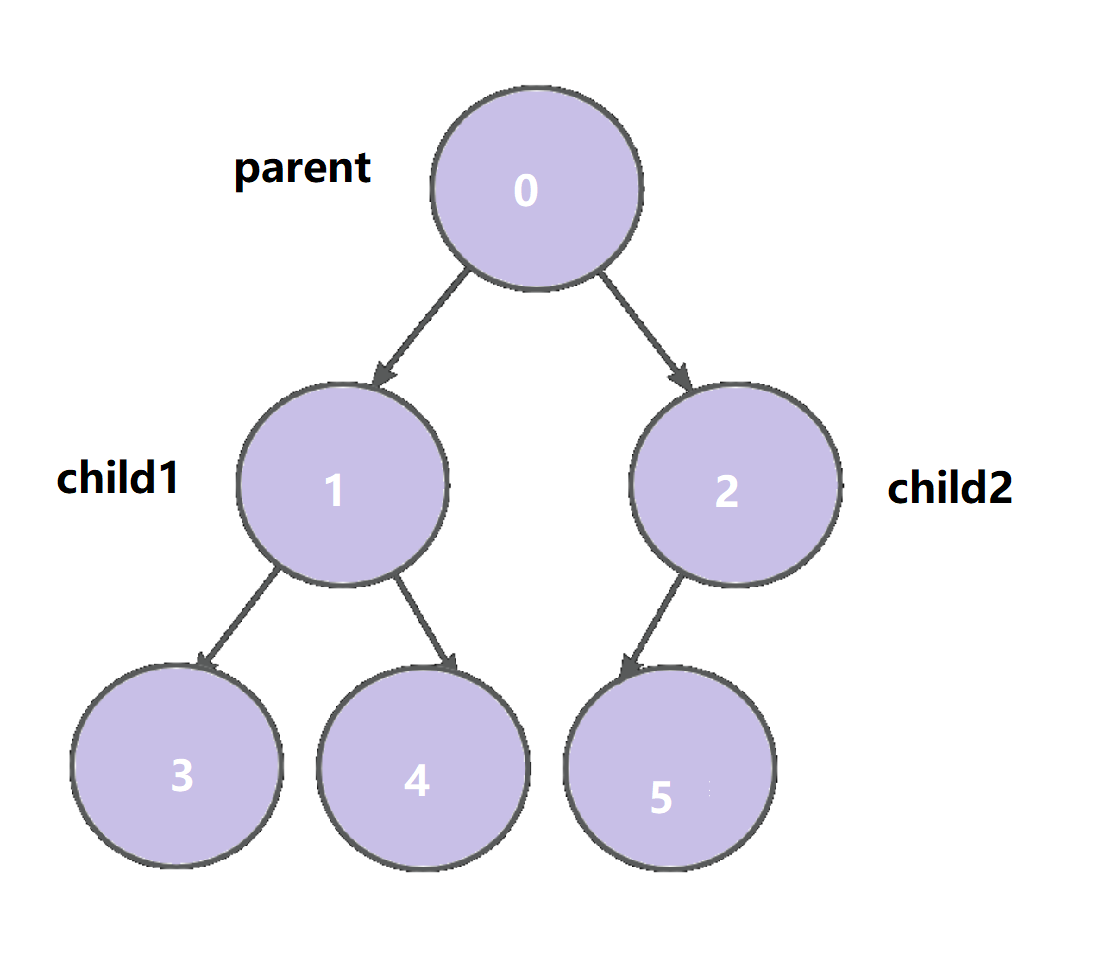
已经节点总个数 n 的完全二叉树 ,从第一个根节点开始以 0 编号,从左到右,从上到下编号依次增加 1
求 父节点 和 左右孩子节点 的关系(parent , child 1 和 child2 都是下标)
a. 若知道 parent:
则 child1 = parent * 2 + 1
child2 = parent * 2 + 2
b. 若知道 child (无论哪个孩子下标都可以):
则 parent = (child - 1) / 2
推论5
对任何一棵二叉树, 如果度为0其叶结点个数为 n0 , 度为2的分支结点个数为 n2 ,
则有 n0 = n2 +1
证明推论5
用图例阐明遇到的情况:

我们发现当 n1 + 1 ,意味着 n0 - 1
n2 + 1 , 意味着 n1 - 1
证明推论1
证明推论2
证明推论3
是推论2
(即是满二叉树)
证明推论4
完全二叉树有一个性质,它是连续存放的
第一个结论通过画图我们很容易就得到了
第二个结论主要注意的是:
由于下标都是 int 类型的,最终得到的一定是整数
证明推论5
用图例阐明遇到的情况:
我们发现当 n1 + 1 ,意味着 n0 - 1
n2 + 1 , 意味着 n1 - 1
三 . 二叉树的储存结构
二叉树有两种储存形式:
一个是 顺序储存结构 , 另一个是 链式储存结构
- 顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树就会有空间的浪费
图例
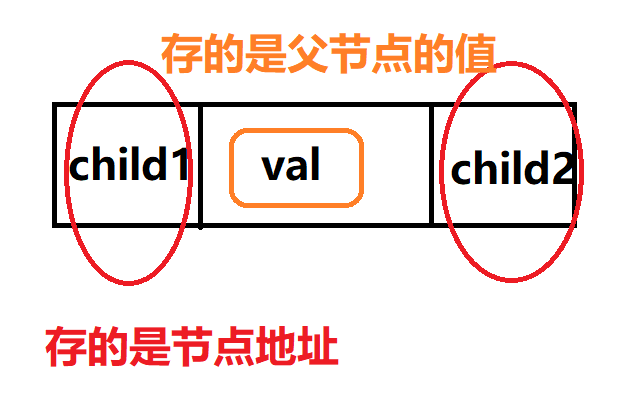
2. 二叉树的链式存储结构是指,用链表来表示一棵二叉树,
一般两个指针存放左右孩子的节点
图例
四 . 堆的概念
堆的性质
堆满足以下性质:
- 是一棵 完全二叉树
- 只有 小堆 或者 大堆
(小堆:父节点的值永远小于等于两个孩子节点的值;
大堆:父节点的值永远大于等于两个孩子节点的值)
图例
堆的实现
1. 堆的排序
堆的排序有两种:向上排序法 和 向下排序法(这里用顺序结构)
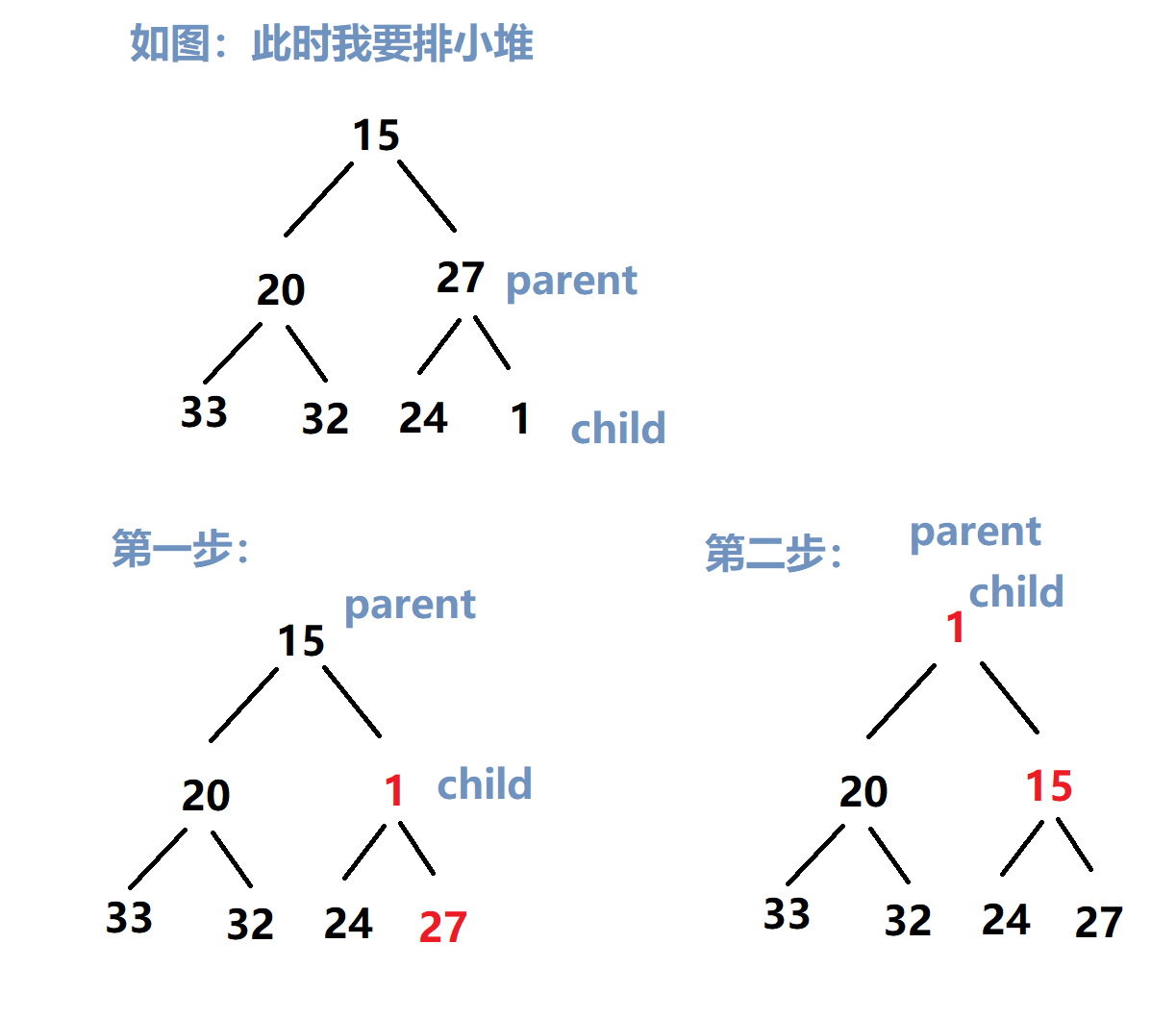
向上排序法
该方法可以在一个个把数值放进去的同时进行排序
实现思路如下:
父节点下标从 0 开始,一个节点也是一个堆(所以放入第一个数的时候是不用进行排序的),后面的数先把值放入数组,再进行与父节点进行对比(已知 child 下标,求 parent 下标,回到推论4)
[由于可能发生多次交换问题,这里需要用到循环]
如果 父节点 的值 大于 子节点 的值(排小堆),则交换;
如果 父节点 的值 小于 子节点 的值(排大堆),则交换.
并且 此时 child 下标 和 parent 下标都要发生改变,让上一个父节点和上一个子节点作比较
注意:想要改变两个值,一定要传地址
结束条件:
如果不用交换可以跳出循环
或者到 child > 0 时,跳出循环
代码
void swap(int* p1, int* p2)
{if (*p1 == *p2){return;}else{int tmp = *p1;*p1 = *p2;*p2 = tmp;}
}
void upAdjust(int* pa, int n)
{for (int i = 1; i < n; i++){int child = i;int parent = (child - 1) / 2;while (child > 0){if (pa[parent] > pa[child]){swap(&pa[parent], &pa[child]);child = parent;parent = (child - 1) / 2;}else{break;}}}}向下排序法
给一组无序数组,我们给它排序,这里需要我们从最后一棵子树(度不为0)的父节点和它的子节点开始倒着排序
像这样:
我们以第一棵树为例(序号为1的树)
这里更容易找到子节点 , 然后根据公式推出父节点
但是我们的思路是 让父节点与 (更小的)子节点比较(小堆),或者与(更大的)子节点比较 (大堆)
这里的子节点需要通过比较确定,所以我们先去找父节点的下标起
parent = (n - 1) / 2
child = parent * 2 + 1(假设第一个节点就是我们需要比较的那个节点)
再与第二个节点进行对比,确定 child 下标(判断时为了防止没有第二个子节点而越界的情况,一定要对其进行判断)
对比 父节点 和 子节点 的值
我们还需要向下调整
此时 parent = child
child = parent * 2 + 1
一直到 child >= n (这是最内层的循环结束条件)
比完第一棵树,再比第二棵树
此时 parent -= 1 (完全二叉树是连续的)
注意:由于可能发生连续向下的调整,导致 parent 的值会发生改变,所以我们需要得到第一棵树最开始的 parent
child = parent * 2 + 1
重复上述动作,直到
parent >= 0(这是最外层的循环条件)
代码
void swap(int* p1, int* p2)
{if (*p1 == *p2){return;}else{int tmp = *p1;*p1 = *p2;*p2 = tmp;}
}
void downAdjust(int* pa, int parent, int n)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && pa[child] > pa[child + 1]){child++;}if (pa[parent] > pa[child]){swap(&pa[parent], &pa[child]);}parent = child;child = parent * 2 + 1;else{break;}}
}
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{downAdjust(arr,i,n);
}2. 实现堆
堆的实现分几步:(这里用顺序结构)
堆的步骤
a. 构造一个堆的结构体
结构体成员:
存放整型数组的指针 : int *a
整个数组的元素个数 : int size
整个数组的的容量 : int capacity
b. 初始化结构体
size = 0
让 a 动态开辟 4 * sizeof(int) 个字节
capacity = 4
c. 放入元素
创建一个自定义函数放入元素
注意:
若 size ==capacity,开辟 sizeof( int ) * capacity * 2 的字节
capacity = capacity * 2
先一个个从插入元素,再进行调整(这里我们用向上调整法)
size++
d. 判断是否为空
创建一个自定义函数,判断数组里面是否还有元素很简单,只要判断
size == 0 即可
e. 删除元素(这里我们的删除一定是删除根节点的值)
创建一个自定义函数删除元素
删除元素第一步是一定要判断是否为空
为了继续维护堆,我们需要一个元素覆盖根节点的值,从而抹去这个值,但是如果根节点与它的子节点直接进行覆盖,会破坏之前的大堆(或 小堆)
所以我们的办法是:
把根节点的值与最后一个值交换(保证其它的父子关系不变)
size--
我们再使用 向下调整法
f. 打印堆
g. 释放堆的空间
代码
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
typedef struct HeapList
{int* a;int size;int capacity;
}HP;
void InitHeap(HP *heap)
{int* pa = (int*)malloc(sizeof(int) * 4);if (pa == NULL){perror("realloc");return;}heap->a = pa;heap->capacity = 4;heap->size = 0;
}
void swap(int* p1, int* p2)
{if (*p1 == *p2){return;}else{int tmp = *p1;*p1 = *p2;*p2 = tmp;}
}
void upAdjust(int* pa, int n)
{for (int i = 1; i < n; i++){int child = i;int parent = (child - 1) / 2;while (child > 0){if (pa[parent] > pa[child]){swap(&pa[parent], &pa[child]);child = parent;parent = (child - 1) / 2;}else{break;}}}}
void downAdjust(int* pa, int parent, int n)
{int child = parent * 2 + 1;while (child < n){if (child + 1 < n && pa[child] > pa[child + 1]){child++;}if (pa[parent] > pa[child]){swap(&pa[parent], &pa[child]);}parent = child;child = parent * 2 + 1;}
}
void HeapPush(HP* heap ,int x)
{if (heap->size == heap->capacity){int* pa = (int*)realloc(heap->a, sizeof(int) * heap->capacity * 2);if (pa == NULL){perror("realloc");return;}heap->a = pa;heap->capacity = heap->capacity * 2;}heap->a[heap->size] = x;heap->size++;upAdjust(heap->a, heap->size);
}
bool IsEmpty(HP* heap)
{return heap->size == 0;
}
void HeapPop(HP* heap)
{assert(!IsEmpty(heap));swap(&heap->a[0], &heap->a[heap->size - 1]);heap->size--;downAdjust(heap->a, 0, heap->size);
}
void PrintHeap(HP* heap)
{for (int i = 0; i < heap->size; i++){printf("%d ", heap->a[i]);}printf("\n");
}
void DestoryHeap(HP* heap)
{free(heap->a);heap->a = NULL;heap->size = heap->capacity = 0;
}相关文章:
堆与二叉树(上)
本篇主要讲的是一些概念,推论和堆的实现(核心在堆的实现这一块) 涉及到的一些结论,证明放到最后,可以选择跳过,知识点过多,当复习一用差不多,如果是刚学这一块的,建议打…...

HBase查询的一些限制与解决方案
Apache HBase 是一个开源的、非关系型、分布式数据库,它是 Hadoop 生态系统的一部分,用于存储和处理大量的稀疏数据。HBase 在设计上是为了提供快速的随机读写能力,但与此同时,它也带来了一些查询上的限制: 没有SQL支持…...

软件开发 VS Web开发
我的新书《Android App开发入门与实战》已于2020年8月由人民邮电出版社出版,欢迎购买。点击进入详情 目录 介绍: 角色和职责: 软件开发人员: Web开发人员: 技能: 软件开发人员: Web开发人…...
基于Springboot的旅游网站设计与实现(论文+调试+源码)
项目描述 临近学期结束,还是毕业设计,你还在做java程序网络编程,期末作业,老师的作业要求觉得大了吗?不知道毕业设计该怎么办?网页功能的数量是否太多?没有合适的类型或系统?等等。这里根据疫情当下,你想解决的问…...
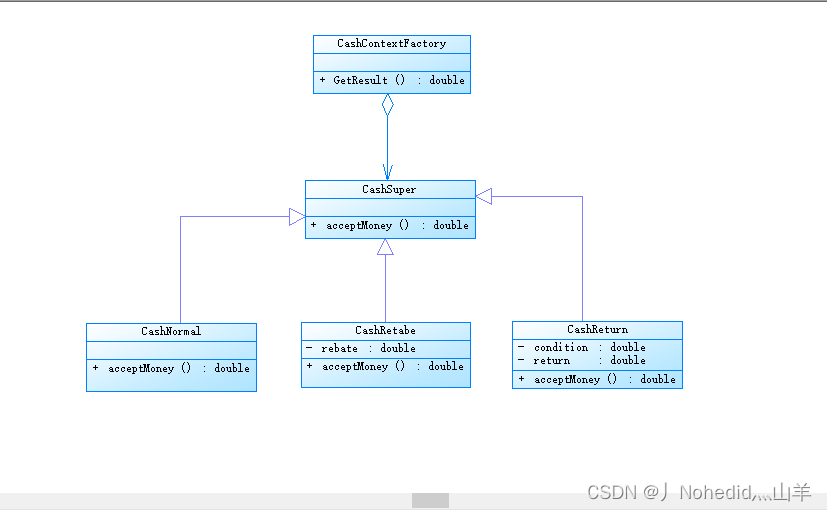
【从零开始学习--设计模式--策略模式】
返回首页 前言 感谢各位同学的关注与支持,我会一直更新此专题,竭尽所能整理出更为详细的内容分享给大家,但碍于时间及精力有限,代码分享较少,后续会把所有代码示例整理到github,敬请期待。 此章节介绍策…...
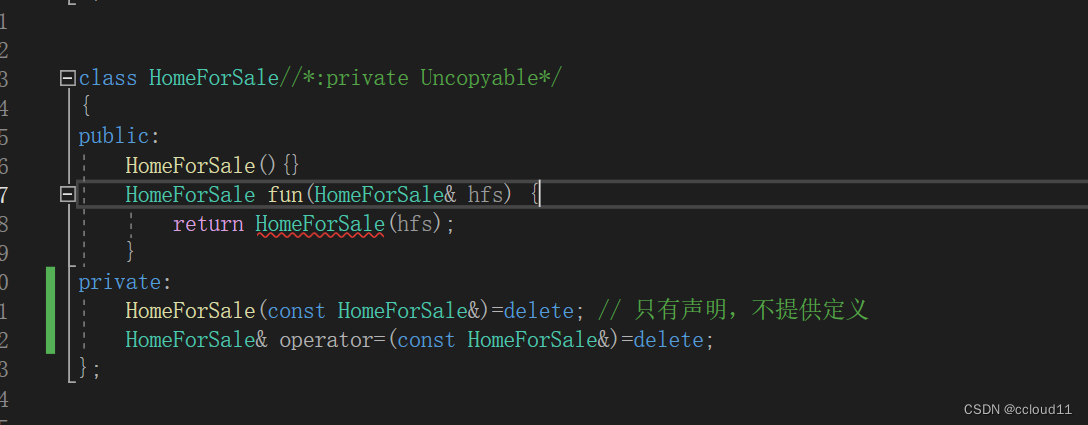
条款6:若不想使用编译器自动生成的函数,就该明确拒绝
有些场景我们不需要编译器默认实现的构造函数,拷贝构造函数,赋值函数,这时候我们应该明确的告诉编译器,我们不需要,一个可行的方法是将拷贝构造函数和赋值函数声明为private。 class HomeForSale { ... }; HomeForSal…...
零基础也能制作家装预约咨询小程序
近年来,随着互联网的快速发展,越来越多的消费者倾向于使用手机进行购物和咨询。然而,许多家装实体店却发现自己的客流量越来越少,急需一种新的方式来吸引顾客。而开发家装预约咨询小程序则成为了一种利用互联网技术来解决这一问题…...

Mybatis的插件运⾏原理,如何编写⼀个插件?
🚀 作者主页: 有来技术 🔥 开源项目: youlai-mall 🍃 vue3-element-admin 🍃 youlai-boot 🌺 仓库主页: Gitee 💫 Github 💫 GitCode 💖 欢迎点赞…...

C++复合数据类型:字符数组|读取键盘输入|简单读写文件
文章目录 字符数组(C风格字符串)读取键盘输入使用输入操作符读取单词读取一行信息getline使用get读取一个字符 读写文件 字符数组(C风格字符串) 字符串就是一串字符的集合,本质上其实是一个“字符的数组”。 在C中为了…...
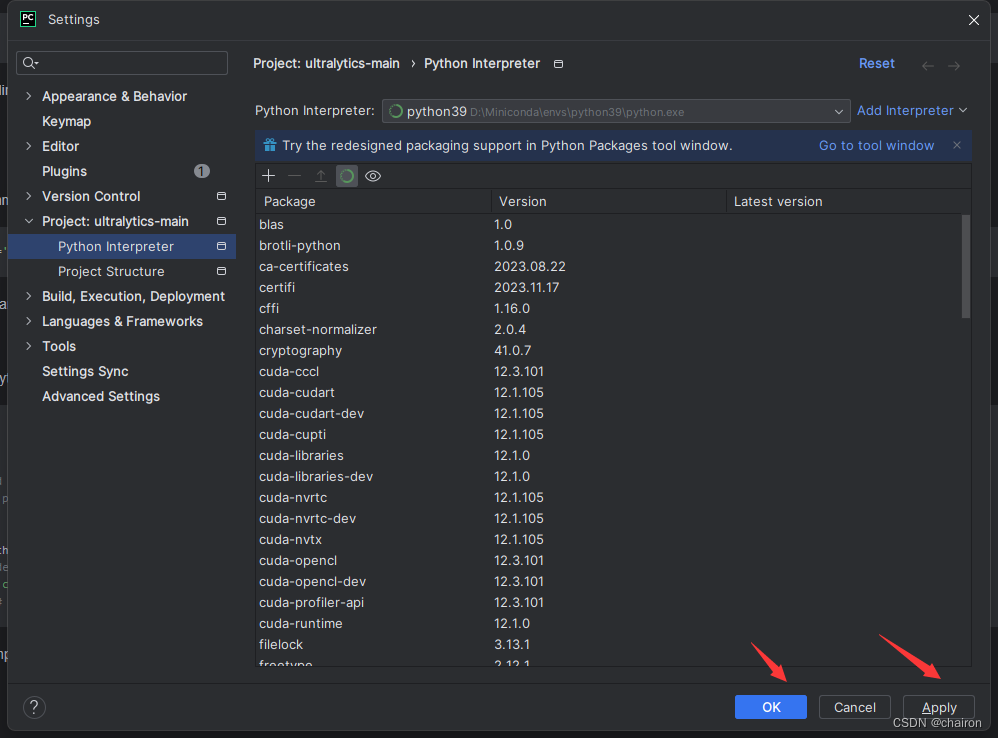
Windows11环境下配置深度学习环境(Pytorch)
目录 1. 下载安装Miniconda2. 新建Python3.9虚拟环境3. 下载英伟达驱动4. 安装CUDA版Pytorch5. CPU版本pytorch安装6. 下载并配置Pycharm 1. 下载安装Miniconda 下载安装包:镜像文件地址 将Miniconda相关路径添加至系统变量的路径中。 打开Anaconda Powershell Pr…...
泛型深入理解
泛型的概述 泛型:是JDK5中引入的特性,可以在编译阶段约束操作的数据类型,并进行检查。 泛型的格式:<数据类型>; 注意:泛型只能支持引用数据类型。 集合体系的全部接口和实现类都是支持泛型的使用的。 泛型的…...

Linux内核模块
文章目录 一、内核模块介绍二、模块讲解1、最简模块代码:2、模块三要素3、常用操作命令3.1、 lsmod:显示已加载模块状态3.2、 insmod:载入模块3.3、rmmod:卸载模块3.4、dmesg:显示信息3.5、modinfo:显示ker…...
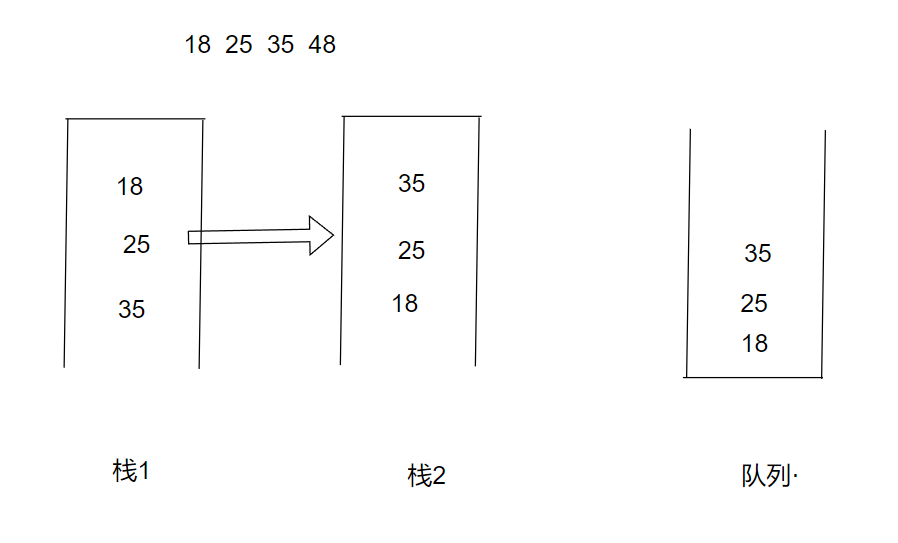
Java 栈和队列的交互实现
文章目录 队列和栈的区别一.用队列模拟实现栈1.1入栈1.2出栈1.3返回栈顶元素1.4判断栈是否为空 二.用栈模拟实现队列2.1 入队2.2出队2.3peek2.4判断队列是否为空 三.完整代码3.1 队列模拟实现栈3.2栈模拟实现队列 队列和栈的区别 栈和队列都是常用的数据结构,它们的…...

HarmonyOS应用开发者高级认证满分指南
声明:由于HarmonyOS应用开发者高级认证的题库一直在变,所以文章中的题目直做参考。 1. 判断题 云函数打包完成后,需要到APPGallery Connect创建对应函数的触发器才可以在端侧中调用。 【错】每一个自定义组件都有自己的生命周期。 【对】基…...

CSharp中Blazor初体验
Blazor 是一个由微软开发的开源 Web 框架,用于构建富客户端 Web 应用程序使用 C# 语言和 .NET 平台。Blazor 允许开发人员使用 C# 语言来编写前端 Web 应用程序,而不需要像传统的 JavaScript 框架(如 Angular、React 或 Vue.js)那…...

Linux下新建用户,并进行授权
注意:以下操作需要在root用户下! 新增用户 adduser 用户名设置密码 passwd 用户名更改目录所有者命令 chown -R 用户名:用户名 目录更改目录权限命令 chmod -R 755 目录...

STM32为基础的模拟I2C通用8bit和16bit读取以及多字节读取
GPIO模拟I2C驱动的通用代码,I2C的寄存器地址有8位和16位的,主要解决了同一个MCU同时处理8位和16位寄存器地址芯片时候的驱动问题。 typedef enum {IIC_8BIT_BASE_ADDR,IIC_16BIT_BASE_ADDR }iic_bits_e; typedef struct {uint8_t DevAddr;uint16_t RegA…...
算法训练营Day19
#Java #二叉树 #双指针 开源学习资料 Feeling and experiences: 二叉搜索树的最小绝对差:力扣题目链接 给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。 差值是一个正数,其数值等于两值之差的…...

C++数据结构——二叉搜索树详解
目录 一,关于二叉搜索树 1.1 概念 1.2 基本结构 二,二叉搜索树接口实现 2.1 插入 2.2 查找 2.3 打印 2.4* 删除 三,二叉搜索树接口递归实现 3.1 查找 3.2 插入 3.3 删除 四,二叉搜索树的默认成员函数 五,…...
ros2机器人在gazebo中移动方案
原文连接Gazebo - Docs: Moving the robot (gazebosim.org) 很重要的地方:使用虚拟机运行Ubuntu的时候,需要关闭”加速3D图形“的那个选项,否则gazebo无法正常显示。 Moving the robot(使用命令移动机器人示例) In t…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一)
宇树机器人多姿态起立控制强化学习框架论文解析 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(一) 论文解读:交大&港大&上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...

[C++错误经验]case语句跳过变量初始化
标题:[C错误经验]case语句跳过变量初始化 水墨不写bug 文章目录 一、错误信息复现二、错误分析三、解决方法 一、错误信息复现 write.cc:80:14: error: jump to case label80 | case 2:| ^ write.cc:76:20: note: crosses initialization…...