力扣题目学习笔记(OC + Swift)16. 最接近的三数之和
16. 最接近的三数之和
给你一个长度为 n 的整数数组 nums 和 一个目标值 target。请你从 nums 中选出三个整数,使它们的和与 target 最接近。
返回这三个数的和。
假定每组输入只存在恰好一个解。
排序 + 双指针
思路同15. 三数之和
简单地使用三重循环枚举所有的三元组时间复杂度为O(n^3),时间及空间复杂度均不满足我们使用的需求。
若我们枚举的三元组 (a,b,c) 满足a≤b≤c,保证了只有 (a,b,c)这个顺序会被枚举到,而 (b,a,c)、(c,b,a) 等等这些不会,这样就减少了重复。
可以发现,如果我们固定了前两重循环枚举到的元素 a和 b,那么只有唯一的 c满足 a+b+c≈target。当第二重循环往后枚举一个元素 b′ 时,由于 b′>b,那么满足 a+b′+c′≈target的 c′一定有 c′<c, c′在数组中一定出现在 c 的左侧。也就是说,我们可以从小到大枚举 b,同时从大到小枚举 c,即第二重循环和第三重循环实际上是并列的关系。
因此,我们就可以保持第二重循环不变,而将第三重循环变成一个从数组最右端开始向左移动的指针,这个思想就是「双指针」。每次遍历我们记录一个结果,和target比较,随着循环进行,我们的结果必然无限接近这个target值。
优化点:
1.每层遍历注意去除相邻重复的数字
2.若三数之和等于target,则直接返回,因为没有比相等更接近的了[😂]
3.设 i<cnt-2 && s = nums[i] + nums[i+1] + nums[i+2]。如果 s > target,由于数组已经排序,后面无论怎么选,选出的三个数的和不会比 s 还小,所以不会找到比 s 更优的答案了。所以只要 s > target,就可以直接 break 外层循环了。在 break 前判断 s 是否离 target 更近,如果更近,那么更新 best 为 s。
4.设 cnt > 1 && i<cnt-2 && s = nums[i] + nums[n-2] + nums[n-1]。如果 s < target,由于数组已经排序,nums[i] 加上后面任意两个数都不超过 s,所以下面的双指针就不需要跑了,无法找到比 s 更优的答案。但是后面还有更大的 nums[i],可能找到一个离 target 更近的三数之和,所以还需要继续枚举,continue 外层循环。在 continue 前判断 s 是否离 target 更近,如果更近,那么更新 best 为 s。
知识点:「双指针适用场景」当我们需要枚举数组中的两个元素时,如果我们发现随着第一个元素的递增,第二个元素是递减的,那么就可以使用双指针的方法,将枚举的时间复杂度从 O(n^2)降至O(n)。
总体时间复杂度:O(n^2), 排序时间复杂度为O(nlogn),渐进抵消
空间复杂度:O(logN)
Swift
func threeSumClosest(_ nums: [Int], _ target: Int) -> Int {let sortedNum = nums.sorted()let cnt = sortedNum.countvar result: Int = Int(1e7)let updateValue = {(sum:Int) inif sum == 2938 {print("")}if abs(sum-target) < abs(result-target) {result = sum;}}for i in 0..<cnt {if i>0 && sortedNum[i] == sortedNum[i-1] {continue}//由于有序,后面无论怎么选,选出的三个数的和不会比 s 还小if i<cnt-2 && sortedNum[i]+sortedNum[i+1]+sortedNum[i+2]>=target {updateValue(sortedNum[i]+sortedNum[i+1]+sortedNum[i+2]);break}//由于数组已经排序,nums[i] 加上后面任意两个数都不超过 s,所以下面的双指针就不需要跑了,但i增大后存在可能,因此继续外层if cnt > 1 && i<cnt-2 && sortedNum[i] + sortedNum[cnt-2] + sortedNum[cnt-1] < target {updateValue(sortedNum[i]+sortedNum[cnt-2]+sortedNum[cnt-1]);continue}var j=i+1, k=cnt-1while j < k {let s = sortedNum[i] + sortedNum[j] + sortedNum[k]if s == target {return target}updateValue(s);if s < target {var j0 = j+1;while j0<cnt && sortedNum[j0] == sortedNum[j0-1] {j0 += 1}j = j0}else {var k0 = k-1while k0 > 0 && sortedNum[k0] == sortedNum[k0+1] {k0 -= 1}k = k0}}}return result}
OC
-(NSInteger)threeSumClosest:(NSArray *)nums target:(NSInteger)target {if (nums.count < 3) {return 0;}//先排序NSArray *sortedNum = [nums sortedArrayUsingComparator:^NSComparisonResult(id _Nonnull obj1, id _Nonnull obj2) {return [obj1 compare:obj2];}];NSInteger cnt = sortedNum.count;__block NSInteger result = 1e7;void (^updateValue)(NSInteger) = ^(NSInteger sum) {if (labs(sum - target) < labs(result-target)) {result = sum;}};//开始遍历for (NSInteger i=0; i<cnt; i++) {//过滤重复的部分if (i>0 && sortedNum[i] == sortedNum[i-1]) {continue;}//由于有序,后面无论怎么选,选出的三个数的和不会比 s 还小if (i<cnt-2 && [sortedNum[i] integerValue] +[sortedNum[i+1] integerValue] + [sortedNum[i+2] integerValue] >= target) {updateValue([sortedNum[i] integerValue]+[sortedNum[i+1] integerValue] + [sortedNum[i+2] integerValue]);break;}//由于数组已经排序,nums[i] 加上后面任意两个数都不超过 s,所以下面的双指针就不需要跑了,但i增大后存在可能,因此继续外层if (cnt > 1 && i<cnt-2 && [sortedNum[i] integerValue] + [sortedNum[cnt-2] integerValue]+ [sortedNum[cnt-1] integerValue] < target) {updateValue([sortedNum[i] integerValue]+[sortedNum[cnt-2] integerValue]+[sortedNum[cnt-1] integerValue]);continue;}NSInteger j=i+1, k=cnt-1;while (j<k) {NSInteger s = [sortedNum[i] integerValue] + [sortedNum[j] integerValue] + [sortedNum[k] integerValue];if (s == target) {return s;}updateValue(s);if(s < target) {NSInteger j0 = j+1;//过滤重复的部分while (j0 < cnt && [sortedNum[j0] integerValue] == [sortedNum[j0-1] integerValue]) {j0++;}j = j0;}else {NSInteger k0 = k-1;while (k0 > 0 && [sortedNum[k0] integerValue] == [sortedNum[k0+1] integerValue]) {k0--;}k = k0;}}}return result;
}
相关文章:
16. 最接近的三数之和)
力扣题目学习笔记(OC + Swift)16. 最接近的三数之和
16. 最接近的三数之和 给你一个长度为 n 的整数数组 nums 和 一个目标值 target。请你从 nums 中选出三个整数,使它们的和与 target 最接近。 返回这三个数的和。 假定每组输入只存在恰好一个解。 排序 双指针 思路同15. 三数之和 简单地使用三重循环枚举所有的三…...

基于STM32的DHT11温湿度传感器与LCD显示器的集成设计
在本文中,我们将详细介绍如何基于STM32微控制器实现DHT11温湿度传感器与LCD显示器的集成设计。我们将包括硬件连接、软件编程以及涉及的STM32库函数和相关知识。这个项目旨在帮助您理解如何使用STM32来读取DHT11温湿度传感器的数据,并将数据显示在LCD显示…...

解决浏览器自动将http跳转至https导致无法访问的问题
以下只针对Chrome浏览器 方法一: 1.地址栏中输入chrome://net-internals/#hsts。 2.在Delete domain中输入项目的域名,并Delete(删除)。 3.可以在Query domain测试是否删除成功。 HSTS全称:HTTP Strict Transport Se…...

小程序面试题 | 07.精选小程序面试题
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...

深度学习的推理部分
深度学习的推理部分指的是已经训练好的深度学习模型应用于新数据(通常是测试或实际应用数据)以进行预测、分类、分割等任务的过程。在深度学习中,训练和推理是两个阶段: 训练阶段: 在这个阶段,深度学习模型…...
如何用 CleanMyMac 来保护 Mac 隐私
大家早上好,中午好,下午好,晚上好。 在我们使用MacBook上的自带浏览器-Safari(或者一些其他浏览器)进行网页浏览的时候,往往会留下一些痕迹。如果这些痕迹涉及一些敏感数据信息的话,那么我们肯…...
opencv入门到精通——鼠标事件和Trackbar控件的使用
目标 了解如何在OpenCV中处理鼠标事件 您将学习以下功能:cv.setMouseCallback() 了解将轨迹栏固定到OpenCV窗口 您将学习以下功能:cv.getTrackbarPos,cv.createTrackbar等。 简单演示 在这里,我们创建一个简单的应用程序&am…...

iOS 收集 SDK 内部 log
为 SDK 设置 log 等级,设置 RCIMClient 的 logLevel 为您期望的,可以在 SDK initWithAppkey 之后设置,比如希望只收集错误 log,那么可以设置为 RC_Log_Level_Error,如果想一般信息、警告信息,错误信息都收集…...
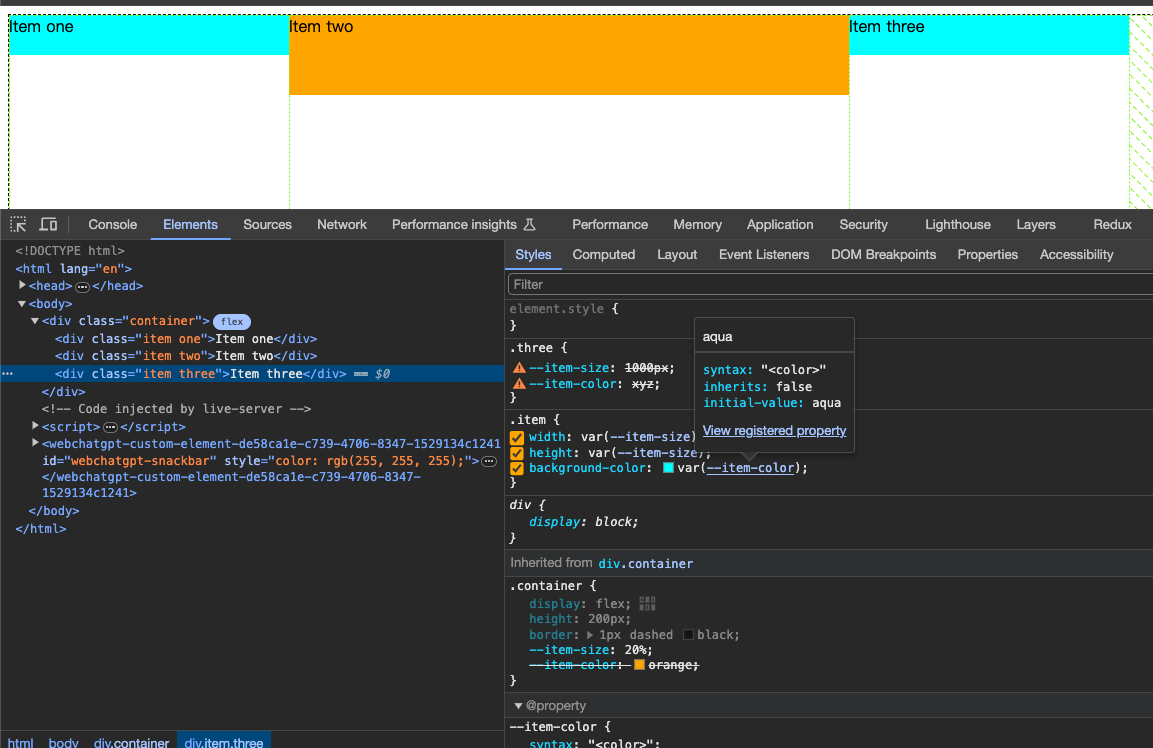
【CSS @property】CSS自定义属性说明与demo
CSS property property - CSS: Cascading Style Sheets | MDN At 规则 - CSS:层叠样式表 | MDN Custom properties (–*): CSS variables - CSS: Cascading Style Sheets | MDN CSS Houdini - Developer guides | MDN 📚 什么是property? property CSS…...

【华为数据之道学习笔记】6-3数据服务分类与建设规范
数据服务是为了更好地满足用户的数据消费需求而产生的,因此数据消费方的差异是数据服务分类的最关键因素。具体包括两大类:数据集服务和数据API服务。 1. 数据集服务 (1)数据集服务定义 比较常见的数据消费者有两类:一…...

Vue的脚手架
脚手架配置 脚手架文档:Vue CLI npm config set registry https://registry.npm.taobao.org vue.config.js配置选项: 配置参考 | Vue CLI ref选项 ref和id类似,给标签打标识。 document.getElementById(btn); this.$ref.btn; 父子组…...

Java实现Word中插入上标和下标
Java实现Word中插入上标和下标 Java不能直接在Word中插入上标和下标,但是可以通过POI库来实现。 下面提供一个Java代码示例,使用POI库向Word中插入带有上标和下标的文字: import org.apache.poi.xwpf.usermodel.XWPFDocument; import org.…...

Java和Python中的目标堆栈规划实现
目标堆栈规划是一种简单高效的人工智能规划算法,用于解决复合目标问题。它的工作原理是**将总体目标分解为更小的子目标,然后以向后的顺序逐一解决它们。 让我们考虑一个简单的例子来说明目标堆栈规划。想象一下你想要烤一个蛋糕,目标是准备…...
后管系统登录后隐藏url上信息同时获取url上携带参数~开发需求(bug)总结7)
(前端)后管系统登录后隐藏url上信息同时获取url上携带参数~开发需求(bug)总结7
问题描述: 首先我这个后管项目是若依权限管理系统,路由实现都是动态加载的。现在有一个需求,后端会邮件发送系统中的链接,这个链接是携带参数(id、用户的加密信息),比如:https://47.23.12.1/task/list?id…...

CSS3新增样式
1,圆角边框 在CSS3中,新增了圆角边框样式,这样我们的盒子就可以变圆角了 border-radious属性用于设置元素的外边框圆角 语法: border-radious:length; radious 半径(圆的半径)原理…...
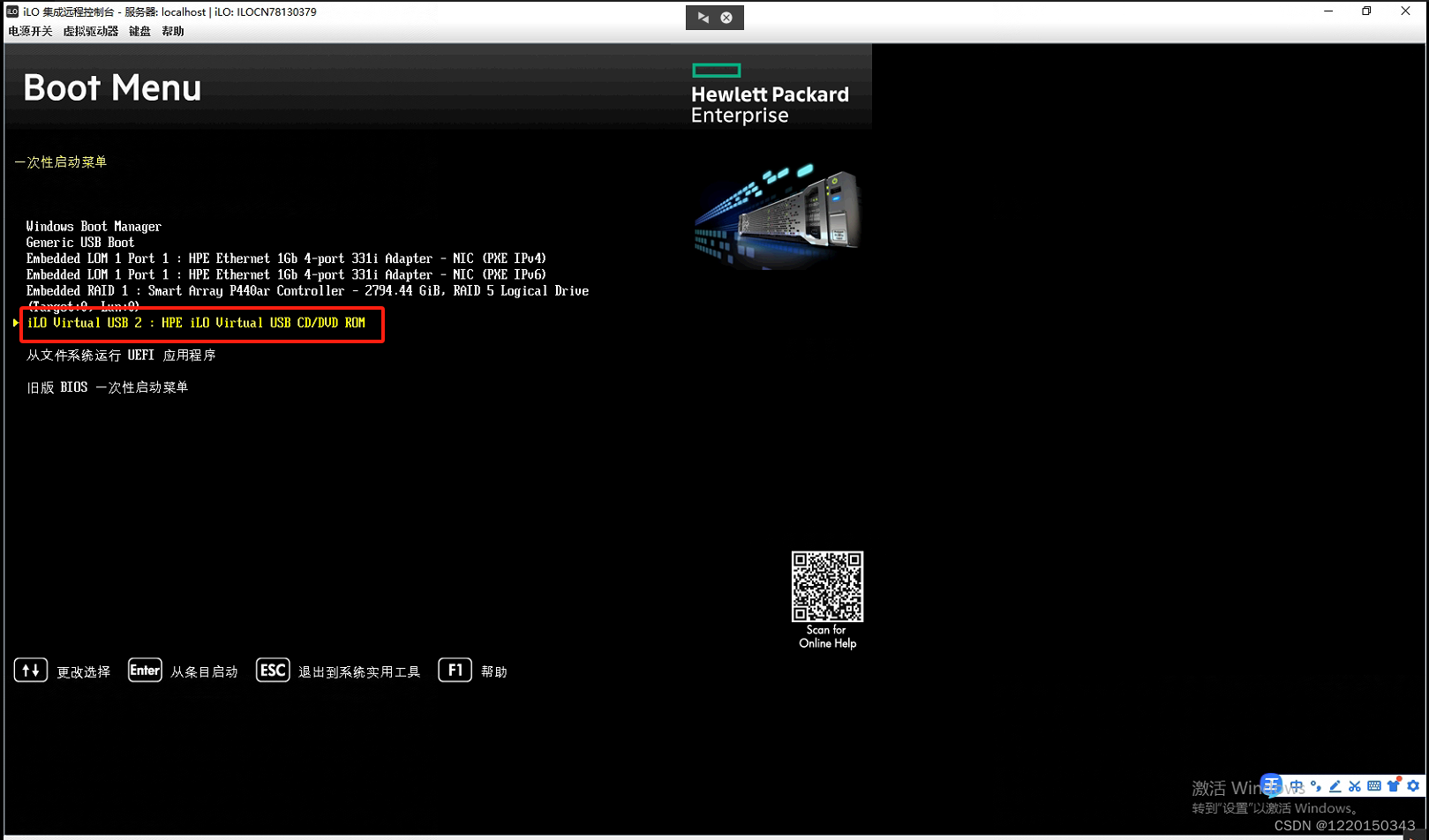
HP服务器idrac设置以及系统安装
HP服务器idrac设置以及系统安装 一、设置管理口的地址和密码1、HP服务器重新界面选择"F9"进入BIOS,设置iLo5(idrac)的IP和用户名密码。2、选择"系统配置"。3、选择"iLO 4"配置程序。4、网络选项是设置idrac管理口的地址,设…...

rpc和消息队列区别
RPC 和消息队列都是分布式微服务系统中重要的组件之一,下面我们来简单对比一下两者: 从用途来看:RPC 主要用来解决两个服务的远程通信问题,不需要了解底层网络的通信机制。通过 RPC可以帮助我们调用远程计算机上某个服务的方法&a…...
.)
Permission denied (publickey,gssapi-keyex,gssapi-with-mic).
当使用ssh登录服务器时,由于文件权限没有设置报以下错误 WARNING: UNPROTECTED PRIVATE KEY FILE! Permissions for test_1.pem are too open. It is required that your private key files are NOT accessible by others. This private key will be ignored. Loa…...
虚幻学习笔记18—C++委托(多播)和事件
一、前言 委托分单播和多播,多播就是可以绑定多个回调函数,然后一次性执行。这样也可以理解为啥多播没有返回值,多个回调函数执行后返回哪一个都是问题啊。而事件呢官方官方文档说法是“对于事件而言,只有定义事件的类才能调用 Br…...
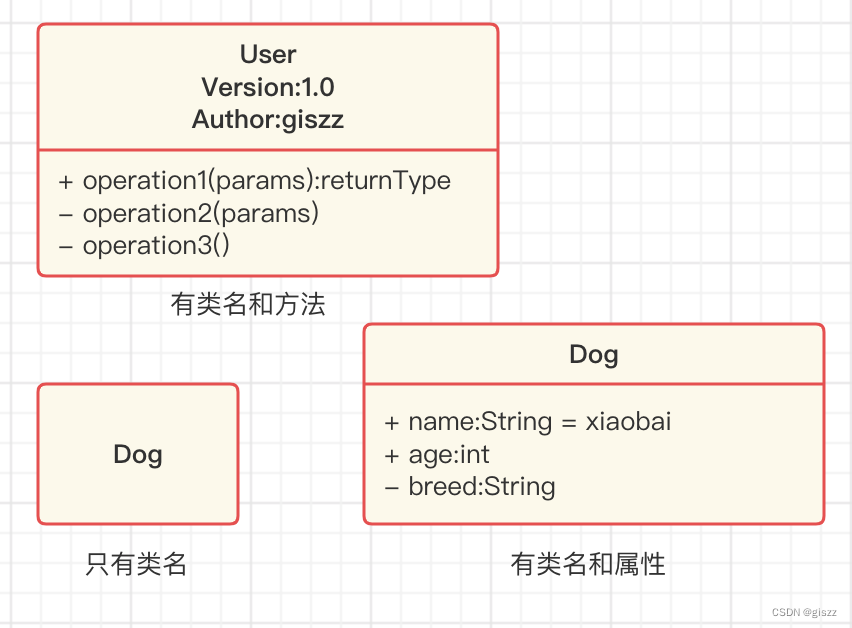
【UML】第9篇 类图
目录 一、类图的概念 二、类图的主要作用 三、类图的构成 3.1 类的名称 3.2 抽象类(Abstract Class) 一、类图的概念 类图是UML模型中静态视图。它用来描述系统中的有意义的概念,包括具体的概念、抽象的概念、实现方面的概念等。静态视…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...
