深入浅出堆排序: 高效算法背后的原理与性能

📋 前言
🌈堆排序一个基于二叉堆数据结构的排序算法,其稳定性和排序效率在八大排序中也是名列前茅。
⛳️堆我们已经讲解完毕了,今天就来深度了解一下堆排序是怎么实现的以及为什么他那么高效。
📚本期文章收录在《数据结构&算法》,大家有兴趣可以看看呐!
⛺️ 欢迎铁汁们 ✔️ 点赞 👍 收藏 ⭐留言 📝!
文章目录
- 📋 前言
- 一、堆排序的思想概念
- 二、堆排序的两种实现方式
- 2.1 向上取整
- 2.2 向下取整
- 三、堆排序的实现代码
- 3.1 如何利用向上调整建堆
- 3.1 如何利用向下调整建堆
- 3.3 堆建完了如何排序数据
- 3.4 堆排完整代码
- 四、俩种实现方式的效率对比
- 4.1 向上调整建堆时间复杂度计算
- 4.2 向下调整建堆时间复杂度计算
- 4.3 对比结果
- 4.4 堆的时间复杂度计算
- 📝文章结语:
一、堆排序的思想概念
堆排序可以说是排序算法中比较高效的了,既稳定又高效。既然叫堆排序那么肯定离不来堆,基于二叉树来进行构建:
- 不知道大家发现过没有堆有一个特性
- 要不就是最大值(大堆)要不然就是一个最小值(小堆)
而我们吧堆顶最大值或最小值进行 pop删除并取出每次的 最大值或者最小值把这些值存储起来
之后他的数据是不是也排序完了,而我们又是用数组来存储的删除不就是把下标 减减吗?
二、堆排序的两种实现方式
堆排序的核心思想就是利用堆的特性来进行数据的取出每次都是最大值或者最小值,那么我得到一组数据要进行堆排序首先:
- 这组数据需要时堆才能进行排序,那么我们就要开始建堆就完了。
建堆的方法一共有俩种分别是向下取整和向上取整这里都给大家介绍一下
2.1 向上取整
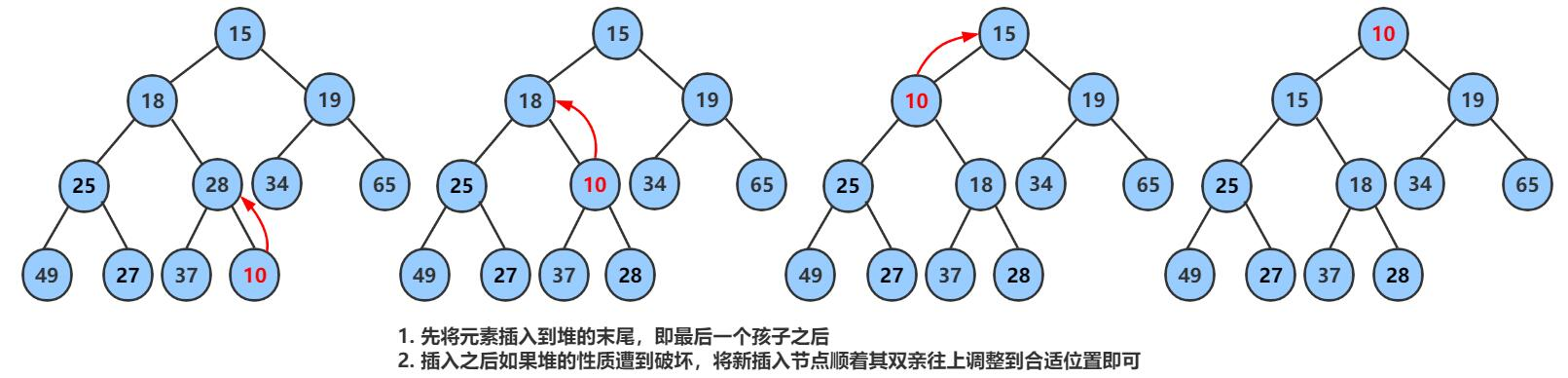
向上取整就是,把新的数据尾插到堆里面然后把他和父节点进行对比调整:
- 数组存储这里有一个特点
parent = (child-1)/ 2 ; - 父节点等于子节点
-1除二
📚 代码演示:
//向上调整
void adjustup(HeapTypeData* a, int child)
{int parent = (child - 1) / 2;while (child > 0){//建小堆if (a[child] < a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}}
2.2 向下取整
向下取整的思想就是把堆顶数据左右子树的的数值进行对比然后向下进行调整:
- 🔥 向下调整算法有一个前提:左右子树必须是一个堆,才能调整
- 这里由于是数组存储的所以堆的左右子树都是
child = parent* 2+1;- 孩子节点的左节点都等于 父节点
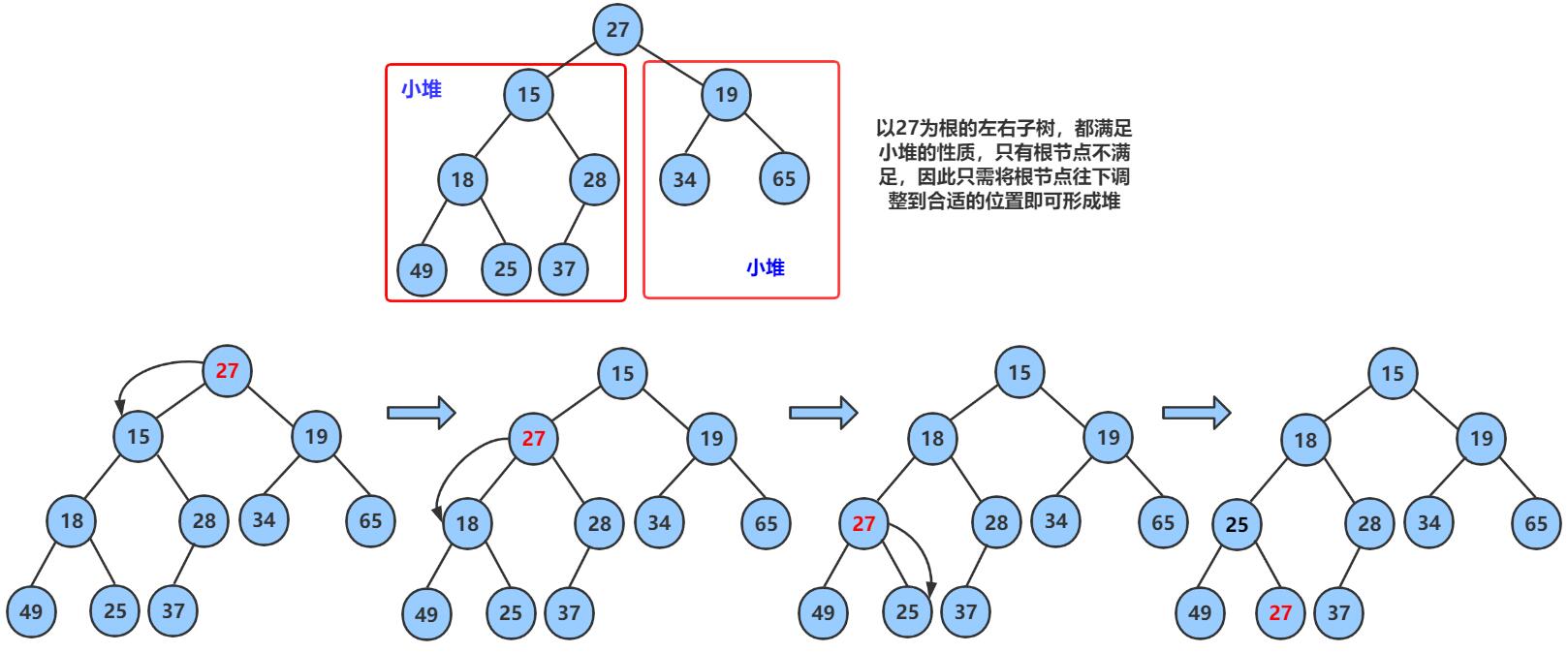
如果堆顶数据和左右子树对比 ,然后再进行调整数据
📚 代码演示:
//向下调整
void adjustdown(HeapTypeData* a, int n, int parent)
{int child = parent* 2+1;while (child < n){if (child+1 < n && a[child + 1] < a[child]){child++;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent*2 +1;}else{break;}}
}
三、堆排序的实现代码
3.1 如何利用向上调整建堆
向上调整的思想大家都懂了,而建堆的话我们可以这样想:
- 从数据的第一个数每次向上调整这样
- 当调整到最后一个数的时候前面所有的都是已经调整好的堆
📚 代码演示:
//向上调整
void adjustup(HeapTypeData* a, int child)
{int parent = (child - 1) / 2;while (child > 0){//建小堆if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}}
//向上调整建堆 OR 建小堆降序
// 建大堆升序
for (int i = 1; i < n; i++)
{adjustup(a, i);
}
3.1 如何利用向下调整建堆
利用向下调整建堆的要求是左右俩边都是堆才可以向下调整:
-
那么我们可以把他分为
分治子问题先向下调整左右子树的在一部部调整堆顶 -
而堆的最后一个子树一定是堆
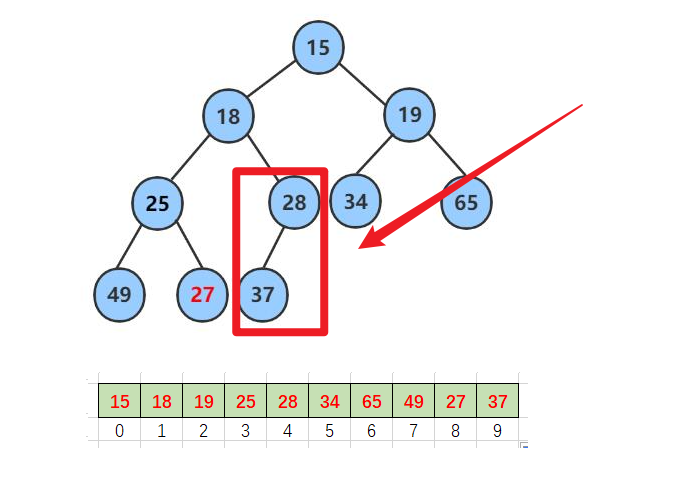
这样我们就可以利用数组存储堆的特性 父节点等于子节点 -1除2
parent = (child-1)/ 2 ;- 然后再利用循环 减减 把每个子树都调整完到堆顶堆就减好了
📚 代码演示:
//向下调整
void adjustdown(HeapTypeData* a, int n, int parent)
{int child = parent* 2+1;while (child < n){if (child+1 < n && a[child + 1] > a[child]){child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent*2 +1;}else{break;}}
}//向上调整建堆 OR 建小堆降序
// 建大堆升序
for (int i = (n-1-1)/2; i > 0; i--)
{adjustdown(a, n, i);
}
3.3 堆建完了如何排序数据
堆我们建完了,排序难道一个个把堆顶数据取出然后再放进去吗? 当然不是排序算法都是在数组的 原本空间上进行排序:
- 我们的思想还是和删除 POP 一样先把堆顶的数据和堆底进行交换
- 然后再利用下标减减删除数据,(虚拟删除其实还在)
- 这样每次最大或者最小的数据都被按规律放在原空间里面了
📚 代码演示:
//开始排序int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);adjustdown(a, end, 0);end--;}
3.4 堆排完整代码
//向上调整
void adjustup(HeapTypeData* a, int child)
{int parent = (child - 1) / 2;while (child > 0){//建小堆if (a[child] > a[parent]){Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}}
//向下调整
void adjustdown(HeapTypeData* a, int n, int parent)
{int child = parent* 2+1;while (child < n){if (child+1 < n && a[child + 1] > a[child]){child++;}if (a[child] > a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent*2 +1;}else{break;}}
}void HeapSort(int* a, int n)
{//向上调整建堆 OR 建小堆降序 // 建大堆升序/*for (int i = 1; i < n; i++){adjustup(a, i);}*/for (int i = (n-1-1)/2; i > 0; i--){adjustdown(a, n, i);}//开始排序int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);adjustdown(a, end, 0);end--;}
}
四、俩种实现方式的效率对比
4.1 向上调整建堆时间复杂度计算

4.2 向下调整建堆时间复杂度计算
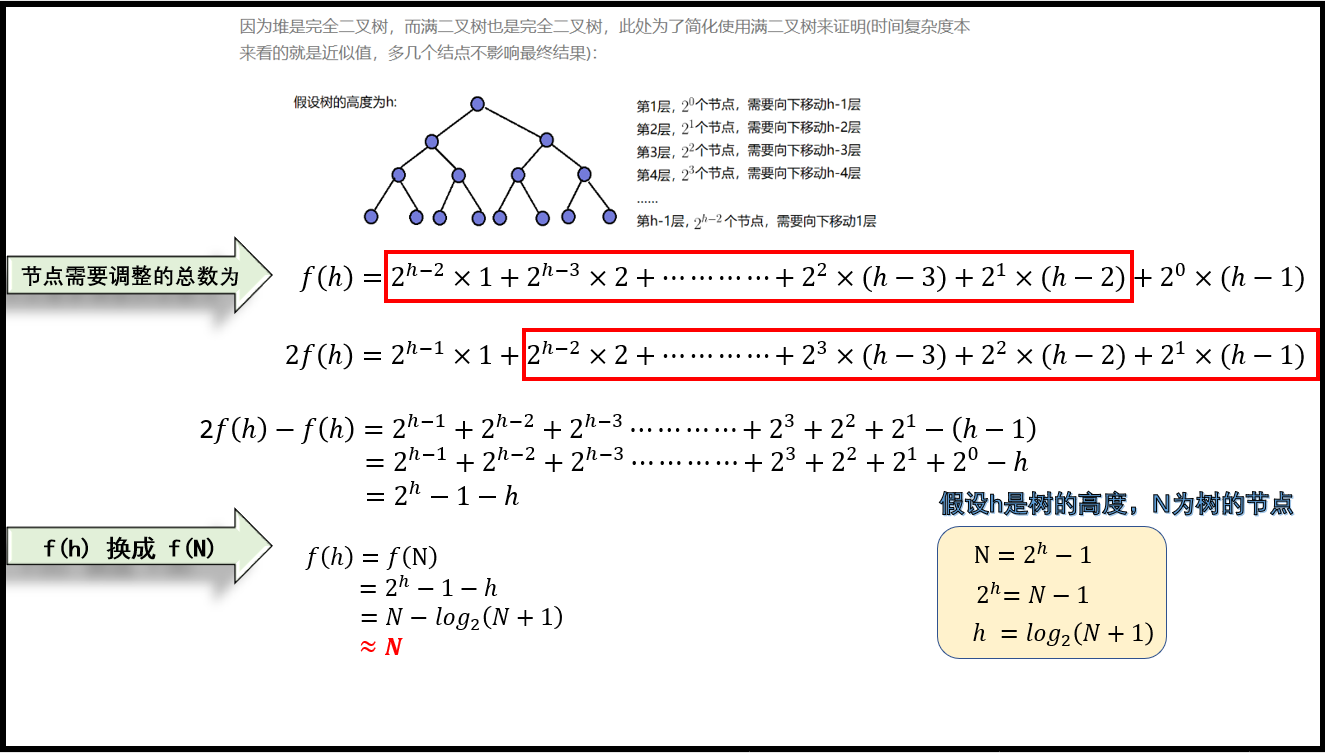
4.3 对比结果
| 建堆思想 | 时间复杂度 |
|---|---|
| 向上调整建堆 | O(N * logN) |
| 向下调整建堆 | O(N) |
🔥 所以我们在进行堆排序的时候一定首先选取向下调整算法时间复杂度更优。
- 假设有1000万个数据
| 建堆思想 | 排序次数 |
|---|---|
| 向上调整 | 1000W*24(约等于 2亿多) |
| 向下调整 | 1000W |
所以我们向下调整的算法是远远大于向上调整的这是为什么呢?
- 🔥 因为 向下调整最后一层节点多且全部需要调整到第一层(调整h-1次)
- 🔥 而向下调整 最后一层不需要调整,越是接近底层调整越少
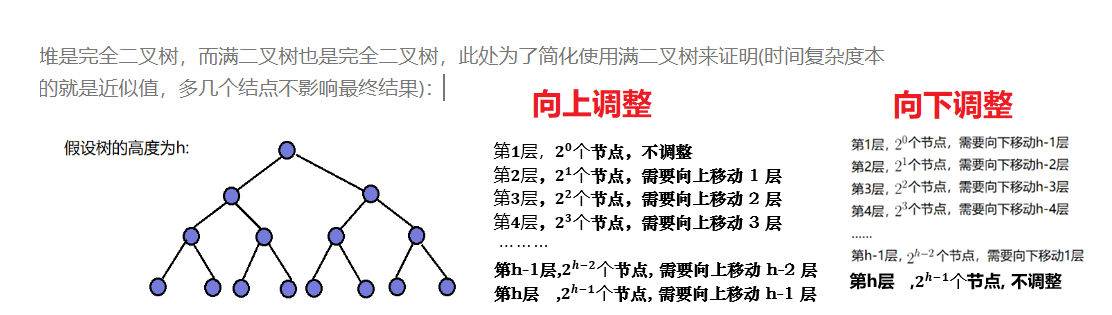
4.4 堆的时间复杂度计算
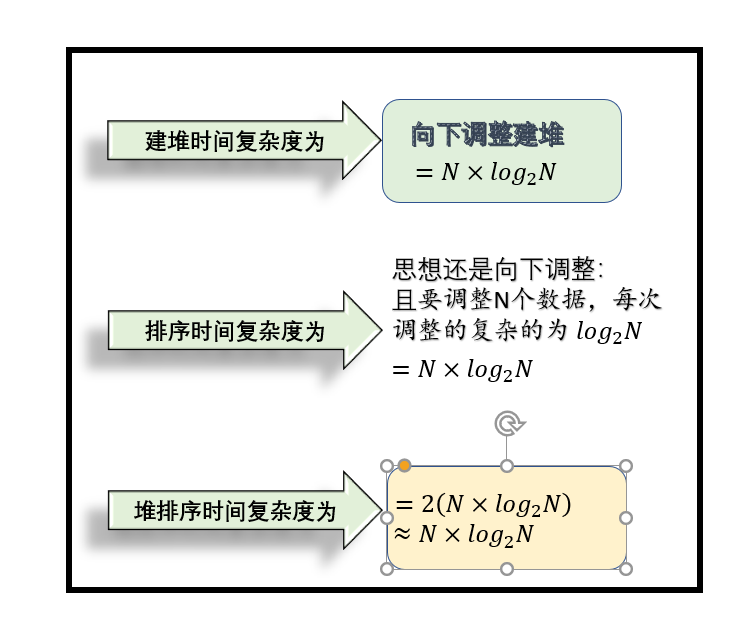
📝文章结语:
☁️ 以上就是本章的全部内容了,各位铁汁们快去试试吧!
看到这里了还不给博主扣个:
⛳️ 点赞☀️收藏 ⭐️ 关注!
💛 💙 💜 ❤️ 💚💓 💗 💕 💞 💘 💖
拜托拜托这个真的很重要!
你们的点赞就是博主更新最大的动力!
有问题可以评论或者私信呢秒回哦。

相关文章:

深入浅出堆排序: 高效算法背后的原理与性能
🎬 鸽芷咕:个人主页 🔥 个人专栏: 《linux深造日志》 《高效算法》 ⛺️生活的理想,就是为了理想的生活! 📋 前言 🌈堆排序一个基于二叉堆数据结构的排序算法,其稳定性和排序效率在八大排序中也…...

Golang实践录:gin绑定解析json的两种方法
本文介绍 Golang 的 gin 框架接收json数据并解析的2种方法。 起因及排查 某微服务工程,最近测试发现请求超时,由于特殊原因超时较短,如果请求处理耗时超过1秒则认为失败。排查发现,可能是gin接收解析json数据存在耗时,…...

Hypervisor Display架构
Hypervisor Display架构部分 1,所有LA侧的APP与显示相关的调用最终都会交由SurfaceFlinger处理 2,SurfaceFlinger会最终调用android.hardware.graphics.composer2.4-service服务 3,android.hardware.graphics.composer2.4-service服务会调用G…...
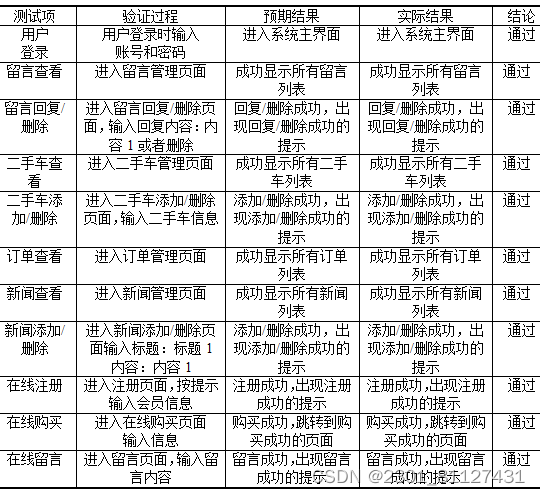
基于ssm二手车交易平台的设计论文
摘 要 进入21世纪网络和计算机得到了飞速发展,并和生活进行了紧密的结合。目前,网络的运行速度以达到了千兆,覆盖范围更是深入到生活中的角角落落。这就促使二手交易网站的发展。二手交易网站可以实现远程购物,远程选择喜欢的商品…...

IDEA 设置 SpringBoot logback 彩色日志(附配置文件)
1、背景说明 最开始使用 SpringBoot 时,控制台日志是带彩色的,让人眼前一亮😄 后来彩色莫名丢失,由于影响不大,一直没有处理。 2、配置彩色 最近找到了解决方法(其实是因为自定义 logback.xml࿰…...

数学建模学习笔记-皮尔逊相关系数
内容:皮尔逊相关系数 一.概念:是一个和线性线关的相关性系数 1.协方差概念: 协方差受到量纲的影响因此需要剔除 2.相关性的误区 根据这个结论,我们在计算该系数之前需要确定是否为线性函数 二.相关性的计算 1.Matlabÿ…...

随笔:集成学习:关于随机森林,梯度提升机的东拉西扯
1.集成学习 这里不会描述算法过程。 当我们有许多学习器对同一个任务做出判断,他们预测的概率可能各不相同,比如预测一个男生(小徐)会不会喜欢另一个女生(小雪),支持向量机算出来小徐爱上小雪的概率是0.8,朴素贝叶斯认为是0.3&a…...
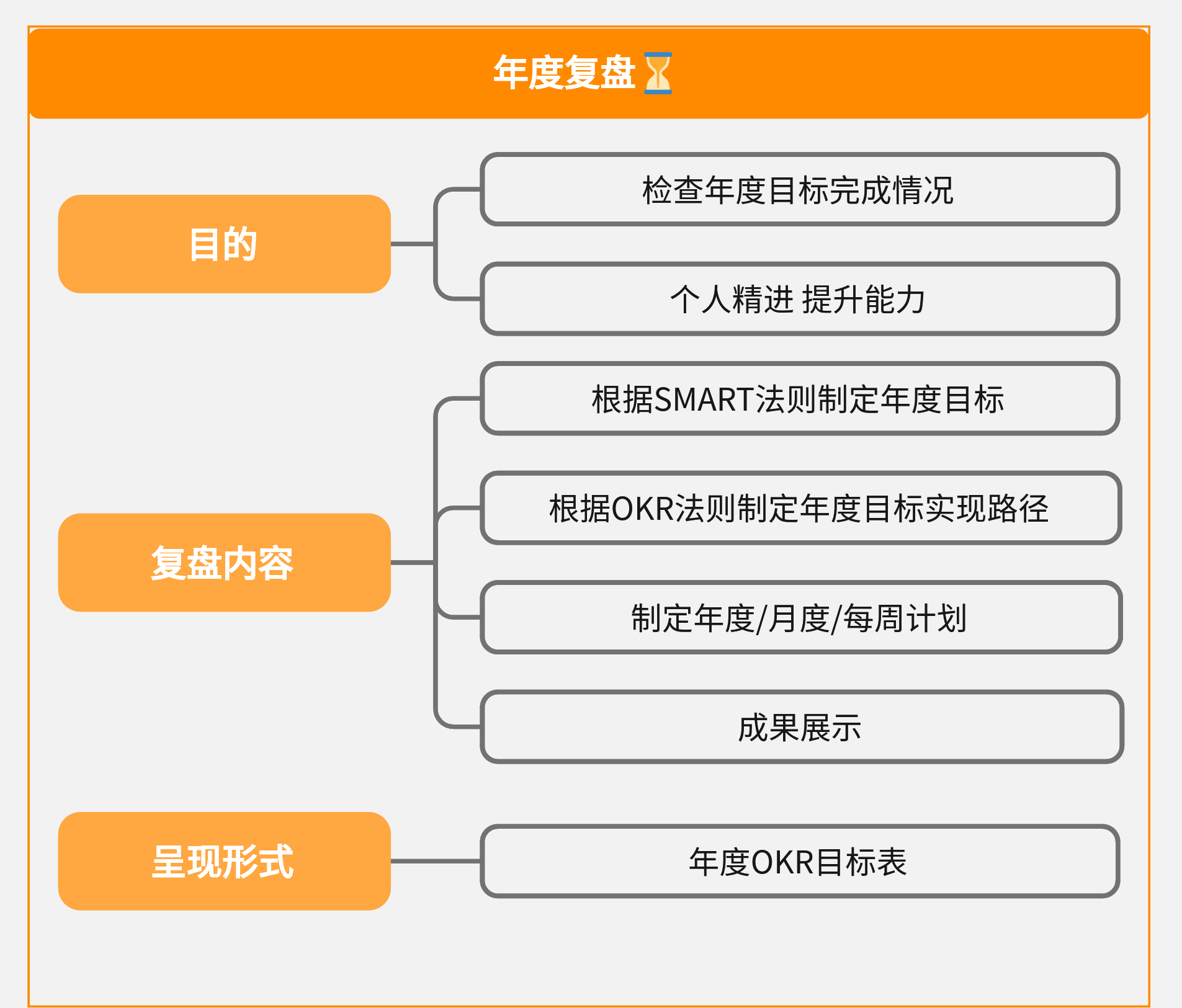
多款实用个人年终总结模板,助力你的年度汇报!
临近年末,相信很多职场人这阵子都在忙着撰写个人年终总结,这份材料是对自己过去一年的工作进行的回顾和总结。撰写年终总结,其实也是一个非常重要的自我反思过程,可以帮助我们明确自己的目标,找出需要改进的地方&#…...
【C语言】动态内存管理基础知识——动态通讯录,如何实现通讯录容量的动态化
引言 动态内存管理的函数有:malloc,calloc,ralloc,free,本文讲解动态内存函数和使用,如何进行动态内存管理,实现通讯录联系人容量的动态化,对常见动态内存错误进行总结。 ✨ 猪巴戒:个人主页✨ 所属专栏:《C语言进阶》…...
配置Let‘s Encrypt (免费https证书))
Centos9(Stream)配置Let‘s Encrypt (免费https证书)
1. 安装snap,用来安装certbot: sudo dnf install epel-release sudo dnf upgrade sudo yum install snapd sudo systemctl enable --now snapd.socket sudo ln -s /var/lib/snapd/snap /snap snap install core snap refresh core 2. 安装 certbot命令…...
)
Spring之事务(2)
学习的最大理由是想摆脱平庸,早一天就多一份人生的精彩;迟一天就多一天平庸的困扰。各位小伙伴,如果您: 想系统/深入学习某技术知识点… 一个人摸索学习很难坚持,想组团高效学习… 想写博客但无从下手,急需…...

嵌入式科普(5)ARM GNU Toolchain相关概念和逻辑
一、目的/概述 二、资料来源 三、逻辑和包含关系 四、Arm GNU Toolchain最常用的命令 嵌入式科普(5)ARM GNU Toolchain相关概念和逻辑 一、目的/概述 对比高集成度的IDE(MDK、IAR等),Linux开发需要自己写Makefile等多种脚本。eclipse、Visual Studio等需要了解预处…...

Elasticsearch:什么是文本分类?
文本分类定义 - text classification 文本分类是一种机器学习,它将文本文档或句子分类为预定义的类或类别。 它分析文本的内容和含义,然后使用文本标签为其分配最合适的标签。 文本分类的实际应用包括情绪分析(确定评论中的正面或负面情绪&…...
指针(3)
C语言昂,指针昂,最喜欢的一集,小时候学这一课我直接取地址了。上一篇博客给大家讲解了不同类型的指针变量的大小,今天来给大家讲解一下根据其所产生的一些性质。(往期回顾:指针(2)-C…...

外汇天眼:我碰到外汇投资骗局了吗?学会这5招,轻松识别外汇诈骗黑平台!
近年来外汇市场因为交易量大、流动性大、不容易被控盘、品种简单、风险相对低等特色,因此吸引不少投资人青睐,成为全球金融市场的热门选择。 然而,市面上充斥许多诈骗集团设立的黑平台,也打着投资外汇的名义行骗,不免会…...
一文解析子网掩码和默认网关,成为网络设置达人
随着互联网的普及,越来越多的人开始接触并使用电脑和网络。然而,对于很多初学者来说,网络设置中的子网掩码和默认网关是两个相对陌生的概念。今天,我们就来深入解析这两个概念,让你轻松掌握网络设置技巧! …...

二分查找法详解(6种变形)
前言 在之前的博客中,我给大家介绍了最基础的二分查找法(没学的话点我点我!) 今天我将带大家学习二分法的六种变形如何使用,小伙伴们,快来开始今天的学习吧! 文章目录 1,查找第一个…...

uniapp uview 页面多个select组件回显处理,默认选中
<view class"add-item column space-around" click"selectClick(1)"><text class"w-s-color-3 f-28">商品分类</text><view class"w-100 space-between"><!-- 第一个参数为你的单选数组,第二个…...
linux中playbook的控制语句
本章主要介绍 playbook中的控制语句。 使用 when 判断语句 block-rescue判断 循环语句 一个play中可以包含多个task,如果不想所有的task全部执行,可以设置只有满足某个 条件才执行这个task,不满足条件则不执行此task。本章主要讲解when 和 …...

MongoDB介绍
一、MongoDB介绍 1.1 mongoDB介绍 MongoDB 是由C语言编写的,是一个基于分布式文件存储的开源数据库系统。 在高负载的情况下,添加更多的节点,可以保证服务器性能。 MongoDB 旨在为WEB应用提供可扩展的高性能数据存储解决方案。 MongoDB …...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...
