数据结构：图文详解 树与二叉树（树与二叉树的概念和性质，存储，遍历）

---

目录

一.树的概念

二.树中重要的概念

三.二叉树的概念

满二叉树

完全二叉树

四.二叉树的性质

五.二叉树的存储

六.二叉树的遍历

前序遍历

中序遍历 

后序遍历 

---

一.树的概念

树是一种非线性数据结构，它由节点和边组成。树的每个节点可以有零个或多个子节点，其中一个节点被指定为根节点。树的节点之间通过边连接。另外，树形结构中，子树之间不能有交集，否则就不是树形结构。

树的结构具有层级关系，根节点位于最顶层，而叶节点位于最底层。树的形状可以类比于现实生活中的树，根节点相当于树的根部，而分支和叶子节点则相当于树的枝干和叶子。

在计算机科学中，树被广泛用于各种应用，例如文件系统、数据库索引、编译器中的抽象语法树等。树的常见特点是具有唯一的根节点、没有循环的边、可以有任意数量的子节点等。

树的常见操作包括插入新节点、删除节点、查找节点、遍历节点等。常见的树结构包括二叉树、红黑树、AVL树等。树的设计和使用在算法和数据结构领域中非常重要，它可以提供高效的数据存储和检索方式。 

---

二.树中重要的概念

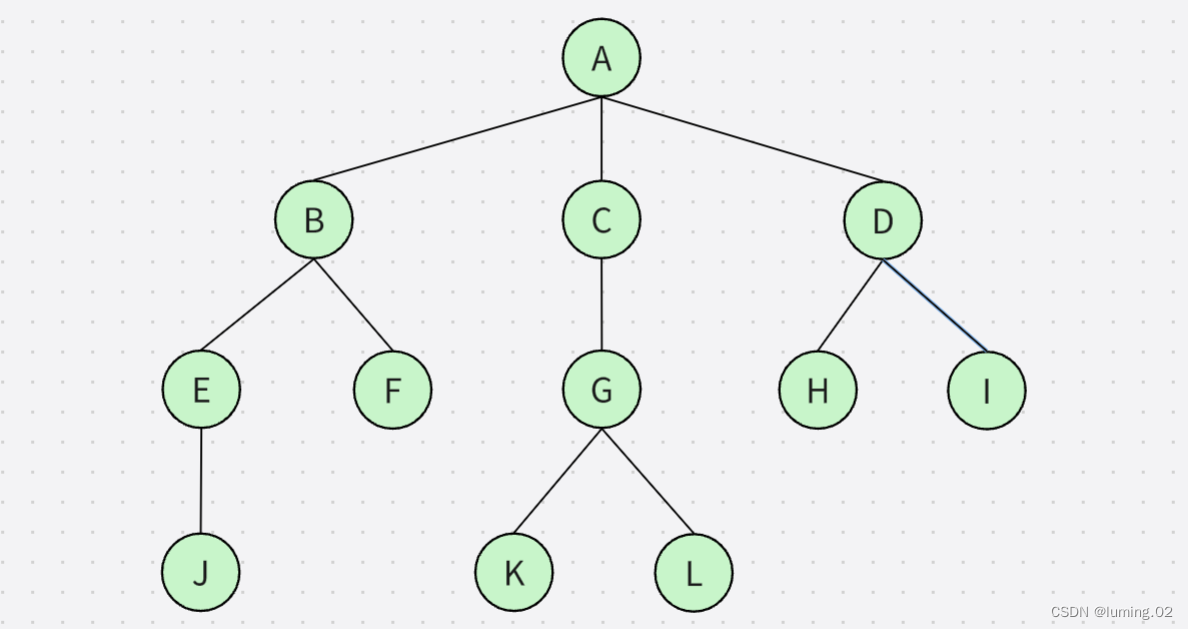
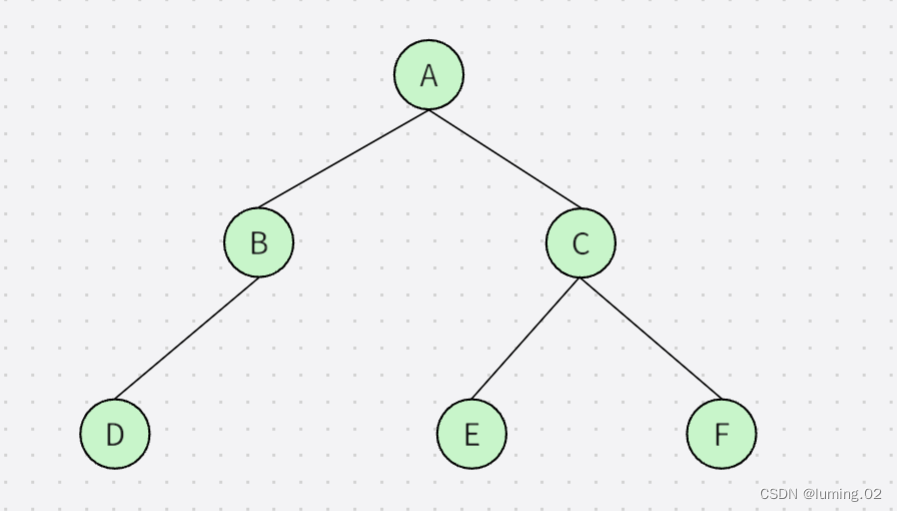
笔者就以下图作为例子进行说明：

• 结点的度：一个结点含有子树的个数称为该结点的度； 如上图：A的度为6
• 树的度：一棵树中，所有结点度的最大值称为树的度； 如上图：树的度为6
• 叶子结点或终端结点：度为0的结点称为叶结点； 如上图：B、C、H、I...等节点为叶结点
• 双亲结点或父结点：若一个结点含有子结点，则这个结点称为其子结点的父结点； 如上图：A是B的父结点
• 孩子结点或子结点：一个结点含有的子树的根结点称为该结点的子结点； 如上图：B是A的孩子结点
• 根结点：一棵树中，没有双亲结点的结点；如上图：A
• 结点的层次：从根开始定义起，根为第1层，根的子结点为第2层，以此类推
• 树的高度或深度：树中结点的最大层次； 如上图：树的高度为4
• 非终端结点或分支结点：度不为0的结点； 如上图：D、E、F、G...等节点为分支结点
• 兄弟结点：具有相同父结点的结点互称为兄弟结点； 如上图：B、C是兄弟结点
• 堂兄弟结点：双亲在同一层的结点互为堂兄弟；如上图：H、I互为兄弟结点
• 结点的祖先：从根到该结点所经分支上的所有结点；如上图：A是所有结点的祖先
• 子孙：以某结点为根的子树中任一结点都称为该结点的子孙。如上图：所有结点都是A的子孙
• 森林：由m（m>=0）棵互不相交的树组成的集合称为森林 

---

三.二叉树的概念

二叉树是一种常见的树状数据结构，在二叉树中，每个节点最多有两个子节点，分别称为左子节点和右子节点。二叉树的特点是每个节点最多只有两个子节点，且子节点的位置是有序的，即左子节点在右子节点之前。

二叉树可以为空，如果一个二叉树不为空，则它一定由根节点、左子树和右子树组成。每个节点都有一个值，可以是任意类型的数据。

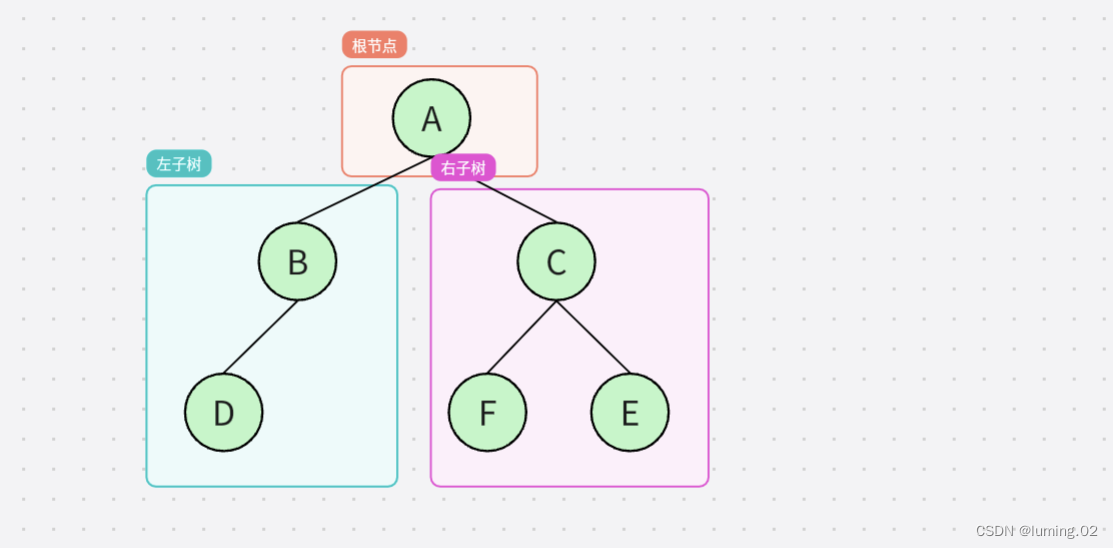
二叉树也可以只有一个节点，如下图所示，根节点不为空，但是左子树和右子树为空，这样的二叉树也是允许存在的

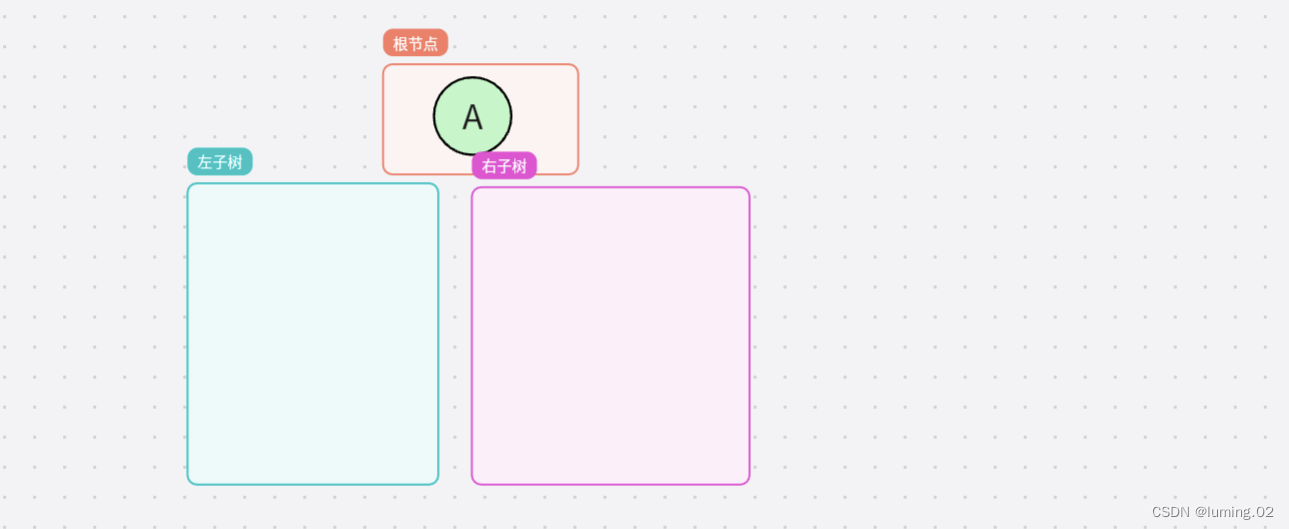
总的来说，对于任意一颗二叉树，它都是由以下几部分复合而成的：

二叉树可以用来表示许多实际问题，例如计算机科学中的排序和搜索算法。在二叉树中，有一些特殊的类型，如满二叉树、完全二叉树和平衡二叉树等。二叉树还可以通过遍历算法来访问其中的节点，最常见的遍历算法有前序遍历、中序遍历和后序遍历。

二叉树中还有以下俩个常见的特殊的二叉树

满二叉树

一棵二叉树，如果每层的结点数都达到最大值，则这棵二叉树就是满二叉树。也就是说，如果一棵二叉树的层数为 k ，且结点总数是 ，则它就是满二叉树。

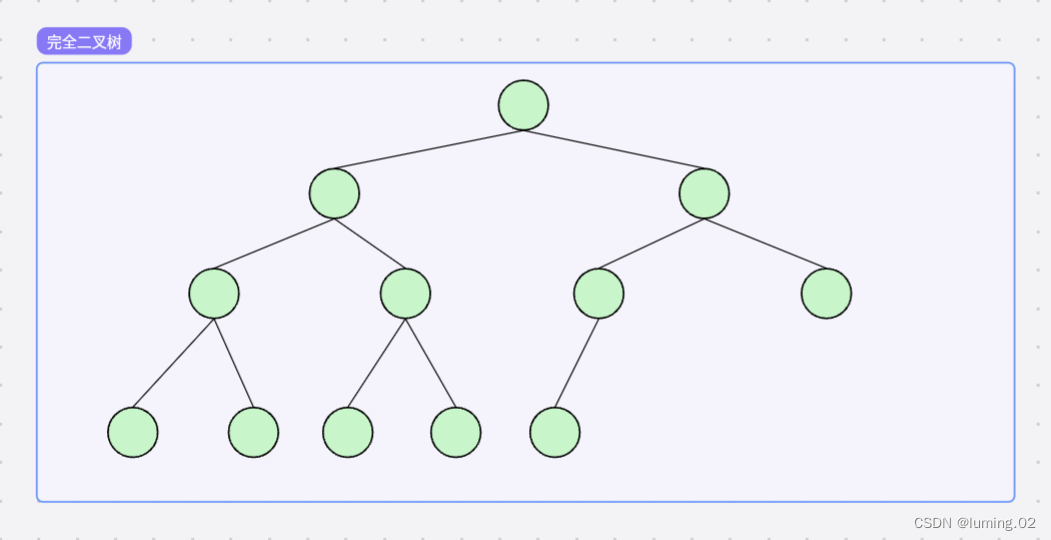
完全二叉树

完全二叉树是由满二叉树而引出来的，对于深度为 k 的，有 n 个结点的二叉树，当且仅当其每一个结点都与深度为 k 的满二叉树中编号从0至n-1的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树

---

四.二叉树的性质

1. 若规定根结点的层数为1，则一棵非空二叉树的第 i 层上最多有个节点
2. 若规定只有根结点的二叉树的深度为 1 ，则深度为K的二叉树的最大结点数是
3. 对任何一棵二叉树, 如果其叶结点个数为 n0 , 度为2的非叶结点个数为 n2 ,则有 n0＝n2＋1 
4.  具有 n 个结点的完全二叉树的深度 k 为
5. 对于具有 n 个结点的完全二叉树，如果按照从上至下从左至右的顺序对所有节点从0开始编号，则对于序号为 i 的结点有：若i>0，双亲序号：(i-1)/2；i=0，i为根结点编号，无双亲结点；若2i+1<n，左孩子序号：2i+1，否则无左孩子；若2i+2<n，右孩子序号：2i+2，否则无右孩

---

五.二叉树的存储

对于任意一个节点，我们最多只能知道它的左右孩子节点和根节点，以及自己保存的数据，由此我们引申出许多种表示二叉树的方法，常见的有孩子表示法，孩子双亲表示法，兄弟节点表示法...

// 孩子表示法
class Node {int val; // 数据域Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树
}// 孩子双亲表示法
class Node {int val; // 数据域Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树Node parent; // 当前节点的根节点
}

笔者以下图举例：

 

我们使用孩子表示法，然后依次按照图示组成一颗二叉树（后文的遍历都是基于此树）

public class MyBinaryTree {public class TreeNode {public char val;//记录当前节点的值public TreeNode leftNode;//记录当前节点的左孩子节点public TreeNode rightNode;//记录当前节点的右孩子节点public TreeNode(char val) {//初始化节点的值this.val = val;}}//生成每一个节点,然后连起来public TreeNode CreatTree() {TreeNode A = new TreeNode('A');TreeNode B = new TreeNode('B');TreeNode C = new TreeNode('C');TreeNode D = new TreeNode('D');TreeNode E = new TreeNode('E');TreeNode F = new TreeNode('F');TreeNode G = new TreeNode('G');TreeNode H = new TreeNode('H');//依次按照图示连起来A.leftNode = B;A.rightNode = C;B.leftNode = D;C.leftNode = E;C.rightNode = F;//最后返回根节点return A;}
}

---

六.二叉树的遍历

二叉树的遍历是指按照一定的规则，将二叉树中的所有节点访问一次，并且每个节点只访问一次。常见的二叉树遍历方式有前序遍历、中序遍历和后序遍历。

前序遍历

前序遍历（preorder traversal）：先访问根节点，然后遍历左子树，最后遍历右子树。具体步骤如下：

1. 访问根节点
2. 前序遍历左子树
3. 前序遍历右子树 

代码实现如下：

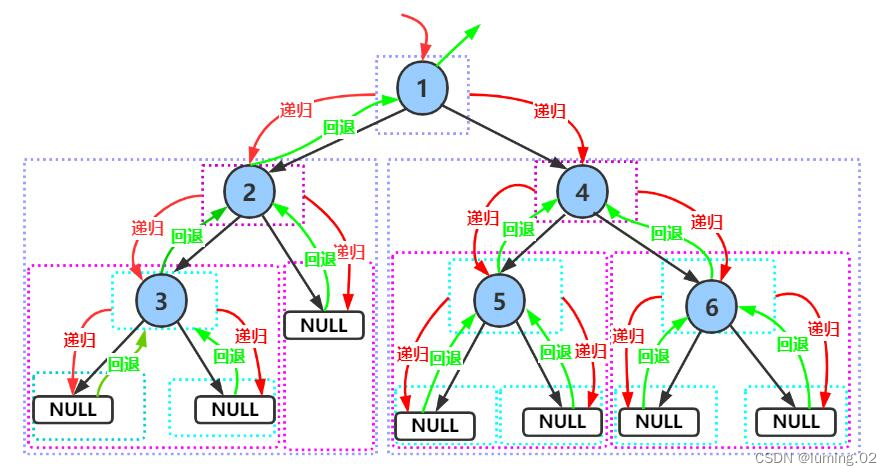
    //前序遍历public void preOrder(TreeNode root) {if (root == null) {return;//空树不需要遍历}System.out.print(root.val + " ");//访问根节点preOrder(root.leftNode);//前序遍历左子树preOrder(root.rightNode);//前序遍历右子树}

对于上述的代码，程序运行起来的具体逻辑是如下图这样的，反复的递归和回退进行实现

 

中序遍历 

中序遍历（inorder traversal）：先遍历左子树，然后访问根节点，最后遍历右子树。具体步骤如下：

1. 中序遍历左子树
2. 访问根节点
3. 中序遍历右子树

代码实现如下：

    //中序遍历public void inOrder(TreeNode root) {if (root == null) {return;//空树不需要遍历}inOrder(root.leftNode);//中序遍历左子树System.out.print(root.val + " ");//访问根节点inOrder(root.rightNode);//中序遍历右子树}

后序遍历 

后序遍历（postorder traversal）：先遍历左子树，然后遍历右子树，最后访问根节点。具体步骤如下：

1. 后序遍历左子树
2. 后序遍历右子树
3. 访问根节点

代码实现如下：

    //后序遍历public void postOrder(TreeNode root) {if (root == null) {return;//空树不需要遍历}postOrder(root.leftNode);//后序遍历左子树postOrder(root.rightNode);//后序遍历右子树System.out.print(root.val + " ");//访问根节点}

我们可以写个测试来看看遍历的结果：

public class Test {public static void main(String[] args) {MyBinaryTree myBinaryTree = new MyBinaryTree();MyBinaryTree.TreeNode rootNode = myBinaryTree.CreatTree();System.out.println();System.out.println("前序遍历：");myBinaryTree.preOrder(rootNode);System.out.println();System.out.println("中序遍历:");myBinaryTree.inOrder(rootNode);System.out.println();System.out.println("后序遍历:");myBinaryTree.postOrder(rootNode);}
}

输出：

也就是说：

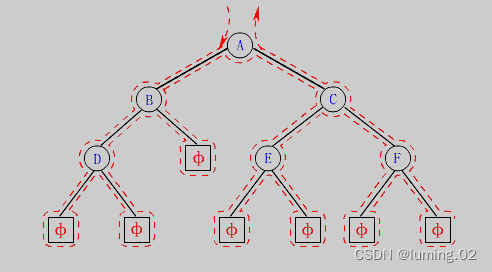
其实不管是前序，中序，后序遍历，他们整体的搜索过程都是一样的，不同的地方在于对当前根节点的处理时间不一样：前序遍历是先处理根节点；中序遍历是先遍历当前节点的左子树再处理当前根节点；而后序遍历则是最后再处理根节点，就像下图一样

以上是三种最基本的二叉树遍历方式。除了这三种，还有一些其他的二叉树遍历方式，比如层序遍历、螺旋遍历等。不同的遍历方式适用于不同的场景和问题，可以根据具体的需求选择合适的遍历方式。

---

---

---

  本次的分享就到此为止了，希望我的分享能给您带来帮助，也欢迎大家三连支持，你们的点赞就是博主更新最大的动力！如有不同意见，欢迎评论区积极讨论交流，让我们一起学习进步！有相关问题也可以私信博主，评论区和私信都会认真查看的，我们下次再见