当前位置： 首页 > news >正文

实用学习网站和资料

news 2026/2/10 17:53:03

github:https://github.com/GitHubDaily/GitHubDaily

Linux操作手册：

GitHub - abarrak/linux-sysops-handbook: Essentials of Linux system administration.

从零开始制作一个操作系统：

GitHub - ruiers/os-tutorial-cn: 从零开始编写一个操作系统教程 -- 中文版

标准 C++ 算法指南完整版：

GitHub - HappyCerberus/book-cpp-algorithms: The Standard Algorithms in C++.

Hello,算法：

GitHub - krahets/hello-algo: 《Hello 算法》：动画图解、一键运行的数据结构与算法教程，支持 Java, C++, Python, Go, JS, TS, C#, Swift, Rust, Dart, Zig 等语言。

像黑客一样使用命令行：

https://github.com/xuxiaodong/usingcli-book

Arch Linux简明指南;

https://github.com/NakanoMikuOrg/arch-guide

LeetCode 题解仓库：

GitHub - doocs/leetcode: 🔥LeetCode solutions in any programming language | 多种编程语言实现 LeetCode、《剑指 Offer（第 2 版）》、《程序员面试金典（第 6 版）》题解

《命令行速览》：

GitHub - vastutsav/command-line-quick-reference: quick reference on command line tools and techniques for the people with limited time

Hackinq C++： 一份颇为全面的 C++ 速查表与信息图表。覆盖了算法、随机分布、序列、Lambda 表达式、设计指南等内容。

C++ Cheat Sheets & Infographics | hacking C++

《C++ Concurrency in Action 2ed笔记》
C++11/14/17/20 多线程，掌握操作系统原理，解锁并发编程技术。原书籍前五章介绍了线程支持库的基本用法，后六章从实践角度介绍了并发编程的设计思想。

   sqliteviz：GitHub 上一款比较实用的开源工具，可为 SQLite 数据库快速生成可视化图表，支持导入 CSV 和 JSON 文件，可离线使用。

《Linux 设备驱动开发详解》(宋宝华) 学习笔记

相关文章：

实用学习网站和资料

github:https://github.com/GitHubDaily/GitHubDaily Linux操作手册： GitHub - abarrak/linux-sysops-handbook: Essentials of Linux system administration. 从零开始制作一个操作系统： GitHub - ruiers/os-tutorial-cn: 从零开始编写一个操作系统…...

编程日记 2023/12/26 19:30:42

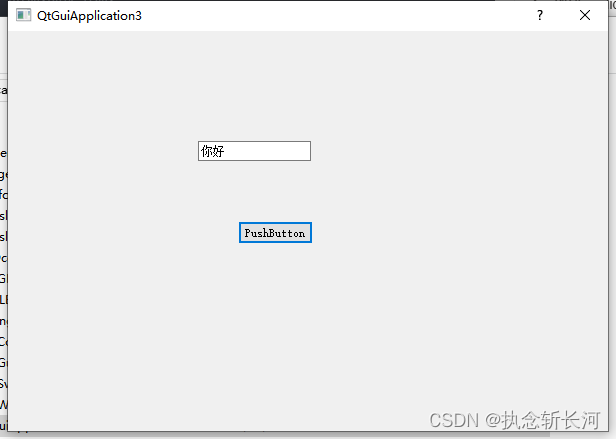
【已解决】c++qt如何制作翻译供程序调用

本博文源于笔者正在编写的工具需要创建翻译文件，恰好将qt如何进行翻译，从零到结果进行读者查阅，并非常推荐读者进行收藏点赞，因为步步都很清晰，堪称胎教式c制作，而且内容还包括如何部署在windows下。堪称值…...

编程日记 2023/12/26 19:26:37

DPDK单步跟踪(3)-如何利用visual studio 2019和visual gdb来单步调试dpdk

准备工作 因为时间的关系，我想到哪说到哪，可能没那么高的完成度。 但其实有心的人，看到这个标题，就关了本文自己能做了。 why和how to build debug version DPDK,见前两篇。这里我们准备开始。 首先，你有一台linux机…...

编程日记 2023/12/26 19:23:35

Python爬虫---解析---BeautifulSoup

BeautifulSoup简称：bs4 作用：解析和提取数据 1. 安装：pip install bs4 或pip install bs4 -i https://pypi.douban.com/simple（使用国内镜像下载） 注意：需要安装在python解释器相同的位置,例如&#xf…...

编程日记 2023/12/26 19:21:33

Argument list too long when copying files

for i in /path/to/dir/*; do cp "$i" /path/to/other/dir/; done...

编程日记 2023/12/26 19:20:32

configure

configure 配置软件./configure --prefix$PWD/output CCaarch64-linux-gcc --hostaarch64-linux --enable-shared --enable-staticconfig.sub 文件 这个文件用于确定主机系统的类型，并返回与该系统相关的标识符。它包含一系列 shell 函数，用于检测主机…...

编程日记 2023/12/26 19:18:30

HOJ 项目部署-前端定制 默认勾选显示标签、 在线编辑器主题和字号大小修改、增加一言功能 题目AC后礼花绽放

# 项目拉取地址： https://gitee.com/himitzh0730/hoj.git # 切换到hoj-vue目录执行以下命令 #安装依赖 npm install #运行服务 npm run serve #修改代码后构建项目到dist文件夹，到服务器docker-compose.yml中修改hoj-frontend文件映射即可 npm run build…...

编程日记 2023/12/26 19:17:29

Scikit-Learn线性回归(二)

Scikit-Learn线性回归二：多项式回归 1、多项式回归2、多项式回归的原理3、Scikit-Learn多项式回归3.1、Scikit-Learn多项式回归API1、多项式回归 线性回归研究的是一个自变量与一个因变量之间的回归问题。在实际应用中，并不是所有的情景都符合线性关系，大多数情况都是非线性…...

编程日记 2023/12/26 19:16:28

07 Vue3框架简介

文章目录 一、Vue3简介1. 简介2. 相关网站3. 前端技术对比4. JS前端框架5. Vue核心内容6. 使用方式 二、基础概念1. 创建一个应用2. 变量双向绑定（v-model）3. 条件控制（v-if）4. 数组遍历（v-for）5. 绑定事件…...

编程日记 2023/12/26 19:15:27

前端八股文（js篇）

一.强制类型转换规则 首先需要了解隐式转换所调用的函数。 当程序员显示调用Boolean（value）,Number（value），String（value）完成的类型转换，叫做显示类型转换。 当通过new Boolean&…...

编程日记 2023/12/26 19:13:24

windows+ubuntu离线安装翻译软件有道词典

背景： 某些情况下，需要在无法连接互联网的电脑上翻译单词，句子以及段落，就需要能离线安装和翻译的翻译软件，具备一定的词库量，目前找到了《有道词典》。 windows 亲测，无法联网的win10中安装…...

编程日记 2023/12/26 19:11:20

DevC++ easyx实现视口编辑，在超过屏幕大小的地图上画点，与解决刮刮乐bug效果中理解C语言指针的意义

继上篇文案， DevC easyx实现地图拖动，超过屏幕大小的巨大地图的局部显示在屏幕的方法——用悬浮窗的原理来的实现一个视口-CSDN博客 实现了大地图拖动，但是当时野心不止，就想着一气能搓啥就继续搓啥，看着地图移动都搓…...

编程日记 2023/12/26 19:01:12

Kali Linux—借助 SET+MSF 进行网络钓鱼、生成木马、获主机shell、权限提升、远程监控、钓鱼邮件等完整渗透测试（一）

社会工程学—世界头号黑客凯文米特尼克在《欺骗的艺术》中曾提到，这是一种通过对受害者心理弱点、本能反应、好奇心、信任、贪婪等心理陷阱进行诸如欺骗、伤害等危害手段。 SET最常用的攻击方法有：用恶意附件对目标进行 E-mail 钓鱼攻击、Java Applet攻…...

编程日记 2023/12/26 19:00:11

时间与时间戳转换及android和ios对时间识别的区别

注意： "2021-05-01 12:53:59.55" 时间对象在 ios 中会出现 NaN-NaN1-NaN 需要将对象格式化为："2021/05/01 12:53:59.55" 可同时兼容 android 和 ios。 //将某时间转时间戳 /* var time new Date("2021-05-01 12:53:59.55&qu…...

编程日记 2023/12/26 18:57:09

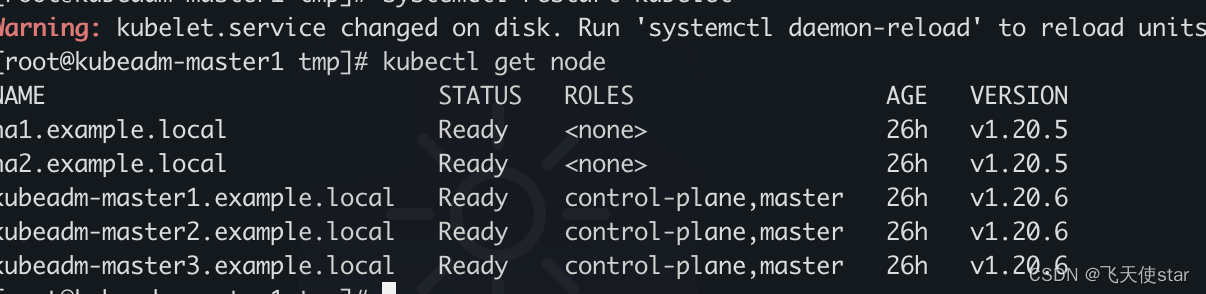
飞天使-k8s知识点7-kubernetes升级

文章目录 验证新版本有没有问题需要安装的版本微微 1.20.6.0kubeadm upgrade plan 验证新版本有没有问题 查看可用版本的包 现有的状态 查看版本 yum list kubeadm --showduplicates |grep 1.20 yum list kubelet --showduplicates |grep 1.20 yum list kubectl --showduplic…...

编程日记 2023/12/26 18:50:02

【Unity游戏制作】游戏模型导入之前需要注意的三个基本点

👨‍💻个人主页：元宇宙-秩沅 👨‍💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨‍💻 本文由 秩沅 原创 👨‍💻 收录于专栏：Uni…...

编程日记 2023/12/26 18:49:01

三列布局 css

实现如下图的三列布局： .box {width:1400px;margin:0 auto;padding-bottom:40px;> .left {float:left;width:180px;margin-top:100px;text-align:center;}> .center {float:left;margin-top:100px;margin-left:130px;item-box {float:left;text-align:left;…...

编程日记 2023/12/26 18:42:57

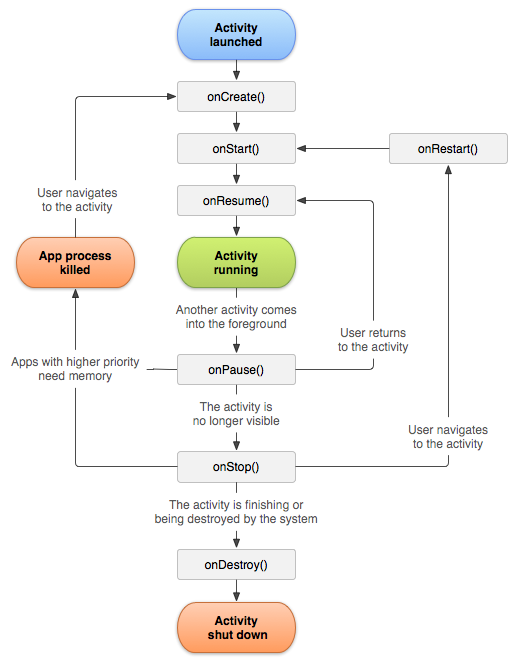
Android开发之生命周期（App、Activity）

在Android开发中，应用程序（App）和活动（Activity）的生命周期是非常重要的概念。它们各自都有一系列的生命周期方法，这些方法会在特定的时刻被系统自动调用，以便于开发者对应用或活动进行相应的操…...

编程日记 2023/12/26 18:39:54

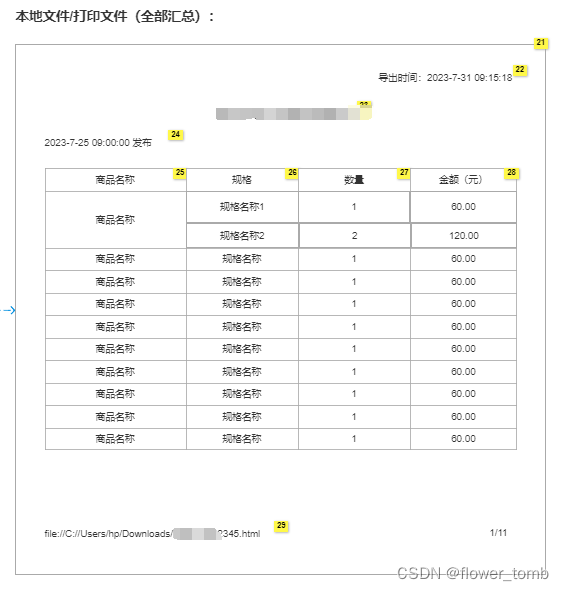
利用html2Canvas将表格下载为html

给到我的需求是点击按钮时请求后端接口，根据后端返回的数据，生成表格,并将表格的内容直接下载为html,如下图。 平常做的下载都是后端返回二进制流，这次前端做下载那就必须把页面先画出来，因为下载下来的表格在页面上是不显示的&a…...

编程日记 2023/12/26 18:38:53

《Git快速入门》Git分支

1.master、origin、origin/master 区别 首先搞懂git分支的一些名称区别： master ： Git 的默认分支名字。它并不是一个特殊分支、跟其它分支完全没有区别。 之所以几乎每一个仓库都有 master 分支，是因为 git init 命令默认创建它&#xff0c…...

编程日记 2023/12/26 18:36:52

【python异步多线程】异步多线程爬虫代码示例

claude生成的python多线程、异步代码示例，模拟20个网页的爬取，每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程：允许程序同时执行多个任务，提高IO密集型任务（如网络请求）的效率…...

编程新知 2025/12/16 18:04:55

Android 之 kotlin 语言学习笔记三（Kotlin-Java 互操作）

参考官方文档：https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java（供 Kotlin 使用） 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

编程新知 2026/2/8 0:33:04

学习STC51单片机32（芯片为STC89C52RCRC）OLED显示屏2

每日一言 今天的每一份坚持，都是在为未来积攒底气。 案例：OLED显示一个A 这边观察到一个点，怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 ： 如果代码里信号切换太快（比如 SDA 刚变，SCL 立刻变&#…...

编程新知 2026/2/6 0:50:24

项目部署到Linux上时遇到的错误（Redis，MySQL，无法正确连接，地址占用问题）

Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败，具体原因是客户端发送了密码认证请求，但Redis服务器未设置密码 1.为Redis设置密码（匹配客户端配置） 步骤： 1）.修…...

编程新知 2026/2/8 14:19:47

均衡后的SNRSINR

本文主要摘自参考文献中的前两篇，相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程，其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt​ 根发送天线， n r n_r nr​ 根接收天线的 MIMO 系…...

编程新知 2026/1/30 4:47:24

深度学习习题2

1.如果增加神经网络的宽度，精确度会增加到一个特定阈值后，便开始降低。造成这一现象的可能原因是什么？ A、即使增加卷积核的数量，只有少部分的核会被用作预测 B、当卷积核数量增加时，神经网络的预测能力会降低 C、当卷…...

编程新知 2026/1/26 5:53:30

初探Service服务发现机制

1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能：服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源&#xf…...

编程新知 2026/2/6 15:01:23

排序算法总结（C++）

目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指：同样大小的样本 **（同样大小的数据）**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

编程新知 2026/2/10 5:05:24

基于SpringBoot在线拍卖系统的设计和实现

摘 要 随着社会的发展，社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统，主要的模块包括管理员；首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

编程新知 2026/1/26 13:25:02

【无标题】路径问题的革命性重构：基于二维拓扑收缩色动力学模型的零点隧穿理论

路径问题的革命性重构：基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中（图1）： mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

编程新知 2025/10/21 1:07:59