Matlab:解非线性方程组
1、基于问题求解非线性方程组
例:
x=optimvar('x',2); %将x定义为一个二元素优化变量
eq1=exp(-exp(-(x(1)+x(2))))==x(2)*(1+x(1)^2); %创建第一个方程作为优化等式表达式
eq2=x(1)*cos(x(2))+x(2)*sin(x(1))==1/2; %创建第二个方程作为优化等式表达式
prob=eqnproblem; %创建一个方程问题
prob.Equations.eq1=eq1;
prob.Equations.eq2=eq2; %将方程放入问题中
show(prob) %检查问题
x0.x=[0 0]; %从[0,0]点开始求解问题
[sol,fval,exitflag]=solve(prob,x0)
disp(sol.x) %查看解点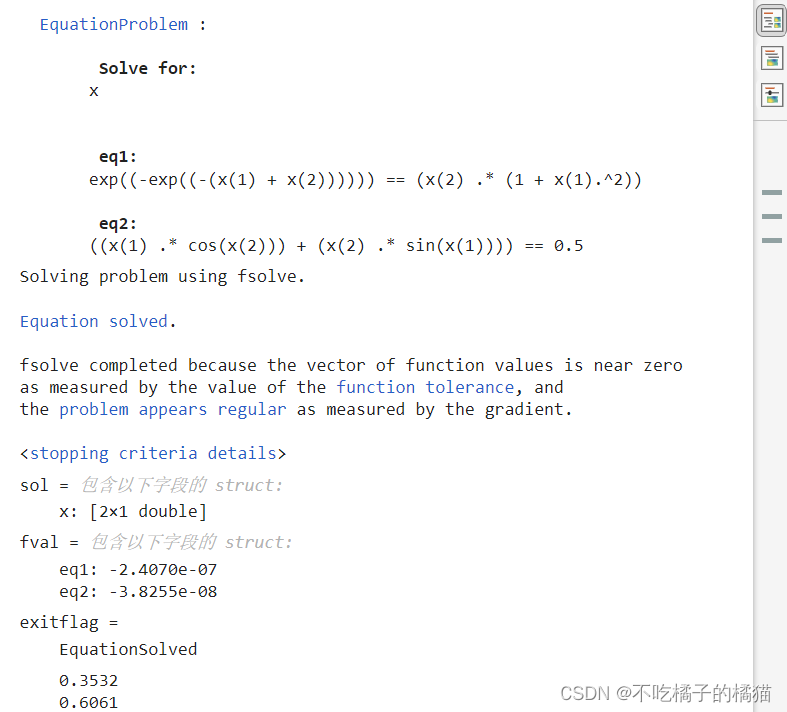 2、基于问题求解多项式非线性方程组
2、基于问题求解多项式非线性方程组
例:
已知x是2x2的矩阵,求解
x=optimvar('x',2,2); %将变量x定义为一个2×2矩阵变量
eqn=x^3 == [1,2;3,4]; %用x定义要求解的方程
prob=eqnproblem('Equations',eqn); %用方程创建一个问题
x0.x=ones(2); %从[1,1;1,1]点开始求解问题
sol=solve(prob,x0)
disp(sol.x) %检查解
sol.x^3 %显示解的立方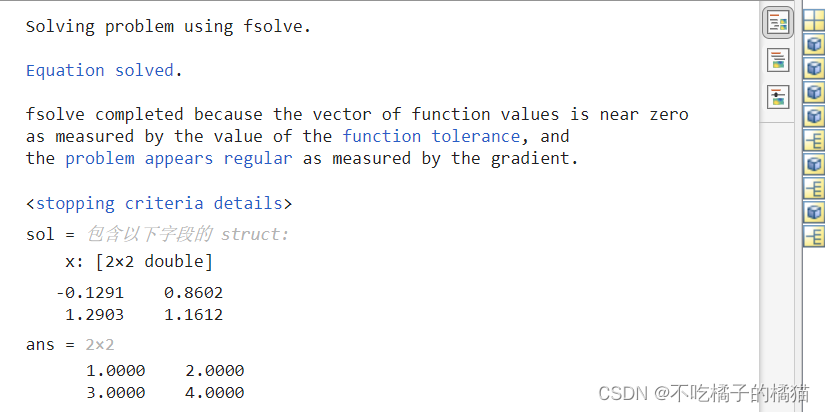
3、fsolve解非线性方程组
语法:
x = fsolve(fun,x0) %从x0 开始,尝试求解方程fun(x)=0(全零数组)
x = fsolve(fun,x0,options)
x = fsolve(problem)
[x,fval] = fsolve(___)
[x,fval,exitflag,output] = fsolve(___)
[x,fval,exitflag,output,jacobian] = fsolve(___)例:求解下面两个非线性方程组
(1)先将其转化成的形式
(2)创建root2d.m
function F = root2d(x)F(1) = exp(-exp(-(x(1)+x(2)))) - x(2)*(1+x(1)^2);
F(2) = x(1)*cos(x(2)) + x(2)*sin(x(1)) - 0.5;(3)
type root2d.m
fun=@root2d;
x0=[0,0];
x=fsolve(fun,x0)
4、迭代输出,展示方程组的求解过程
例:
(1)先将其转化成的形式
(2)
F=@(x)[2*x(1)-x(2)-exp(-x(1));-x(1)+2*x(2)-exp(-x(2))]; %编写一个函数用来算F
x0=[-5;-5]; %创建初始点x0[-5;-5]
options=optimoptions('fsolve','Display','iter'); %返回迭代输出
[x,fval]=fsolve(F,x0,options) %求解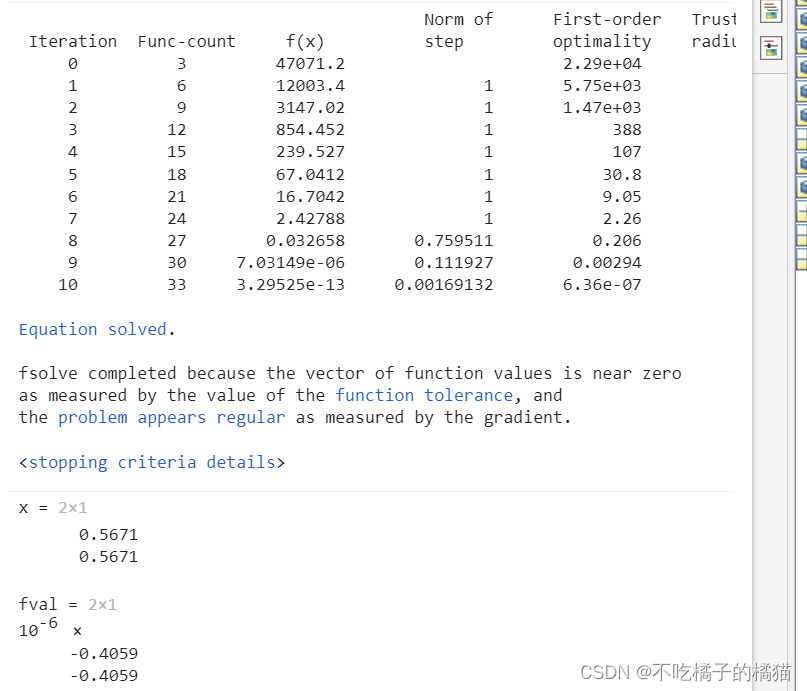
上接非线性https://blog.csdn.net/weixin_73011353/article/details/135141433![]() https://blog.csdn.net/weixin_73011353/article/details/135141433
https://blog.csdn.net/weixin_73011353/article/details/135141433
相关文章:
Matlab:解非线性方程组
1、基于问题求解非线性方程组 例: xoptimvar(x,2); %将x定义为一个二元素优化变量 eq1exp(-exp(-(x(1)x(2))))x(2)*(1x(1)^2); %创建第一个方程作为优化等式表达式 eq2x(1)*cos(x(2))x(2)*sin(x(1))1/2; %创建第二个方程作为优化等式表达式 probe…...

面向 AI,重塑云基础设施、存储、芯片、Serverless……2023亚马逊云科技re:Invent中国行
一年一度亚马逊云科技重要的技术盛会 re:Invent 刚落下帷幕,2023 亚马逊云科技 re:Invent 中国行就将其中重要的信息与内容带给了中国市场和用户。作为全球的云计算巨头,今年亚马逊云科技可以说全面加码 AI,例如发布完整的端到端生成式 AI 技…...

【JDK新特性】JDK和Springboot各版本新特性介绍
目录 参考资料 以下是一些较新版本的JDK的主要新特性介绍: JDK 8: Lambda 表达式:引入了函数式编程的概念,使得代码更简洁、可读性更强。Stream API:提供了一种高效处理集合数据的方式,支持并行处理。默认…...

tomcat剖析:开篇
一、简介 本专栏为解析tomcat的专栏,用于一步步的从构建到执行,再到剖析tomcat的内部构造,然后再加上自己的理解,从0到1去认识我们日常开发中不可或缺的web容器,希望对之后的软件设计能够有所启示。 二、步骤 2.1构…...
华为路由器:DHCP配置
在大型企业网络中,会有大量的主机获取IP地址等网络参数。如果采用手工配置,则工作量大不好管理,若用户擅自更改网络参数,则容易导致IP冲突。 因此使用动态主机配置协议(DHCP)可以减少管理员的工作量&#x…...

(企业 / 公司项目)微服务OpenFeign怎么实现服务间调用?(含面试题)
Feign: 远程调用组件使用步骤,理解上面的图 后台系统中, 微服务和微服务之间的调用可以通过Feign组件来完成. Feign组件集成了Ribbon负载均衡策略(默认开启的, 使用轮询机制),Hystrix熔断器 (默认关闭的, 需要通过配置文件进行设置开启) 被调用的微服务…...

数据结构:图文详解 树与二叉树(树与二叉树的概念和性质,存储,遍历)
目录 一.树的概念 二.树中重要的概念 三.二叉树的概念 满二叉树 完全二叉树 四.二叉树的性质 五.二叉树的存储 六.二叉树的遍历 前序遍历 中序遍历 后序遍历 一.树的概念 树是一种非线性数据结构,它由节点和边组成。树的每个节点可以有零个或多个子节点…...
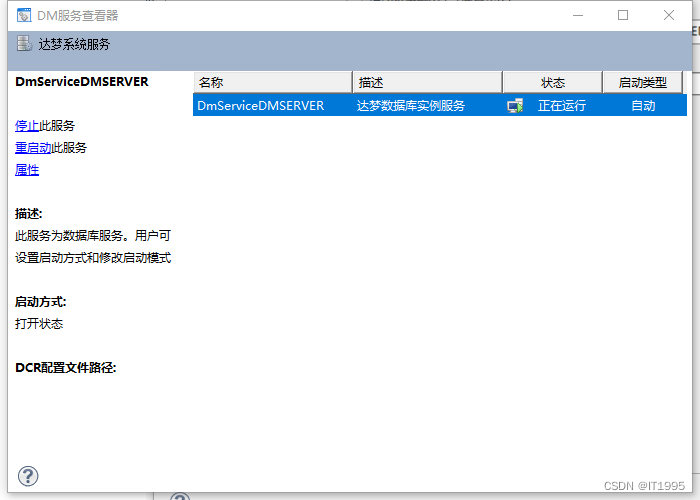
DM工作笔记-在windows下对DM7进行库还原恢复
提供了这些备份数据 在windows平台上,将这些备份数据还原到新库中。 首先实例得先停掉: 使用的软件console.exe: 重要步骤:①获取备份;②还原;③恢复 记住DMAP方式这个不要勾选,然后再获取备份…...

STM32软硬件CRC测速对比
硬件CRC配置 以及软硬件CRC速度对比 使用CUBEMX配置默认使用的是CRC32,从库中可以看出这一点 HAL库提供了以下两个计算函数 HAL_CRC_Accumulate(CRC_HandleTypeDef *hcrc, uint32_t pBuffer[], uint32_t BufferLength); 这个函数用于在已有的CRC校验结果的基础上累积…...
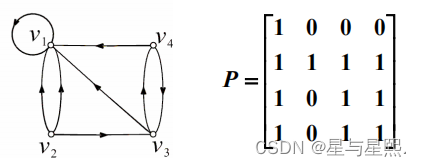
第九部分 图论
目录 例 相关概念 握手定理 例1 图的度数列 例 无向图的连通性 无向图的连通度 例2 例3 有向图D如图所示,求 A, A2, A3, A4,并回答诸问题: 中间有几章这里没有写,感兴趣可以自己去学,组合数学跟高中差不多,…...

如何用java实现对java虚拟机的性能监控?
要使用Java实现对Java虚拟机(JVM)的性能监控,可以使用Java Management Extensions(JMX)来获取和监控JVM的各种指标。以下是一个简单的示例代码,演示如何使用JMX监控JVM的内存使用情况: import …...
电路设计(7)——窗口比较器的multism仿真
1.功能设计 构建一个窗口比较器的电路,在输入电压大于3.5v,小于0.8v时,蜂鸣器报警,输入电压在0.8v到3.5v之间时,不报警。 整体电路如下: 2.设计思路 在输入端,采取电阻分压的方式,输…...

前端已死?探讨人工智能与低代码对前端的影响
文章目录 每日一句正能量前言前端行业究竟是好是坏?数字化转型的当下前端工程师该何去何从? 想要入行前端先认清这三个事实 后记 每日一句正能量 人的结构就是相互支撑,众人的事业需要每个人的参与。 前言 随着人工智能和低代码的崛起&#…...

树莓派,opencv,Picamera2利用舵机云台追踪人脸(PID控制)
一、需要准备的硬件 Raspiberry Pi 4b两个SG90 180度舵机(注意舵机的角度,最好是180度且带限位的,切勿选360度舵机)二自由度舵机云台(如下图)Raspiberry CSI 摄像头 组装后的效果: 二、项目目…...

uniapp中推出当前微信小程序
uni.exitMiniProgram() 通过代码直接退出当前小程序 uni.exitMiniProgram({success: function() {console.log(退出小程序成功);},fail: function(err) {console.log(退出小程序失败, err);} })...

AndroidStudio无法新建aidl文件解决办法
我用的 AS 版本是 Android Studio Giraffe | 2022.3.1 Build #AI-223.8836.35.2231.10406996, built on June 29, 2023 右键新建 aidl 文件, 提示 (AIDL File)Requires setting the buildFeatures.aidl to true in the build file 解决办法 修改 app 的 build.…...

java爬虫(jsoup)如何设置HTTP代理ip爬数据
目录 前言 什么是HTTP代理IP 使用Jsoup设置HTTP代理IP的步骤 1. 导入Jsoup依赖 2. 创建HttpProxy类 3. 设置代理服务器 4. 使用Jsoup进行爬取 结论 前言 在Java中使用Jsoup进行网络爬虫操作时,有时需要使用HTTP代理IP来爬取数据。本文将介绍如何使用Jsoup设…...

ZooKeeper Client API 安装及使用指北
下载 wget https://archive.apache.org/dist/zookeeper/zookeeper-3.5.4-beta/zookeeper-3.5.4-beta.tar.gz解压 tar -zxf zookeeper-3.5.4-beta.tar.gz安装 cd zookeeper-3.5.4-beta/src/c/ ./configure make sudo make install到 make 这一步大概率会出现报错:…...
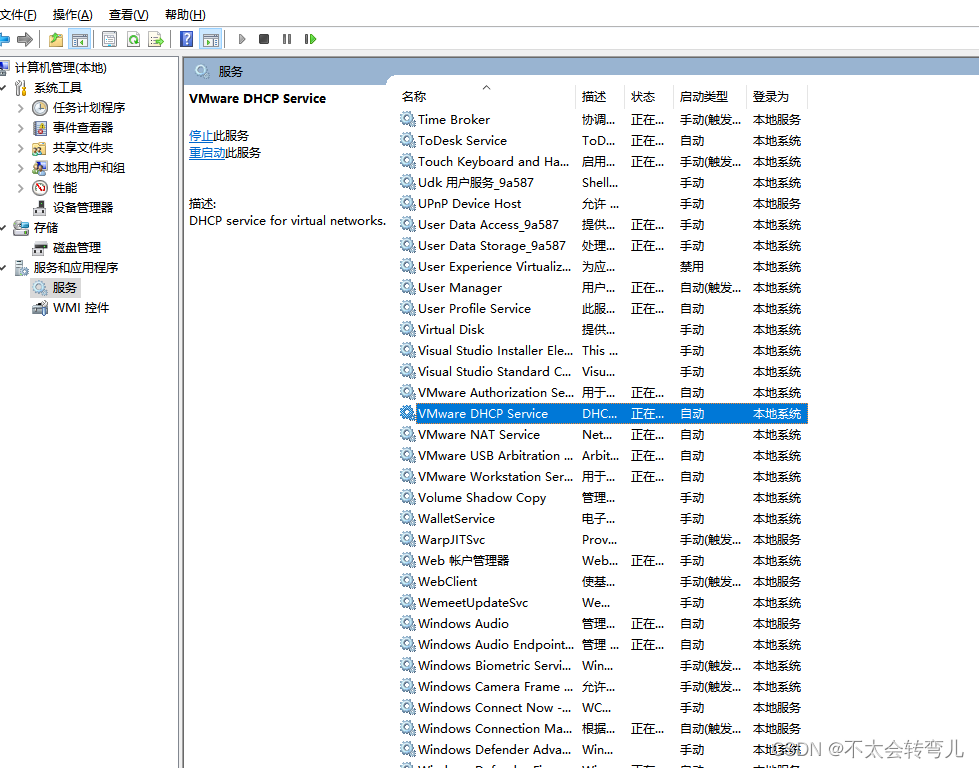
本机ping不通虚拟机
windows下finall shell连不上虚拟机了,之前是可以的,然后ping虚拟机,发现也ping不通,随后到处找问题。 在本地部分,控制面板 ——>网络和Internet——>网络连接 , 可以看到 VMnet1和Vmnet8虽然都是已…...

Linux cfdisk命令
Linux cfdisk命令用于磁盘分区。 cfdisk是用来磁盘分区的程序,它十分类似DOS的fdisk,具有互动式操作界面而非传统fdisk的问答式界面,您可以轻易地利用方向键来操控分区操作。 语法 cfdisk [-avz][-c <柱面数目>-h <磁头数目>-…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...
