数据结构-十大排序算法
数据结构十大排序算法
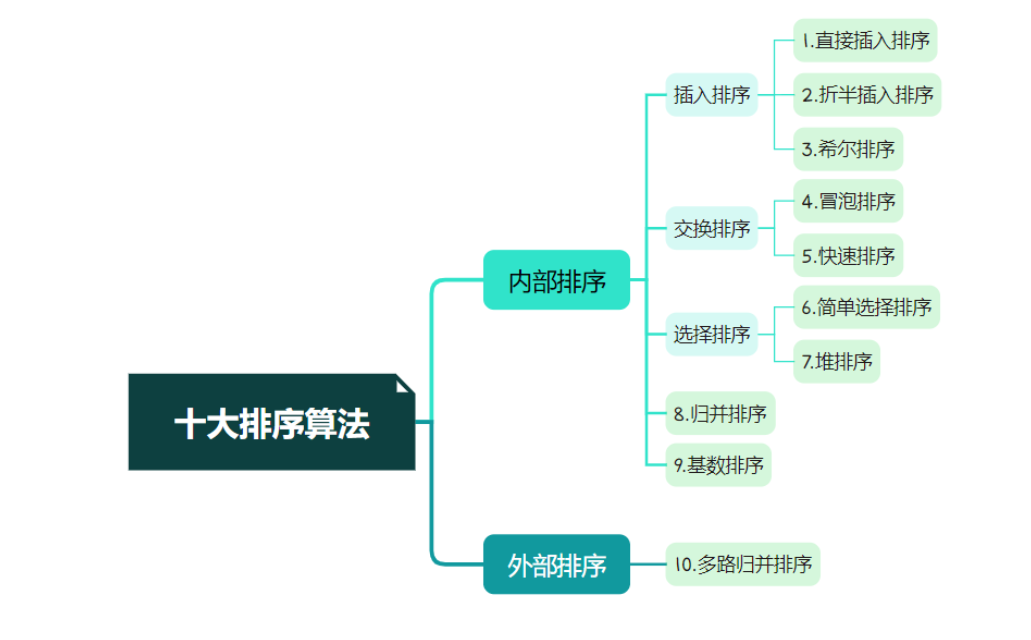
十大排序算法分别是直接插入排序、折半插入排序、希尔排序、冒泡排序、快速排序、简单选择排序、堆排序、归并排序、基数排序、外部排序。
其中插入排序包括直接插入排序、折半插入排序、希尔排序;交换排序包括冒泡排序、快速排序;选择排序包括简单选择排序、堆排序
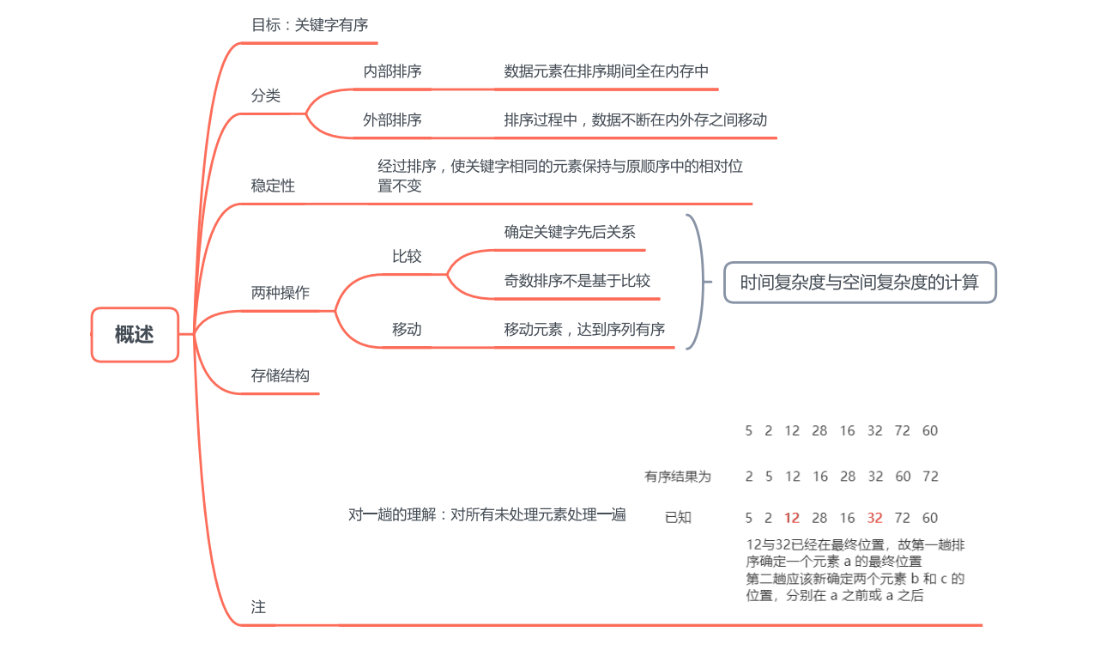
1. 直接插入排序
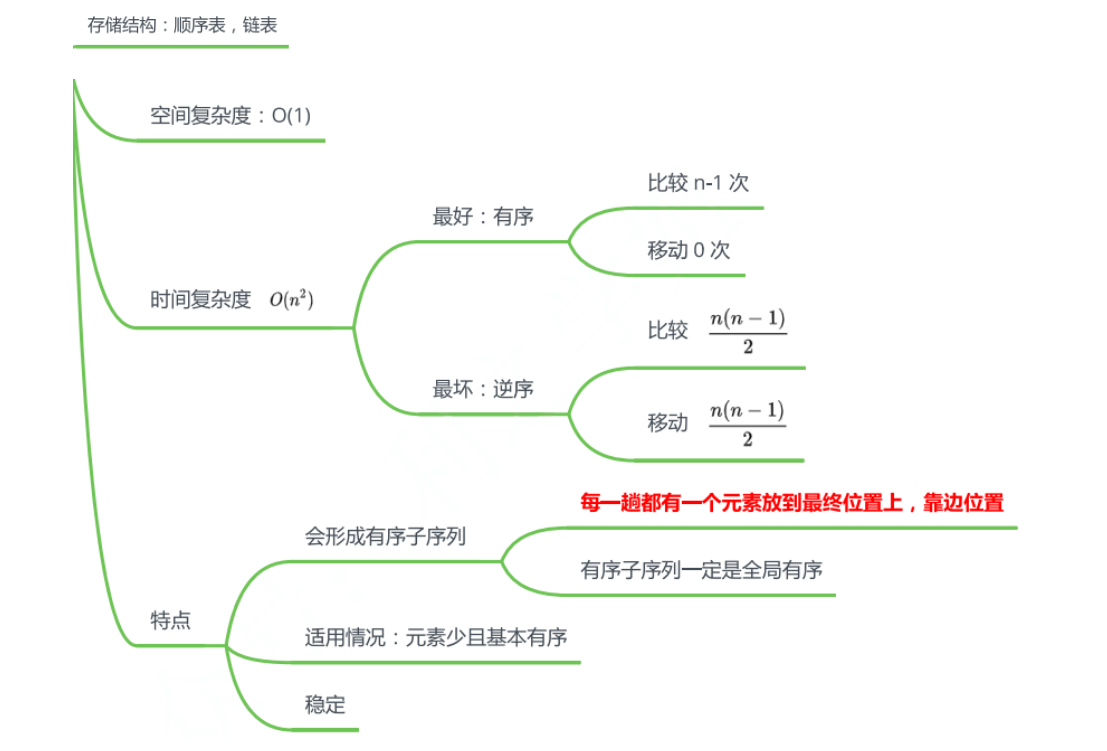
直接插入排序(Insertion Sort)是一种简单的排序算法,它的基本思想是将待排序的元素逐个插入已经有序的部分序列中,从而得到一个有序的序列。
下面是直接插入排序的步骤:
- 假设要对一个数组进行升序排序,从第二个元素开始,将其作为当前元素。
- 将当前元素与已排序的部分序列进行比较,找到合适的位置插入当前元素。如果当前元素小于已排序部分的某个元素,就将这个元素后移一位,直到找到合适的位置。
- 将当前元素插入到合适的位置。
- 重复步骤 2 和步骤 3,直到所有元素都被插入到合适的位置。
以下是使用 C 实现的直接插入排序的示例代码:

void insertionSort(int arr[], int n) {int i, j, current;for (i = 1; i < n; i++) {current = arr[i];j = i - 1;while (j >= 0 && arr[j] > current) {arr[j + 1] = arr[j];j--;}arr[j + 1] = current;}
}
2.折半插入排序
折半插入排序(Binary Insertion Sort)是对直接插入排序算法的改进,通过利用二分查找的方式来寻找插入位置,减少了比较的次数,从而提高了排序的效率。
下面是折半插入排序的步骤:
- 假设要对一个数组进行升序排序,从第二个元素开始,将其作为当前元素。
- 将当前元素与已排序的部分序列的中间元素进行比较,确定插入位置的范围。
- 使用二分查找在确定的范围内找到合适的位置插入当前元素。
- 将当前元素插入到合适的位置。
- 重复步骤 2 到步骤 4,直到所有元素都被插入到合适的位置。
以下是使用 C 语言实现折半插入排序的示例代码:
void binaryInsertionSort(int arr[], int n) {int i, j, current, low, high, mid;for (i = 1; i < n; i++) {current = arr[i];low = 0;high = i - 1;// 使用二分查找确定插入位置的范围while (low <= high) {mid = (low + high) / 2;if (arr[mid] > current)high = mid - 1;elselow = mid + 1;}// 插入当前元素到合适的位置for (j = i - 1; j >= low; j--) {arr[j + 1] = arr[j];}arr[low] = current;}
}
3.希尔排序
希尔排序(Shell Sort)是一种改进的插入排序算法,它通过比较和交换相隔一定间隔的元素,逐步减小间隔,最终使整个序列达到有序状态。
下面是希尔排序的步骤:
- 首先选择一个间隔序列(增量序列),通常使用 Knuth 序列或者 Hibbard 序列。这些序列中的元素逐步减小,最后一个元素为 1。
- 对于每个间隔,将数组分为多个子序列,分别对这些子序列进行插入排序。
- 逐步减小间隔,重复步骤 2,直到间隔为 1。
- 最后进行一次间隔为 1 的插入排序,完成整个排序过程。
以下是使用 C 语言实现希尔排序的示例代码:


#include <stdio.h>void shellSort(int arr[], int n) {int gap, i, j, temp;// 使用 Knuth 序列计算初始间隔gap = 1;while (gap < n / 3) {gap = gap * 3 + 1;}while (gap > 0) {for (i = gap; i < n; i++) {temp = arr[i];j = i;while (j > gap - 1 && arr[j - gap] > temp) {arr[j] = arr[j - gap];j -= gap;}arr[j] = temp;}// 缩小间隔gap = (gap - 1) / 3;}
}// 示例用法
int main() {int arr[] = {5, 2, 8, 1, 3};int n = sizeof(arr) / sizeof(arr[0]);shellSort(arr, n);printf("Sorted array: ");for (int i = 0; i < n; i++) {printf("%d ", arr[i]);}printf("\n");return 0;
}4.冒泡排序
冒泡排序(Bubble Sort)是一种简单的排序算法,它重复地比较相邻的两个元素,并交换顺序不正确的元素,直到整个序列排序完成。
下面是冒泡排序的步骤:
- 从序列的第一个元素开始,比较该元素与下一个元素的大小。
- 如果当前元素大于下一个元素,则交换它们的位置。
- 继续向后比较相邻的元素,重复步骤 2,直到遍历到倒数第二个元素。
- 重复步骤 1 到步骤 3,直到没有需要交换的元素,即序列已经排序完成。
以下是使用 C 语言实现冒泡排序的示例代码:

void bubbleSort(int arr[], int n) {int i, j, temp;for (i = 0; i < n - 1; i++) {for (j = 0; j < n - i - 1; j++) {if (arr[j] > arr[j + 1]) {// 交换元素temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;}}}
}
5.快速排序
快速排序(Quick Sort)是一种高效的排序算法,它基于分治的思想,通过将数组分成较小的子数组,然后递归地对子数组进行排序,最终将整个数组排序。
以下是快速排序的步骤:
- 选择一个元素作为基准(通常选择数组的第一个元素)。
- 将数组分成两个子数组,比基准小的元素放在左边,比基准大的元素放在右边。
- 对左右两个子数组递归地执行步骤 1 和步骤 2,直到子数组的长度为 0 或 1,表示已经排序完成。
- 合并排序后的子数组,得到最终的排序结果。
以下是使用 C 语言实现快速排序的示例代码:



// 交换两个元素的值
void swap(int* a, int* b) {int temp = *a;*a = *b;*b = temp;
}// 将数组分成左右两个子数组,并返回基准元素的最终位置
int partition(int arr[], int low, int high) {int pivot = arr[low]; // 选择第一个元素作为基准int i = low + 1;int j = high;while (1) {// 在左侧找到第一个大于基准的元素的位置while (i <= j && arr[i] < pivot) {i++;}// 在右侧找到第一个小于基准的元素的位置while (j >= i && arr[j] > pivot) {j--;}// 若两个指针相遇或交错,则跳出循环if (i >= j) {break;}// 交换元素,使小于基准的元素在左侧,大于基准的元素在右侧swap(&arr[i], &arr[j]);i++;j--;}// 将基准元素放到最终的位置swap(&arr[low], &arr[j]);// 返回基准元素的位置return j;
}// 执行快速排序算法
void quickSort(int arr[], int low, int high) {if (low < high) {// 划分子数组,并获取基准元素的位置int pivotIndex = partition(arr, low, high);// 对左侧子数组进行快速排序quickSort(arr, low, pivotIndex - 1);// 对右侧子数组进行快速排序quickSort(arr, pivotIndex + 1, high);}
}
6.简单选择排序
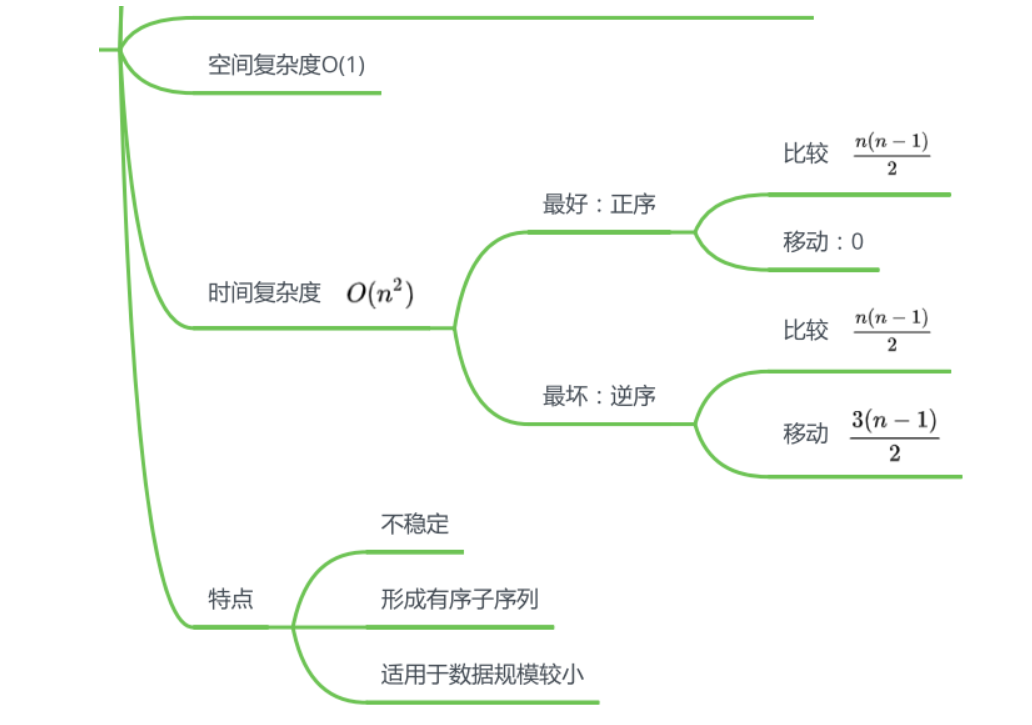
简单选择排序(Selection Sort)是一种简单直观的排序算法,它每次从未排序的部分选择最小(或最大)的元素,并将其放到已排序部分的末尾。
以下是简单选择排序的步骤:
- 在未排序部分中,找到最小(或最大)的元素。
- 将最小(或最大)的元素与未排序部分的第一个元素交换位置。
- 将已排序部分的末尾向后扩展一个位置。
- 重复步骤 1 到步骤 3,直到未排序部分为空。
以下是使用 C 语言实现简单选择排序的示例代码:

void swap(int* a, int* b) {int temp = *a;*a = *b;*b = temp;
}void selectionSort(int arr[], int n) {int i, j, minIndex;for (i = 0; i < n - 1; i++) {minIndex = i;for (j = i + 1; j < n; j++) {if (arr[j] < arr[minIndex]) {minIndex = j;}}swap(&arr[i], &arr[minIndex]);}
}7.堆排序
堆排序(Heap Sort)是一种基于堆数据结构的排序算法,它利用堆的性质进行排序。堆排序分为两个步骤:建堆和排序。
以下是堆排序的步骤:
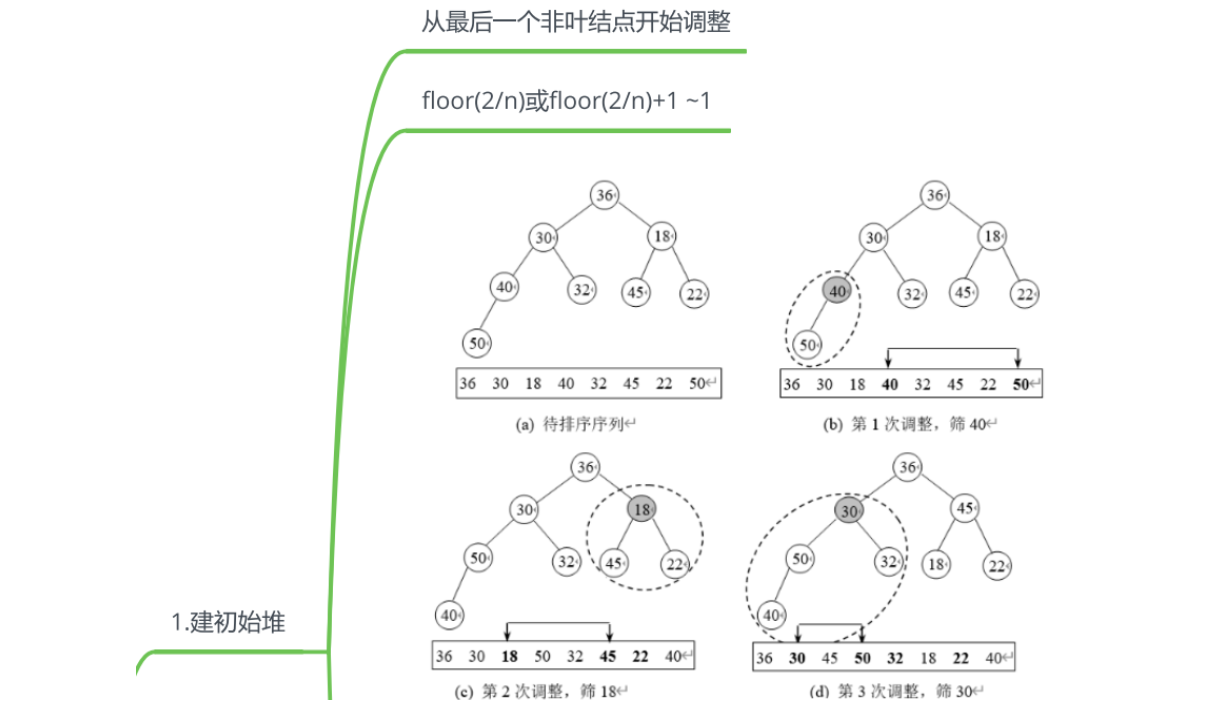
- 建堆(Heapify):将待排序的数组构建成一个堆结构。堆是一个完全二叉树,其中每个节点的值都大于等于(或小于等于)其子节点的值,这被称为最大堆(或最小堆)的性质。
- 排序:将堆顶元素与最后一个叶节点交换,并从根节点开始调整堆,使其满足堆的性质。然后再次将堆顶元素与倒数第二个叶节点交换,再次调整堆。重复这个过程,直到堆中剩下一个元素为止。
以下是使用 C 语言实现堆排序的示例代码:


// 交换两个元素的值
void swap(int* a, int* b) {int temp = *a;*a = *b;*b = temp;
}// 对以rootIndex为根节点的子树进行堆调整,n为堆的大小
void heapify(int arr[], int n, int rootIndex) {int largest = rootIndex; // 最大元素的索引int leftChild = 2 * rootIndex + 1; // 左子节点的索引int rightChild = 2 * rootIndex + 2; // 右子节点的索引// 找出左右子节点和根节点中的最大元素if (leftChild < n && arr[leftChild] > arr[largest]) {largest = leftChild;}if (rightChild < n && arr[rightChild] > arr[largest]) {largest = rightChild;}// 如果最大元素不是根节点,则交换根节点和最大元素,并递归调整交换后的子树if (largest != rootIndex) {swap(&arr[rootIndex], &arr[largest]);heapify(arr, n, largest);}
}// 堆排序
void heapSort(int arr[], int n) {// 构建最大堆,从最后一个非叶节点开始向上调整for (int i = n / 2 - 1; i >= 0; i--) {heapify(arr, n, i);}// 依次将堆顶元素与末尾元素交换,并重新调整堆for (int i = n - 1; i >= 0; i--) {swap(&arr[0], &arr[i]);heapify(arr, i, 0);}
}在上述代码中,我们定义了一个辅助函数 swap,用于交换两个元素的值。
然后,我们定义了 heapify 函数来进行堆调整,以满足堆的性质。
接下来,我们定义了 heapSort 函数来执行堆排序算法。在该函数中,我们首先构建一个最大堆,然后依次将堆顶元素与末尾元素交换,并重新调整堆。
8.归并排序
归并排序(Merge Sort)是一种基于分治思想的排序算法。它将待排序的数组分成两个子数组,分别进行排序,然后将排序后的子数组合并成一个有序数组。归并排序的关键步骤是合并(Merge)操作,通过将两个有序的子数组合并成一个有序数组来实现排序。
以下是归并排序的步骤:
- 分解:将待排序的数组递归地分解成两个子数组,直到每个子数组只剩下一个元素或为空。
- 合并:将两个有序的子数组合并成一个有序数组。合并过程中,依次比较两个子数组的元素,将较小(或较大)的元素放入临时数组中,并更新索引,直到其中一个子数组的所有元素都放入临时数组中。将剩余的元素依次放入临时数组中。
- 返回合并后的有序数组。
以下是使用 C 语言实现归并排序的示例代码:


#include <stdio.h>
#include <stdlib.h>// 合并两个有序子数组为一个有序数组
void merge(int arr[], int left, int mid, int right) {int n1 = mid - left + 1; // 左子数组的元素个数int n2 = right - mid; // 右子数组的元素个数// 创建临时数组来存储两个子数组的元素int* leftArr = (int*)malloc(n1 * sizeof(int));int* rightArr = (int*)malloc(n2 * sizeof(int));// 将元素复制到临时数组中for (int i = 0; i < n1; i++) {leftArr[i] = arr[left + i];}for (int j = 0; j < n2; j++) {rightArr[j] = arr[mid + 1 + j];}// 合并两个子数组为一个有序数组int i = 0; // 左子数组的索引int j = 0; // 右子数组的索引int k = left; // 合并后数组的索引while (i < n1 && j < n2) {if (leftArr[i] <= rightArr[j]) {arr[k] = leftArr[i];i++;} else {arr[k] = rightArr[j];j++;}k++;}// 将剩余的元素放入合并后的数组中while (i < n1) {arr[k] = leftArr[i];i++;k++;}while (j < n2) {arr[k] = rightArr[j];j++;k++;}// 释放临时数组的内存free(leftArr);free(rightArr);
}// 归并排序递归函数
void mergeSort(int arr[], int left, int right) {if (left < right) {int mid = left + (right - left) / 2; // 计算中间索引// 递归地对左右子数组进行排序mergeSort(arr, left, mid);mergeSort(arr, mid + 1, right);// 合并两个有序子数组merge(arr, left, mid, right);}
}// 示例用法
int main() {int arr[] = {5, 2, 8, 1, 3};int n = sizeof(arr) / sizeof(arr[0]);mergeSort(arr, 0, n - 1);printf("Sorted array: ");for (int i = 0; i < n; i++) {printf("%d ", arr[i]);}printf("\n");return 0;
}在上述代码中,我们定义了 merge 函数,用于合并两个有序子数组。该函数接受数组 arr、左子数组的起始索引 left、中间索引 mid 和右子数组的结束索引 right。
然后,我们定义了 mergeSort 函数来执行归并排序算法。该函数采用分治的思想,首先递归地对左右子数组进行排序,然后调用 merge 函数合并两个有序子数组。
9.基数排序
基数排序(Radix Sort)是一种非比较型的排序算法,它根据元素的位数进行排序。基数排序逐位比较元素,从最低有效位(LSB)到最高有效位(MSB)进行排序。在每一位上,使用稳定的排序算法(如计数排序或桶排序)对元素进行排序。通过重复这个过程,直到对所有位都完成排序,最终得到一个有序的数组。
以下是基数排序的步骤:
- 获取数组中最大元素的位数(最大元素的位数决定了排序的轮数)。
- 对每一位进行排序:
- 使用稳定的排序算法对当前位进行排序(例如计数排序或桶排序)。
- 根据当前位的值将元素放入对应的桶中。
- 将桶中的元素按照顺序取出,更新原数组。
- 重复步骤 2 直到对所有位都完成排序。
以下是使用 C 语言实现基数排序的示例代码,使用计数排序作为稳定的排序算法:
#include <stdio.h>// 获取数组中的最大元素
int getMax(int arr[], int n) {int max = arr[0];for (int i = 1; i < n; i++) {if (arr[i] > max) {max = arr[i];}}return max;
}// 使用计数排序对数组按照指定的位进行排序
void countSort(int arr[], int n, int exp) {const int MAX_RANGE = 10; // 桶的范围,0-9int output[n]; // 存储排序结果的临时数组int count[MAX_RANGE] = {0};// 统计当前位上每个数字的出现次数for (int i = 0; i < n; i++) {count[(arr[i] / exp) % 10]++;}// 计算每个数字在排序后的数组中的起始索引for (int i = 1; i < MAX_RANGE; i++) {count[i] += count[i - 1];}// 将元素按照当前位的值放入临时数组中,同时更新 count 数组for (int i = n - 1; i >= 0; i--) {output[count[(arr[i] / exp) % 10] - 1] = arr[i];count[(arr[i] / exp) % 10]--;}// 将临时数组的元素复制回原数组for (int i = 0; i < n; i++) {arr[i] = output[i];}
}// 基数排序
void radixSort(int arr[], int n) {int max = getMax(arr, n); // 获取最大元素// 对每一位进行排序for (int exp = 1; max / exp > 0; exp *= 10) {countSort(arr, n, exp);}
}在上述代码中,我们定义了 getMax 函数,用于获取数组中的最大元素。
然后,我们定义了 countSort 函数,用于对数组按照指定的位进行排序。该函数采用计数排序算法,在每一位上统计元素的出现次数,然后根据当前位的值将元素放入对应的桶中,并更新原数组。
接下来,我们定义了 radixSort 函数来执行基数排序算法。该函数通过循环对每一位进行排序,调用 countSort 函数。
10.外部排序
外部排序(External Sorting)是一种用于处理大规模数据的排序算法,其中数据量大于计算机内存的容量。外部排序通常涉及将数据分割成较小的块,然后在内存中对这些块进行排序,并最终将它们合并为一个有序的结果。
以下是一种常见的外部排序算法:多路归并排序(Multiway Merge Sort)。
多路归并排序的基本思想是将大型数据集分割成更小的块(通常是内存可容纳的大小),在内存中对这些块进行排序,然后使用归并操作将它们合并成一个有序的结果。
以下是多路归并排序的步骤:
- 将大型数据集划分为较小的块,每个块可以适应内存容量。可以使用外部缓存或者分割文件为固定大小的块来实现。
- 将每个块加载到内存中,并使用内部排序算法(如快速排序、归并排序等)对块进行排序。
- 创建一个输出文件作为最终的有序结果。
- 从每个块中读取一部分数据到内存中(通常是一个块的大小),选择最小的元素,将其写入输出文件。
- 如果块中的数据被消耗完,从该块所在的文件中读取下一块数据到内存中。
- 重复步骤 4 和步骤 5,直到所有块中的数据都被处理。
- 关闭输出文件,排序完成。
需要注意的是,多路归并排序需要使用外部存储器(例如磁盘)来存储和处理大量数据,因此算法的性能会受到外部存储器的读写速度的限制。
实际的外部排序算法中,还会考虑更复杂的策略,如缓冲区管理、归并策略等,以提高排序的效率和性能。
外部排序是一种常用的处理大规模数据的排序方法,在处理海量数据、大型数据库等场景中有广泛的应用。



相关文章:

数据结构-十大排序算法
数据结构十大排序算法 十大排序算法分别是直接插入排序、折半插入排序、希尔排序、冒泡排序、快速排序、简单选择排序、堆排序、归并排序、基数排序、外部排序。 其中插入排序包括直接插入排序、折半插入排序、希尔排序;交换排序包括冒泡排序、快速排序࿱…...
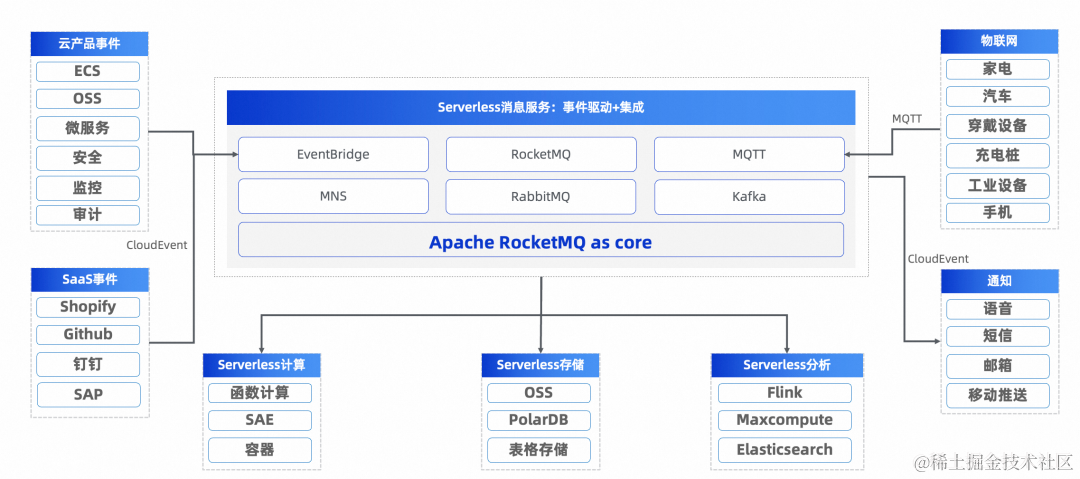
Apache RocketMQ,构建云原生统一消息引擎
本文整理于 2023 年云栖大会林清山带来的主题演讲《Apache RocketMQ 云原生统一消息引擎》 演讲嘉宾: 林清山(花名:隆基),Apache RocketMQ 联合创始人,阿里云资深技术专家,阿里云消息产品线负…...
 ClickHouse 中使用 `MaterializedMySQL` 引擎单独同步 MySQL 数据库中的特定表(例如 `aaa` 和 `bbb`))
(四) ClickHouse 中使用 `MaterializedMySQL` 引擎单独同步 MySQL 数据库中的特定表(例如 `aaa` 和 `bbb`)
要在 ClickHouse 中使用 MaterializedMySQL 引擎单独同步 MySQL 数据库中的特定表(例如 aaa 和 bbb),您可以使用 TABLE OVERRIDE 功能。这个功能允许您指定要同步的特定表,同时忽略其他表。以下是步骤说明: 1. 启用 M…...

TikTok真题第4天 | 1366. 通过投票对团队排名、1029.两地调度、562.矩阵中最长的连续1线段
1366. 通过投票对团队排名 题目链接:rank-teams-by-votes/ 解法: 这道题就是统计每个队伍在每个排名的投票数,队伍为A、B、C,则排名有1、2、3,按照投票数进行降序排列。如果有队伍在每个排名的投票数都一样…...

时序预测 | Matlab实现SSA-CNN-LSTM麻雀算法优化卷积长短期记忆神经网络时间序列预测
时序预测 | Matlab实现SSA-CNN-LSTM麻雀算法优化卷积长短期记忆神经网络时间序列预测 目录 时序预测 | Matlab实现SSA-CNN-LSTM麻雀算法优化卷积长短期记忆神经网络时间序列预测预测效果基本介绍程序设计参考资料 预测效果 基本介绍 MATLAB实现SSA-CNN-LSTM麻雀算法优化卷积长短…...
负载均衡——Ribbon
文章目录 Ribbon和Eureka配合使用项目引入RibbonRestTemplate添加LoadBalanced注解注意自定义均衡方式代码注册方式配置方式 Ribbon脱离Eureka使用 Ribbon,Nexflix发布的负载均衡器,有助于控制HTTP和TCP客户端的行为。基于某种负载均衡算法(轮…...

7.微服务设计原则
1.微服务演进策略 从单体应用向微服务演进策略: 绞杀者策略,修缮者策略的另起炉灶策略; 绞杀者策赂 绞杀者策略是一种逐步剥离业务能力,用微服务逐步替代原有单体应用的策略。它对单体应用进行领域建模,根据领域边界࿰…...

【MATLAB库函数系列】线性调频Z(Chirp-Z,CZT)的MATLAB源码和C语言实现
在上一篇博客 【数字信号处理】线性调频Z(Chirp-Z,CZT)算法详解 已经详细介绍了CZT变换的应用背景和原理,先回顾一下: 回顾CZT算法 采用 FFT 算法可以很快计算出全部 N N N点 DFT 值,即Z变换 X ( z ) X(z) <...
BIT-6-指针(C语言初阶学习)
1. 指针是什么 2. 指针和指针类型 3. 野指针 4. 指针运算 5. 指针和数组 6. 二级指针 7. 指针数组 1. 指针是什么? 指针是什么? 指针理解的2个要点: 指针是内存中一个最小单元的编号,也就是地址平时口语中说的指针,通常…...
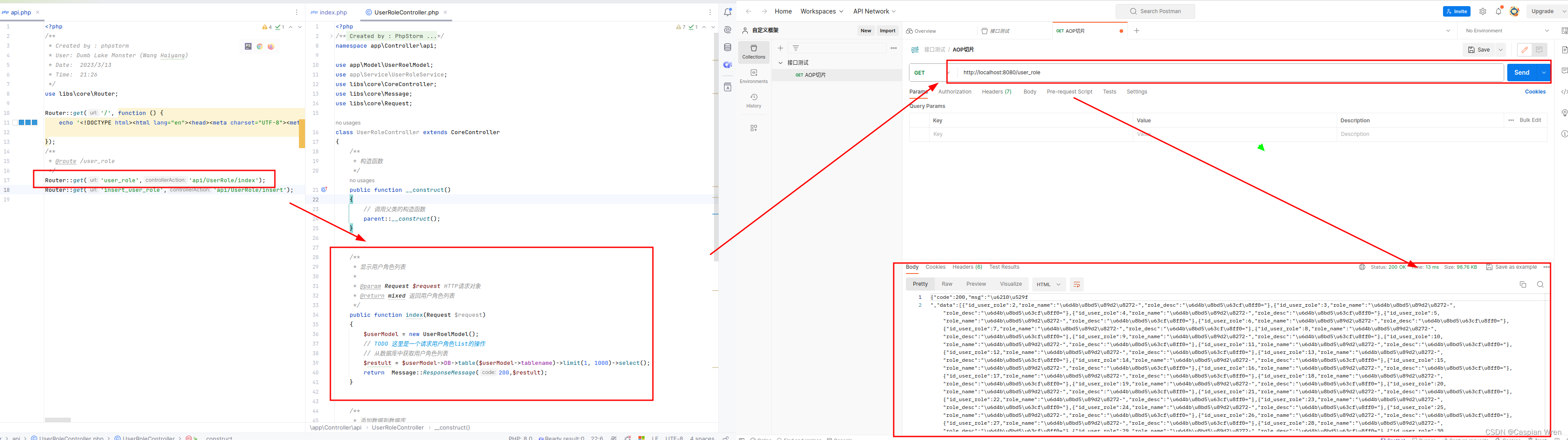
傻瓜式教学Docker 使用docker compose部署 php nginx mysql
首先你可以准备这个三个服务,也可以在docker compose 文件中 直接拉去指定镜像,这里演示的是镜像服务已经在本地安装好了,提供如下: PHP # 设置基础镜像 FROM php:8.2-fpm# install dependencies RUN apt-get update && apt-get install -y \vim \libzip-dev \libpng…...

node express简单微服务
首先,安装所需的依赖项,可以使用npm或yarn进行安装: $ npm install express axios接下来,创建一个名为service1.js的文件,用于实现第一个微服务: const express require(express); const axios require…...
nginx-proxy-manager初次登录502 bad gateway
nginx-proxy-manager初次登录502 bad gateway 按照官方docker-compose安装后,页面如下: 默认账户密码: adminexample.com/changeme点击sign in,提示Bad Gateway 打开调试 重装后依然如此,最后查阅githup issue 找到答案 https://github.com/NginxProxyManager/nginx-proxy-…...

Servlet见解2
4 创建servlet的三种方式 4.1 实现Servlet接口的方式 import javax.servlet.*; import javax.servlet.annotation.WebServlet; import java.io.IOException;WebServlet("/test1") public class Servlet1 implements Servlet {Overridepublic void init(ServletConf…...

【SpringCloud】-OpenFeign实战及源码解析、与Ribbon结合
一、背景介绍 二、正文 OpenFeign是什么? OpenFeign(简称Feign)是一个声明式的Web服务客户端,用于简化服务之间的HTTP通信。与Nacos和Ribbon等组件协同,以支持在微服务体系结构中方便地进行服务间的通信;…...

走进数字金融峰会,为金融科技数字化赋能
12月20—21日,FSIDigital数字金融峰会在上海圆满召开。本次峰会包含InsurDigital数字保险峰会和B&SDigital数字银行与证券峰会2场平行峰会;吸引了近600位来自保险、银行、证券以及金融科技等行业的领导者和专家齐聚一堂,共同探讨金融业数…...

docker-compose部署kafka
docker-compose.yml配置 version: "3" services:kafka:image: bitnami/kafka:latestports:- 7050:7050environment:- KAFKA_ENABLE_KRAFTyes- KAFKA_CFG_PROCESS_ROLESbroker,controller- KAFKA_CFG_CONTROLLER_LISTENER_NAMESCONTROLLER- KAFKA_CFG_LISTENERSPLAIN…...
Spark与Hadoop的关系和区别
在大数据领域,Spark和Hadoop是两个备受欢迎的分布式数据处理框架,它们在处理大规模数据时都具有重要作用。本文将深入探讨Spark与Hadoop之间的关系和区别,以帮助大家的功能和用途。 Spark和Hadoop简介 1 Hadoop Hadoop是一个由Apache基金会…...
蓝桥杯-Excel地址[Java]
目录: 学习目标: 学习内容: 学习时间: 题目: 题目描述: 输入描述: 输出描述: 输入输出样例: 示例 1: 运行限制: 题解: 思路: 学习目标: 刷蓝桥杯题库日记 学习内容: 编号96题目Ex…...

OSPF多区域配置-新版(12)
目录 整体拓扑 操作步骤 1.基本配置 1.1 配置R1的IP 1.2 配置R2的IP 1.3 配置R3的IP 1.4 配置R4的IP 1.5 配置R5的IP 1.6 配置R6的IP 1.7 配置PC-1的IP地址 1.8 配置PC-2的IP地址 1.9 配置PC-3的IP地址 1.10 配置PC-4的IP地址 1.11 检测R5与PC1连通性 1.12 检测…...
华为---USG6000V防火墙web基本配置示例
目录 1. 实验要求 2. 配置思路 3. 网络拓扑图 4. USG6000V防火墙端口和各终端相关配置 5. 在USG6000V防火墙web管理界面创建区域和添加相应端口 6. 给USG6000V防火墙端口配置IP地址 7. 配置通行策略 8. 测试验证 8.1 逐个删除策略,再看各区域终端通信情况 …...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...
