【宇宙猜想】AR文创入驻今日美术馆、北京天文馆等众多展馆,在AR互动中感受科技魅力!
近日,由「宇宙猜想」推出的AR系列文创产品先后入驻今日美术馆、北京天文馆、国家自然博物馆、上海天文馆、国家海洋馆、中华手工展馆等各大馆场并与其展开相关合作。

「宇宙猜想」致力于创造虚拟空间价值,用AR技术与文创产品碰撞出新的火花,为用户提供轻松触达元宇宙的全新体验。此次入驻众多展馆,更是「宇宙猜想」在推动科技与文化融合方面的一次重要尝试。

“AR+文创”,游一馆见天地之大
「宇宙猜想」以天体星球为灵感来源,创造了“星球探索”系列,将AR技术与天文知识相结合,为用户带来全新的互动体验。

“宇宙猜想”AR星球系列产品入驻《今日美术馆》
在“星球探索”系列中,每一个星球都是一个独立的世界,拥有独特的地质特征、气候环境和生态系统。
在“今日美术馆”中,我们通过「宇宙猜想App」扫描现场的AR星球模型,就可以近距离观察星球细节、了解天文知识、感受独特魅力,仿佛身临其境地置身于宇宙之中,从而激发我们对宇宙的好奇心和探索欲。

“宇宙猜想”文创产品入驻《漫无边界航天艺术展》
同时,「宇宙猜想」还利用城市数字孪生技术,1:1复刻了现实空间,打造一触即达的数字平行世界。我们可以在城市的各个场景中游玩探索,观察城市景象,打卡互动。
「宇宙猜想」的“星球探索”系列,不仅仅是一个科技产品,更是一次对未来世界的深度探索,让我们在探索宇宙的过程中,领略到天地之大。

数字云游山海历史,入一馆感受历史遗迹
在「宇宙猜想」的AR文创作品中,我们不仅可以领略到宇宙的浩瀚和神秘,还可以重现古代建筑文化的盛景与辉煌。
「宇宙猜想」AR文创作品通过前沿技术手段加持,将古代建筑“集贤亭”和历史文物“后母戊鼎”进行数字化重建,让我们能够在虚拟空间中欣赏到这些古朴建筑和文物的原始风貌及艺术价值。

“宇宙猜想”AR扫万物《集贤亭》
通过“AR扫万物”功能,我们不仅可以看到“集贤亭”和“后母戊鼎”的外观,还可以深入探索这些古代建筑的内部结构,观察它们的建筑细节和艺术价值,让我们能够更加深入地了解古代建筑的历史和文化内涵,感受古代工匠的精湛技艺和艺术创造力。

“宇宙猜想”AR扫万物《后母戊鼎》
除了古代建筑,「宇宙猜想」还致力于将更多历史遗迹进行数字化重建。在元宇宙空间中,我们可以观察到逼真的历史场景和文物遗迹,感受到古代文明的独特魅力。这种互动体验让我们能够更加深入地了解历史,探索人类文明的发展历程。

“宇宙猜想”文创产品入驻《中华手工展馆》
「宇宙猜想」作为国内虚实融合的数字化服务品牌,根据文创元素的独特性和实用性定制了一系列文创产品,并通过前沿技术手段的加持,发开了具有多样性和多元化玩法的文创产品。
此次入驻各大天文展馆和艺术展馆,正是展示了科技与文化相结合的可能性,也为未来的文化创意产业提供了新的发展方向。
这种全新的发展方向将为我们带来更加丰富、有趣的参观体验,同时也将推动科技与文化的深度融合和发展。
相关文章:

【宇宙猜想】AR文创入驻今日美术馆、北京天文馆等众多展馆,在AR互动中感受科技魅力!
近日,由「宇宙猜想」推出的AR系列文创产品先后入驻今日美术馆、北京天文馆、国家自然博物馆、上海天文馆、国家海洋馆、中华手工展馆等各大馆场并与其展开相关合作。 「宇宙猜想」致力于创造虚拟空间价值,用AR技术与文创产品碰撞出新的火花,为…...

前端面试题html
HTML DOCTYPE有什么作用? DOCTYPE是一种指示浏览器以何种HTML或XHTML规范来解析文档的声明。它能够告知浏览器网页文档使用的标记语言的类型以及版本,从而确保浏览器能够正确地展示网页内容。DOCTYPE声明通常位于HTML文档的开头,是HTML文档…...
AOSP源码下载方法,解决repo sync错误:android-13.0.0_r82
篇头 最近写文章,反复多次折腾AOSP代码,因通过网络repo sync aosp代码,能一次顺利下载的概率很低,以前就经常遇到,但从未总结,导致自己也要回头检索方法,所以觉得可以总结一下,涉及…...
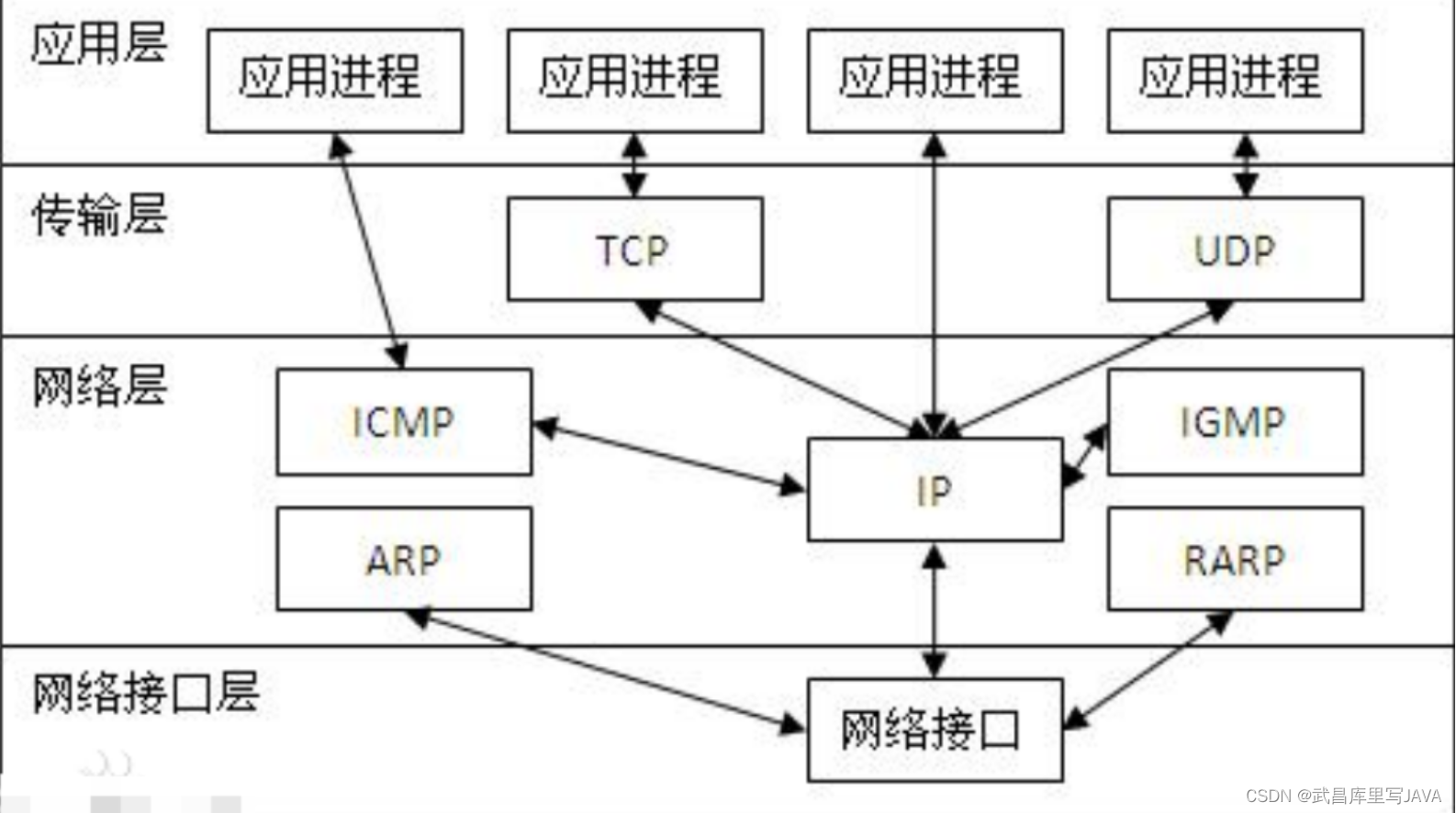
TCP:IP原理
TCP/IP 原理 TCP/IP 协议不是 TCP 和 IP 这两个协议的合称,而是指因特网整个 TCP/IP 协议族。从协议分层模型方面来讲,TCP/IP 由四个层次组成:网络接口层、网络层、传输层、应用层。 网络访问层(Network Access Layer) 网络访问层(Network …...

Java 中 Lambda 表达式的使用
目录 一、Lambda 表达式的概念 二、Lambda 表达式的语法格式 三、Lambda 表达式的案例使用 1、使用 Lambda 来实现启动线程 2、使用 Lambda 表达式实现集合的排序 3、使用 Lambda 表达式实现文件夹下的文件查找 一、Lambda 表达式的概念 Lambda 表达式是特殊的匿名内部类…...
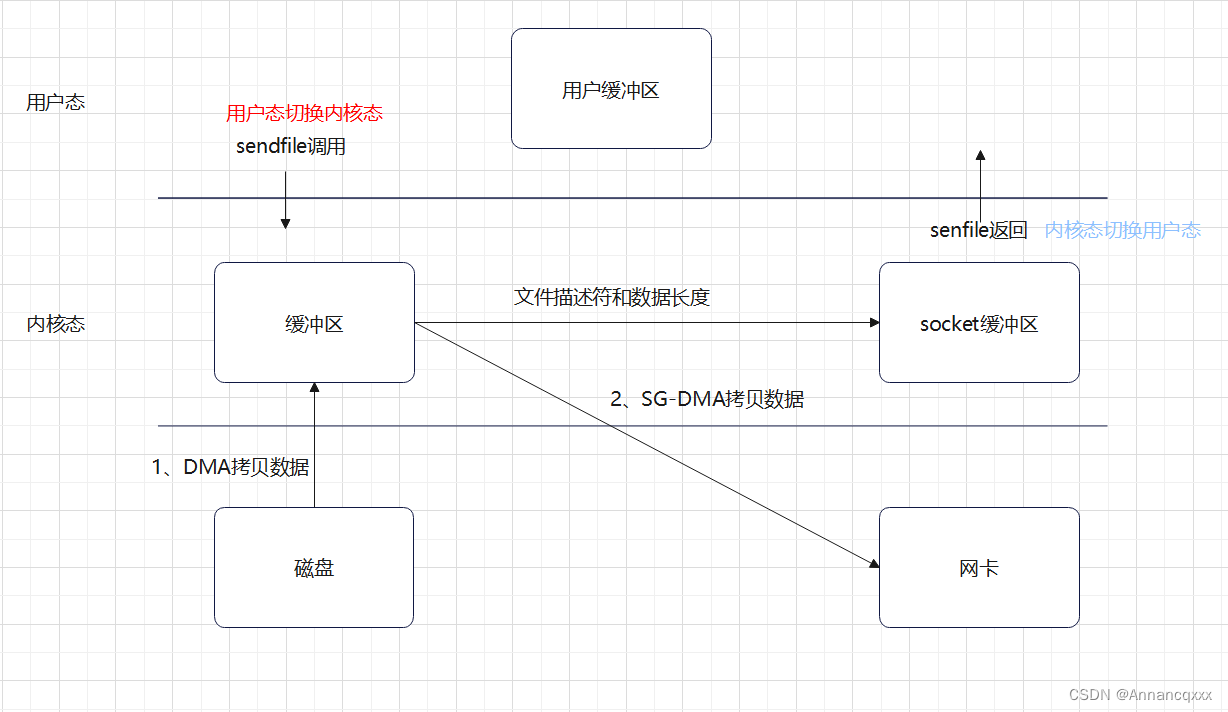
【IO】IO模型与零拷贝
前言: 正在运行的程序其实就是系统中的一个进程,操作系统会为每一个进程分配内存空间,而内存空间分为两部分,一部分是用户空间,这是用户进程访问的内存区域;另一部分是内核空间,是操作系统内核访…...

鸿蒙 - arkTs:状态管理
状态 State: 在声明式UI中,以状态驱动视图更新 状态(State):指驱动视图更新的数据(被装饰器标记的变量)视图(View):基于UI描述渲染得到的用户界面 使用示例…...
YOLOv5-Lite 树莓派4B 15帧教程
【前言】 由于v5Lite仓库遗漏了不少历史问题,最大的问题是毕业后卷起来了,找不到时间更新。 上面是这篇博客的背景,那么先说下结论,使用 v5lite-e 模型,在 树莓派4B(4G内存) 上,有三…...

2014年第三届数学建模国际赛小美赛A题吹口哨解题全过程文档及程序
2014年第三届数学建模国际赛小美赛 A题 吹口哨 原题再现: 哨子是一种小装置,当空气被迫通过开口时会发出声音。哨声的巨大而引人注目,使其对警察和体育裁判来说至关重要。当救生员、迷路的露营者或犯罪受害者使用它们时,它们可以…...
设计模式-注册模式
设计模式专栏 模式介绍模式特点应用场景注册模式和单例模式的区别代码示例Java实现注册模式Python实现注册模式 注册模式在spring中的应用 模式介绍 注册模式是一种设计模式,也称为注册树或注册器模式。这种模式将类的实例化和创建分离开来,避免在应用程…...

css 美化滚动条样式
ChatgGPT4.0国内站点: 海鲸AI-支持GPT(3.5/4.0),文件分析,AI绘图 在CSS中,你可以使用伪元素::-webkit-scrollbar以及相关的伪元素来为Webkit浏览器(如Chrome和Safari)自定义滚动条的样式。以下是一些基本的CSS规则&am…...
视频压缩不影响画质简单方法,一分钟搞定!
很多朋友在处理视频的时候都会遇到视频过大的问题,想要压缩视频的同时不影响画质,简单的方法有两种。一种是用专业的压缩软件,在压缩的时候设置一个合适的压缩比例,压缩大小的同时保持清晰度,也能提高压缩率࿰…...
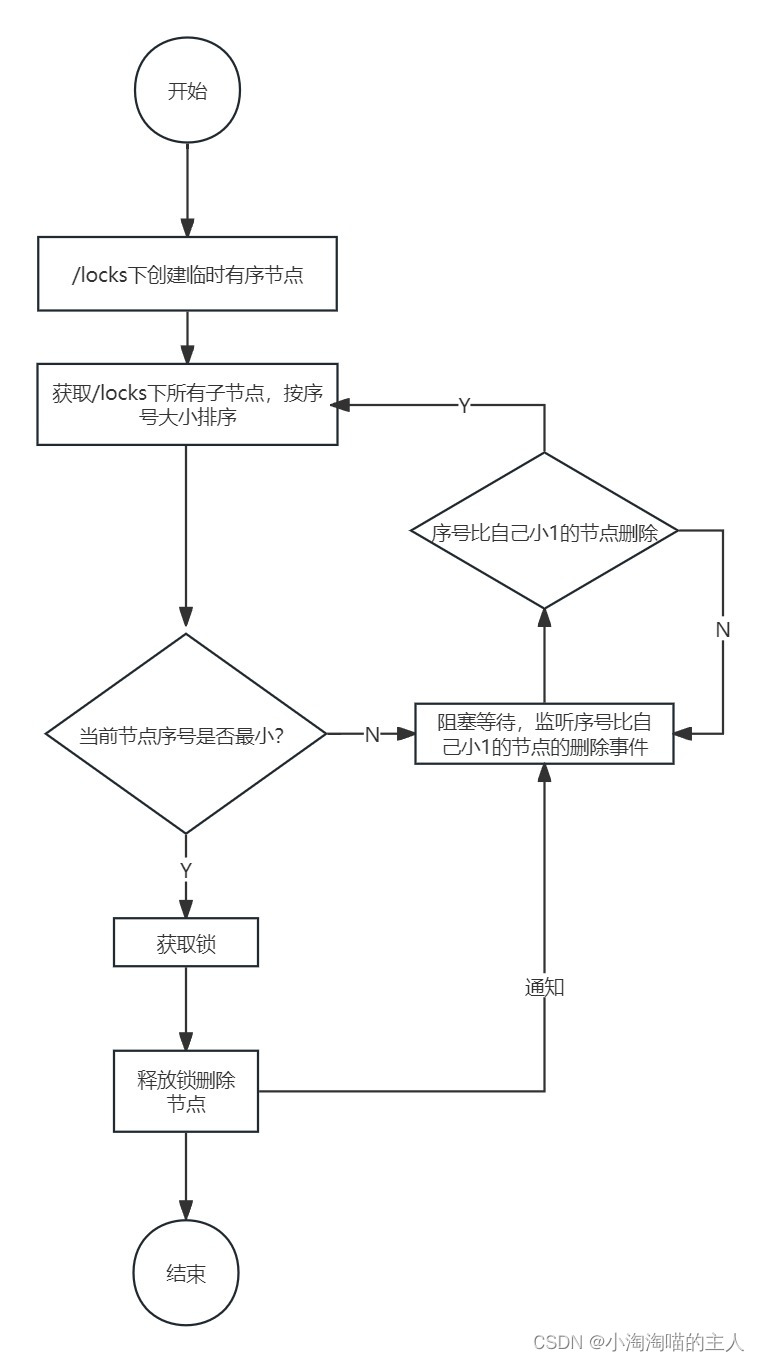
Zookeeper的使用场景
统一命名服务 利用ZooKeeper节点的树形分层结构和子节点的顺序维护能力,来为分布式系统中的资源命名。 例:分布式节点命名 分布式消息队列 1.在Zookeeper中创建一个持久节点,用作队列的根节点。队列元素的节点放在这个根节点下。 2.入队:…...

Java 面试题集锦记录
Java 面试题集锦记录 一1. SpringBoot、SpringCloud区别2. SpringCloud怎么保证服务间通信?3. Spring怎么保持高可用性、稳定性?4. 负载均衡5. [Rabbitmq](https://blog.csdn.net/qq_40985985/article/details/128013229) 怎么避免重复消费,[…...

【自然语言处理】第2部分:识别文本中的个人身份信息
自我介绍 做一个简单介绍,酒架年近48 ,有20多年IT工作经历,目前在一家500强做企业架构.因为工作需要,另外也因为兴趣涉猎比较广,为了自己学习建立了三个博客,分别是【全球IT瞭望】,【…...

C#中的.NET与.NET Framework区别
C#是一种编程语言,而.NET是一个开发平台。在.NET生态系统中,有两个相关但不同的概念:.NET和.NET Framework。 .NET Framework 发布时间: .NET Framework是最早引入的,它于2002年首次发布。它是一个用于构建Windows应…...
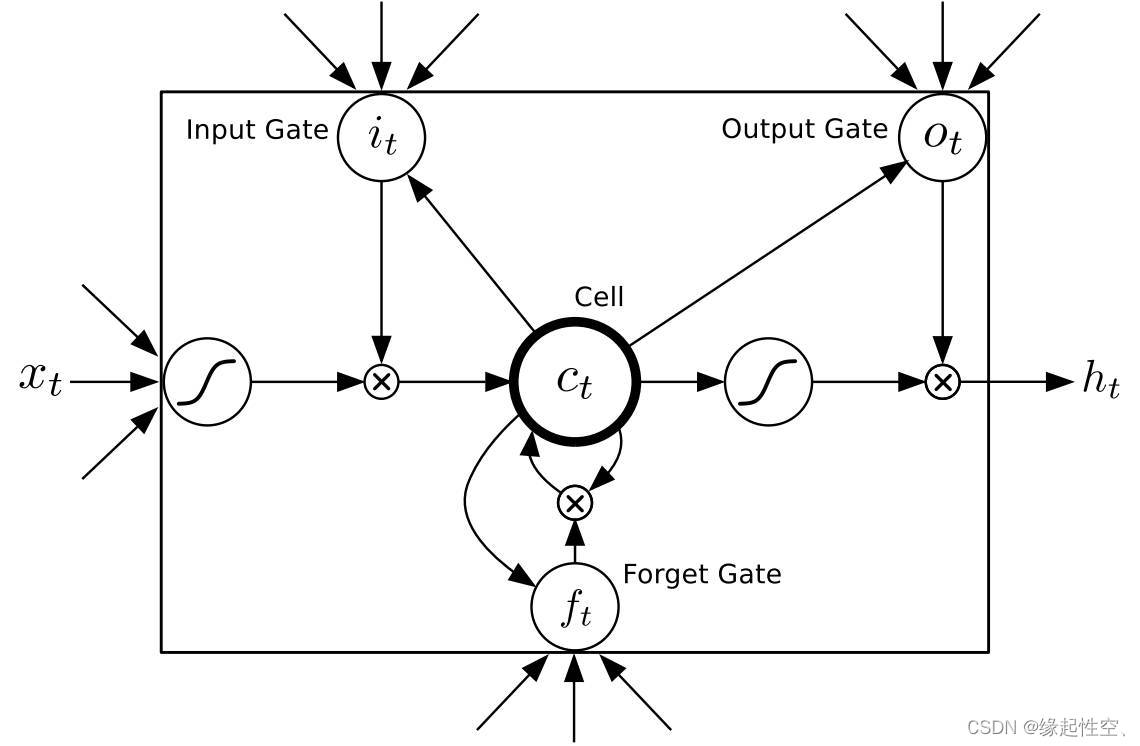
详解Keras3.0 Layer API: LSTM layer
LSTM layer 用于实现长短时记忆网络,它的主要作用是对序列数据进行建模和预测。 遗忘门(Forget Gate):根据当前输入和上一个时间步的隐藏状态,计算遗忘门的值。遗忘门的作用是控制哪些信息应该被遗忘,哪些…...
Vue和React的运行时,校验引入包的上下文差异
背景 系统使用 webpack 5 模块联邦实现微前端,有关如何实现跨应用的代码共享,可参考 如何优雅的实现跨应用的代码共享 里的第三大点。 总之,这里是其他应用使用了某个应用共享出来的reg文件,引入方式为: import REG …...

C语言中函数调用和嵌套
函数是C语言的基本组成元素 函数调用 根据函数在程序中出现的位置有下列三种函数调用方式: 将函数作为表达式调用 将函数作为表达式调用时,函数的返回值参与表达式的运算,此时要求函数必须有返回值 int retmax(100,150); 将函数作为语句…...

JVM基础篇---02
为什么需要用户自定义类加载器: 扩展类加载器的功能: Java的默认类加载器主要有三个,分别是引导类加载器、扩展类加载器和应用程序类加载器。其中,引导类加载器和扩展类加载器是由JVM实现的,用户无法修改其行为。而应用…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...

Java 与 MySQL 性能优化:MySQL 慢 SQL 诊断与分析方法详解
文章目录 一、开启慢查询日志,定位耗时SQL1.1 查看慢查询日志是否开启1.2 临时开启慢查询日志1.3 永久开启慢查询日志1.4 分析慢查询日志 二、使用EXPLAIN分析SQL执行计划2.1 EXPLAIN的基本使用2.2 EXPLAIN分析案例2.3 根据EXPLAIN结果优化SQL 三、使用SHOW PROFILE…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...
