python实现一维傅里叶变换——冈萨雷斯数字图像处理
原理
傅立叶变换,表示能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。在不同的研究领域,傅立叶变换具有多种不同的变体形式,如连续傅立叶变换和离散傅立叶变换。最初傅立叶分析是作为热过程的解析分析的工具被提出的。
定义:给定一个函数 f(t),傅立叶变换将这个函数从时域(时间域)转换到频域(频率域)上的函数 。傅立叶变换的数学表示如下:
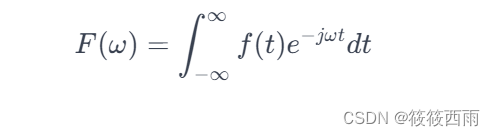
在这个表示中,F(ω) 表示频域上的复数函数,f(t) 表示时域上的函数,ω 表示频率,j 表示虚数单位。这个公式描述了将时域信号 f(t) 转换为频域信号 F(ω) 的过程。
原理:
复指数函数:傅立叶变换的核心是复指数函数ω,它表示在不同频率上的正弦和余弦振荡。傅立叶变换实际上是将信号分解为不同频率的复振幅和相位。
积分:傅立叶变换中的积分操作将时域函数给定范围内的所有时间点考虑在内,以获得频率域上的表示。这表示我们考虑了信号的所有时间信息以获取频率信息。
频谱:F(ω)表示了信号在频率ω处的振幅和相位信息。频谱显示了信号中各个频率分量的重要性。
逆变换:傅立叶变换不仅可以将信号从时域转换到频域,还可以进行逆变换,将信号从频域还原回时域,这允许我们在频域上对信号进行操作后再转换回时域。
输出如下图所示的结果:
生成包含1个、5个和10个正弦波信号的时域图和它们的FFT(傅立叶变换)的频域图,将它们放置在3x2的子图布局中。比较不同数量的正弦波信号在时域和频域上的表示。
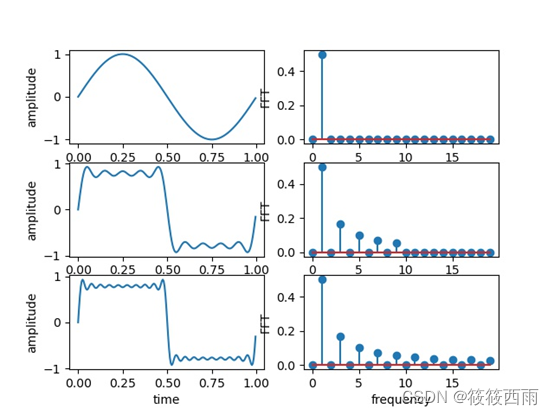
代码展示
import numpy as np
from matplotlib import pyplot as plt# 时间长度为1,采样间隔为0.005
x = np.arange(0, 1, 0.005)
# 采样点数
n = len(x)
# 由于对称性,只取单边频谱,又由于我们事先知道实验中信号的频率小于20,所以只取前20个
freq = np.arange(20)y = []
F = []
# 分别取1,5,10个正弦波叠加
for num in [1, 5, 10]:y_signal = 0for i in range(num):# 正弦波的频率为1,3,5,7...y_signal += np.sin(2*np.pi*(2*i+1)*x)/(2*i+1)y.append(y_signal)F_signal = np.fft.fft(y_signal)# 取abs是为了计算复数的幅度谱,/n是为了归一化F.append(np.abs(F_signal[range(20)])/n)_, axs = plt.subplots(3, 2)for i in range(3):axs[i, 0].plot(x, y[i])axs[i, 0].set_xlabel('time')axs[i, 0].set_ylabel('amplitude')axs[i, 1].stem(freq, F[i])axs[i, 1].set_xlabel('frequency')axs[i, 1].set_ylabel('FFT')plt.savefig('1D_FFT.jpg')
plt.show()结果展示
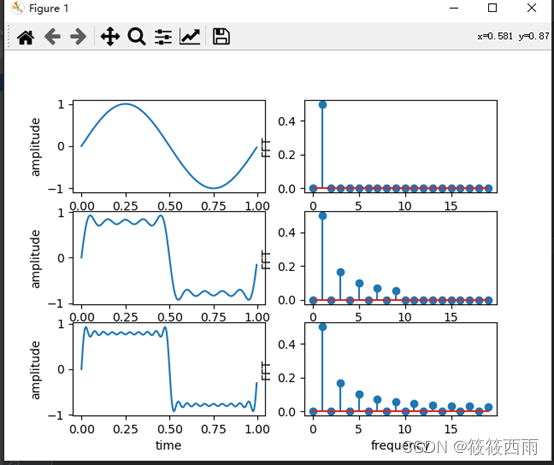
主要代码解释
创建时间向量 x:
x = np.arange(0, 1, 0.005):创建一个从0到1的时间向量 x,采样间隔为0.005秒,用于表示信号的时间范围。
获取采样点数 n:
n = len(x):计算时间向量 x 中的采样点数,以便在后续的FFT归一化中使用。
创建频率向量 freq:
freq = np.arange(20):创建一个频率向量 freq,包含从0到19的整数值,表示将计算的频率范围。
创建信号和频域数据:
使用for循环分别取1、5和10个正弦波信号,并在每个循环中生成信号,并计算其FFT。
y_signal = 0:初始化一个信号变量y_signal,用于存储叠加的正弦波信号。
在内部的for循环中,叠加不同频率的正弦波信号到y_signal。
F_signal = np.fft.fft(y_signal):计算y_signal的傅立叶变换,结果存储在F_signal中。
F.append(np.abs(F_signal[range(20)])/n):将计算的FFT结果归一化并存储在列表F中,仅保留前20个频率成分。
相关文章:

python实现一维傅里叶变换——冈萨雷斯数字图像处理
原理 傅立叶变换,表示能将满足一定条件的某个函数表示成三角函数(正弦和/或余弦函数)或者它们的积分的线性组合。在不同的研究领域,傅立叶变换具有多种不同的变体形式,如连续傅立叶变换和离散傅立叶变换。最初傅立叶分…...
表单(HTML)
<!DOCTYPE html> <html><head><meta charset"utf-8"><title>个人信息</title></head><body><h1>个人信息</h1><form><fieldset><legend>基本信息</legend><label for"…...

spripng 三级缓存,三级缓存的作用是什么? Spring 中哪些情况下,不能解决循环依赖问题有哪些
文章目录 前面有提到三级缓存,三级缓存的作用是什么?Spring 中哪些情况下,不能解决循环依赖问题: 前面有提到三级缓存,三级缓存的作用是什么? 上一篇:https://blog.csdn.net/weixin_44797327/a…...

elasticsearch系列六:索引重建
概述 我们再起初创建索引的时候由于数据量、业务增长量都并不大,常常不需要搞那么多分片或者说某些字段的类型随着业务的变化,已经不太满足未来需求了,再或者由于集群上面索引分布不均匀导致节点直接容量差异较大等等这些情况,此时…...
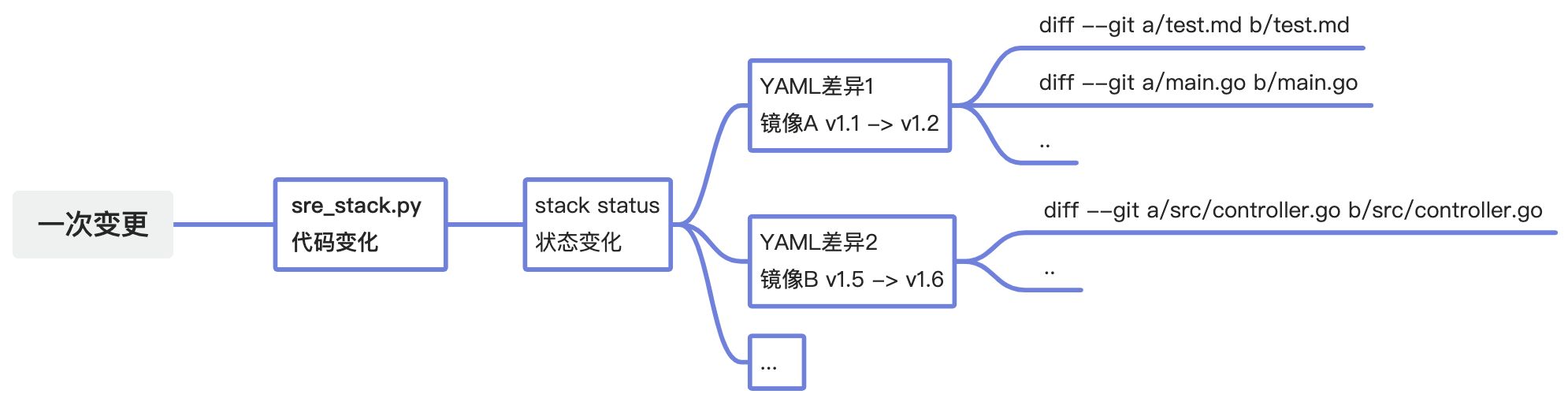
GitOps实践指南:GitOps能为我们带来什么?
Git,作为开发过程中的核心工具,提供了强大的版本控制功能。即便在写代码的时候稍微手抖一下,我们也能通过 Git 的差异对比(diff)轻松追踪到庞大工程中的问题,确保代码的准确与可靠。这种无与伦比的自省能力…...
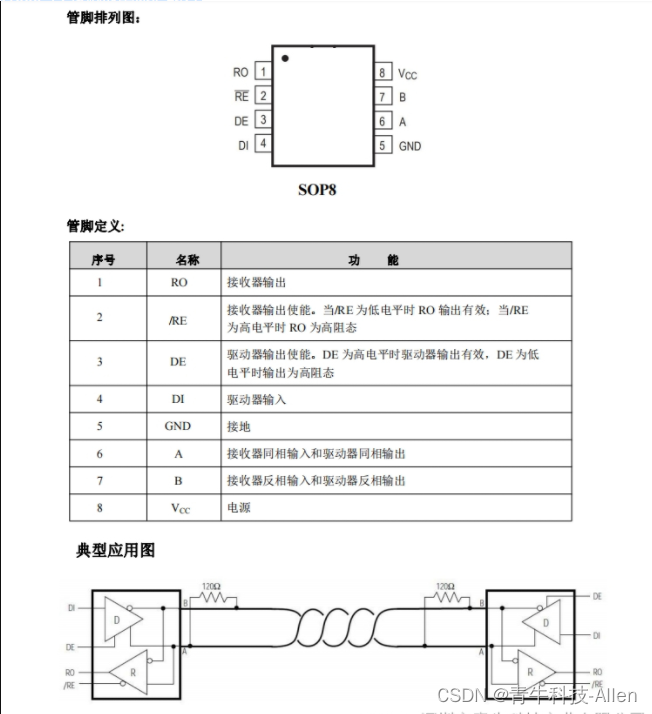
D3485国产芯片+5V工作电压, 内置失效保护电路采用SOP8封装
D3485是一款5V供电、半双工的RS-485收发器,芯片内部包含一路驱动器和路接收器。D3485使用限摆率驱动器,能显著减小EMI和由于不恰当的终端匹配电缆所引起的反射,并实现高达10Mbps的无差错数据传输。D3485内置失效保护电路,保证接收…...

devops使用
官方文档 使用 Git 进行代码 - Azure DevOps | Microsoft Learn...

AI训练师常用的ChatGPT通用提示词模板
AI模型选择:如何选择合适的AI模型? 数据集准备:如何准备用于训练的数据集? 数据预处理:如何对待训练数据进行预处理? 特征工程:如何进行特征选择和特征工程? 超参数调整…...
)
Java加密算法工具类(AES、DES、MD5、RSA)
整理了有关加密算法工具类,结合了几个博客以及自己改良后可直接使用,主要介绍以下四种加密方式:AES、DES、MD5、RSA,详细介绍都在注释里面有讲。 一、AES import com.alibaba.fastjson.JSONObject; import java.nio.charset.Sta…...

探索Go语言的魅力:一门简洁高效的编程语言
介绍Go语言: Go,也被称为Golang,是由Google开发的一门开源编程语言。它结合了现代编程语言的优点,拥有高效的并发支持和简洁的语法,使其成为构建可伸缩、高性能应用的理想选择。 Go语言的特性: 并发编程…...

【用unity实现100个游戏之19】制作一个3D传送门游戏,实现类似鬼打墙,迷宫,镜子,任意门效果
最终效果 文章目录 最终效果素材第一人称人物移动开门效果显示原理渲染相机跟着我们视角移动门的摄像机跟着我们旋转近裁剪面设置传送配置代码实现传送效果结束完结素材 https://assetstore.unity.com/packages/3d/props/interior/door-free-pack-aferar-148411...
框架基于restAPI协议规范的知识点总结)
DRF(Django Rest Framework)框架基于restAPI协议规范的知识点总结
Django Rest Framework学习 一、初识DRF组件 1.1 FBV和CBV FBV:function based view from django.shortcuts import render, HttpResponse # 这种是基于FBV模式 函数模式实现Views函数 def login(request):if request.method GET:return HttpResponse("Get…...
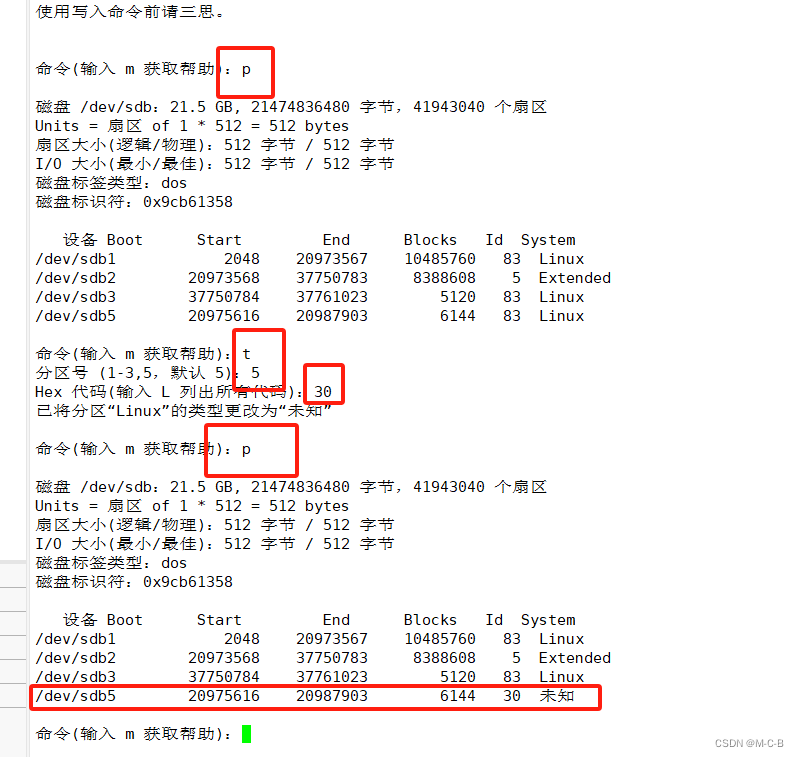
Linux磁盘与文件系统管理
目录 在linux系统中使用硬盘 磁盘的数据结构 磁盘接口类型 字母含义 MBR磁盘分区 分区类型 分区的缺点 文件系统的 文件系统有什么作用 文件系统的修复 检测并确认新磁盘 参看磁盘信息 查看磁盘信息 添加磁盘 查看添加磁盘情况:sda系统磁盘ÿ…...

数字魔法AI绘画的艺术奇迹-用Stable Diffusion挑战无限可能【文末送书-12】
文章目录 前言一. 技术原理1.1 发展历程 二.对艺术领域的影响三. 挑战与机遇四.AI魔法绘画:用Stable Diffusion挑战无限可能【文末送书-12】4.1 粉丝福利:文末推荐与福利免费包邮送书! 前言 随着人工智能技术的迅猛发展,AI在各个…...
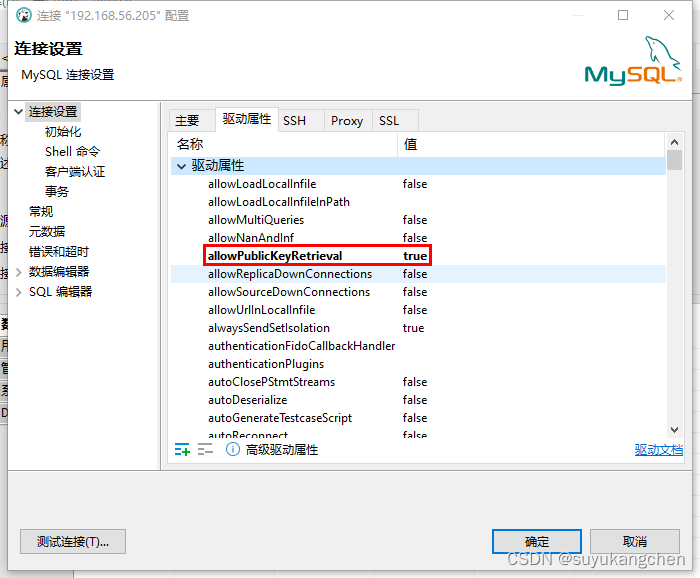
【docker实战】02 用docker安装mysql
本示例采用bitnami的镜像进行安装MySQL 一、镜像搜索 先搜索一下mysql有哪些镜像 [rootlocalhost ~]# docker search mysql NAME DESCRIPTION STARS OFFICIAL AUTOMATED mysql …...

循环渲染ForEach
目录 1、接口说明 2、键值生成规则 3、组件创建规则 3.1、首次渲染 3.2、非首次渲染 4、使用场景 4.1、数据源不变 4.2、数据源组项发生变化 4.3、数据源数组项子属性变化 5、反例 5.1、渲染结果非预期 5.2、渲染性能降低 Android开发中我们有ListView组件、GridVi…...

纷享销客华为云:如何让企业多一个选择?
纷享销客携手华为云推出多项联合解决方案,为企业的数字化提供了一个新选择。12月12日,纷享销客&华为云联合解决方案发布会在北京举办。本次发布会以“「CRM云」让企业多一个选择”为主题,来自行业头部企业的CEO、CIO、业务负责人等&#…...

前端实现断点续传文件
公司要求实现的功能,大概思路是将上传的文件通过jsZip压缩后,进行切片,留一下总切片,当前片,并把这些数据给后端,至于前端的校验,是由Md5完成的,验证文件唯一性,这样下次…...
算法篇)
复试 || 就业day01(2023.12.27)算法篇
文章目录 前言两数之和存在重复元素 II好数对的数目总持续时间可被 60 整除的歌曲 前言 💫你好,我是辰chen,本文旨在准备考研复试或就业 💫文章题目大多来自于 leetcode,当然也可能来自洛谷或其他刷题平台 Ὂ…...
JavaWeb——JQuery
文章目录 JQuery 是什么?jQuery 的原理示意图JQuery 基本开发步骤jQuery 对象和 DOM 对象将dom对象转为JQuery对象jQuery 对象转成 DOM 对象jQuery 选择器基本选择器基础过滤选择器JQuery 是什么? 基本介绍 jQuery 是一个快速的,简洁的 javaScript 库,使用户能更方便地处理…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...
