八种常见顺序存储的算法
目录
1、线性枚举
1)问题描述
2)动图演示
3)示例说明
4)算法描述
5)源码详解
2、前缀和差分
1)问题描述
2)动图演示
3)样例分析
4)算法描述
5)源码详解
3、双指针
1)问题描述
2)动图演示
3)样例说明
4)算法描述
5)源码详解
4、二分枚举
1)问题描述编辑
2)动图演示
3)样例说明
4)算法描述
5)源码详解
5、三分枚举
6、插入排序
1)问题描述
2)动图演示
3)样例说明
4)算法描述
5)源码详解
7、选择排序
1)问题描述
2)动图演示
3)样例说明
4)算法描述
5)源码详解
8、冒泡排序
1)问题描述
2)动图演示
3)样例说明
4)算法描述
5)源码详解
1、线性枚举
1)问题描述

2)动图演示

3)示例说明
蓝色的数据代表的是数组数据,红色的数据代表当前枚举到的数据,这样就可以遍历所有的数据进行逻辑处理了。
4)算法描述
遍历数组,进行条件判断,条件满足则执行逻辑。这里的条件就是 枚举到的数 是否小于 当前最小值,执行逻辑为 将 当前枚举到的数 赋值给 当前最小值;
5)源码详解
int findMin(int* nums, int numsSize){int i, min = 100000;for(i = 0; i < numsSize; ++i) { // (1)if(nums[i] < min) { // (2)min = nums[i];}}return min; // (3)
}- (1) 遍历数组中所有的数;
- (2) 如果 当前枚举到的数 比记录的变量
min小,则将它赋值给min;否则,不做任何处理; - (3) 最后,
min中存储的就是整个数组的最小值。
2、前缀和差分
1)问题描述

2)动图演示
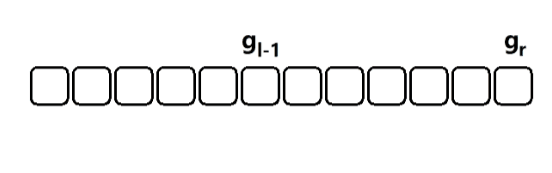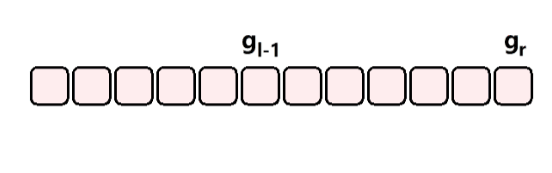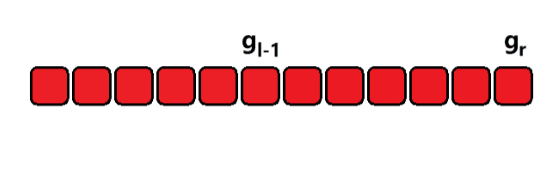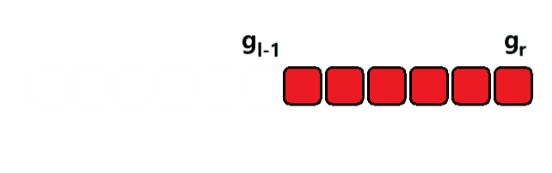
3)样例分析
如上图所示,只需要记录一个前缀和,然后就可以通过一次减法将区间的值计算出来。时间复杂度 O(1)。这种就是差分的思想。
原理:
sum[r] = a[1] + a[2] + a[3] + a[l-1] + a[l] + a[l + 1] ...... a[r];
sum[l - 1] = a[1] + a[2] + a[3] + a[l - 1];
sum[r] - sum[l - 1] = a[l] + a[l + 1] + ......+ a[r];
4)算法描述
第一个枚举,利用一个数组sum,存储前 i 个元素的和。
第二个枚举,读入 m 组数据 l,r,对每组数据,通过 O(1) 获取答案,即sum[r] - sum[l - 1]。
5)源码详解
int sum[maxn];
int* prefixSum(int* nums, int numsSize, int m, int *l, int *r){int i;int *ret;for(i = 0; i < numsSize; ++i) {sum[i] = nums[i];if(i) sum[i] += sum[i-1]; // (1) }ret = (int *) malloc( m * sizeof(int) ); // (2) for(i = 0; i < m; ++i) {int leftsum = l[i] == 0 ? 0 : sum[l[i]-1]; // (3) int rightsum = sum[r[i]];ret[i] = rightsum - leftsum; // (4) }return ret;
}- (1) 计算前缀和;
- (2) 需要返回的数组;
- (3) 这里是为了防止数组下标越界;
- (4) 核心 O(1) 的差分计算;
3、双指针
1)问题描述

2)动图演示

3)样例说明
维护两个指针 i 和 j,区间 [i,j] 内的子串,应该时刻保持其中所有字符不重复,一旦发现重复字符,就需要自增 i(即执行 i = i + 1);否则,执行 j = j + 1,直到 j 不能再增加为止。
过程中,记录合法情况下 j − i + 1 的最大值。
4)算法描述
如上文所述,这种利用问题特性,通过两个指针,不断调整区间,从而求出问题最优解的算法就叫 “尺取法”,由于利用的是两个指针,所以又叫 “双指针” 算法。
这里 “尺” 的含义,主要还是因为这类问题,最终要求解的都是连续的序列(子串),就好比一把尺子一样,故而得名。
算法描述如下:
1)初始化 i = 0, j = i − 1,代表一开始 “尺子” 的长度为 0;
2)增加 “尺子” 的长度,即 j = j + 1;
3)判断当前这把 “尺子” [i,j] 是否满足题目给出的条件:
3.a)如果不满足,则减小 “尺子” 长度,即 i = i + 1,回到 3);
3.b)如果满足,记录最优解,回到 2);
- 上面这段文字描述的比较官方,其实这个算法的核心,只有一句话:
满足条件时,j++;不满足条件时,i++;
- 如图所示,当区间 [i,j] 满足条件时,用蓝色表示,此时 j 自增;反之闪红,此时 i 自增。

5)源码详解
int getmaxlen(int n, char *str, int& l, int& r) {int ans = 0, i = 0, j = -1, len; // 1)memset(h, 0, sizeof(h)); // 2)while (j++ < n - 1) { // 3)++h[ str[j] ]; // 4)while (h[ str[j] ] > 1) { // 5)--h[ str[i] ];++i;}len = j - i + 1; if(len > ans) // 6)ans = len, l = i, r = j;}return ans;
}- 1)初始化
i = 0, j = -1,代表 s[i:j] 为一个空串,从空串开始枚举; - 2)需要维护一个哈希表,哈希表记录的是当前枚举的区间 s[i:j] 中每个字符的个数;
- 3)只推进子串的右端点;
- 4)在哈希表中记录字符的个数;
- 5)当
h[ str[j] ] > 1满足时,代表出现了重复字符str[j],这时候左端点 i 推进,直到没有重复字符为止; - 6)记录当前最优解的长度
j - i + 1,更新; - 这个算法执行完毕,我们就可以得到最长不重复子串的长度为 ans,并且 i 和 j 这两个指针分别只自增 n 次,两者自增相互独立,是一个相加而非相乘的关系,所以这个算法的时间复杂度为 O(n) 。
4、二分枚举
1)问题描述
2)动图演示

3)样例说明
需要找值为 5 的这个元素。
黄色箭头代表都是左区间端点 l,红色箭头代表右区间端点 r。蓝色的数据为数组数据,绿色的数字代表的是数组下标,初始化 l = 0,r = 7,由于数组有序,则可以直接折半,令 mid =(l+r)/2=3,则 55 一定落入区间 [0,3],这时候令 r = 3,继续执行,直到 l > r 结束迭代。
最后,当 mid = 2 时,找到数据 5。
4)算法描述
a)令初始情况下,数组下标从 0 开始,且数组长度为 n,则定义一个区间,它的左端点是 l = 0,右端点是 r = n−1;
b)生成一个区间中点 mid = (l+r)/2,并且判断 mid 对应的数组元素和给定的目标值的大小关系,主要有三种:
b.1)目标值 等于 数组元素,直接返回 mid;
b.2)目标值 大于 数组元素,则代表目标值应该出现在区间 [mid+1,r],迭代左区间端点:l=mid+1;
b.3)目标值 小于 数组元素,则代表目标值应该出现在区间 [l,mid−1],迭代右区间端点:r=mid−1;
c)如果这时候 l>r,则说明没有找到目标值,返回 −1;否则,回到 b)继续迭代。
5)源码详解
int search(int *nums, int numsSize, int target) {int l = 0, r = numsSize - 1; // (1)while(l <= r) { // (2)int mid = (l + r) >> 1; // (3)if(nums[mid] == target) { return mid; // (4)}else if(target > nums[mid]) {l = mid + 1; // (5)}else if(target < nums[mid]) {r = mid - 1; // (6)}}return -1; // (7)
}- (1) 初始化区间左右端点;
- (2) 一直迭代左右区间的端点,直到 左端点 大于 右端点 结束;
- (3)
>> 1等价于除 2,也就是这里mid代表的是l和r的中点; - (4)
nums[mid] == target表示正好找到了这个数,则直接返回下标mid; - (5)
target > nums[mid]表示target这个数在区间 [���+1,�][mid+1,r] 中,所以才有左区间赋值如下:l = mid + 1; - (6)
target < nums[mid]表示target这个数在区间 [�,���−1][l,mid−1] 中,所以才有右区间赋值如下:r = mid - 1; - (7) 这一步呼应了 (2),表示这不到给定的数,直接返回
-1;
5、三分枚举
三分枚举 类似 二分枚举 的思想,也是将区间一下子砍掉一块基本完全不可能的块,从而减小算法的时间复杂度。只不过 二分枚举 解决的是 单调性 问题。而 三分枚举 解决的是 极值问题。
6、插入排序
1)问题描述
给定一个 n 个元素的数组,数组下标从 0 开始,采用「 插入排序 」将数组按照 「升序」排列。
2)动图演示

3)样例说明
| 图示 | 含义 |
|---|---|
| 蓝色柱形 | 代表尚未排好序的数 |
| 绿色柱形 | 代表正在执行 比较 和 移动 的数 |
| 橙色柱形 | 代表已经排好序的数 |
| 红色柱形 | 代表待执行插入的数 |
我们看到,首先需要将 「第二个元素」 和 「第一个元素」 进行 「比较」,如果 前者 小于等于 后者,则将 后者 进行向后 「移动」,前者 则执行插入;
然后,进行第二轮「比较」,即 「第三个元素」 和 「第二个元素」、「第一个元素」 进行 「比较」, 直到 「前三个元素」 保持有序 。
最后,经过一定轮次的「比较」 和 「移动」之后,一定可以保证所有元素都是 「升序」 排列的。
4)算法描述
整个算法的执行过程分以下几步:
1) 循环迭代变量 i=1→n−1;
2) 每次迭代,令 x=a[i],j=i−1,循环执行比较 x 和 a[j],如果产生 x≤a[j] 则执 行 a[j+1]=a[j]。然后执行j=j+1,继续执行 2);否则,跳出循环,回到 1)。
5)源码详解
#include <stdio.h>int a[1010];void Input(int n, int *a) {for(int i = 0; i < n; ++i) {scanf("%d", &a[i]);}
}void Output(int n, int *a) {for(int i = 0; i < n; ++i) {if(i)printf(" ");printf("%d", a[i]);}puts("");
}void InsertSort(int n, int *a) { // (1)int i, j; for(i = 1; i < n; ++i) {int x = a[i]; // (2)for(j = i-1; j >= 0; --j) { // (3)if(x <= a[j]) { // (4)a[j+1] = a[j]; // (5)}elsebreak; // (6)}a[j+1] = x; // (7)}
} int main() {int n;while(scanf("%d", &n) != EOF) {Input(n, a);InsertSort(n, a);Output(n, a);}return 0;
} - (1)
void InsertSort(int n, int *a)为 插入排序 的实现,代表对a[]数组进行升序排序。 - (2) 此时
a[i]前面的i-1个数都认为是排好序的,令x = a[i]; - (3) 逆序的枚举所有的已经排好序的数;
- (4) 如果枚举到的数
a[j]比需要插入的数x大,则当前数往后挪一个位置; - (5) 执行挪位置的 �(1)O(1) 操作;
- (6) 否则,跳出循环;
- (7) 将
x插入到合适位置;
7、选择排序
1)问题描述
给定一个 �n 个元素的数组,数组下标从 00 开始,采用「 选择排序 」将数组按照 「升序」排列。
2)动图演示

3)样例说明
| 图示 | 含义 |
|---|---|
| 蓝色柱形 | 代表尚未排好序的数 |
| 绿色柱形 | 代表正在执行 比较 的数 |
| 橙色柱形 | 代表已经排好序的数 |
| 红色柱形 | 有两种:1、记录最小元素 2、执行交换的元素 |
我们发现,首先从 「第一个元素」 到 「最后一个元素」 中选择出一个 「最小的元素」,和 「第一个元素」 进行 「交换」;
然后,从 「第二个元素」 到 「最后一个元素」 中选择出一个 「最小的元素」,和 「第二个元素」 进行 「交换」。
最后,一定可以保证所有元素都是 「升序」 排列的。
4)算法描述
整个算法的执行过程分以下几步:
1) 循环迭代变量 i=0→n−1;
2) 每次迭代,令 min=i,j=i+1;
3) 循环执行比较 a[j] 和 a[min],如果产生 a[j]<a[min] 则执行 min=j。执行 j=j+1,继续执行这一步,直到 j==n;
4) 交换 a[i] 和 a[min],回到 1)。
5)源码详解
#include <stdio.h>int a[1010];void Input(int n, int *a) {for(int i = 0; i < n; ++i) {scanf("%d", &a[i]);}
}void Output(int n, int *a) {for(int i = 0; i < n; ++i) {if(i)printf(" ");printf("%d", a[i]);}puts("");
}void Swap(int *a, int *b) {int tmp = *a;*a = *b;*b = tmp;
}void SelectionSort(int n, int *a) { // (1)int i, j;for(i = 0; i < n - 1; ++i) { // (2)int min = i; // (3)for(j = i+1; j < n; ++j) { // (4)if(a[j] < a[min]) {min = j; // (5)}}Swap(&a[i], &a[min]); // (6) }
}int main() {int n;while(scanf("%d", &n) != EOF) {Input(n, a);SelectionSort(n, a);Output(n, a);}return 0;
} - (1)
void SelectionSort(int n, int *a)为选择排序的实现,代表对a[]数组进行升序排序。 - (2) 从首元素个元素开始进行 n−1 次跌迭代。
- (3) 首先,记录
min代表当前第 i 轮迭代的最小元素的下标为 i。 - (4) 然后,迭代枚举第 i+1 个元素到 最后的元素。
- (5) 选择一个最小的元素,并且存储下标到
min中。 - (6) 将 第 i 个元素 和 最小的元素 进行交换。
8、冒泡排序
1)问题描述
给定一个 n 个元素的数组,数组下标从 0 开始,采用「 冒泡排序 」将数组按照 「升序」排列。
2)动图演示

3)样例说明
| 图示 | 含义 |
|---|---|
| 蓝色柱形 | 代表尚未排好序的数 |
| 绿色柱形 | 代表正在执行比较的两个数 |
| 黄色柱形 | 代表已经排好序的数 |
我们看到,首先需要将 「第一个元素」 和 「第二个元素」 进行 「比较」,如果 前者 大于 后者,则进行 「交换」,然后再比较 「第二个元素」 和 「第三个元素」 ,以此类推,直到 「最大的那个元素」 被移动到 「最后的位置」 。
然后,进行第二轮「比较」,直到 「次大的那个元素」 被移动到 「倒数第二的位置」 。
最后,经过一定轮次的「比较」 和 「交换」之后,一定可以保证所有元素都是 「升序」 排列的。
4)算法描述
整个算法的执行过程分以下几步:
1) 循环迭代变量 i=0→n−1;
2) 每次迭代,令 j=i,循环执行比较 a[j] 和 a[j+1],如果产生 a[j]>a[j+1] 则交换两者的值。然后执行 j=j+1,这时候对 j 进行判断,如果 j≥n−1,则回到 1),否则继续执行 2)。
5)源码详解
#include <stdio.h>int a[1010];void Input(int n, int *a) {for(int i = 0; i < n; ++i) {scanf("%d", &a[i]);}
}void Output(int n, int *a) {for(int i = 0; i < n; ++i) {if(i)printf(" ");printf("%d", a[i]);}puts("");
}void Swap(int *a, int *b) {int tmp = *a;*a = *b;*b = tmp;
}void BubbleSort(int n, int *a) { // (1)bool swapped;int last = n;do {swapped = false; // (2)for(int i = 0; i < last - 1; ++i) { // (3)if(a[i] > a[i+1]) { // (4)Swap(&a[i], &a[i+1]); // (5)swapped = true; // (6)}}--last;}while (swapped);
} int main() {int n;while(scanf("%d", &n) != EOF) {Input(n, a);BubbleSort(n, a);Output(n, a);}return 0;
} - (1)
void BubbleSort(int n, int *a)为冒泡排序的实现,代表对a[]数组进行升序排序。 - (2)
swapped标记本轮迭代下来,是否有元素产生了交换。 - (3) 每次冒泡的结果,会执行
last的自减,所以待排序的元素会越来越少。 - (4) 如果发现两个相邻元素产生逆序,则将它们进行交换。保证右边的元素一定不比左边的小。
- (5)
swap实现了元素的交换,这里需要用&转换成地址作为传参。 - (6) 标记更新。一旦标记更新,则代表进行了交换,所以下次迭代必须继续。
相关文章:

八种常见顺序存储的算法
目录 1、线性枚举 1)问题描述 2)动图演示 3)示例说明 4)算法描述 5)源码详解 2、前缀和差分 1)问题描述 2)动图演示 3)样例分析 4)算法描述 5)源码…...

Leetcod面试经典150题刷题记录 —— 栈篇
Leetcod面试经典150题刷题记录 —— 栈篇 1. 有效的括号2. 简化路径3. 最小栈4. 逆波兰表达式求值5. 基本计算器 1. 有效的括号 题目链接:有效的括号 - leetcode 题目描述: 给定一个只包括 ( ,),{,},[&…...

【Qt-QThread-QQueue】
Qt编程指南 ■ QThread■ 示例■ QQueue■■■ QThread ■ 示例 #include <QThread> class myThread : public QThread {Q_OBJECT signals...
电子握力器改造
toy_hand_game 介绍 消耗体力玩具,使用握力器(Grip Strengthener)控制舵机旋转。 开始设想是控制丝杆电机滑动,两套设备就可以控制两个丝杆电机进行“模拟拔河”,后续发现硬件设计错误,ULN2003不能控制两相四线电机,…...

3D展2D数学原理
今年早些时候,我为 MAKE 杂志写了一篇教程,介绍如何制作视频游戏角色的毛绒动物。 该技术采用给定的角色 3D 模型及其纹理,并以编程方式生成缝纫图案。 虽然我已经编写了一般摘要并将源代码上传到 GitHub,但我在这里编写了对使这一…...
MacOS+Homebrew+iTerm2+oh my zsh+powerlevel10k美化教程
MacOS终端 你是否已厌倦了MacOS终端的大黑屏? 你是否对这种美观的终端抱有兴趣? 那么,接下来我将会教你用最简单的方式来搭建一套自己的终端。 Homebrew的安装 官网地址:Homebrew — The Missing Package Manager for macOS (o…...
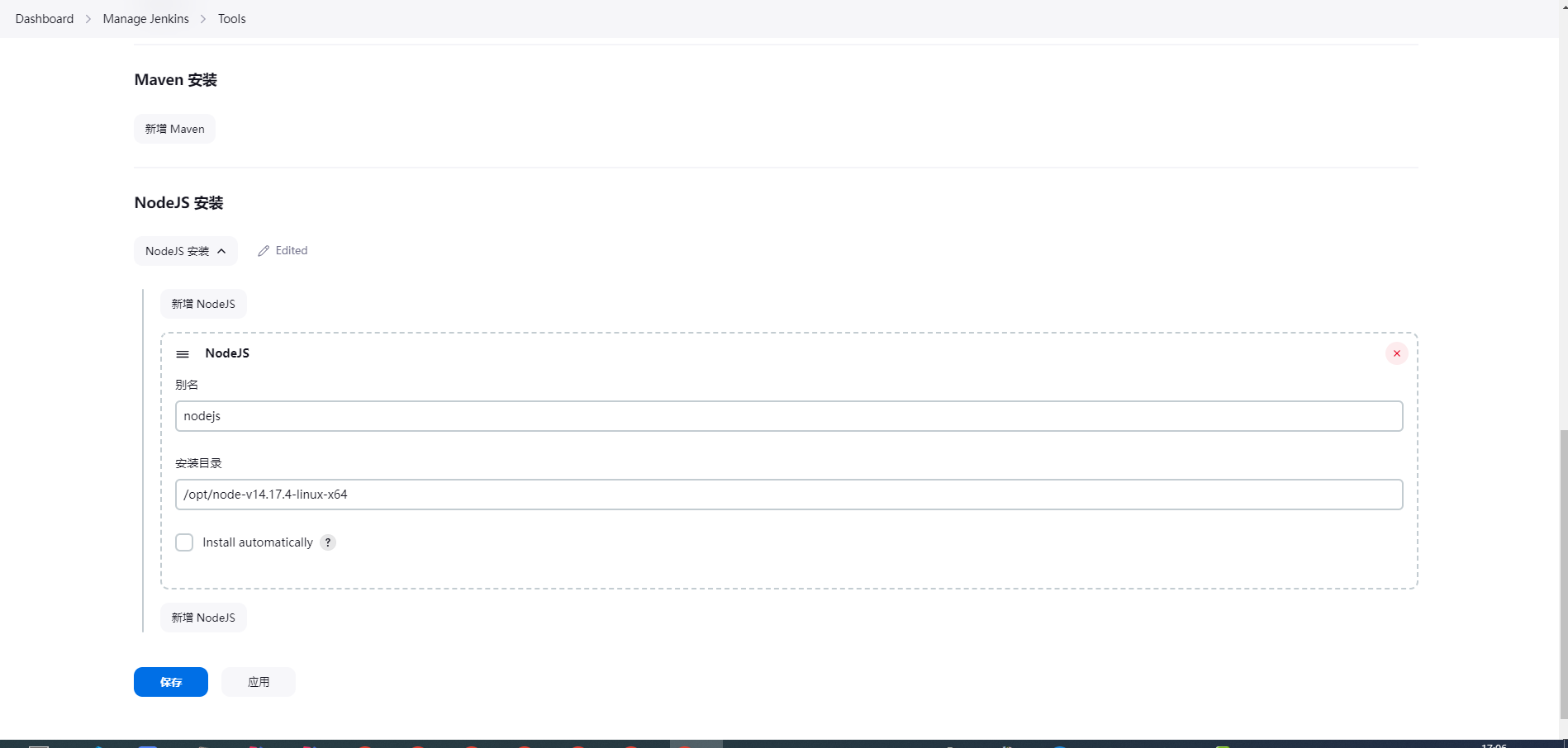
jenkins解决工具找不到的问题
--------------------------插件选择版本最好能跟服务器对上...

Android : 画布的使用 简单应用
示例图: MyView.java: package com.example.demo;import android.content.Context; import android.graphics.BitmapFactory; import android.graphics.Canvas; import android.graphics.Color; import android.graphics.Paint; import android.view.Vi…...

紫光展锐5G扬帆出海 | 东南亚成为5G新热土
东南亚是一块充满活力和潜力的市场,这里人口基数大、年轻消费群体占比高,电子市场在过去几年显著增长。 增速“狂飙”的东南亚手游 近年来,东南亚手游下载量逐年增长,2023 年第一季度下载量突破 21 亿次,贡献了全球近…...
STM32 学习(一)新建工程
本课程使用的stm32型号 引脚定义,有FT能接5v,没有FT能接3.3v 启动配置 第二种启动模式中,系统存储器中存放了一部分Bootloader程序,该程序可以接收串口的数据,然后刷新到主闪存中,这样就可以使用串口下载程…...

ROBOGUIDE教程:FANUC机器人固定点焊焊接虚拟仿真
目录 概述 机器人系统创建 焊接工件模型创建 机器人抓手工具添加与工件安装 工作台添加与工件安装 固定点焊焊枪支架模型创建与组装 固定点焊焊枪添加与配置 机器人远程TCP标定(核心内容) 远程TCP手动测试 远程TCP指令介绍 机器人仿真程序编写 机器人示教编程 机…...
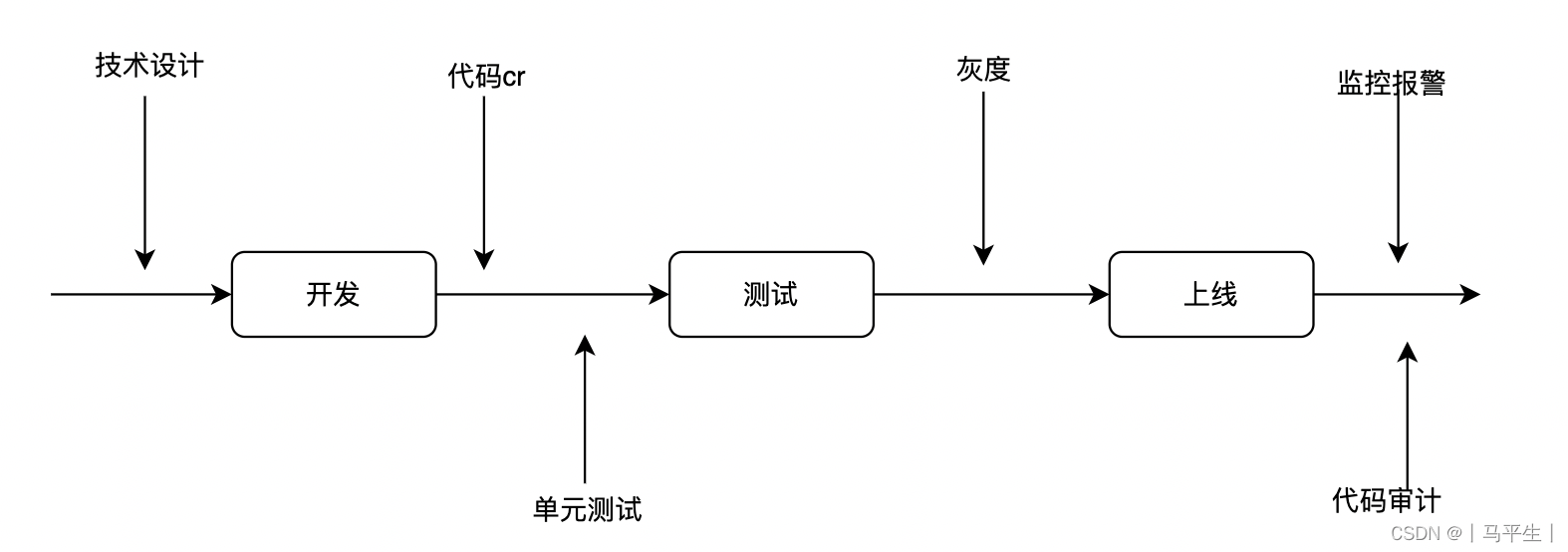
代码审计必要性探讨
1、背景 为了保证代码的质量,需要一系列的流程来进行保证: 今天要探讨的是代码审计的必要性。 2、代码审计 代码审计的做法多种多样,我理解必须解决以下问题 ,才可能有效: 核心:审计的本质是对比&#…...

SpringBoot-Shiro
Apache Shiro:https://shiro.apache.org/ 依赖 <dependency><groupId>org.apache.shiro</groupId><artifactId>shiro-spring</artifactId><version>1.4.1</version> </dependency>ShiroConfig.java Configuratio…...
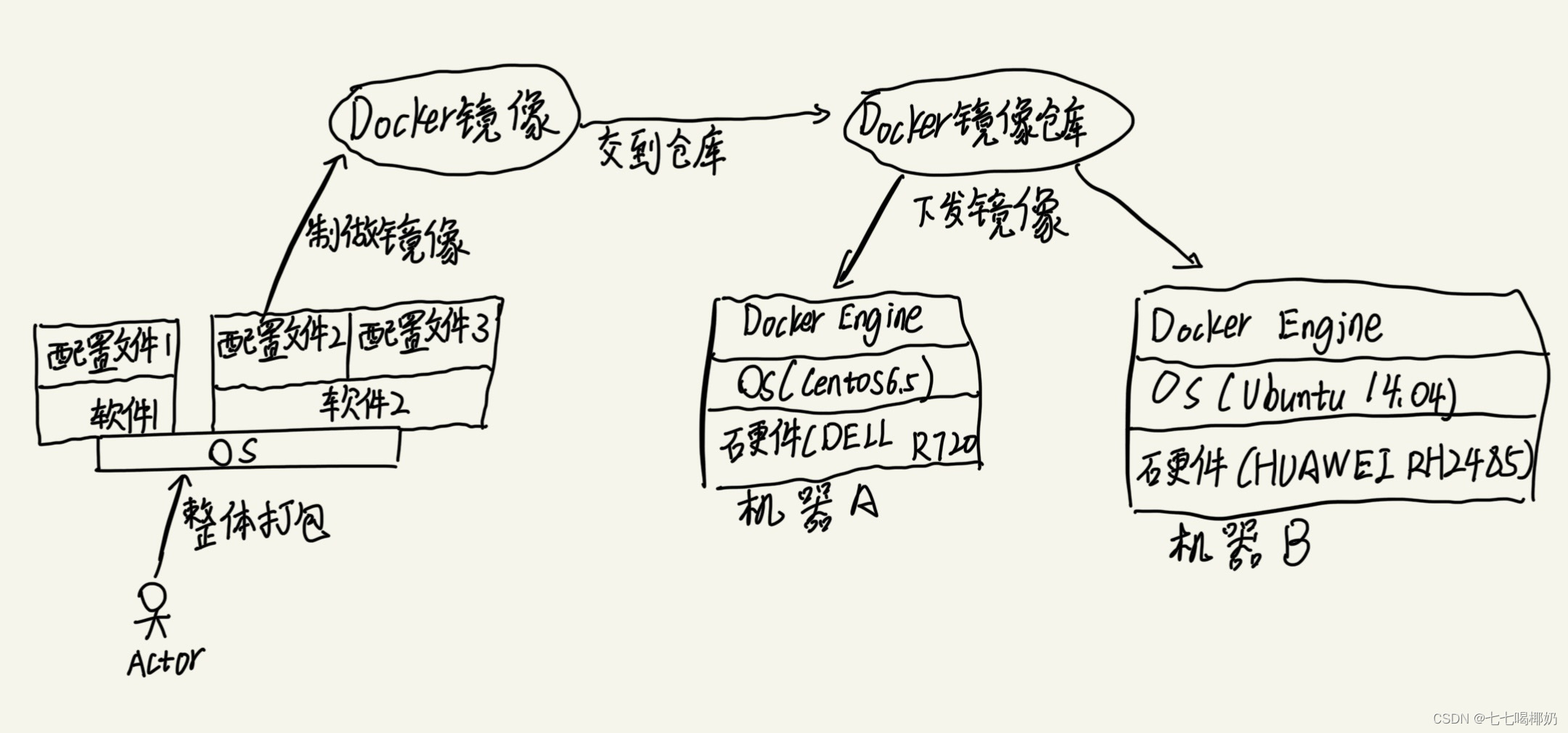
认识Docker
大家好,这里是七七,今天起开起我们的Docker技术篇,本文是介绍Docker的,不介绍如何使用和安装Docker,只是单纯的介绍Docker。 目录 一、历史 二、Docker究竟是什么 三、Docker的结构与特性 1、Docker仓库 2、Dock…...
uniapp的分包使用记录
UniApp的分包是一种将应用代码划分为多个包的技术。分包的核心思想是将不同部分的代码划分为不同的包,按需加载,从而提高应用性能。使用UniApp的条件编译功能,开发人员可以根据需要将代码划分为多个包。每个包都包含一组页面和组件࿰…...
)
JSON.stringify()
一、定义 JSON.stringify() 是一个 JavaScript 内置函数,用于将 JavaScript 对象或值转换为 JSON 字符串 二、语法 JSON.stringify(value, replacer, space); value:要转换为 JSON 字符串的 JavaScript 对象或值。 eplacer(可选࿰…...
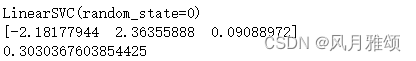
机器学习——损失函数
【说明】文章内容来自《机器学习——基于sklearn》,用于学习记录。若有争议联系删除。 1、简介 损失函数(loss function)又称为误差函数(error function),是衡量模型好坏的标准,用于估量模型的预测值与真实值的不一致程度,是一个…...
)
C#多线程(补充)
C#多线程(补充) C# 多线程的补充在C#中使用多线程1. Thread类2. 线程池3. Parallel类4. Task类启动任务接收任务的返回值同步调用指定连续任务任务的层次结构 5. BackgroundWorker控件 C# 多线程的补充 在C#中使用多线程 1. Thread类 使用Thread类通过…...
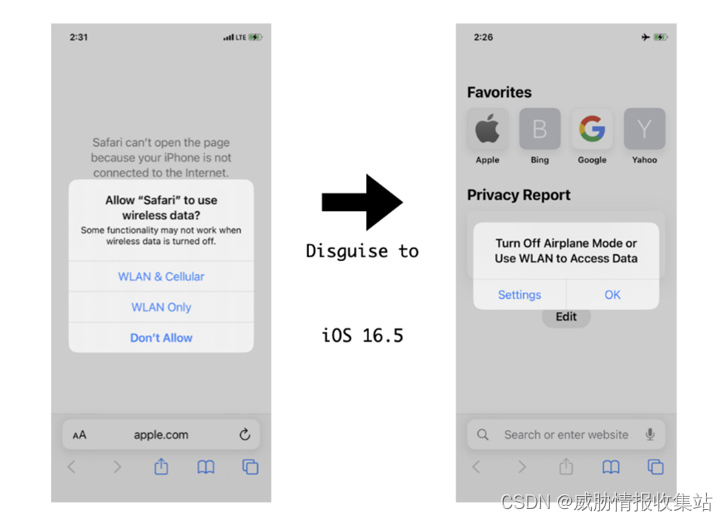
关于苹果iOS 16:揭开伪装成飞机模式的隐形蜂窝接入漏洞的动态情报
一、基本内容 在日常生活中,网络威胁不断演变,给个人和组织带来了一系列重大挑战。网络犯罪分子使用的一种最常见的、最具破坏性的方法之一就是网络钓鱼。这种攻击方式通过电子邮件、短信或其他通讯渠道冒充可信实体,诱使个人泄露敏感信息&am…...

Python+OpenCV 零基础学习笔记(4-5):计算机图形基础+Python相对文件路径+OpenCV图像+OpenCV视频
文章目录 相关链接运行环境前言计算机图形OpenCV简单使用图形读取文件读取可能会出现的问题:路径不对解决方案其它路径问题解决方案 图像显示保存OpenCV视频视频素材如何获取?简单视频读取 相关链接 【2022B站最好的OpenCV课程推荐】OpenCV从入门到实战 …...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...
