【论文阅读】Self-Paced Curriculum Learning
论文下载
代码
Supplementary Materials
bib:
@INPROCEEDINGS{,title = {Self-Paced Curriculum Learning},author = {Lu Jiang and Deyu Meng and Qian Zhao and Shiguang Shan and Alexander Hauptmann},booktitle = {AAAI},year = {2015},pages = {2694--2700}
}
1. 摘要
Curriculum learning (CL) or self-paced learning (SPL) represents a recently proposed learning regime inspired by the learning process of humans and animals that gradually proceeds from easy to more complex samples in training.
The two methods share a similar conceptual learning paradigm, but differ in specific learning schemes.
In CL, the curriculum is predetermined by prior knowledge, and remain fixed thereafter.
Therefore, this type of method heavily relies on the quality of prior knowledge while ignoring feedback about the learner.
In SPL, the curriculum is dynamically determined to adjust to the learning pace of the leaner.
However, SPL is unable to deal with prior knowledge, rendering it prone to overfitting.
In this paper, we discover the missing link between CL and SPL, and propose a unified framework named self-paced curriculum leaning (SPCL).
SPCL is formulated as a concise optimization problem that takes into account both prior knowledge known before training and the learning progress during training.
In comparison to human education, SPCL is analogous to “instructor-student-collaborative” learning mode, as opposed to “instructor-driven” in CL or “student-driven” in SPL.
Empirically, we show that the advantage of SPCL on two tasks.
课程学习(CL)或自定进度学习(SPL)代表了最近提出的一种学习制度,其灵感来自人类和动物的学习过程,在训练中逐渐从简单到更复杂的样本进行。 这两种方法具有相似的概念学习范式,但具体的学习方案有所不同。 在 CL 中,课程是由先验知识预先确定的,并且此后保持固定。 因此,这种方法严重依赖先验知识的质量,而忽略了学习者的反馈。 在 SPL 中,课程是动态确定的,以适应学习者的学习节奏。 然而,SPL 无法处理先验知识,因此容易出现过度拟合。 在本文中,我们发现了 CL 和 SPL 之间缺失的联系,并提出了一个名为自定进度课程学习(SPCL)的统一框架。 SPCL 被表述为一个简洁的优化问题,它考虑了训练前已知的先验知识和训练期间的学习进度。 与人类教育相比,SPCL类似于“师生协作”的学习模式,而不是CL中的“教师驱动”或SPL中的“学生驱动”。 根据经验,我们展示了 SPCL 在两项任务上的优势。
Note:
- 课程学习依赖于课程先验,在许多场景中,课程先验一般都是缺失的。这种方法严重依赖于先验知识的质量,而忽略了学习者的反馈,相当于是
老师主导。 - 自步学习中课程是动态确定的,以适应学习者节奏。其中,动态确定只是按照loss的高低当作是样本的难易,无法处理额外加入的知识先验。
2. 算法描述
2.1. 自步学习
min w , v ∈ [ 0 , 1 ] n E ( w , v ; λ ) = ∑ i = 1 n v i L ( y i , f ( x i , w ) ) − λ ∥ v ∥ 1 (1) \min_{\mathbf{w}, \mathbf{v} \in[0, 1]^n}\mathbb{E}(\mathbf{w}, \mathbf{v};\lambda) = \sum_{i=1}^n{v_iL(y_i, f(x_i,\mathbf{w}))} - \lambda\|\mathbf{v}\|_1 \tag{1} w,v∈[0,1]nminE(w,v;λ)=i=1∑nviL(yi,f(xi,w))−λ∥v∥1(1)
等式1应该就是自步学习中最经典的形式了。其中,对于自步正则 − ∥ v ∥ 1 -\|\mathbf{v}\|_1 −∥v∥1是可以替换的,有很多的类型,这个是最经典的hard型(非0即1)。对于等式1的求解可以采用ACS (Alternative Convex Search)。
- 固定 w \mathbf{w} w,求解 v \mathbf{v} v。存在闭式解 v ∗ = [ v 1 ∗ , … , v n ∗ ] \mathbf{v}^* = [v_1^*, \dots, v_n^*] v∗=[v1∗,…,vn∗],
v i ∗ = { 1 , L ( y i , f ( x i , w ) ) < λ ; 0 , otherwise. v_i^* = \begin{cases} 1, & L(y_i, f(x_i, \mathbf{w})) < \lambda;\\ 0, &\text{otherwise.}\\ \end{cases} vi∗={1,0,L(yi,f(xi,w))<λ;otherwise. - 固定 v \mathbf{v} v,用梯度下降法(也可以用其他优化方法)求解 w \mathbf{w} w。
存在的弊端:
However, since the learning is completely dominated by the
training loss, the learning may be prone to overfitting. Moreover, it provides no way to incorporate prior guidance in learning. To the best of our knowledge, there has been no studies to incorporate prior knowledge into SPL, nor to analyze the relation between CL and SPL.
2.1. 自步课程学习
自步课程学习想要打造一种师生协同的学习范式,其中,同时考虑训练前已知的先验知识和训练期间学到的知识。
Self-paced Curriculum Learning:
3. 实验
from scipy.optimize import minimize
import numpy as np# samples
id = np.array(['a', 'b', 'c', 'd', 'e', 'f'])
myloss = np.array([0.1, 0.2, 0.4, 0.6, 0.5, 0.3]).reshape([-1, 1])
print("####### input loss ######")
print(myloss)# 4) calculate curriculum constraints
# A = matrix(0, nrow=length(id), ncol=1)
# curriculum constraints matrix
A = np.zeros([len(id), 1])
A[:, 0] = np.array([0.1, 0.0, 0.4, 0.3, 0.5, 1.0])
# A[:, 0] = np.array([2.3, 2.2, 2.1, 2.0, 1.7, 1.5])
print("####### A matrix ######")
print("A: ", A)
c = 1.0
# c = 6.0# 5) optimize v with modality constraint (A)
# v0 = replicate(length(id),0)
v0 = np.repeat(0, len(id))
print("v0: ", v0)
# a small constant for optmization accuracy
tolerance = 1e-7
print("tolerance: ", tolerance)# tolerance = 0
# parameter in self-paced learning
lambda_var = 0.8333# paramaters
u1 = -1 * A # -Av >= -c i.e. Av <= c# c1 = -1 * c - tolerance # -Av >= -c i.e. Av <= c
c1 = c + tolerance# 三个约束
# v 大于等于 0
# v 小于等于 1
# A^T \times V <= c
# inequality means that it is to be non-negative.
cons = ({'type': 'ineq', 'fun': lambda v: v @ u1 + c1})# 定义目标函数
def objective_function(v):obj = v @ myloss - lambda_var * np.sum(v)return obj# 定义目标函数的梯度
def objective_gradient(v):grads = myloss - lambda_varreturn grads# 设置bounds
# bounds = tuple([(-tolerance, 1 + tolerance) for i in range(len(v0))])
bounds = tuple([(0, 1) for i in range(len(v0))])
# x0 = np.zeros([len(id)])
# res_SLSQP = minimize(objective_function, v0, method='SLSQP', jac=objective_gradient, constraints=cons, bounds=bounds)# res = minimize(objective_function, v0, method='SLSQP', constraints=cons, bounds=bounds)
print("###res_SLSQP###")
res_SLSQP = minimize(objective_function, v0, method='SLSQP', jac=objective_gradient, constraints=cons, bounds=bounds,options={"maxiter": 100, "disp": True})
print('最小值:', res_SLSQP.fun)
print('最优解:', res_SLSQP.x)
print('迭代终止是否成功:', res_SLSQP.success)
print('迭代终止原因:', res_SLSQP.message)
print("最终解是否满足先验课程知识: ", res_SLSQP.x @ u1 + c1 >= 0)print("###COBYLA###")
res_COBYLA = minimize(objective_function, v0, method='COBYLA', jac=objective_gradient, constraints=cons, bounds=bounds,options={"maxiter": 100, "disp": True})
print('最小值:', res_COBYLA.fun)
print('最优解:', res_COBYLA.x)
print('迭代终止是否成功:', res_COBYLA.success)
print('迭代终止原因:', res_COBYLA.message)
print("最终解是否满足先验课程知识: ", res_COBYLA.x @ u1 + c1 >= 0)# v_2 = np.array([1, 1, 1, 0.88, 0.47, 0])
v_2 = np.array([1, 0.91, 0.10, 0.00, 0.00, 1.00])
print('论文最优解:', v_2)
print("论文最小值:", objective_function(v_2))
print("论文最终解是否满足先验课程知识: ", v_2 @ u1 + c1 >= 0)相关文章:

【论文阅读】Self-Paced Curriculum Learning
论文下载 代码 Supplementary Materials bib: INPROCEEDINGS{,title {Self-Paced Curriculum Learning},author {Lu Jiang and Deyu Meng and Qian Zhao and Shiguang Shan and Alexander Hauptmann},booktitle {AAAI},year {2015},pages {2694--2700} }1. 摘…...

C++简易线程池
原理说明: 1. 线程池创建时,指定线程池的大小thread_size。当有新的函数任务通过函数addFunction ()添加进来后,其中一个线程执行函数。一个线程一次执行一个函数。如果函数数量大与线程池数量,则后来的函数等待。 2. 线程池内部…...
【MATLAB】PSO粒子群优化LSTM(PSO_LSTM)的时间序列预测
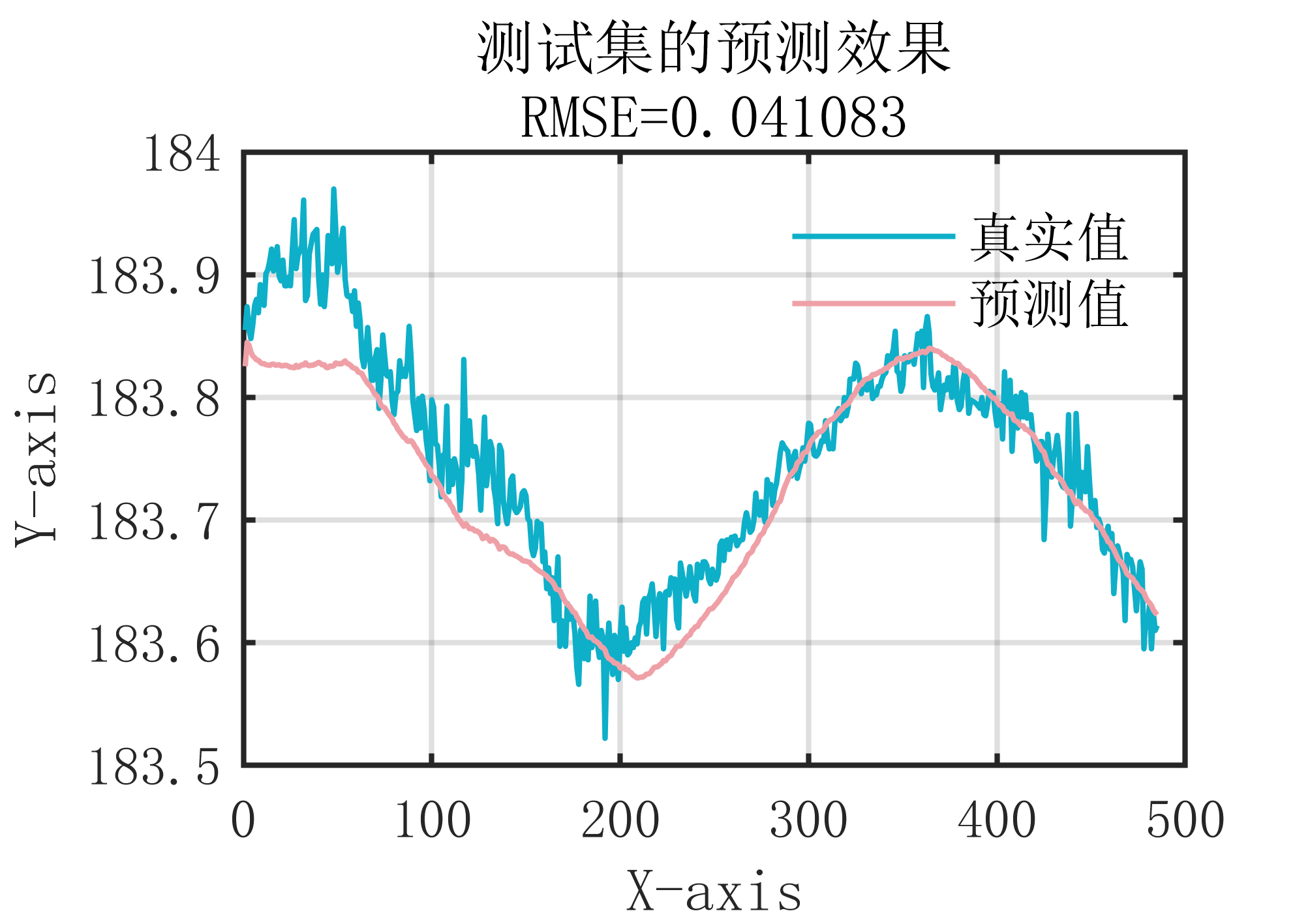
有意向获取代码,请转文末观看代码获取方式~也可转原文链接获取~ 1 基本定义 PSO粒子群优化LSTM(PSO-LSTM)是一种将粒子群优化算法(PSO)与长短期记忆神经网络(LSTM)相结合的混合模型。该算法通过…...
产品经理学习-怎么写PRD文档
目录 瀑布流方法论介绍 产品需求文档(PRD)介绍 产品需求文档的基本要素 撰写产品需求文档 优先产品需求文档的特点 其他相关文档 瀑布流方法论介绍 瀑布流模型是一种项目的开发和管理的方法论,是敏捷的开发管理方式相对应的另一种方法…...

第3课 获取并播放音频流
本课对应源文件下载链接: https://download.csdn.net/download/XiBuQiuChong/88680079 FFmpeg作为一套庞大的音视频处理开源工具,其源码有太多值得研究的地方。但对于大多数初学者而言,如何快速利用相关的API写出自己想要的东西才是迫切需要…...
Spark编程实验四:Spark Streaming编程
目录 一、目的与要求 二、实验内容 三、实验步骤 1、利用Spark Streaming对三种类型的基本数据源的数据进行处理 2、利用Spark Streaming对Kafka高级数据源的数据进行处理 3、完成DStream的两种有状态转换操作 4、把DStream的数据输出保存到文本文件或MySQL数据库中 四…...

Flink去重计数统计用户数
1.数据 订单表,分别是店铺id、用户id和支付金额 "店铺id,用户id,支付金额", "shop-1,user-1,1", "shop-1,user-2,1", "shop-1,user-2,1", "shop-1,user-3,1", "shop-1,user-3,1", "shop-1,user…...
力扣:62. 不同路径(动态规划,附python二维数组的定义)
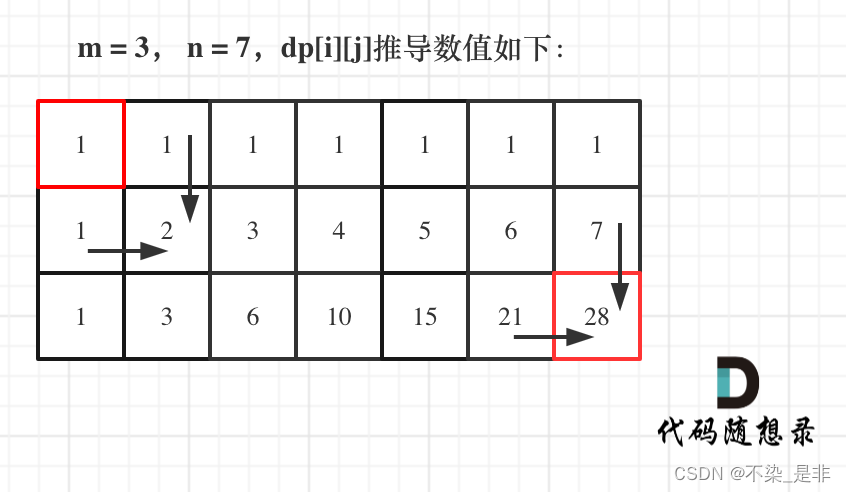
题目: 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。 问总共有多少条不同的路径&…...
2022年全球运维大会(GOPS深圳站)-核心PPT资料下载
一、峰会简介 GOPS 主要面向运维行业的中高端技术人员,包括运维、开发、测试、架构师等群体。目的在于帮助IT技术从业者系统学习了解相关知识体系,让创新技术推动社会进步。您将会看到国内外知名企业的相关技术案例,也能与国内顶尖的技术专家…...

8868体育助力意甲罗马俱乐部 迪巴拉有望付出
8868体育助力意甲罗马俱乐部 迪巴拉有望付出 意甲罗马俱乐部是8868体育合作球队之一,本赛季,在意甲第14轮的比赛中,罗马客场2-1战胜萨索洛,积分上升到意甲第4位。 有报道称,迪巴拉在对阵佛罗伦萨的比赛中受伤ÿ…...

java设计模式实战【策略模式+观察者模式+命令模式+组合模式,混合模式在支付系统中的应用】
引言 在代码开发的世界里,理论知识的重要性毋庸置疑,但实战经验往往才是知识的真正试金石。正所谓,“读万卷书不如行万里路”,理论的学习需要通过实践来验证和深化。设计模式作为软件开发中的重要理论,其真正的价值在…...

小程序wx:if 和hidden的区别?
在小程序中,wx:if 和 hidden 是用于条件渲染的两种不同方式。 选择使用哪种方式取决于具体情况。如果条件变化频繁或节点包含复杂的子节点,可以考虑使用 wx:if 进行条件渲染;如果条件变化较少且节点结构简单,可以使用 hidden 控制…...
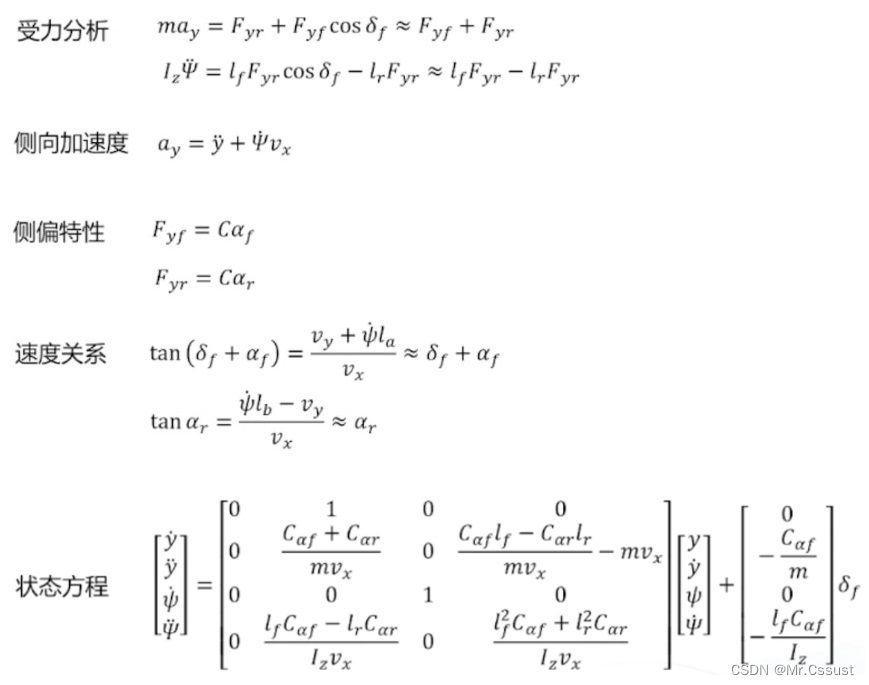
自动驾驶学习笔记(二十三)——车辆控制模型
#Apollo开发者# 学习课程的传送门如下,当您也准备学习自动驾驶时,可以和我一同前往: 《自动驾驶新人之旅》免费课程—> 传送门 《Apollo开放平台9.0专项技术公开课》免费报名—>传送门 文章目录 前言 运动学模型 动力学模型 总结…...

Linux Shell 015-文本双向覆盖重定向工具tee
Linux Shell 015-文本双向覆盖重定向工具tee 本节关键字:Linux、Bash Shell、文本双向覆盖重定向工具 相关指令:tee、echo、cat tee介绍 tee工具是从标准输入读取并写入到标准输出和文件,即:双向覆盖重定向(屏幕输出…...

【PyQt】(自定义类)QIcon派生,更易用的纯色Icon
嫌Qt自带的icon太丑,自己写了一个,主要用于纯色图标的自由改色。 当然,图标素材得网上找。 Qt原生图标与现代图标对比: 没有对比就没有伤害 Qt图标 网络素材图标 自定义类XJQ_Icon: from PyQt5.QtGui import QIc…...

【mysql】数据处理格式化、转换、判断
数据处理 判断是否超时,时间是否大于当前时间计算分钟数时间格式化处理如果数值类型进行转换字符类型字符拼接case-when代替if-else判断数据空(特殊:含空数据、空字符处理) select /*判断是否超时,时间是否大于当前…...

深入探索Java中的UDP网络通信机制
在网络通信中,UDP(User Datagram Protocol,用户数据报协议)是一种无连接的协议,它在某些情况下比TCP更适合,尤其是在要求速度快、对数据准确性要求相对较低的场景下。本文将介绍如何使用Java进行UDP网络通信…...

List常见方法和遍历操作
List集合的特点 有序: 存和取的元素顺序一致有索引:可以通过索引操作元素可重复:存储的元素可以重复 List集合的特有方法 Collection的方法List都继承了List集合因为有索引,所以有了很多操作索引的方法 ublic static void main…...
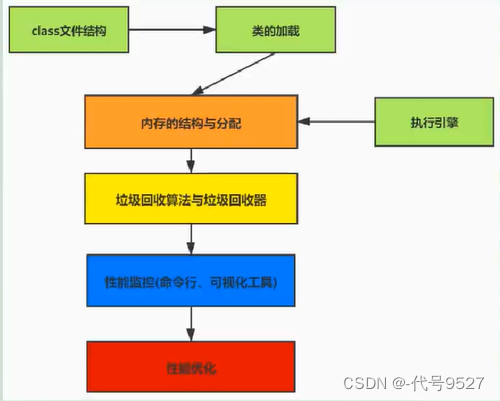
【基础篇】一、认识JVM
文章目录 1、虚拟机2、Java虚拟机3、JVM的整体结构4、Java代码的执行流程5、JVM的三大功能6、JVM的分类7、JVM的生命周期 1、虚拟机 虚拟机,Virtual Machine,一台虚拟的计算机,用来执行虚拟计算机指令。分为: 系统虚拟机&#x…...
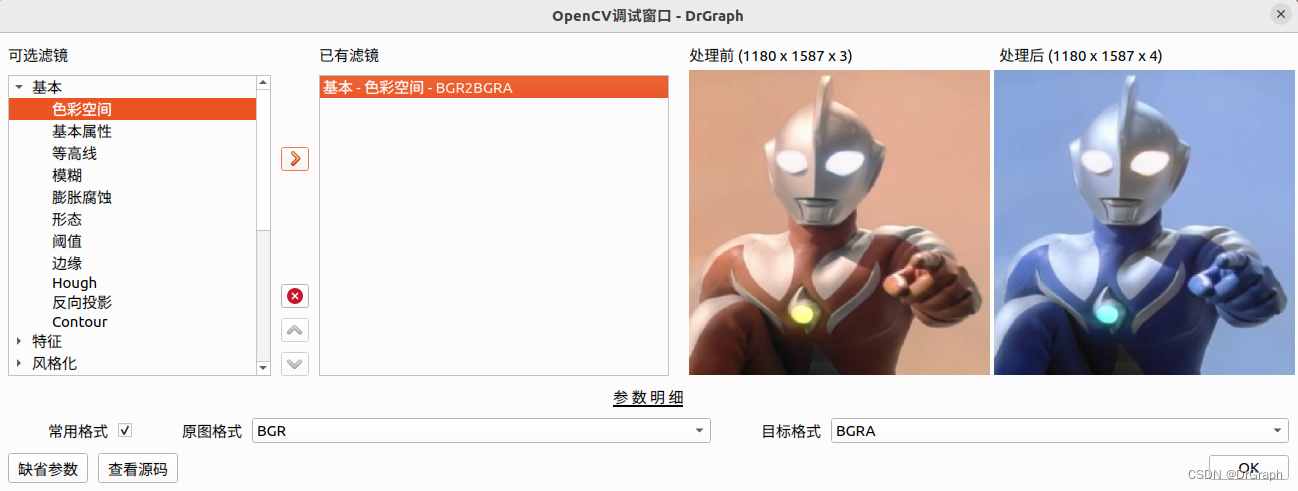
DrGraph原理示教 - OpenCV 4 功能 - 颜色空间
前言 前段时间,甲方提出明确需求,让把软件国产化。稍微研究了一下,那就转QT开发,顺便把以前的功能代码重写一遍。 至于在Ubuntu下折腾QT、OpenCV安装事宜,网上文章很多,照猫画虎即可。 这个过程࿰…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...
