模式识别与机器学习-SVM(线性支持向量机)
线性支持向量机
- 线性支持向量机
- 间隔距离
- 学习的对偶算法
- 算法:线性可分支持向量机学习算法
- 线性可分支持向量机例子
谨以此博客作为复习期间的记录
线性支持向量机
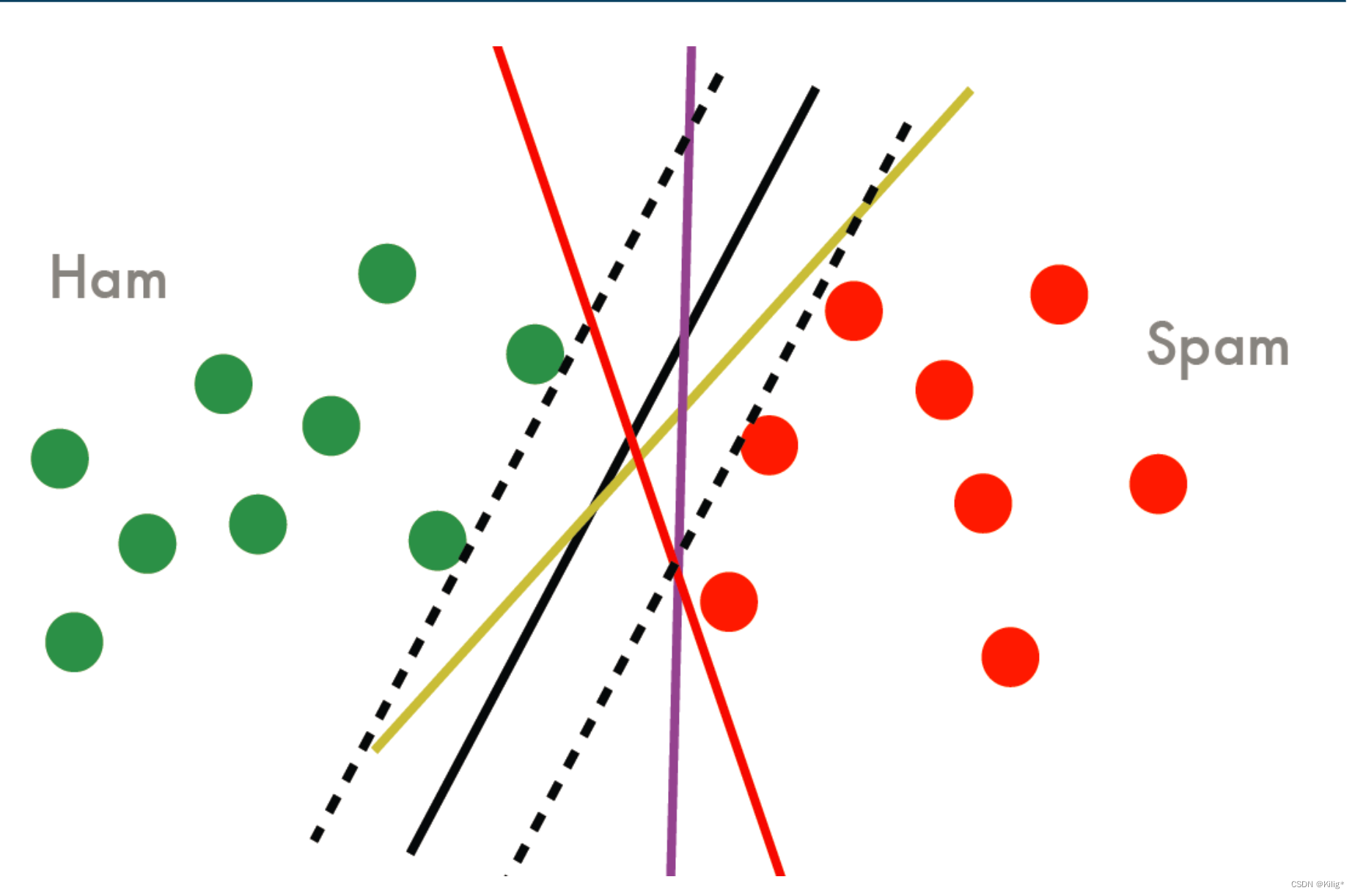
在以上四条线中,都可以作为分割平面,误差率也都为0。但是那个分割平面效果更好呢?其实可以看出,黑色的线具有更好的性质,因为如果将黑色的线作为分割平面,将会有更大的间隔距离。
其中,分割平面可以用以下式子表示:
w x + b = 0 wx+b = 0 wx+b=0
w 和 b w\text{和}b w和b都是有待学习的参数,SVM的核心思想之一就是找到这样的一个平面,使得间隔距离最大。那么该如何表述间隔距离呢?
间隔距离
在分割平面 w x + b = 0 wx+b = 0 wx+b=0确定的情况下,对每一个样本点 x i , ∣ w x i + b ∣ x_i,|wx_i+b| xi,∣wxi+b∣可以表示样本点 x i x_i xi到分割平面的距离。而若是二分类, y i ∈ { 1 , − 1 } y_i \in \{1,-1\} yi∈{1,−1},那么 y i ( w x i + b ) y_i(wx_i+b) yi(wxi+b)同样可以表示样本点到分割平面的距离。
对于二分类问题,数据点 x i \mathbf{x}_i xi 到超平面的函数间隔定义为: γ ^ i = y i ( w ⋅ x i + b ) \hat{\gamma}_i = y_i (\mathbf{w} \cdot \mathbf{x}_i + b) γ^i=yi(w⋅xi+b)
函数间隔的正负号表示数据点所属的类别和超平面分割的一致性。当 γ ^ i > 0 \hat{\gamma}_i > 0 γ^i>0 时,数据点 x i \mathbf{x}_i xi 被正确地分类到超平面两侧的区域,而当 γ ^ i < 0 \hat{\gamma}_i < 0 γ^i<0 时,数据点被错误地分类或位于超平面上。若 γ ^ i = 0 \hat{\gamma}_i = 0 γ^i=0,则表示数据点在超平面上。
而这里就可以得出SVM的初步思想:最大化最小函数间隔,公式表述如下
m a x m i n ( γ ^ i ) i = 1... N max \quad min(\hat{\gamma}_i) \qquad i = 1...N maxmin(γ^i)i=1...N
也就是在所有样本点 ( x i , y i ) (x_i,y_i) (xi,yi)中,可以找到离分割平面最近的点,我们想让这些点的距离达到最大。但是有一个问题,但是选择分离超平面时,只有函数间隔还不够.因为只要成比例地改变 w w w和 b b b ,例如将它们改为 2 w 2w 2w 和 2 b 2b 2b ,超平面并没有改变,但函数间隔却成为原来的 2 倍.这一事实启示我们,可以对分离超平面的法向量 w w w 加某些约束,如规范化 ∣ ∣ w ∣ ∣ = 1 ||w|| = 1 ∣∣w∣∣=1,这时函数间隔就变为了几何间隔。
几何间隔 对于给定的训练数据集 T T T 和超平面 ( w , b ) (w, b) (w,b), 定义超平面 ( w , b ) (w, b) (w,b) 关于样本点 ( x i , y i ) \left(x_i, y_i\right) (xi,yi) 的几何间隔为
γ i = y i ( w ∥ w ∥ ⋅ x i + b ∥ w ∥ ) \gamma_i=y_i\left(\frac{w}{\|w\|} \cdot x_i+\frac{b}{\|w\|}\right) γi=yi(∥w∥w⋅xi+∥w∥b)
定义超平面 ( w , b ) (w, b) (w,b) 关于训练数据集 T T T 的几何间隔为超平面 ( w , b ) (w, b) (w,b) 关于 T T T 中所有样本点 ( x i , y i ) \left(x_i, y_i\right) (xi,yi) 的几何间隔之最小值, 即
γ = min i = 1 , ⋯ , N γ i \gamma=\min _{i=1, \cdots, N} \gamma_i γ=i=1,⋯,Nminγi
超平面 ( w , b ) (w, b) (w,b) 关于样本点 ( x i , y i ) \left(x_i, y_i\right) (xi,yi) 的几何间隔一般是实例点到超平面的带符号的距离 (signed distance), 当样本点被超平面正确分类时就是实例点到超平面的距离.
从函数间隔和几何间隔的定义 (式(7.3) 式(7.6))可知, 函数间隔和几何间隔有下面的关系:
γ i = γ ^ i ∥ w ∥ γ = γ ^ ∥ w ∥ \begin{gathered} \gamma_i=\frac{\hat{\gamma}_i}{\|w\|} \\ \gamma=\frac{\hat{\gamma}}{\|w\|} \end{gathered} γi=∥w∥γ^iγ=∥w∥γ^
如果 ∥ w ∥ = 1 \|w\|=1 ∥w∥=1, 那么函数间隔和几何间隔相等. 如果超平面参数 w w w 和 b b b 成比例地改变 (超平面没有改变),函数间隔也按此比例改变,而几何间隔不变.
那么,优化目标可以等价的表述如下
maximize γ subject to γ ≤ y i ( w ∥ w ∥ ⋅ x i + b ∥ w ∥ ) , i = 1 , 2 , … , n \begin{align*} & \text{maximize} \quad \gamma \\ & \text{subject to} \quad \gamma \leq y_i \left(\frac{\mathbf{w}}{\|\mathbf{w}\|} \cdot \mathbf{x}_i + \frac{b}{\|\mathbf{w}\|}\right), \quad i = 1, 2, \dots, n \end{align*} maximizeγsubject toγ≤yi(∥w∥w⋅xi+∥w∥b),i=1,2,…,n
转化为几何间隔:
maximize γ ^ ∥ w ∥ subject to γ ^ ≤ y i ( w ⋅ x i + b ) , i = 1 , 2 , … , n \begin{align*} & \text{maximize} \quad \frac{\hat{\gamma}}{\|w\|} \\ & \text{subject to} \quad \hat{\gamma} \leq y_i \left(\mathbf{w} \cdot \mathbf{x}_i + b\right), \quad i = 1, 2, \dots, n \end{align*} maximize∥w∥γ^subject toγ^≤yi(w⋅xi+b),i=1,2,…,n
可以令 γ ^ = 1 \hat{\gamma} = 1 γ^=1,目标函数变为 m a x i m i z e 1 ∣ ∣ w ∣ ∣ maximize \quad\frac{1}{||w||} maximize∣∣w∣∣1,等价于 m i n i m i z e 1 2 ∣ ∣ w ∣ ∣ minimize\quad \frac{1}{2}||w|| minimize21∣∣w∣∣.原问题可化为以下形式.
minimize 1 2 ∣ ∣ w ∣ ∣ 2 subject to y i ( w ⋅ x i + b ) − 1 ≥ 0 , i = 1 , 2 , … , n \begin{align*} & \text{minimize} \quad \frac{1}{2}||w||^2\\ & \text{subject to} \quad y_i \left(\mathbf{w} \cdot \mathbf{x}_i + b\right) - 1\geq 0, \quad i = 1, 2, \dots, n \end{align*} minimize21∣∣w∣∣2subject toyi(w⋅xi+b)−1≥0,i=1,2,…,n
以上是一个凸优化问题,通过求解上述问题即可得到最终的最优决策平面。

在决定分离超平面时只有支持向量起作用,而其他实例点并不起作用.如果移动支持向量将改变所求的解;但是如果在间隔边界以外移动其他实例点,甚至去掉这些点,则解是不会改变的.由于支持向量在确定分离超平面中起着决定性作用,所以将这种分类模型称为支持向量机.支持向量的个数一般很少,所以支持向量机由很少的“重要的”训练样本确定.
学习的对偶算法
为了求解上述问题,可以构造拉格朗日函数,通过求解对偶问题得到原始问题的最优解。
这样做的优点,一是对偶问题往往更容易求解;二是自然引入核函数,进而推广到非线性分类问题。
首先构建拉格朗日函数 (Lagrange function). 为此, 对每一个不等式约束引进拉格朗日乘子 (Lagrange multiplier) α i ⩾ 0 , i = 1 , 2 , ⋯ , N \alpha_i \geqslant 0, i=1,2, \cdots, N αi⩾0,i=1,2,⋯,N, 定义拉格朗日函数:
L ( w , b , α ) = 1 2 ∥ w ∥ 2 − ∑ i = 1 N α i y i ( w ⋅ x i + b ) + ∑ i = 1 N α i L(w, b, \alpha)=\frac{1}{2}\|w\|^2-\sum_{i=1}^N \alpha_i y_i\left(w \cdot x_i+b\right)+\sum_{i=1}^N \alpha_i L(w,b,α)=21∥w∥2−i=1∑Nαiyi(w⋅xi+b)+i=1∑Nαi
其中, α = ( α 1 , α 2 , ⋯ , α N ) T \alpha=\left(\alpha_1, \alpha_2, \cdots, \alpha_N\right)^{\mathrm{T}} α=(α1,α2,⋯,αN)T 为拉格朗日乘子向量.
根据拉格朗日对偶性,原始问题的对偶问题是极大极小问题:
max α min w , b L ( w , b , α ) \max _\alpha \min _{w, b} L(w, b, \alpha) αmaxw,bminL(w,b,α)
所以, 为了得到对偶问题的解, 需要先求 L ( w , b , α ) L(w, b, \alpha) L(w,b,α) 对 w , b w, b w,b 的极小, 再求对 α \alpha α 的极大.
拉格朗日函数为:
L ( w , b , α ) = 1 2 ∥ w ∥ 2 − ∑ i = 1 N α i y i ( w ⋅ x i + b ) + ∑ i = 1 N α i L(w, b, \alpha)=\frac{1}{2}\|\mathbf{w}\|^2-\sum_{i=1}^N \alpha_i y_i(\mathbf{w} \cdot \mathbf{x}_i+b)+\sum_{i=1}^N \alpha_i L(w,b,α)=21∥w∥2−i=1∑Nαiyi(w⋅xi+b)+i=1∑Nαi
其中, α = ( α 1 , α 2 , ⋯ , α N ) T \alpha=\left(\alpha_1, \alpha_2, \cdots, \alpha_N\right)^{\mathrm{T}} α=(α1,α2,⋯,αN)T 为拉格朗日乘子向量。
接下来,我们进行极小化 L ( w , b , α ) L(w, b, \alpha) L(w,b,α) 对 w w w 和 b b b的过程。需要对 L ( w , b , α ) L(w, b, \alpha) L(w,b,α) 分别对 w w w 和 b b b 求偏导,并令其等于零:
对 w w w 的偏导数:
∂ L ∂ w = w − ∑ i = 1 N α i y i x i = 0 \frac{\partial L}{\partial w} = w - \sum_{i=1}^N \alpha_i y_i x_i = 0 ∂w∂L=w−∑i=1Nαiyixi=0
得到: w = ∑ i = 1 N α i y i x i w = \sum_{i=1}^N \alpha_i y_i x_i w=∑i=1Nαiyixi
对 b b b 的偏导数:
∂ L ∂ b = − ∑ i = 1 N α i y i = 0 \frac{\partial L}{\partial b} = -\sum_{i=1}^N \alpha_i y_i = 0 ∂b∂L=−∑i=1Nαiyi=0
得到: ∑ i = 1 N α i y i = 0 \sum_{i=1}^N \alpha_i y_i = 0 ∑i=1Nαiyi=0
将上述对 w w w 和 b b b 的结果代入拉格朗日函数 L ( w , b , α ) L(w, b, \alpha) L(w,b,α),得到极小化后的结果
这样,对偶问题可以表示为:
min α − 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) + ∑ i = 1 N α i \min_\alpha -\frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j (x_i \cdot x_j) + \sum_{i=1}^N \alpha_i αmin−21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)+i=1∑Nαi
其中, α i ⩾ 0 \alpha_i \geqslant 0 αi⩾0, i = 1 , 2 , ⋯ , N i=1, 2, \cdots, N i=1,2,⋯,N,并且满足 ∑ i = 1 N α i y i = 0 \sum_{i=1}^N \alpha_i y_i = 0 ∑i=1Nαiyi=0。
然后,对拉格朗日函数 L ( w , b , α ) L(w, b, \alpha) L(w,b,α) 对 α \alpha α 求极大值,这样就可以得到对偶问题的解。
那么求解得到 α \alpha α之后,该如何反求出 w ∗ , b ∗ w^*,b^* w∗,b∗呢?
根据KKT条件,有
∇ w L ( w ∗ , b ∗ , α ∗ ) = w ∗ − ∑ i = 1 N α i ∗ y i x i = 0 ∇ b L ( w ∗ , b ∗ , α ∗ ) = − ∑ i = 1 N α i ∗ y i = 0 α i ∗ ( y i ( w ∗ ⋅ x i + b ∗ ) − 1 ) = 0 , i = 1 , 2 , ⋯ , N y i ( w ∗ ⋅ x i + b ∗ ) − 1 ⩾ 0 , i = 1 , 2 , ⋯ , N α i ∗ ⩾ 0 , i = 1 , 2 , ⋯ , N \begin{aligned} & \nabla_w L\left(w^*, b^*, \alpha^*\right)=w^*-\sum_{i=1}^N \alpha_i^* y_i x_i=0 \\ & \nabla_b L\left(w^*, b^*, \alpha^*\right)=-\sum_{i=1}^N \alpha_i^* y_i=0 \\ & \alpha_i^*\left(y_i\left(w^* \cdot x_i+b^*\right)-1\right)=0, \quad i=1,2, \cdots, N \\ & y_i\left(w^* \cdot x_i+b^*\right)-1 \geqslant 0, \quad i=1,2, \cdots, N \\ & \alpha_i^* \geqslant 0, \quad i=1,2, \cdots, N \end{aligned} ∇wL(w∗,b∗,α∗)=w∗−i=1∑Nαi∗yixi=0∇bL(w∗,b∗,α∗)=−i=1∑Nαi∗yi=0αi∗(yi(w∗⋅xi+b∗)−1)=0,i=1,2,⋯,Nyi(w∗⋅xi+b∗)−1⩾0,i=1,2,⋯,Nαi∗⩾0,i=1,2,⋯,N
由此得
w ∗ = ∑ i α i ∗ y i x i w^*=\sum_i \alpha_i^* y_i x_i w∗=i∑αi∗yixi
其中至少有一个 α j ∗ > 0 \alpha_j^*>0 αj∗>0 (用反证法, 假设 α ∗ = 0 \alpha^*=0 α∗=0, 由第一条KKT条件可知 w ∗ = 0 w^*=0 w∗=0, 而 w ∗ = 0 w^*=0 w∗=0不是原始最优化问题的解, 产生矛盾), 对此 j j j 有
y j ( w ∗ ⋅ x j + b ∗ ) − 1 = 0 y_j\left(w^* \cdot x_j+b^*\right)-1=0 yj(w∗⋅xj+b∗)−1=0
有 y j 2 = 1 y_j^2 = 1 yj2=1, y j ( w ∗ ⋅ x j + b ∗ ) − y j 2 = 0 y_j\left(w^* \cdot x_j+b^*\right)-y_j^2=0 yj(w∗⋅xj+b∗)−yj2=0进而得出 w ∗ ⋅ x j + b ∗ − y j = 0 w^* \cdot x_j+b^* - y_j = 0 w∗⋅xj+b∗−yj=0
因此,在求解出 α ∗ \alpha^* α∗之后,可以得到决策平面的 w ∗ 和 b ∗ w^*和b^* w∗和b∗
w ∗ = ∑ i α i ∗ y i x i b ∗ = y j − w ∗ ⋅ x j w^*=\sum_i \alpha_i^* y_i x_i\\ b^* = y_j - w^* \cdot x_j w∗=i∑αi∗yixib∗=yj−w∗⋅xj
算法:线性可分支持向量机学习算法
输入: 线性可分训练集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } T=\left\{\left(x_1, y_1\right),\left(x_2, y_2\right), \cdots,\left(x_N, y_N\right)\right\} T={(x1,y1),(x2,y2),⋯,(xN,yN)}, 其中 x i ∈ X = R n , y i ∈ x_i \in \mathcal{X}=\mathbf{R}^n, y_i \in xi∈X=Rn,yi∈ Y = { − 1 , + 1 } , i = 1 , 2 , ⋯ , N \mathcal{Y}=\{-1,+1\}, \quad i=1,2, \cdots, N Y={−1,+1},i=1,2,⋯,N;
输出: 分离超平面和分类决策函数.
(1)构造并求解约束最优化问题
min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i s.t. ∑ i = 1 N α i y i = 0 α i ⩾ 0 , i = 1 , 2 , ⋯ , N \begin{aligned} & \min _\alpha \quad \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j\left(x_i \cdot x_j\right)-\sum_{i=1}^N \alpha_i \\ & \text { s.t. } \quad \sum_{i=1}^N \alpha_i y_i=0 \\ & \alpha_i \geqslant 0, \quad i=1,2, \cdots, N \end{aligned} αmin21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−i=1∑Nαi s.t. i=1∑Nαiyi=0αi⩾0,i=1,2,⋯,N
求得最优解 α ∗ = ( α 1 ∗ , α 2 ∗ , ⋯ , α N ∗ ) T \alpha^*=\left(\alpha_1^*, \alpha_2^*, \cdots, \alpha_N^*\right)^{\mathrm{T}} α∗=(α1∗,α2∗,⋯,αN∗)T.
(2) 计算
w ∗ = ∑ i = 1 N α i ∗ y i x i w^*=\sum_{i=1}^N \alpha_i^* y_i x_i w∗=i=1∑Nαi∗yixi
并选择 α ∗ \alpha^* α∗ 的一个正分量 α j ∗ > 0 \alpha_j^*>0 αj∗>0, 计算
b ∗ = y j − ∑ i = 1 N α i ∗ y i ( x i ⋅ x j ) b^*=y_j-\sum_{i=1}^N \alpha_i^* y_i\left(x_i \cdot x_j\right) b∗=yj−i=1∑Nαi∗yi(xi⋅xj)
(3) 求得分离超平面
w ∗ ⋅ x + b ∗ = 0 w^* \cdot x+b^*=0 w∗⋅x+b∗=0
分类决策函数:
f ( x ) = sign ( w ∗ ⋅ x + b ∗ ) f(x)=\operatorname{sign}\left(w^* \cdot x+b^*\right) f(x)=sign(w∗⋅x+b∗)
在线性可分支持向量机中, w ∗ w^* w∗ 和 b ∗ b^* b∗ 只依赖于训练数据中对应于 α i ∗ > 0 \alpha_i^*>0 αi∗>0 的样本点 ( x i , y i ) \left(x_i, y_i\right) (xi,yi), 而其他样本点对 w ∗ w^* w∗ 和 b ∗ b^* b∗ 没有影响. 我们将训练数据中对应于 α i ∗ > 0 \alpha_i^*>0 αi∗>0 的实例点 x i ∈ R n x_i \in \mathbf{R}^n xi∈Rn 称为支持向量.
线性可分支持向量机例子

带入
min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i s.t. ∑ i = 1 N α i y i = 0 α i ⩾ 0 , i = 1 , 2 , ⋯ , N \begin{aligned} & \min _\alpha \quad \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j\left(x_i \cdot x_j\right)-\sum_{i=1}^N \alpha_i \\ & \text { s.t. } \quad \sum_{i=1}^N \alpha_i y_i=0 \\ & \alpha_i \geqslant 0, \quad i=1,2, \cdots, N \end{aligned} αmin21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−i=1∑Nαi s.t. i=1∑Nαiyi=0αi⩾0,i=1,2,⋯,N
解 根据所给数据, 对偶问题是
min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i = 1 2 ( 18 α 1 2 + 25 α 2 2 + 2 α 3 2 + 42 α 1 α 2 − 12 α 1 α 3 − 14 α 2 α 3 ) − α 1 − α 2 − α 3 s.t. α 1 + α 2 − α 3 = 0 α i ⩾ 0 , i = 1 , 2 , 3 \begin{array}{ll} \min _\alpha & \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j\left(x_i \cdot x_j\right)-\sum_{i=1}^N \alpha_i \\ & =\frac{1}{2}\left(18 \alpha_1^2+25 \alpha_2^2+2 \alpha_3^2+42 \alpha_1 \alpha_2-12 \alpha_1 \alpha_3-14 \alpha_2 \alpha_3\right)-\alpha_1-\alpha_2-\alpha_3 \\ \text { s.t. } & \alpha_1+\alpha_2-\alpha_3=0 \\ & \alpha_i \geqslant 0, \quad i=1,2,3 \end{array} minα s.t. 21∑i=1N∑j=1Nαiαjyiyj(xi⋅xj)−∑i=1Nαi=21(18α12+25α22+2α32+42α1α2−12α1α3−14α2α3)−α1−α2−α3α1+α2−α3=0αi⩾0,i=1,2,3
解这一最优化问题. 将 α 3 = α 1 + α 2 \alpha_3=\alpha_1+\alpha_2 α3=α1+α2 代入目标函数并记为
s ( α 1 , α 2 ) = 4 α 1 2 + 13 2 α 2 2 + 10 α 1 α 2 − 2 α 1 − 2 α 2 s\left(\alpha_1, \alpha_2\right)=4 \alpha_1^2+\frac{13}{2} \alpha_2^2+10 \alpha_1 \alpha_2-2 \alpha_1-2 \alpha_2 s(α1,α2)=4α12+213α22+10α1α2−2α1−2α2
对 α 1 , α 2 \alpha_1, \alpha_2 α1,α2 求偏导数并令其为 0 , 易知 s ( α 1 , α 2 ) s\left(\alpha_1, \alpha_2\right) s(α1,α2) 在点 ( 3 2 , − 1 ) T \left(\frac{3}{2},-1\right)^{\mathrm{T}} (23,−1)T 取极值, 但该点不满足约束条件 α 2 ⩾ 0 \alpha_2 \geqslant 0 α2⩾0, 所以最小值应在边界上达到.
当 α 1 = 0 \alpha_1=0 α1=0 时, 最小值 s ( 0 , 2 13 ) = − 2 13 s\left(0, \frac{2}{13}\right)=-\frac{2}{13} s(0,132)=−132; 当 α 2 = 0 \alpha_2=0 α2=0 时, 最小值 s ( 1 4 , 0 ) = − 1 4 s\left(\frac{1}{4}, 0\right)=-\frac{1}{4} s(41,0)=−41. 于是 s ( α 1 , α 2 ) s\left(\alpha_1, \alpha_2\right) s(α1,α2) 在 α 1 = 1 4 , α 2 = 0 \alpha_1=\frac{1}{4}, \alpha_2=0 α1=41,α2=0 达到最小, 此时 α 3 = α 1 + α 2 = 1 4 \alpha_3=\alpha_1+\alpha_2=\frac{1}{4} α3=α1+α2=41.
这样, α 1 ∗ = α 3 ∗ = 1 4 \alpha_1^*=\alpha_3^*=\frac{1}{4} α1∗=α3∗=41 对应的实例点 x 1 , x 3 x_1, x_3 x1,x3 是支持向量. 计算得
w 1 ∗ = w 2 ∗ = 1 2 b ∗ = − 2 \begin{gathered} w_1^*=w_2^*=\frac{1}{2} \\ b^*=-2 \end{gathered} w1∗=w2∗=21b∗=−2
分离超平面为
1 2 x ( 1 ) + 1 2 x ( 2 ) − 2 = 0 \frac{1}{2} x^{(1)}+\frac{1}{2} x^{(2)}-2=0 21x(1)+21x(2)−2=0
分类决策函数为
f ( x ) = sign ( 1 2 x ( 1 ) + 1 2 x ( 2 ) − 2 ) f(x)=\operatorname{sign}\left(\frac{1}{2} x^{(1)}+\frac{1}{2} x^{(2)}-2\right) f(x)=sign(21x(1)+21x(2)−2)
相关文章:

模式识别与机器学习-SVM(线性支持向量机)
线性支持向量机 线性支持向量机间隔距离学习的对偶算法算法:线性可分支持向量机学习算法线性可分支持向量机例子 谨以此博客作为复习期间的记录 线性支持向量机 在以上四条线中,都可以作为分割平面,误差率也都为0。但是那个分割平面效果更好呢࿱…...
【并行计算】GPU,CUDA
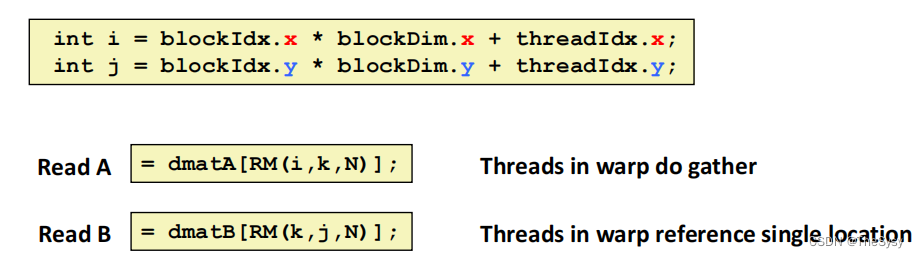
一、CUDA层次结构 1.kernel核函数 一个CUDA程序是一个kernel核函数被GPU的多个计算单元并行执行的过程,CUDA给了如下抽象 dim3 threadsPerBlock(4, 3, 1); dim3 numBlocks(3, 2, 1); matrixAdd<<<numBlocks, threadsPerBlock>>>(A, B, C); 2.G…...

计算机网络教案——计算机网络设备章节
第五章 计算机网络设备 一、教学目标: 1. 了解计算机网络的主要设备 2. 了解计算机网络设备的主要原理 3. 掌握计算机网络设备的基本用途 4. 掌握计算机网络设备的使用常识 二、教学重点、难点 计算机网络设备的主要原理 三、技能培训重点、难点 计算机网络设备的使用…...

什么是SLAM中的回环检测,如果没有回环检测会怎样
目录 什么是回环检测 如果没有回环检测 SLAM(Simultaneous Localization and Mapping,即同时定位与地图构建)是一种使机器人或自动驾驶汽车能够在未知环境中建立地图的同时定位自身位置的技术。回环检测(Loop Closure Detectio…...

ubuntu 通过文件设置静态IP、DNS、网关
1. 确定网络接口名称 首先,使用 ip a 命令确定您要配置的网络接口名称。 2. 编辑 Netplan 配置文件 使用文本编辑器(如 nano)打开或创建 Netplan 配置文件: sudo nano /etc/netplan/01-netcfg.yaml3. 输入 Netplan 配置 在编…...
mapboxgl 中热力图的实现以及给热力图点增加鼠标移上 popup 效果
文章目录 概要效果预览技术思路技术细节小结 概要 本篇文章还是关于最近做到的 mapboxgl 地图展开的。 借鉴官方示例:https://iclient.supermap.io/examples/mapboxgl/editor.html#heatMapLayer 效果预览 技术思路 将接口数据渲染到地图中形成热力图。还需要将热…...
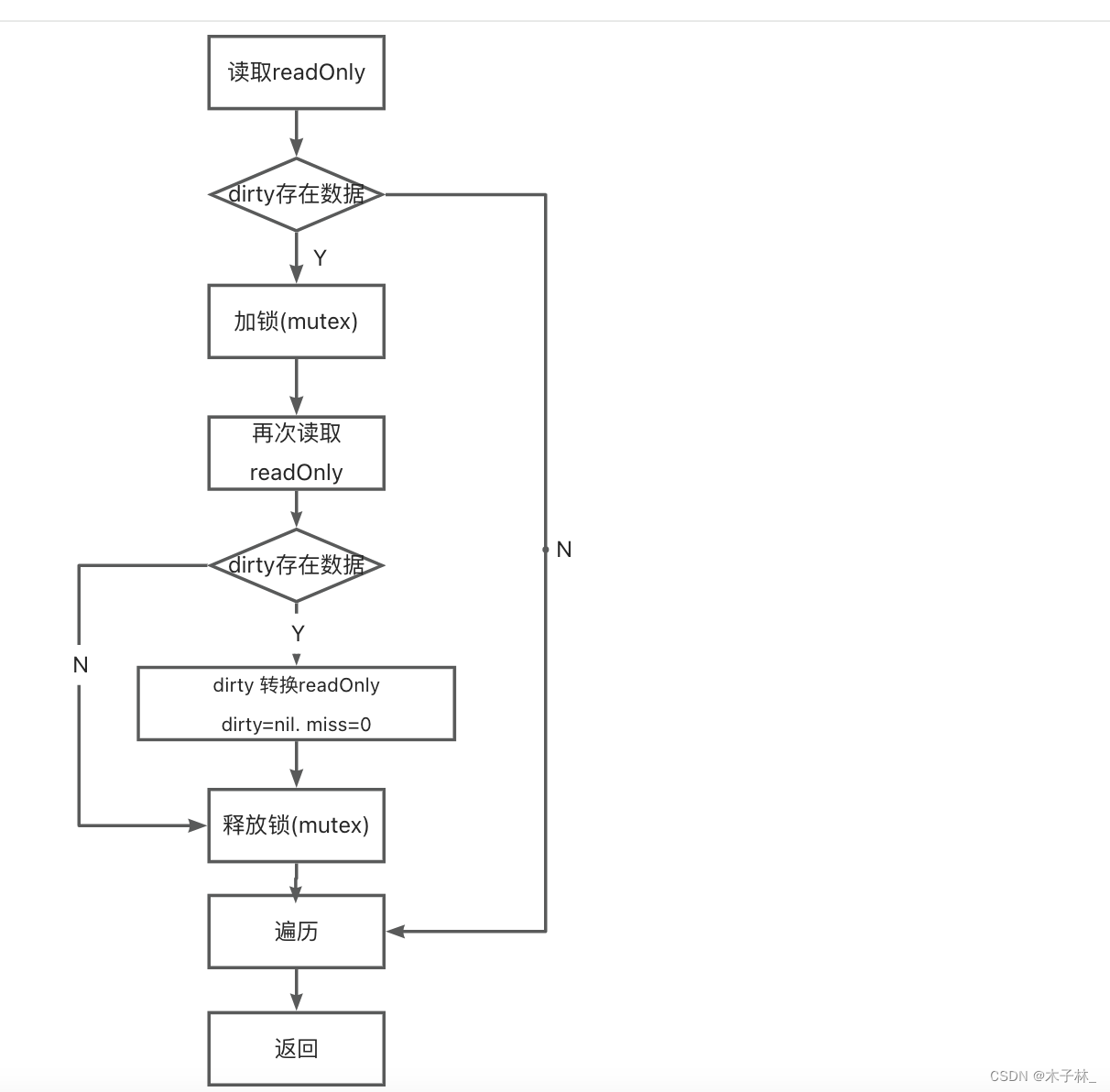
golang并发安全-sync.map
sync.map解决的问题 golang 原生map是存在并发读写的问题,在并发读写时候会抛出异常 func main() {mT : make(map[int]int)g1 : []int{1, 2, 3, 4, 5, 6}g2 : []int{4, 5, 6, 7, 8, 9}go func() {for i : range g1 {mT[i] i}}()go func() {for i : range g2 {mT[…...

开发第一个SpringBoot程序
使用命令创建Maven工程 mvn archetype:generate -DgroupIdorg.sang -DartifactIdchapter01 -DarchetypeArtifactIdmaven-archetype-quickstart -DinteractiveModefalse 参数说明: -DgroupId 组织Id(项目包名) -DartifactId 项目名称或模块…...

2023年度总结—你是你的年度MVP吗?
这段年度总结其实我之前就想写了,大概就是市赛比完之后18号的样子把,但是因为太懒了就一直拖到了现在哈哈,我思来想去,翻来覆去,彻夜难眠,想了想,还是决定把它写了吧!毕竟࿰…...

Linux基础知识学习3
vim编辑器 其分为四种模式 1.普通(命令)模式 2.编辑模式 3.底栏模式 4.可视化模式 vim编辑器被称为编辑器之神,而Emacs更是神之编辑器 普通模式: 1.光标移动 ^ 移动到行首 w 跳到下一个单词的开头…...
)
Leetcode5-在长度2N的数组中找出重复N次的元素(961)
1、题目 给你一个整数数组 nums ,该数组具有以下属性: nums.length 2 * n. nums 包含 n 1 个 不同的 元素 nums 中恰有一个元素重复 n 次 找出并返回重复了 n 次的那个元素。 示例 1: 输入:nums [1,2,3,3] 输出:…...

openssl的 openssl.cnf配置文件详解
背景:在上一篇文中,提到要写一篇openssl 配置文件详解的,这就来了~~~ find / -name openssl.cnf /etc/pki/tls/openssl.cnf /etc/pki/tls/openssl.cnf,该文件主要设置了证书请求、签名、crl相关的配置。主要相关的伪命令为ca和req…...
SpringBoot集成支付宝,看这一篇就够了。
前 言 在开始集成支付宝支付之前,我们需要准备一个支付宝商家账户,如果是个人开发者,可以通过注册公司或者让有公司资质的单位进行授权,后续在集成相关API的时候需要提供这些信息。 下面我以电脑网页端在线支付为例,介…...
数据结构程序设计——哈希表的应用(2)->哈希表解决冲突的方法
目录 实验须知 代码实现 实验报告 一:问题分析 二、数据结构 1.逻辑结构 2.物理结构 三、算法 (一)主要算法描述 1.用除留余数法构造哈希函数 2.线性探测再散列法 (一)主要算法实现代码 四、上机调试 实…...
微信小程序开发系列-07组件
微信小程序开发系列目录 《微信小程序开发系列-01创建一个最小的小程序项目》《微信小程序开发系列-02注册小程序》《微信小程序开发系列-03全局配置中的“window”和“tabBar”》《微信小程序开发系列-04获取用户图像和昵称》《微信小程序开发系列-05登录小程序》《微信小程序…...

JavaScript 中 Set 和 Map 的区别
JavaScript 中的 Set 和 Map 都是用来存储数据的数据结构,它们之间的区别如下: Set 是一组唯一值的集合,而 Map 是一组键值对的集合。Set 中的值是唯一的,不允许重复;Map 中的键是唯一的,值可以重复。Set …...

web前端之JavaScript
MENU JavaScript之设计模式、单例、代理、装饰者、中介者、观察者、发布订阅、策略JavaScript之数组静态方法的实现、reduce、forEach、map、push、every JavaScript之设计模式、单例、代理、装饰者、中介者、观察者、发布订阅、策略 单例模式 概念 保证一个类仅有一个实例&am…...
C# 图标标注小工具-查看重复文件
目录 效果 项目 代码 下载 效果 项目 代码 using System; using System.Collections.Generic; using System.Data; using System.IO; using System.Linq; using System.Security.Cryptography; using System.Windows.Forms;namespace ImageDuplicate {public partial clas…...

浅谈冯诺依曼体系和操作系统
🌎冯诺依曼体系结构 文章目录 冯诺依曼体系结构 认识冯诺依曼体系结构 硬件分类 各个硬件的简单认识 输入输出设备 中央处理器 存储器 关于内存 对冯诺依曼体系的理解 操作系统 操作系统…...

Good Bye 2023
Good Bye 2023 Good Bye 2023 A. 2023 题意:序列a中所有数的乘积应为2023,现在给出序列中的n个数,找到剩下的k个数并输出,报告不可能。 思路:把所有已知的数字乘起来,判断是否整除2023,不够…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...
