【数值分析】LU分解解Ax=b,matlab自己编程实现
LU分解(直接三角分解,Doolittle分解)
A x = b , A = L U Ax=b \,\,,\,\, A=LU Ax=b,A=LU
{ L y = b U x = y \begin{cases} Ly=b \\ Ux=y \end{cases} {Ly=bUx=y
矩阵 L {L} L 的对角元素为 1 {1} 1 ,矩阵 U {U} U 的第一行和 A {A} A 相同。
步骤:
1. 矩阵 L 的对角元素为 1 ,矩阵 U 的第一行和 A 相同。 2. 迭代 , j = 1 , 2 , ⋯ n − 1 算 L 的第 j 列 , L i , j = A i , j − ∑ r = 1 j − 1 L i , r U r , j U j , j , i = j + 1 , j + 2 , ⋯ , n 算 U 的第 j + 1 行 , U j + 1 , k = A j + 1 , k − ∑ r = 1 j L j + 1 , r U r , k L j + 1 , j + 1 , k = j + 1 , j + 2 , ⋯ , n 3. 回代 , y i = b i − ∑ j = 1 i − 1 L i , j y j , i = 1 , 2 , ⋯ , n x i = y i − ∑ j = i + 1 n x j ⋅ U i , j U i , i , i = n , n − 1 , ⋯ , 1 \begin{align*} 1.& 矩阵 L 的对角元素为 1 ,矩阵U 的第一行和A相同。 \\ \\ 2. & 迭代 \,\,,\,\, j=1,2, \cdots n-1 \\ \\ &算L的第j列 \,\,,\,\, L_{i,j}= \frac{A_{i,j}- \sum_{r=1}^{j-1}L_{i,r}U_{r,j}}{U_{j,j}},i=j+1,j+2,\cdots ,n \\ \\ &算U的第j+1行 \,\,,\,\, U_{j+1,k}= \frac{A_{j+1,k}- \sum_{r=1}^{ j}L_{j+1,r}U_{r,k}}{L_{j+1,j+1}} ,k=j+1,j+2,\cdots ,n \\ \\ 3.& 回代 \,\,,\,\, \\ \\ & y_i= b_i- \sum_{j=1}^{ i-1}L_{i,j}y_j,i=1,2,\cdots ,n \\ \\ &x_i= \frac{y_i- \sum_{j=i+1}^{ n}x_j \cdot U_{i,j}}{U_{i,i}} \,\,,\,\, i=n,n-1, \cdots ,1 \end{align*} 1.2.3.矩阵L的对角元素为1,矩阵U的第一行和A相同。迭代,j=1,2,⋯n−1算L的第j列,Li,j=Uj,jAi,j−∑r=1j−1Li,rUr,j,i=j+1,j+2,⋯,n算U的第j+1行,Uj+1,k=Lj+1,j+1Aj+1,k−∑r=1jLj+1,rUr,k,k=j+1,j+2,⋯,n回代,yi=bi−j=1∑i−1Li,jyj,i=1,2,⋯,nxi=Ui,iyi−∑j=i+1nxj⋅Ui,j,i=n,n−1,⋯,1
matlab实现
%% Ax=b例子
A = [16 -12 2 4;12 -8 6 10;3 -13 9 23;-6 14 1 -28];
b = [17 36 -49 -54]';
[x,L,U] = LUsolve(A,b)%% LU分解解Ax=b
% 输入方阵A,向量b
% 输出解x,L、U矩阵
function [x,L,U] = LUsolve(A,b)n = size(A);L = eye(n);U(1,[1:n]) = A(1,[1:end]);for j = 1:n-1 % 对U是行号,对L是列号for i = j+1:n % 算L第i行j列L(i,j) = A(i,j);for r = 1:j-1L(i,j) = L(i,j)- L(i,r)*U(r,j);endL(i,j) = L(i,j)/U(j,j);endfor k = j+1:n % 算U第j+1行k列U(j+1,k) = A(j+1,k);for r = 1:jU(j+1,k) = U(j+1,k)-L(j+1,r)*U(r,k);endU(j+1,k) = U(j+1,k)/L(j+1,j+1);endend% 回代for i = 1:ny(i) = b(i);for j = 1:i-1y(i) = y(i)-L(i,j)*y(j);endendfor i=n:-1:1 x(i) = y(i);for j=n:-1:i+1x(i) = x(i)-U(i,j)*x(j);endx(i) = x(i)/U(i,i);endx = x';
end
相关文章:

【数值分析】LU分解解Ax=b,matlab自己编程实现
LU分解(直接三角分解,Doolittle分解) A x b , A L U Axb \,\,,\,\, ALU Axb,ALU { L y b U x y \begin{cases} Lyb \\ Uxy \end{cases} {LybUxy 矩阵 L {L} L 的对角元素为 1 {1} 1 ,矩阵 U {U} U 的第一行和 A {A} A …...

华为HCIE-Datacom课程介绍
厦门微思网络HCIE-Datacom课程介绍 一、认证简介 HCIE-Datacom(Huawei Certified ICT Expert-Datacom)认证是华为认证体系中的顶级认证,HCIE-Datacom认证定位具备坚实的企业网络跨场景融合解决方案理论知识,能够使用华为数通产品…...
-QTableWight添加行和删除空行)
QT(C++)-QTableWight添加行和删除空行
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 1、前言2、QTableWidget的添加行3、删除行 1、前言 最近要用QT开发项目,对QT不是很熟,就根据网上的查到的知识和自己的摸索,将一…...

软件测试/测试开发丨Python 面向对象编程思想
面向对象是什么 Python 是一门面向对象的语言面向对象编程(OOP):Object Oriented Programming 所谓的面向对象,就是在编程的时候尽可能的去模拟真实的现实世界,按照现实世界中的逻辑去处理问题,分析问题中…...

一次降低进程IO延迟的性能优化实践——基于block层bfq调度器
如果有个进程正频繁的读写文件,此时你vim查看一个新文件,将会出现明显卡顿。即便你vim查看的文件只有几十M,也可能会出现卡顿。相对的,线上经常遇到IO敏感进程偶发IO超时问题。这些进程一次读写的文件数据量很少,正常几…...

C语言易错知识点十(指针(the final))
❀❀❀ 文章由不准备秃的大伟原创 ❀❀❀ ♪♪♪ 若有转载,请联系博主哦~ ♪♪♪ ❤❤❤ 致力学好编程的宝藏博主,代码兴国!❤❤❤ 许久不见,甚是想念,真的是时间时间,你慢些吧,不能再让头发变秃…...

React 18 新增的钩子函数
React 18 引入了一些新的钩子函数,用于处理一些常见的场景和问题。以下是 React 18 中引入的一些新钩子函数以及它们的代码示例和使用场景: useTransition: 代码示例:import { useTransition } from react;function MyComponent()…...
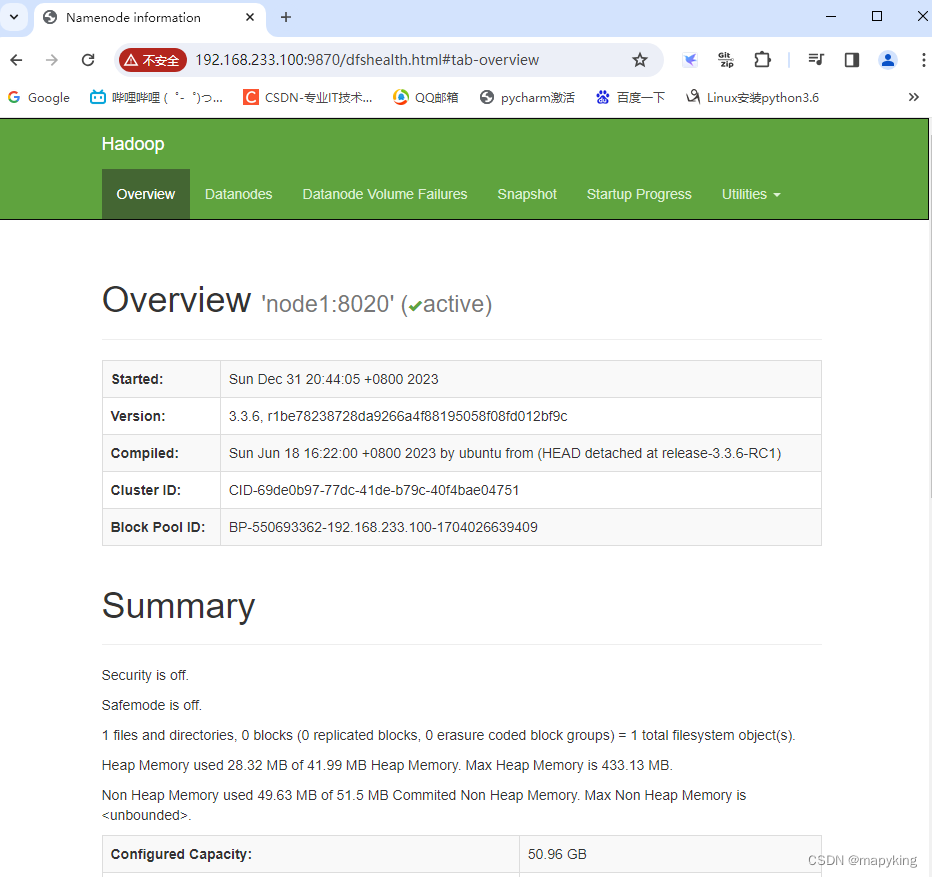
安装与部署Hadoop
一、前置安装准备1、机器2、java3、创建hadoop用户 二、安装Hadoop三、环境配置1、workers2、hadoop-env.sh3、core-site.xml4、hdfs-site.xml5、linux中Hadoop环境变量 四、启动hadoop五、验证 一、前置安装准备 1、机器 主机名ip服务node1192.168.233.100NameNode、DataNod…...
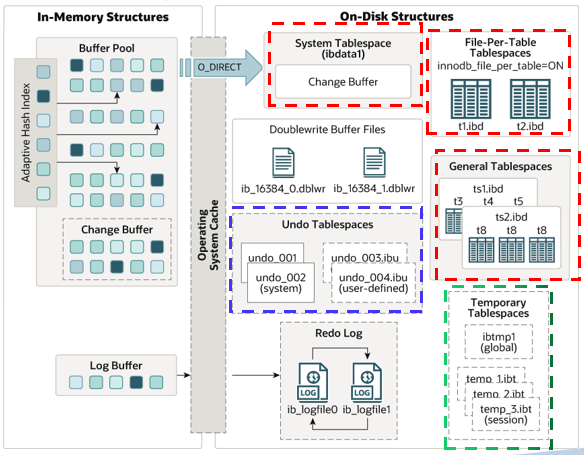
MySQL 8.0 InnoDB Tablespaces之General Tablespaces(通用表空间/一般表空间)
文章目录 MySQL 8.0 InnoDB Tablespaces之General Tablespaces(通用表空间/一般表空间)General tablespaces(通用表空间/一般表空间)通用表空间的功能通用表空间的限制 创建通用表空间(一般表空间)创建语法…...

循环生成对抗网络(CycleGAN)
一、说明 循环生成对抗网络(CycleGAN)是一种训练深度卷积神经网络以执行图像到图像翻译任务的方法。网络使用不成对的数据集学习输入和输出图像之间的映射。 二、基本介绍 CycleGAN 是图像到图像的翻译模型,就像Pix2Pix一样。Pix2Pix模型面临…...

数组--53.最大子数组和/medium
53.最大子数组和 1、题目2、题目分析3、解题步骤4、复杂度最优解代码示例5、抽象与扩展 1、题目 给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。 子数组 是数组中的一个连…...

centos 编译安装 python 和 openssl
安装环境: centos 7.9 : python 3.10.5 和 openssl 3.0.12 centos 6.10 : python 3.10.5 和 openssl 1.1.1 两个环境都能安装成功,可以正常使用。 安装 openssl 下载地址 下载后解压,进入到解压目录 执行…...
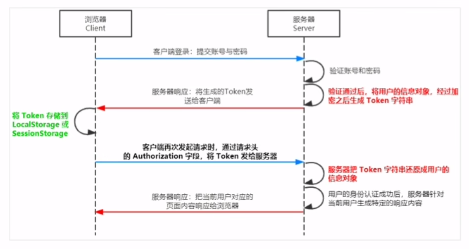
【nodejs】前后端身份认证
前后端身份认证 一、web开发模式 服务器渲染,前后端分离。 不同开发模式下的身份认证: 服务端渲染推荐使用Session认证机制前后端分离推荐使用JWT认证机制 二、session认证机制 1.HTTP协议的无状态性 了解HTTP协议的无状态性是进一步学习Session认…...

数据结构【线性表篇】(三)
数据结构【线性表篇】(三) 文章目录 数据结构【线性表篇】(三)前言为什么突然想学算法了?为什么选择码蹄集作为刷题软件? 目录一、双链表二、循环链表三、静态链表 结语 前言 为什么突然想学算法了? > 用较为“官方…...
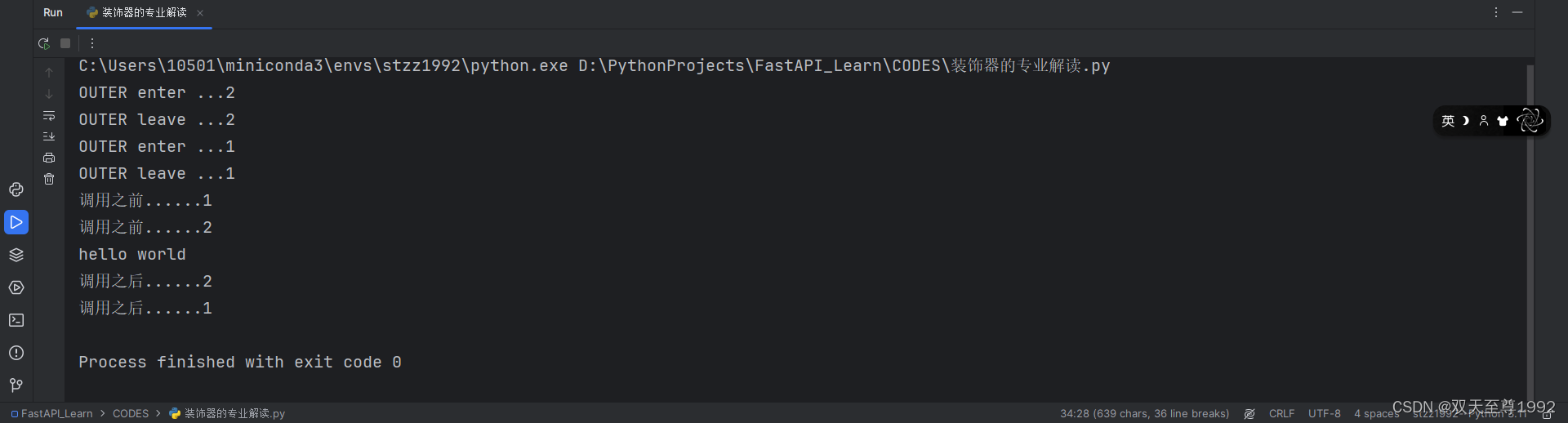
Python装饰器的专业解释
装饰器,其实是用到了闭包的原理来进行操作的。 单个装饰器: 以下是一个简单的例子: def outer(func):print("OUTER enter ...")def wrapper(*args, **kwargs):print("调用之前......")result func(*args, **kwargs)p…...
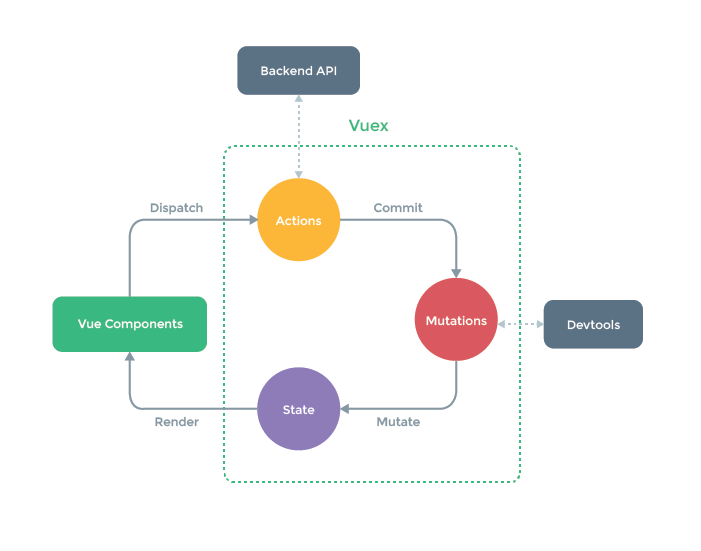
vue3框架笔记
Vue Vue 是一个渐进式的前端开发框架,很容易上手。Vue 目前的版本是 3.x,但是公司中也有很多使用的是 Vue2。Vue3 的 API 可以向下兼容 2,Vue3 中新增了很多新的写法。我们课程主要以 Vue3 为主 官网 我们学习 Vue 需要转变思想࿰…...
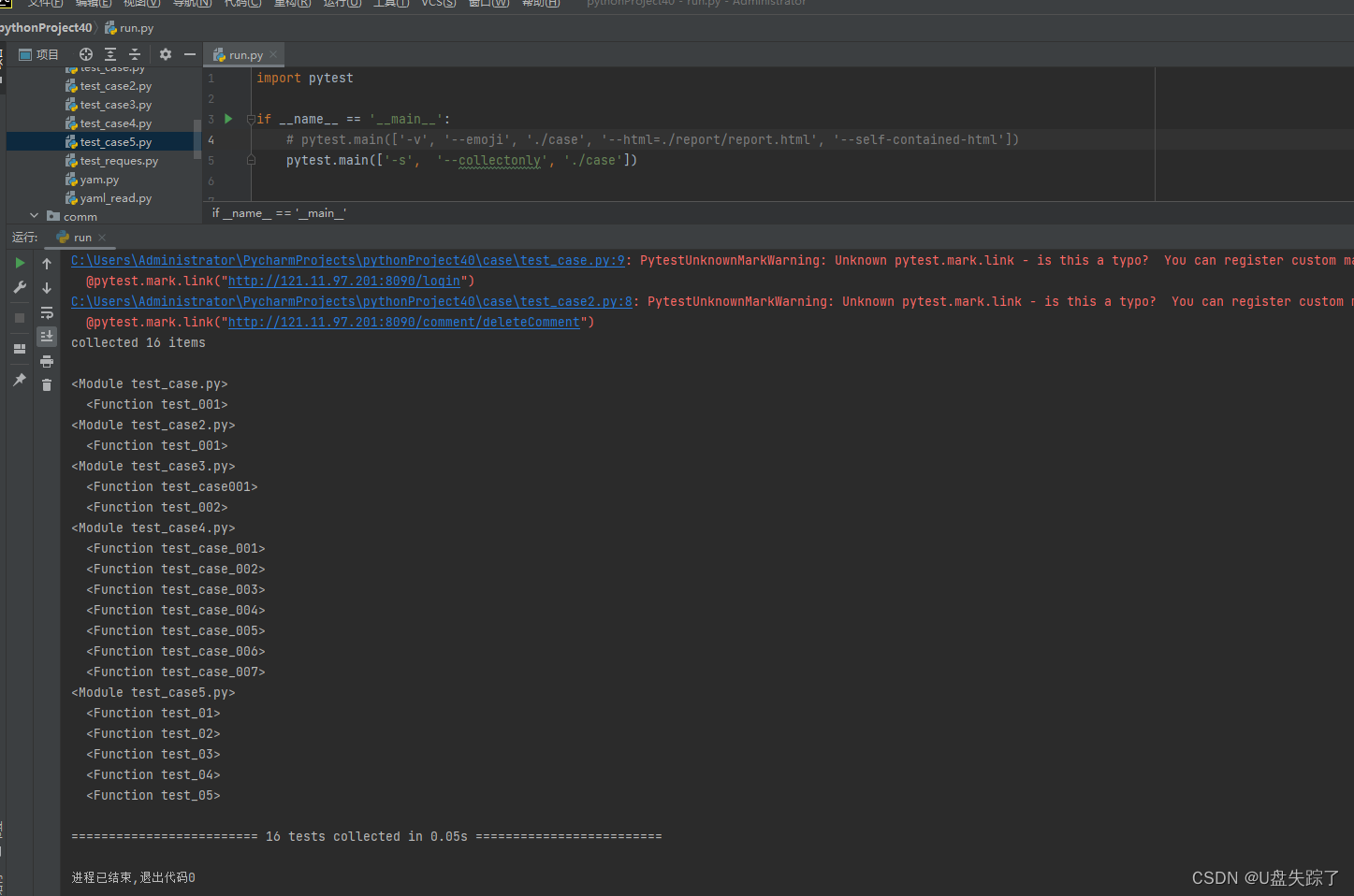
pytest --collectonly 收集测试案例
pytest --collectonly 是一条命令行指令,用于在运行 pytest 测试时仅收集测试项而不执行它们。它会显示出所有可用的测试项列表,包括测试模块、测试类和测试函数,但不会执行任何实际的测试代码。 这个命令对于查看项目中的测试结构和确保所有…...
dev express 15.2图表绘制性能问题(dotnet绘图表)
dev express 15.2 绘制曲线 前端代码 <dxc:ChartControl Grid.Row"1"><dxc:XYDiagram2D EnableAxisXNavigation"True"><dxc:LineSeries2D x:Name"series" CrosshairLabelPattern"{}{A} : {V:F2}"/></dxc:XYDi…...

WorkPlus:领先的IM即时通讯软件,打造高效沟通协作新时代
在当今快节奏的商业环境中,高效沟通和协作是企业成功的关键。而IM即时通讯软件作为实现高效沟通的利器,成为了现代企业不可或缺的一部分。作为一款领先的IM即时通讯软件,WorkPlus以其卓越的性能和独特的功能,助力企业打造高效沟通…...
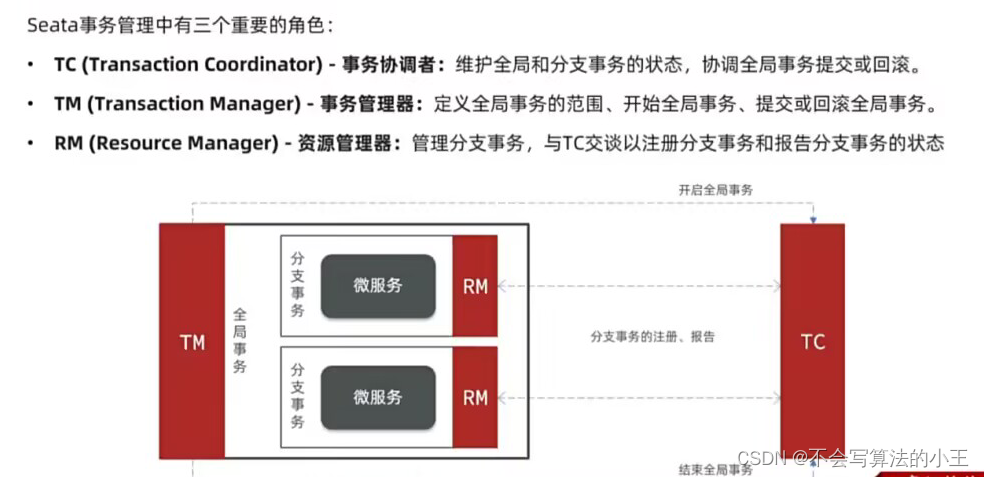
学习SpringCloud微服务
SpringCloud 微服务单体框架微服务框架SpringCloud微服务拆分微服务差分原则拆分商品服务拆分购物车服务拆分用户服务拆分交易服务拆分支付服务服务调用RestTemplate远程调用 微服务拆分总结 服务治理注册中心Nacos注册中心服务注册服务发现 OpenFeign实现远程调用快速入门引入…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...
