C++每日一练(8):图像相似度
题目描述
给出两幅相同大小的黑白图像(用0-1矩阵)表示,求它们的相似度。
说明:若两幅图像在相同位置上的像素点颜色相同,则称它们在该位置具有相同的像素点。两幅图像的相似度定义为相同像素点数占总像素点数的百分比。
输入
第一行包含两个整数m和n,表示图像的行数和列数,中间用单个空格隔开。1 <= m <= 100, 1 <= n <= 100。 之后m行,每行n个整数0或1,表示第一幅黑白图像上各像素点的颜色。相邻两个数之间用单个空格隔开。 之后m行,每行n个整数0或1,表示第二幅黑白图像上各像素点的颜色。相邻两个数之间用单个空格隔开。
输出
一个实数,表示相似度(以百分比的形式给出),精确到小数点后两位(带百分号)。
输入样例
3 3
1 0 1
0 0 1
1 1 0
1 1 0
0 0 1
0 0 1
输出样例
44.44%
参考答案
#include<bits/stdc++.h>
using namespace std;
int a[101][101],b[101][101],s,x;
int main(){int n,m;cin >> n >> m;for(int i = 1;i <= n;i ++){for(int j = 1;j <= m;j ++){cin >> a[i][j];}}for(int i = 1;i <= n;i ++){for(int j = 1;j <= m;j ++){cin >> b[i][j];}}x = n * m;for(int i = 1;i <= n;i ++){for(int j = 1;j <= m;j ++){if(a[i][j] == b[i][j]) s ++;}}printf("%.2f",s*100.00/x);cout << "%";
} 相关文章:

C++每日一练(8):图像相似度
题目描述 给出两幅相同大小的黑白图像(用0-1矩阵)表示,求它们的相似度。 说明:若两幅图像在相同位置上的像素点颜色相同,则称它们在该位置具有相同的像素点。两幅图像的相似度定义为相同像素点数占总像素点数的百分比。…...
C++面试宝典第12题:数组元素相除
题目 从控制台输入若干个整数作为数组,将数组中每一个元素除以第一个元素的结果,作为新的数组元素值。比如:可以先输入3,作为数组元素的个数;然后输入3个整数,作为数组元素的值。 解析 这道题本身并不复杂,但里面隐藏了不少“坑点”和“雷区”,主要考察应聘者全面思考问…...

oCPC实践录 | 目标ROI的出价与转化回传调控算法
这篇文章我们聊聊广告主在oCPC下,怎么调控自己的出价或者回传转化优化自己的ROI。 ROI是广告主最关心的指标了,根据oCPC出价的基本原理ocpc_bid pcvr * given_cpa * k, 广告主在整个出价中有两个可以控制的变量来影响出价,一个是直接的give…...

百倍量化之Dbcd-v2中性策略
Dbcd-v2中性策略 1. 指标含义 该指标主要是计算偏置的因子,并根据偏置的平均来分析这个股票的稳定性。相比于v1,策略是更换了dbcd的计算方式 第一步主要操作就是计算当前值和前段时间的平均值的偏置 ma = bt.indicators.SimpleMovingAverage(self.data, period=self.p.peri…...

系统学习Python——装饰器:函数装饰器-[装饰器状态保持方案:函数属性]
分类目录:《系统学习Python》总目录 如果我们没有在使用Python3.X并因此无法利用一条nonlocal语句,或者我们希望代码具有可移植性,能在Python3.X和Python2.X上同时工作一一我们仍然能够针对某些可改变的状态使用函数属性来避免使用全局变量和…...
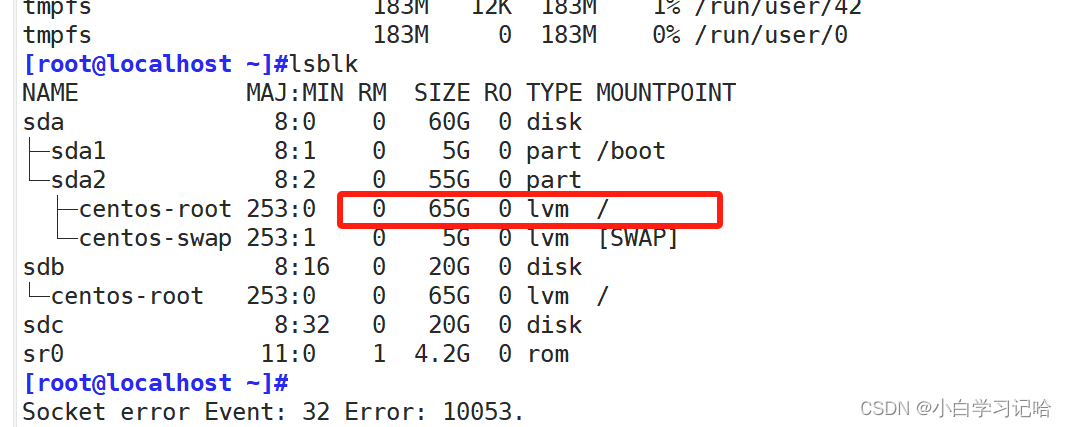
逻辑卷学习后续----------缩容
一、缩容:缩减大小 ext4可以 , xfs无法缩减,缩减会影响业务 1.解挂载 2.检查文件系统完整性 3.缩减文件系统 4.缩减逻辑卷上下一致 5.再挂载回去 添加磁盘 文件系统只能装ext4 缩减文件系统 resize2fs 挂载失败需要重新安装文件系统…...
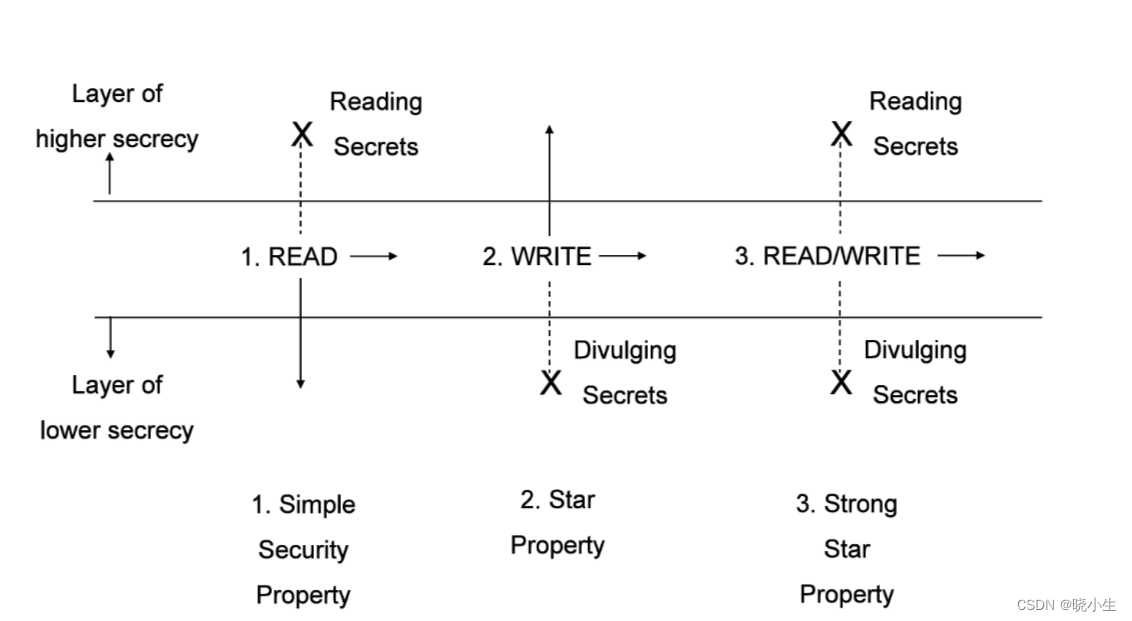
15-网络安全框架及模型-BLP机密性模型
目录 BLP机密性模型 1 背景概述 2 模型原理 3 主要特性 4 优势和局限性 5 困难和挑战 6 应用场景 7 应用案例 BLP机密性模型 1 背景概述 BLP模型,全称为Bell-LaPadula模型,是在1973年由D.Bell和J.LaPadula在《Mathematical foundations and mod…...
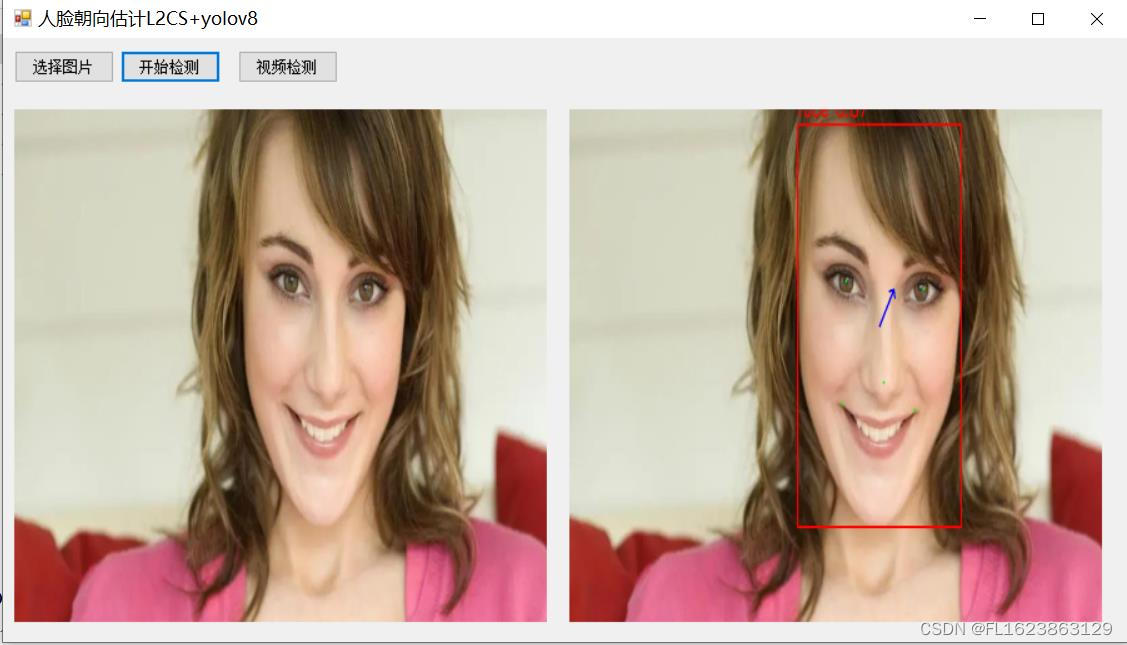
[C#]OpenCvSharp结合yolov8-face实现L2CS-Net眼睛注视方向估计或者人脸朝向估计
源码地址: github地址:https://github.com/Ahmednull/L2CS-Net L2CS-Net介绍: 眼睛注视(eye gaze) 是在各种应用中使用的基本线索之一。 它表示用户在人机交互和开放对话系统中的参与程度。此外,它还被用…...

[2024区块链开发入门指引] - 比特币与区块链诞生
一份为小白用户准备的免费区块链基础教程 工欲善其事,必先利其器 Web3开发中,各种工具、教程、社区、语言框架.。。。 种类繁多,是否有一个包罗万象的工具专注与Web3开发和相关资讯能毕其功于一役? 参见另一篇博文👉 2024最全面…...
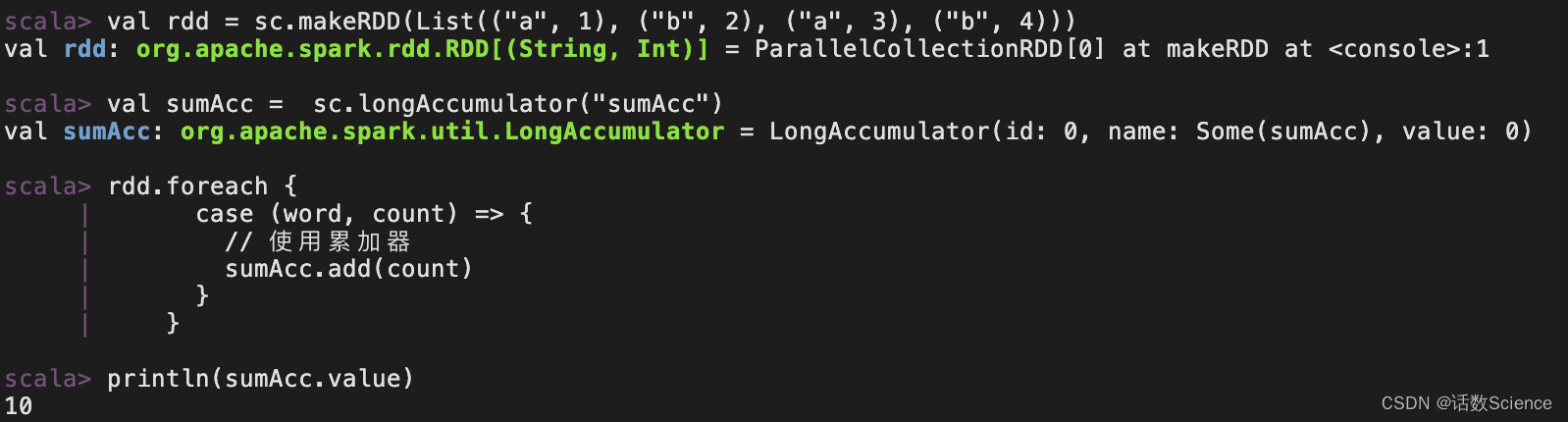
【大数据面试知识点】Spark中的累加器
Spark累加器 累加器用来把Executor端变量信息聚合到Driver端,在driver程序中定义的变量,在Executor端的每个task都会得到这个变量的一份新的副本,每个task更新这些副本的值后,传回driver端进行merge。 累加器一般是放在行动算子…...

深度学习核心技术与实践之深度学习基础篇
非书中全部内容,只是写了些自认为有收获的部分 神经网络 生物神经元的特点 (1)人体各种神经元本身的构成很相似 (2)早期的大脑损伤,其功能可能是以其他部位的神经元来代替实现的 (3&#x…...

Kafka安装及简单使用介绍
🍓 简介:java系列技术分享(👉持续更新中…🔥) 🍓 初衷:一起学习、一起进步、坚持不懈 🍓 如果文章内容有误与您的想法不一致,欢迎大家在评论区指正🙏 🍓 希望这篇文章对你有所帮助,欢…...
20231229在Firefly的AIO-3399J开发板的Android11使用挖掘机的DTS配置单前后摄像头ov13850
20231229在Firefly的AIO-3399J开发板的Android11使用挖掘机的DTS配置单前后摄像头ov13850 2023/12/29 11:10 开发板:Firefly的AIO-3399J【RK3399】 SDK:rk3399-android-11-r20211216.tar.xz【Android11】 Android11.0.tar.bz2.aa【ToyBrick】 Android11.…...

九台虚拟机网站流量分析项目启动步骤
文章目录 零、操作概述一、服务器分配二、9台虚拟机相互免密登录三、Nginx(反向代理服务器)四、Tomcat(Web服务器)五、测试Nginx反向代理是否成功六、Flume集群配置七、修改LogDemo项目八、项目1703FluxStorm九、Hadoop集群十、整个集群的启动十一、部署项目十二、测试项目…...

迅软科技助力高科技防泄密:从华为事件中汲取经验教训
近期,涉及华为芯片技术被窃一事引起广泛关注。据报道,华为海思的两个高管张某、刘某离职后成立尊湃通讯,然后以支付高薪、股权支付等方式,诱导多名海思研发人员跳槽其公司,并指使这些人员在离职前通过摘抄、截屏等方式…...
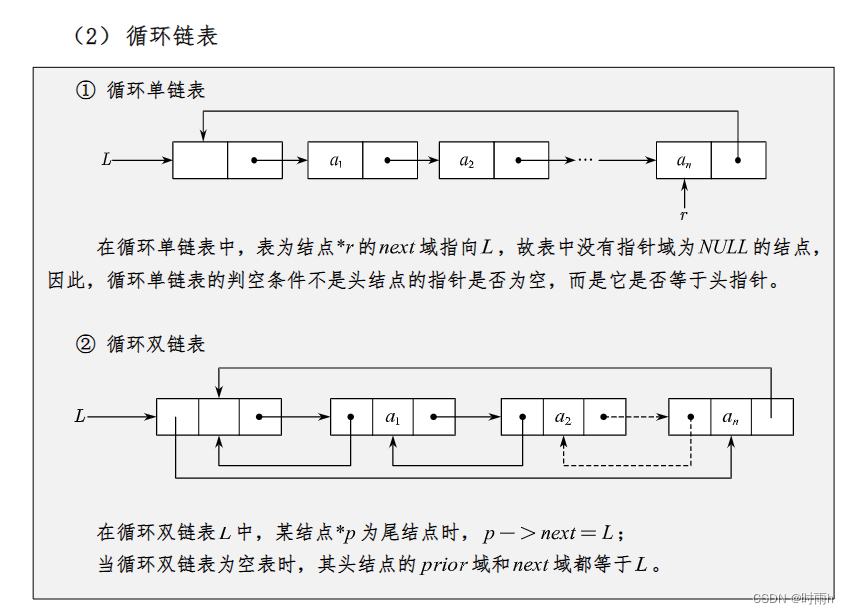
数据结构期末复习(2)链表
链表 链表(Linked List)是一种常见的数据结构,用于存储一系列具有相同类型的元素。链表由节点(Node)组成,每个节点包含两部分:数据域(存储元素值)和指针域(指…...
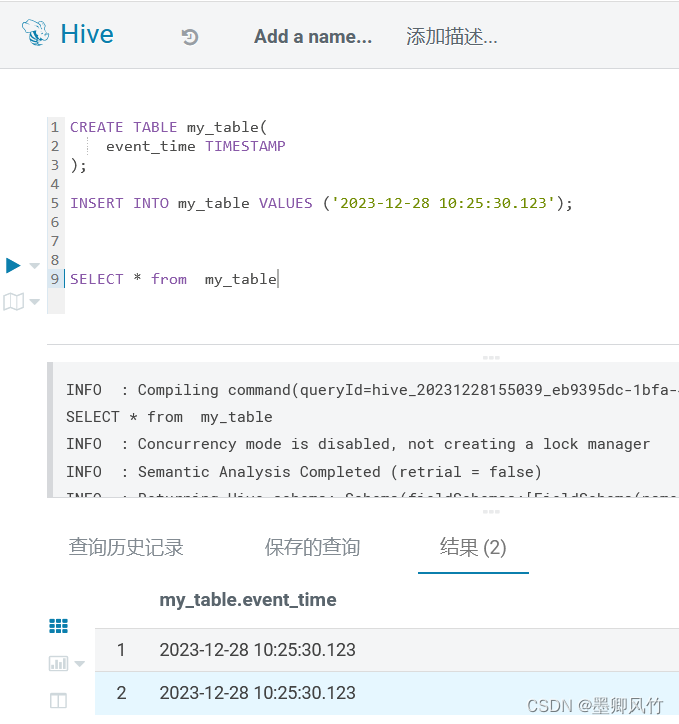
Hive中支持毫秒级别的时间精度
实际上,Hive 在较新的版本中已经支持毫秒级别的时间精度。你可以通过设置 hive.exec.default.serialization.format 和 mapred.output.value.format 属性为 1,启用 Hive 的时间精度为毫秒级。可以使用以下命令进行设置: set hive.exec.defau…...
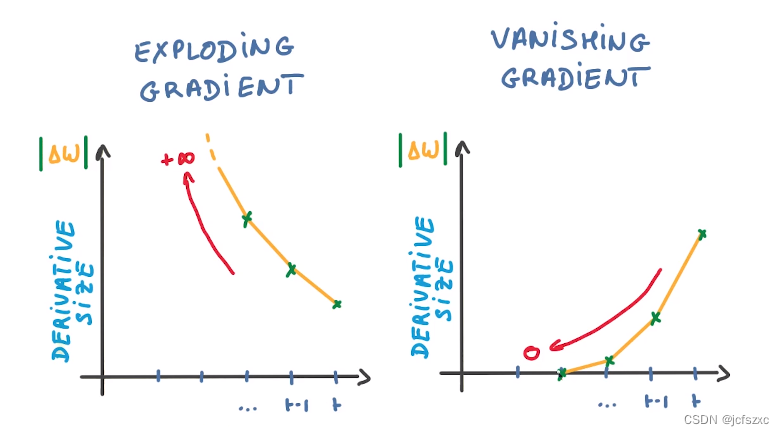
【深度学习:Recurrent Neural Networks】循环神经网络(RNN)的简要概述
【深度学习】循环神经网络(RNN):连接过去与未来的桥梁 循环神经网络简介什么是循环神经网络 (RNN)?传统 RNN 的架构循环神经网络如何工作?常用激活函数RNN的优点和缺点RNN 的优点:RNN 的缺点: 循…...

HTML 基础
文章目录 01-标签语法标签结构 03-HTML骨架04-标签的关系05-注释06-标题标签07-段落标签08-换行和水平线09-文本格式化标签10-图像标签图像属性 11-路径相对路径绝对路径 12-超链接标签13-音频14-视频 01-标签语法 HTML 超文本标记语言——HyperText Markup Language。 超文本…...

大学物理II-作业1【题解】
1.【单选题】——考查高斯定理 下面关于高斯定理描述正确的是(D )。 A.高斯面上的电场强度是由高斯面内的电荷激发的 B.高斯面上的各点电场强度为零时,高斯面内一定没有电荷 C.通过高斯面的电通量为零时,高斯面上各点电场强度…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...
