当前位置： 首页 > news >正文

线性代数笔记3 1.1

news 2026/2/8 15:50:39

学习视频：

2.2 矩阵运算（二）_哔哩哔哩_bilibili

包括内容：

p10矩阵运算（二）

p11特殊矩阵

p12逆矩阵（一） 

p13逆矩阵（二） 

相关文章：

线性代数笔记3 1.1

学习视频： 2.2 矩阵运算（二）_哔哩哔哩_bilibili 包括内容： p10矩阵运算（二） p11特殊矩阵 p12逆矩阵（一） p13逆矩阵（二）...

编程日记 2024/1/3 6:01:55

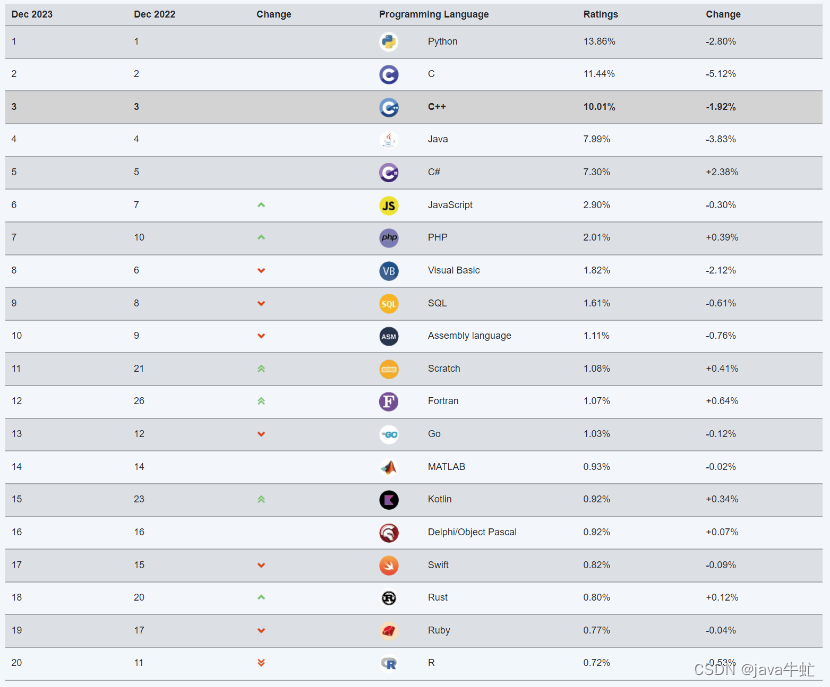
2023年12月编程语言排行榜

TIOBE Index for December 2023 December Headline: C# on its way to become programming language of the year 2023 2023年12月的TIOBE指数：12月头条:c#将成为2023年最佳编程语言 Yes, I know, we have been here before. At the end of 2022, it looked like …...

编程日记 2024/1/3 6:00:54

Redis VS Memcached：选择哪个更适合您的应用？

目录 1、前言 2、概念简介 2.1 Redis 2.2 Memcached 3、数据模型 4、持久性 5、分布式能力 6、性能和扩展性 7、如何选择适合您引用的缓存系统 8、结语 1、前言 Redis和Memcached都是常见的内存缓存系统，用于提升应用程序的性能和可扩展性。它们都具有高…...

编程日记 2024/1/3 5:59:53

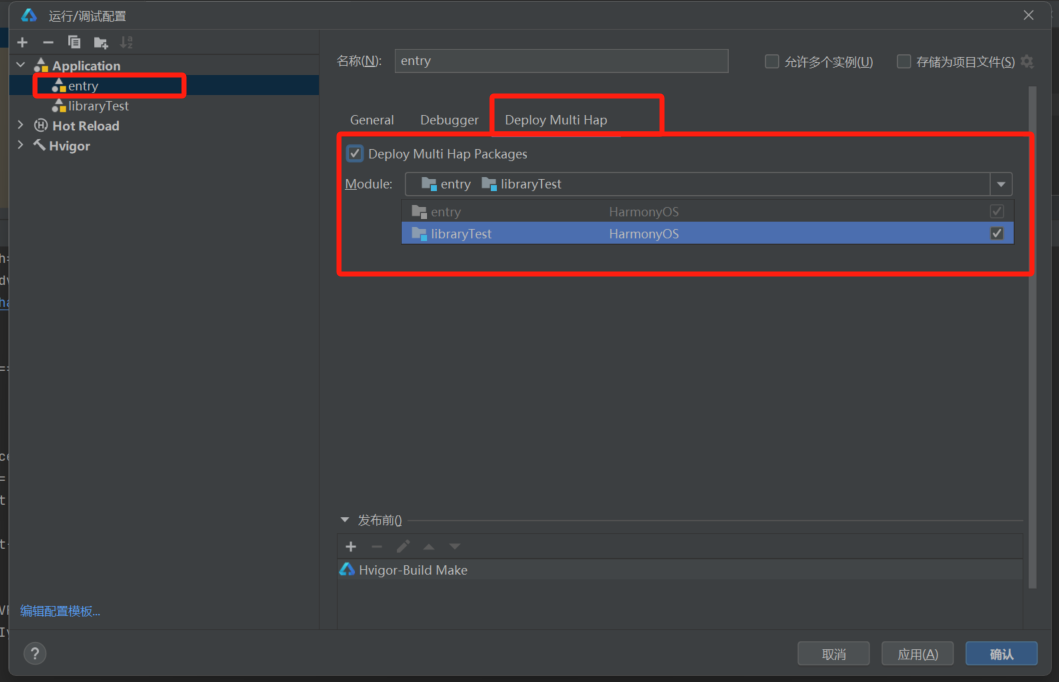
【HarmonyOS开发】共享包HAR和HSP的创建和使用以及三方库的发布

OpenHarmony提供了两种共享包，HAR（Harmony Archive）静态共享包，和HSP（Harmony Shared Package）动态共享包。 HAR与HSP都是为了实现代码和资源的共享，都可以包含代码、C库、资源和配置文件&…...

编程日记 2024/1/3 5:57:52

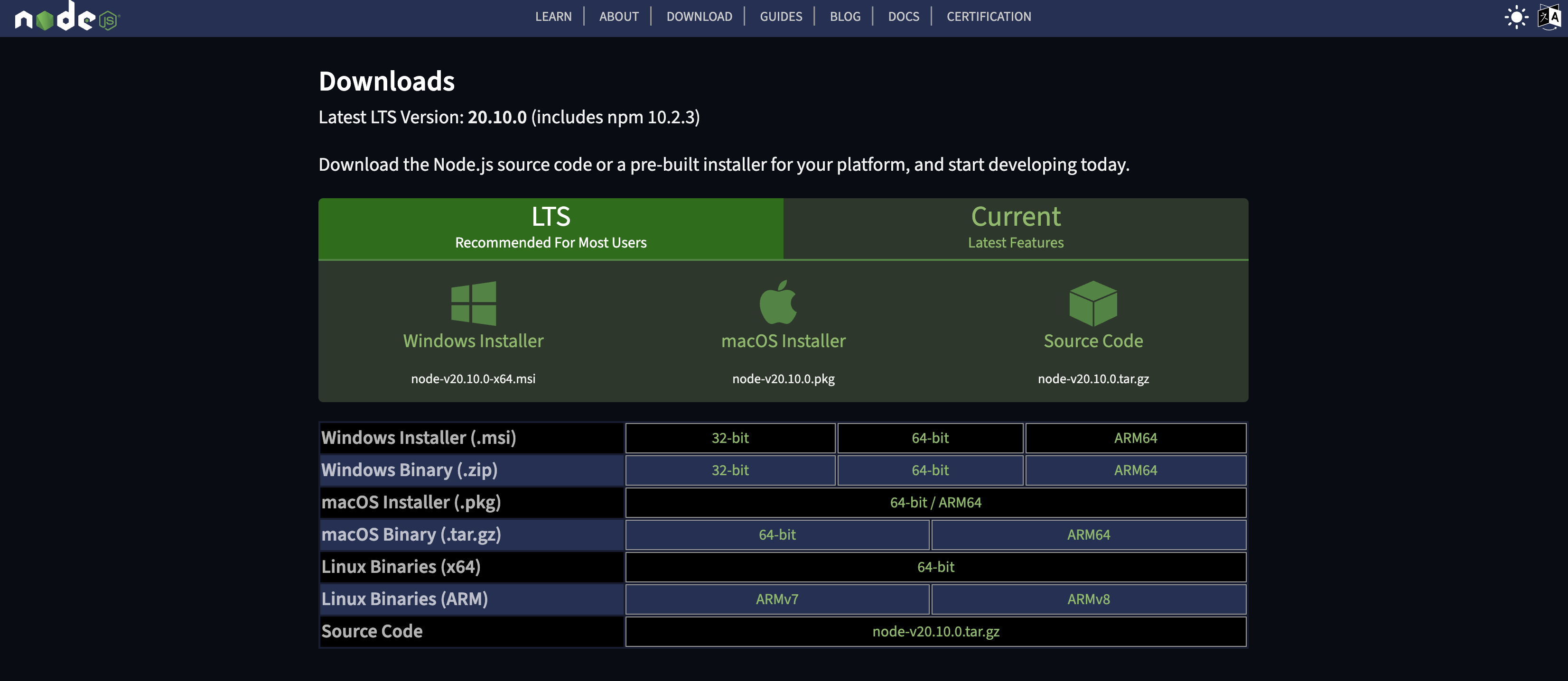
安装 Node.js、npm

安装 nodejs 安装Node.js的最简单的方法是通过软件包管理器。 Node.js官网：https://nodejs.org/en/download/ cd /usr/local/src/wget -c https://nodejs.org/dist/v18.16.0/node-v18.16.0-linux-x64.tar.xz xz -d node-v18.16.0-linux-x64.tar.xz tar -xf node…...

编程日记 2024/1/3 5:56:50

解决报错：找不到显卡

今天做实验碰到一个问题：torch找不到显卡： 打开任务管理器，独显直接没了，一度以为是要去修电脑了，突然想到上次做实验爆显存，屏蔽了gpu用cpu训练： import os os.environ["CUDA_DEVICE_OR…...

编程日记 2024/1/3 5:55:49

如何使用Node.js快速创建本地HTTP服务器并实现公网访问服务端

💝💝💝欢迎来到我的博客，很高兴能够在这里和您见面！希望您在这里可以感受到一份轻松愉快的氛围，不仅可以获得有趣的内容和知识，也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...

编程日记 2024/1/3 5:53:47

【社交网络分析】课程考试复盘 + 相关资料补充

【社交网络分析】考试后复盘 相关资料补充 写在最前面论述1.描述Logistic回归模型构造损失函数的主要思想。它是如何把线性回归预测模型转化为二分类模型的。Logistic回归模型构造损失函数的主要思想Logistic回归如何将线性回归预测模型转化为二分类模型 2.社交网络分析中面临…...

编程日记 2024/1/3 5:50:44

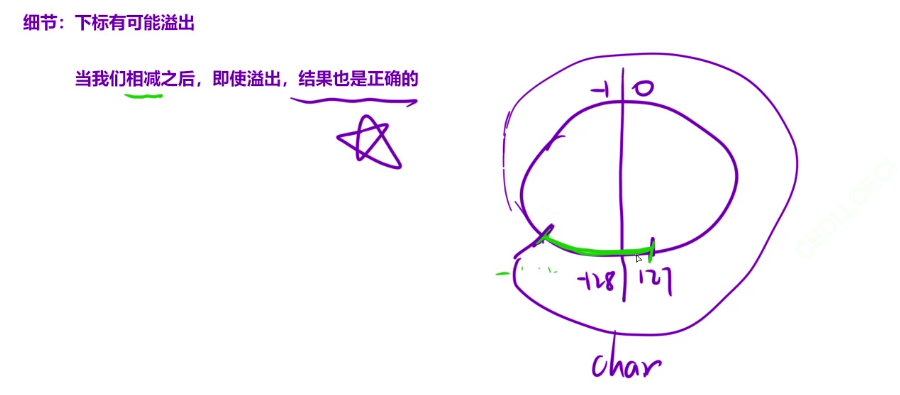
算法——队列+宽搜（BFS）

队列这种数据结构大都服务于一个算法——宽搜（BFS）。宽搜还可以运用到二叉树、图、迷宫最短路径问题、拓扑排序等等 N叉数的层序遍历 N叉树的层序遍历 题目解析 给定一个 N 叉树，返回其节点值的_层序遍历_。（即从左到右&#…...

编程日记 2024/1/3 5:47:40

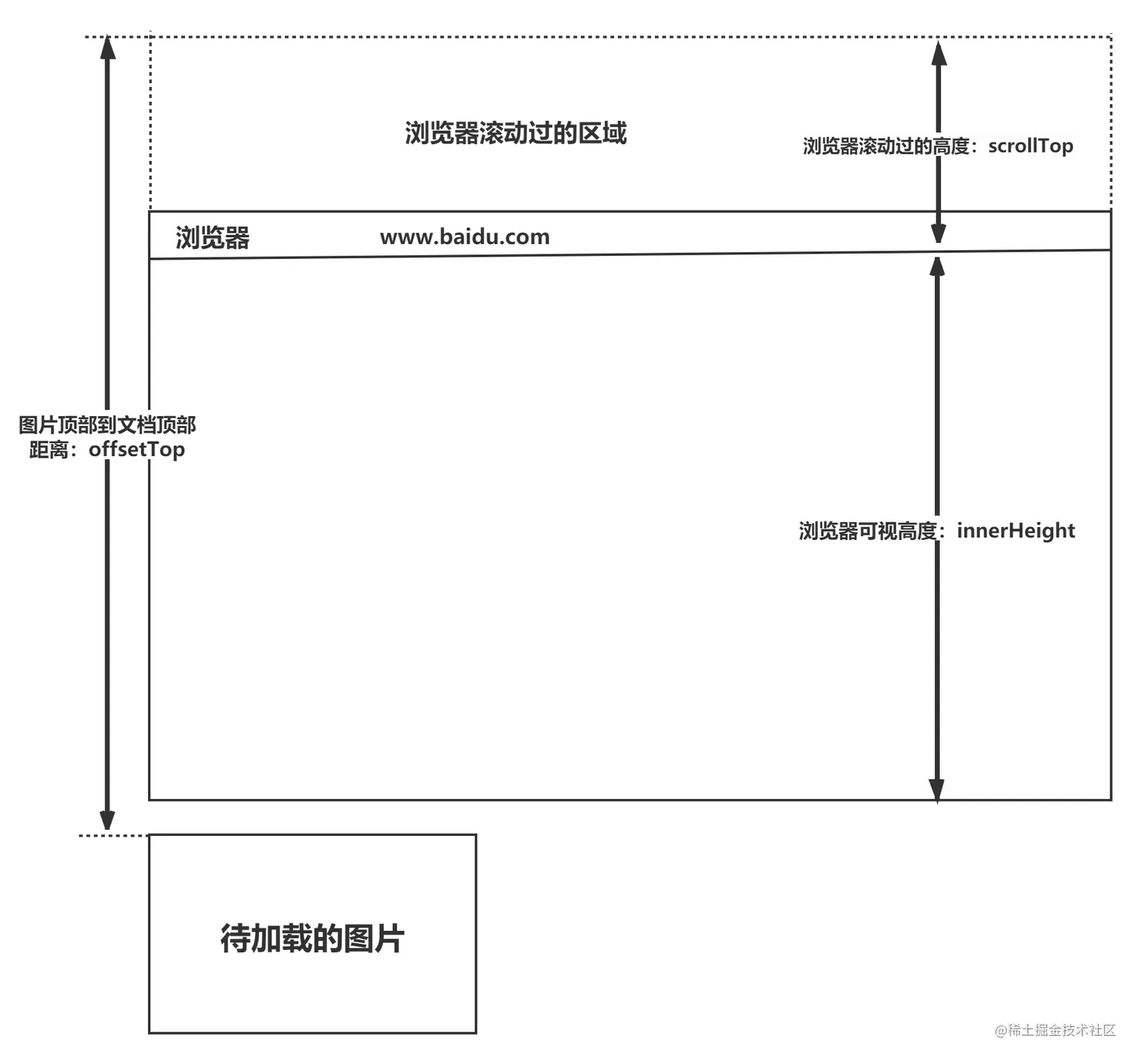
前端八股文（CSS篇）二

目录 1.css中可继承与不可继承属性有哪些 2.link和import的区别 3.transition和animation的区别 4.margin和padding的使用场景 5.：：before和：after的双冒号和单冒号有什么区别？ 6.display:inline-block什么时候会显示间隙 7…...

编程日记 2024/1/3 5:44:36

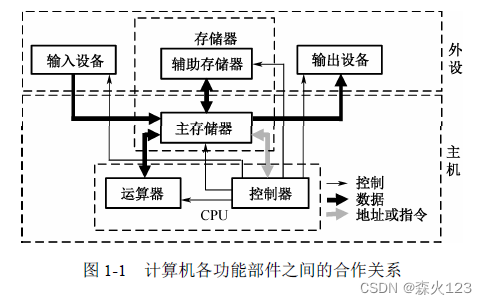
系统架构设计师笔记

第1章计算机组成与体系结构 1.1.1计算机硬件的组成 （1）控制器。控制器是分析和执行指令的部件，也是统一指挥并控制计算机各部件协调工作的中心部件，所依据的是机器指令。控制器的组成包含如下。 ①程序计数器PC：存储下…...

编程日记 2024/1/3 5:42:34

Livox-Mid-360 固态激光雷达ROS格式数据分析

前言： Livox-Mid-360 官方采用livox_ros_driver2ROS功能包发布ROS格式的数据，livox_ros_driver2可以把Livox原始雷达数据转化成ROS格式并以话题的形式发布出去。 下面列举一些雷达的基本概念： 点云帧：雷达驱动每次向外发送的一…...

编程日记 2024/1/3 5:41:33

如何恢复 iPhone 上永久删除的照片？

2007年，苹果公司推出了一款惊天动地的智能手机，也就是后来的iPhone。你会惊讶地发现，迄今为止，苹果公司已经售出了 7 亿部 iPhone 设备。根据最新一项调查数据，智能手机利润的 95% 都进了苹果公司的腰包。 如此受欢迎…...

编程日记 2024/1/3 5:40:32

基于单片机的公交车站自动报站器设计与实现

一、摘要 随着城市交通的快速发展，公交车作为城市公共交通的主要工具，其便捷性和高效性得到了广泛的认可。然而，由于公交车站的广播系统存在一定的局限性，如人工报站容易出现失误、音量大小不一等问题，给乘客带来了不…...

编程日记 2024/1/3 5:39:31

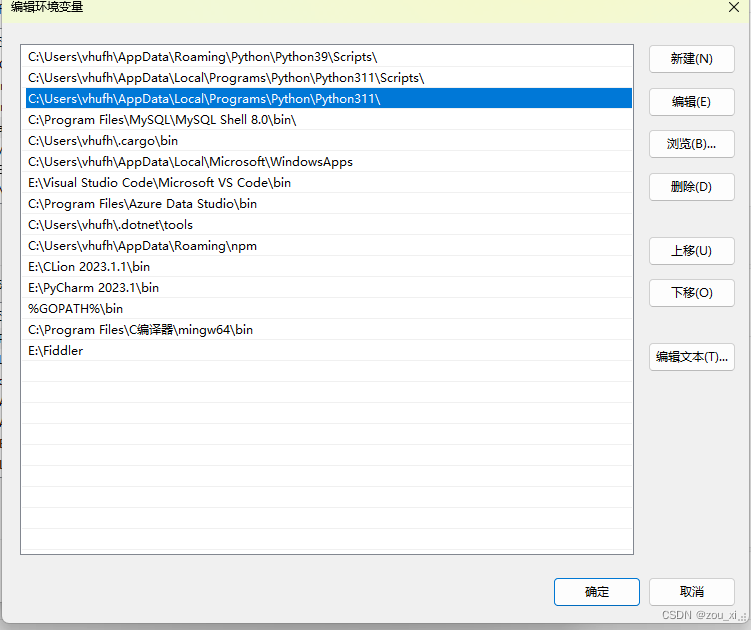
python之Selenium WebDriver安装与使用

首先把python下载安装后，再添加到环境变量中，再打开控制台输入: pip install selenium 正常情况下是安装好的，检查一下“pip show selenium”命令，出现版本号就说明安装好了。 1：如果出现安装错误： 那就用“…...

编程日记 2024/1/3 5:35:28

基于Java+Vue+uniapp微信小程序国产动漫论坛系统设计和实现

博主介绍：✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和学生毕业项目实战,高校老师/讲师/同行交流合作✌ 主要内容：SpringBoot、Vue、SSM、HLM…...

编程日记 2024/1/3 5:34:27

奇因子之和（C语言）

题意： 一个整数的因子，就是所有可以整除这个数的数。奇数指在整数中，不能被 2 整除的数。所谓整数 Z 的奇因子，就是可以整除 Z 的奇数。 给定 N 个正整数，请你求出它们的第二大奇因子的和。当然，如果该数只…...

编程日记 2024/1/3 5:30:23

简单FTP客户端软件开发——VMware安装Linux虚拟机（命令行版）

VMware安装包和Linux系统镜像： 链接：https://pan.baidu.com/s/1UwF4DT8hNXp_cV0NpSfTww?pwdxnoh 提取码：xnoh 这个学期做计网课程设计【简单FTP客户端软件开发】需要在Linux上配置 ftp服务器，故此用VMware安装了Linux虚拟机&…...

编程日记 2024/1/3 5:25:18

ArkTS开发实践

声明式UI基本概念 应用界面是由一个个页面组成，ArkTS是由ArkUI框架提供，用于以声明式开发范式开发界面的语言。 声明式UI构建页面的过程，其实是组合组件的过程，声明式UI的思想，主要体现在两个方面： 描述…...

编程日记 2024/1/3 5:21:15

vue项目中实现预览pdf

vue项目中实现预览pdf 1. iframe <iframe :src"pdfSrc"></iframe> ​data() {return {pdfSrc: http://192.168.0.254:19000/trend/2023/12/27/5635529375174c7798b5fabc22cbec45.pdf,}},​iframe {width: 100%;height: calc(100vh - 132px - 2 * 20px -…...

编程日记 2024/1/3 5:20:14

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析

一、变量声明设计&#xff1a;let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性&#xff0c;这种设计体现了语言的核心哲学。以下是深度解析&#xff1a; 1.1 设计理念剖析 安全优先原则&#xff1a;默认不可变强制开发者明确声明意图 let x 5; …...

编程新知 2025/9/28 20:12:12

Linux应用开发之网络套接字编程(实例篇)

服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

编程新知 2026/2/8 4:37:20

装饰模式（Decorator Pattern）重构java邮件发奖系统实战

前言 现在我们有个如下的需求&#xff0c;设计一个邮件发奖的小系统&#xff0c; 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式&#xff08;Decorator Pattern&#xff09;允许向一个现有的对象添加新的功能&#xff0c;同时又不改变其…...

编程新知 2026/2/8 4:37:00

突破不可导策略的训练难题：零阶优化与强化学习的深度嵌合

强化学习&#xff08;Reinforcement Learning, RL&#xff09;是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程&#xff0c;然后使用强化学习的Actor-Critic机制&#xff08;中文译作“知行互动”机制&#xff09;&#xff0c;逐步迭代求解…...

编程新知 2026/2/5 4:17:42

Golang 面试经典题：map 的 key 可以是什么类型？哪些不可以？

Golang 面试经典题&#xff1a;map 的 key 可以是什么类型&#xff1f;哪些不可以&#xff1f; 在 Golang 的面试中&#xff0c;map 类型的使用是一个常见的考点&#xff0c;其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

编程新知 2025/12/20 7:42:02

模型参数、模型存储精度、参数与显存

模型参数量衡量单位 M&#xff1a;百万&#xff08;Million&#xff09; B&#xff1a;十亿&#xff08;Billion&#xff09; 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的&#xff0c;但是一个参数所表示多少字节不一定&#xff0c;需要看这个参数以什么…...

编程新知 2025/12/20 12:32:08

三维GIS开发cesium智慧地铁教程（5）Cesium相机控制

一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点&#xff1a; 路径验证&#xff1a;确保相对路径.…...

编程新知 2025/12/1 19:23:04

阿里云ACP云计算备考笔记 (5)——弹性伸缩

目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

编程新知 2026/1/22 6:07:24

django filter 统计数量 按属性去重

在Django中&#xff0c;如果你想要根据某个属性对查询集进行去重并统计数量&#xff0c;你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求&#xff1a; 方法1&#xff1a;使用annotate()和Count 假设你有一个模型Item&#xff0c;并且你想…...

编程新知 2026/1/11 2:37:51

五年级数学知识边界总结思考-下册

目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解&#xff1a;由来、作用与意义**一、知识点核心内容****二、知识点的由来&#xff1a;从生活实践到数学抽象****三、知识的作用&#xff1a;解决实际问题的工具****四、学习的意义&#xff1a;培养核心素养…...

编程新知 2025/10/7 4:57:55