leetcode贪心(单调递增的数字、监控二叉树)
738.单调递增的数字
给定一个非负整数 N,找出小于或等于 N 的最大的整数,同时这个整数需要满足其各个位数上的数字是单调递增。
(当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时,我们称这个整数是单调递增的。)
示例 1:
输入: N = 10
输出: 9
示例 2:
输入: N = 1234
输出: 1234
示例 3:
输入: N = 332
输出: 299
说明: N 是在 [0, 10^9] 范围内的一个整数。
class Solution:def monotoneIncreasingDigits(self, N: int) -> int:# 将整数转换为字符串strNum = str(N)# flag用来标记赋值9从哪里开始# 设置为字符串长度,为了防止第二个for循环在flag没有被赋值的情况下执行flag = len(strNum)# 从右往左遍历字符串for i in range(len(strNum) - 1, 0, -1):# 如果当前字符比前一个字符小,说明需要修改前一个字符if strNum[i - 1] > strNum[i]:flag = i # 更新flag的值,记录需要修改的位置# 将前一个字符减1,以保证递增性质strNum = strNum[:i - 1] + str(int(strNum[i - 1]) - 1) + strNum[i:]# 将flag位置及之后的字符都修改为9,以保证最大的递增数字for i in range(flag, len(strNum)):strNum = strNum[:i] + '9' + strNum[i + 1:]# 将最终的字符串转换回整数并返回return int(strNum)
968.监控二叉树
力扣题目链接(opens new window)
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:

输入:[0,0,null,0,0]
输出:1
解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
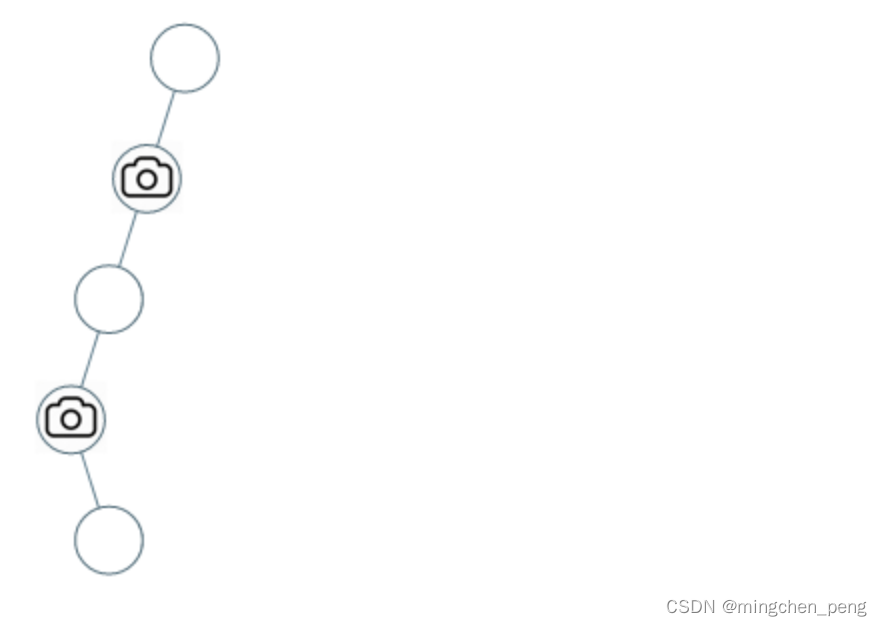
输入:[0,0,null,0,null,0,null,null,0]
输出:2
解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
提示:
给定树的节点数的范围是 [1, 1000]。
每个节点的值都是 0。
class Solution:# Greedy Algo:# 从下往上安装摄像头:跳过leaves这样安装数量最少,局部最优 -> 全局最优# 先给leaves的父节点安装,然后每隔两层节点安装一个摄像头,直到Head# 0: 该节点未覆盖# 1: 该节点有摄像头# 2: 该节点有覆盖def minCameraCover(self, root: TreeNode) -> int:# 定义递归函数result = [0] # 用于记录摄像头的安装数量if self.traversal(root, result) == 0:result[0] += 1return result[0]def traversal(self, cur: TreeNode, result: List[int]) -> int:if not cur:return 2left = self.traversal(cur.left, result)right = self.traversal(cur.right, result)# 情况1: 左右节点都有覆盖if left == 2 and right == 2:return 0# 情况2:# left == 0 && right == 0 左右节点无覆盖# left == 1 && right == 0 左节点有摄像头,右节点无覆盖# left == 0 && right == 1 左节点无覆盖,右节点有摄像头# left == 0 && right == 2 左节点无覆盖,右节点覆盖# left == 2 && right == 0 左节点覆盖,右节点无覆盖if left == 0 or right == 0:result[0] += 1return 1# 情况3:# left == 1 && right == 2 左节点有摄像头,右节点有覆盖# left == 2 && right == 1 左节点有覆盖,右节点有摄像头# left == 1 && right == 1 左右节点都有摄像头if left == 1 or right == 1:return 2相关文章:

leetcode贪心(单调递增的数字、监控二叉树)
738.单调递增的数字 给定一个非负整数 N,找出小于或等于 N 的最大的整数,同时这个整数需要满足其各个位数上的数字是单调递增。 (当且仅当每个相邻位数上的数字 x 和 y 满足 x < y 时,我们称这个整数是单调递增的。ÿ…...

如何在win7同样支持Webview2 在 WPF 中使用本地 Webview2 ,如何不依赖系统 Runtime
项目运行环境: .Net Framework 4.5.2 Windows 7 x64 Service Pack 1 WebView2 Microsoft.WebView2.FixedVersionRuntime.120.0.2210.91.x64 考虑到很多老项目,本项目使用的是.Net Framework 4.5.2,.Net 更高版本的其实也是可以支持的。 …...

【docker】网络模式管理
目录 一、Docker网络实现原理 二、Docker的网络模式 1、host模式 1.1 host模式原理 1.2 host模式实操 2、Container模式 2.2 container模式实操 3、none模式 4、bridger模式 4.1 bridge模式的原理 4.2 bridge实操 5、overlay模式 6、自定义网络模式 6.1 为什么需要…...
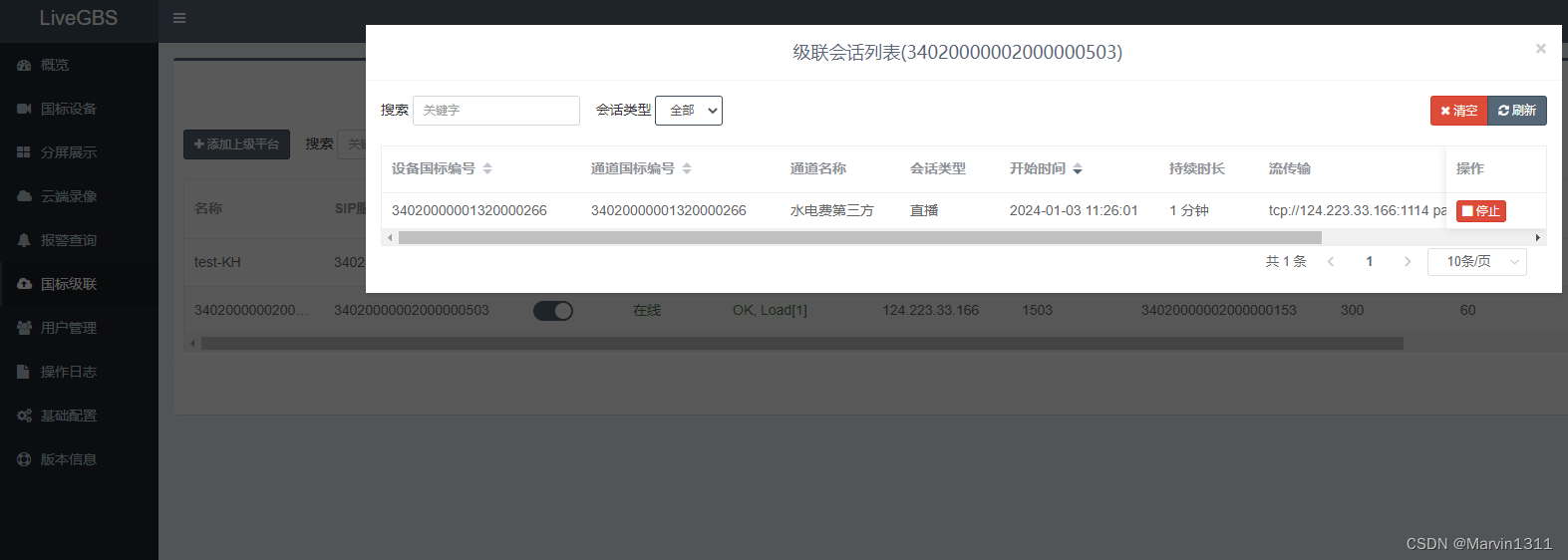
LiveGBS国标GB/T28181流媒体平台功能-国标级联中作为下级平台对接海康大华宇视华为政务公安内网等GB28181国标平台查看级联状态及会话
LiveGBS国标级联中作为下级平台对接海康大华宇视华为政务公安内网等GB28181国标平台查看级联状态及会话 1、GB/T28181级联是什么2、搭建GB28181国标流媒体平台3、获取上级平台接入信息3.1、如何提供信息给上级3.2、上级国标平台如何添加下级域3.2、接入LiveGBS示例 4、配置国标…...

技术发展驱动编程语言走向
未来编程语言的走向可能会受到多种因素的影响,包括技术进步、市场需求、开发人员的偏好和生态系统的演变等。以下是一些可能的发展趋势: 简洁性和易用性 随着技术的进步,编程语言可能会变得越来越简洁和易于使用。一些语言可能会引入更高级的…...
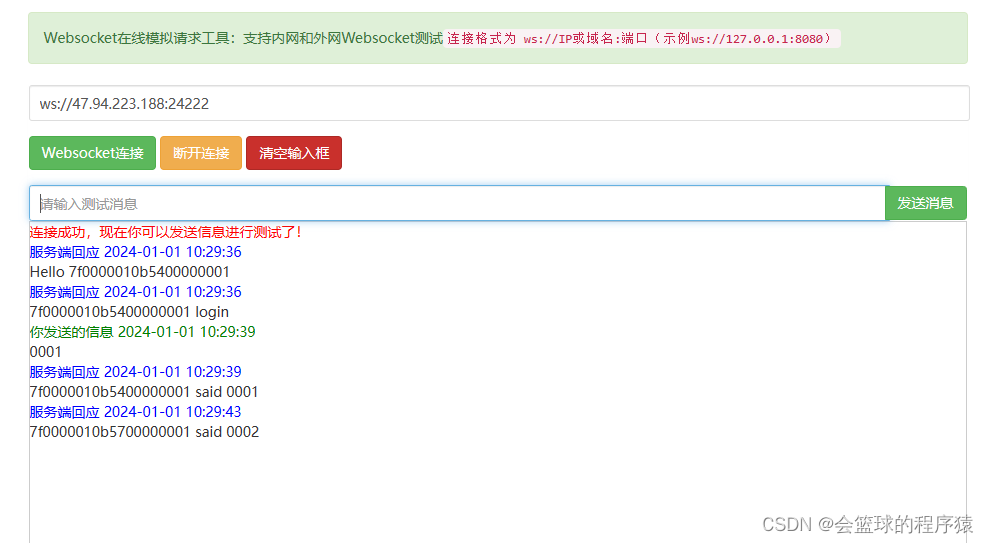
tp5+workman(GatewayWorker) 安装及使用
一、安装thinkphp5 1、宝塔删除php禁用函数putenv、pcntl_signal_dispatch、pcntl_wai、pcntl_signal、pcntl_alarm、pcntl_fork,执行安装命令。 composer create-project topthink/think5.0.* tp5 --prefer-dist 2、配置好站点之后,浏览器打开访问成…...

vscode安装Prettier插件,对vue3项目进行格式化
之前vscode因为安装了Vue Language Features (Volar)插件,导致Prettier格式化失效,今天有空,又重新设置了一下 1. 插件要先安装上 2. 打开settings.json {"editor.defaultFormatter": "esbenp.prettier-vscode","…...

macOS跨进程通信: XPC 创建实例
一:简介 XPC 是 macOS 里苹果官方比较推荐和安全的的进程间通信机制。 集成流程简单,但是比较绕。 主要需要集成 XPC Server 这个模块,这个模块最终会被 apple 的根进程 launchd 管理和以独立进程的方法唤起和关闭, 我们主app 进…...

Ubuntu18.04 升级Ubuntu20.04
文章目录 背景升级方法遇到的问题 背景 因项目环境需要,欲将Ubuntu18.04升级至Ubuntu20.04,参考网上其他小伙伴的方法,也遇到了一个问题,特此记录一下,希望能帮助其他有同样问题的小伙伴。 升级方法 参考:…...
自动化测试怎么做?看完你就懂了。。。
前言 我想应该有很多测试人员应该有这样的疑虑,自动化测试要怎么去做,现在我把自己的一些学习经验分享给大家,希望对你们有帮助,有说的不好的地方,还请多多指教! 对于测试人员来说,不管进行功…...

小秋SLAM入门实战opencv所有文章汇总
opencv_core和 opencv_imgcodecs是 OpenCV(开源计算机视觉库)的两个主要模块 【如何使用cv::erode()函数对图像进行腐蚀操作】 头文件用途 用OpenCV创建一张类型为CV_8UC1的单通道随机灰度图像 用OpenCV创建一张灰度黑色图像并设置某一列为白色 OpenCV创…...

2023年终总结(脚踏实地,仰望星空)
回忆录 2023年,经历非常多的大事情,找工作、实习、研究生毕业、堂哥结婚、大姐买车、申博、读博、参加马拉松,有幸这一年全家人平平安安,在稳步前进。算是折腾的一年,杭州、赣州、武汉、澳门、珠海、遵义来回跑。完成…...

Transforer逐模块讲解
本文将按照transformer的结构图依次对各个模块进行讲解: 可以看一下模型的大致结构:主要有encode和decode两大部分组成,数据经过词embedding以及位置embedding得到encode的时输入数据 输入部分 embedding就是从原始数据中提取出单词或位置&…...

macOS进程间通信的常用技术汇总
macOS进程间通信的常用技术汇总 命令行传参。yyds管道(pipe), 匿名管道, c的技术,可以跨平台使用 只能在父子进程间通信,由于是单向的管道,只能单方面传输数据。 如果需要双向传输,需要建立双向的两条管道才行 匿名管…...

高德地图信息窗体设置
1. 添加默认信息窗体 //构建信息窗体中显示的内容var info [];info.push(<div style"height: 36px; line-height: 45px; padding: 0px 20px; white-space:nowrap;">位置:北京</div>);info.push(<div style"height: 36px; line-heig…...
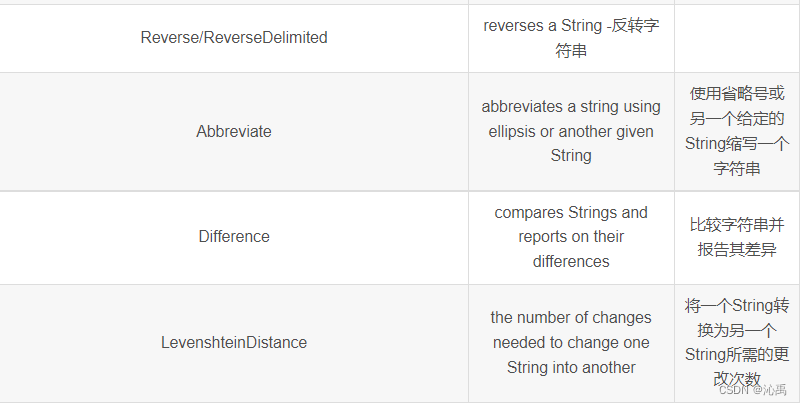
isEmpty 和 isBlank 的用法区别,居然一半的人答不上来.....
isEmpty 和 isBlank 的用法区别 isEmpty系列isBank系列 hi!我是沁禹~ 也许你两个都不知道,也许你除了isEmpty/isNotEmpty/isNotBlank/isBlank外,并不知道还有isAnyEmpty/isNoneEmpty/isAnyBlank/isNoneBlank的存在, come on ,让我们一起来探索org.apache…...

数据分析求职-简历准备
简历在整个求职过程中的重要性不言而喻,今天咱们来聊求职过程中简历准备的那些事儿~ 1. 简历究竟有啥用 求职的流程简单说就是:网申->笔试->面试->offer 其中网申环节,简历100%决定了你的通过与否,这个点大家都知道。…...
亚马逊店铺遇到账号申诉模版分享
1.表达诚意,先认错再说:我知道,最近我们在Amazon.com上作为卖家的表现已经低于亚马逊和我们自己的质量标准。 2.清楚分明的格式:我们库存管理的混乱导致了延迟发货,更糟糕的是,物品无法使用。当延迟发货和…...

2023年广东省网络安全A模块(笔记详解)
模块A 基础设施设置与安全加固 一、项目和任务描述: 假定你是某企业的网络安全工程师,对于企业的服务器系统,根据任务要求确保各服务正常运行,并通过综合运用登录和密码策略、流量完整性保护策略、事件监控策略、防火墙策略等多…...
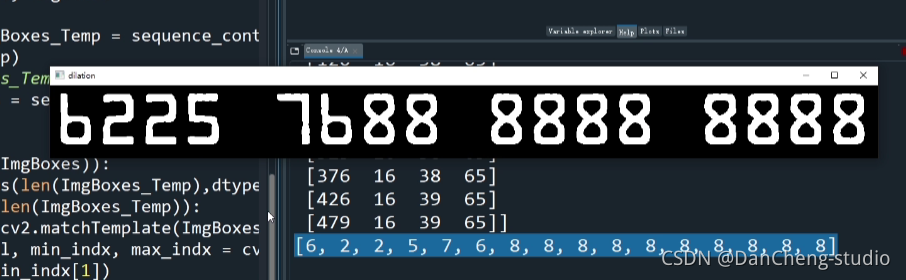
竞赛保研 基于机器视觉的银行卡识别系统 - opencv python
1 前言 🔥 优质竞赛项目系列,今天要分享的是 基于深度学习的银行卡识别算法设计 该项目较为新颖,适合作为竞赛课题方向,学长非常推荐! 🧿 更多资料, 项目分享: https://gitee.com/dancheng…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

ThreadLocal 源码
ThreadLocal 源码 此类提供线程局部变量。这些变量不同于它们的普通对应物,因为每个访问一个线程局部变量的线程(通过其 get 或 set 方法)都有自己独立初始化的变量副本。ThreadLocal 实例通常是类中的私有静态字段,这些类希望将…...

MLP实战二:MLP 实现图像数字多分类
任务 实战(二):MLP 实现图像多分类 基于 mnist 数据集,建立 mlp 模型,实现 0-9 数字的十分类 task: 1、实现 mnist 数据载入,可视化图形数字; 2、完成数据预处理:图像数据维度转换与…...
