java数据结构与算法刷题-----LeetCode70. 爬楼梯
| java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 |
|---|
很多人觉得动态规划很难,但它就是固定套路而已。其实动态规划只不过是将多余的步骤,提前放到dp数组中(就是一个数组,只不过大家都叫它dp),达到空间换时间的效果。它仅仅只是一种优化思路,因此它目前的境地和线性代数一样----虚假的难。
- 想想线性代数,在国外留学的学生大多数不觉得线性代数难理解。但是中国的学生学习线性代数时,完全摸不着头脑,一上来就是行列式和矩阵,根本不知道这玩意是干嘛的。
- 线性代数从根本上是在空间上研究向量,抽象上研究线性关系的学科。人家国外的教科书都是第一讲就帮助大家理解研究向量和线性关系。
- 反观国内的教材,直接把行列式搞到第一章。搞的国内的学生在学习线性代数的时候,只会觉得一知半解,觉得麻烦,完全不知道这玩意学来干什么。当苦尽甘来终于理解线性代数时干什么的时候,发现人家国外的教材第一节就把这玩意讲清楚了。你只会大骂我们国内这些教材,什么狗东西(以上是自己学完线性代数后的吐槽,我们同学无一例外都这么觉得)。
而我想告诉你,动态规划和线性代数一样,我学完了才知道,它不过就是研究空间换时间,提前将固定的重复操作规划到dp数组中,而不用暴力求解,从而让效率极大提升。
- 但是网上教动态规划的兄弟们,你直接给一个动态方程是怎么回事?和线性代数,一上来就教行列式和矩阵一样,纯属恶心人。我差不多做了30多道动态规划题目,才理解,动态方程只是一个步骤而已,而这已经浪费我很长时间了,我每道题都一知半解不理解,过程及其痛苦。最后只能重新做。
- 动态规划,一定是优先考虑重复操作与dp数组之间的关系,搞清楚后,再提出动态方程。而你们前面步骤省略了不讲,一上来给个方程,不是纯属扯淡吗?
- 我推荐研究动态规划题目,按5个步骤,从上到下依次来分析
- DP数组及下标含义
- 递推公式
- dp数组初始化
- 数组遍历顺序(双重循环及以上时,才考虑)
- dp数组打印,分析思路是否正确(相当于做完题,检查一下)
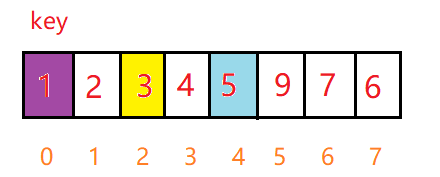
| 拿到比较抽象的题,先列出前几项结果,尝试看出问题的本质(很多比较抽象的题,本质都很简单,抓住问题的本质,那么可以做到解决1道题,扩展到解决一类问题) |
|---|
- n = 0时:结果为0
- n = 1时:结果为1
- n = 2时:结果为2
- n = 3时:结果为3
- n = 4时:结果为5
可见 这道题的规律0 1 2 3 5… 和斐波那契数列的0 1 1 2 3 5…非常像
| 什么是斐波那契数列? |
|---|
- 斐波那契数列:第一个值是0,第二个值是1,剩下的元素是它前两个元素和,例如:0 1 1 2 3 5… , 可见除了最开始的两个固定为0和1外,其余每一个元素都是前两个元素的和。
- 也就是说,这玩意一看就是固定的一套值,如果每次都重新生成,就太暴力了。
- 动态规划的思想就是,将生成的过程,就生成一次,之后再用,直接从dp数组中拿。从而大大提升效率
| 解题思路 |
|---|
- 暴力求解的思想,就是定义3个或者2个变量,然后累加,以获得指定位置的斐波那契数。每次都需要从头开始累加
- 但是如果我们预先将其存储到dp数组,就可以直接通过dp[x], 获取dp数组中指定位置x的对应斐波那契数,而不用每次都从头计算。
- 但是这道题,从第4个元素开始,才符合斐波那契数列的规则,因此我们这道题,可以用斐波那契数列思想,但不能照搬
- 可见这道题,前3个为固定值 0 1 2 ,剩下的都是当前元素的前两项的和。
| 动态规划思考5步曲 |
|---|
- DP数组及下标含义
DP数组存储我们分析的
类似斐波那契数列的数列,这个数列是一维线性的,所以只需一维数组存储。下标代表数在数列中的位置。dp[0] = 0,dp[1] = 1,dp[2]=2是头三个固定值(斐波那契数列头两个是固定值),dp[3]开始,每个元素是前两个数组元素的和。即可生成对应数列的dp数组。
- 递推公式
既然知道了DP数组就是存储的
类似斐波那契数列的数列,那么递推公式,很显然就是当前元素=前两个元素的和。F(n) = F(n-1)+F(n-2)。 而且F(0) = 0,F(1)=1,F(2) = 2这是这个数列的特性,前三个值固定为0,1,2.
- dp数组初始化
- 数组遍历顺序(因为这个数列是一维的,只需要一重循环,无需考虑这个)
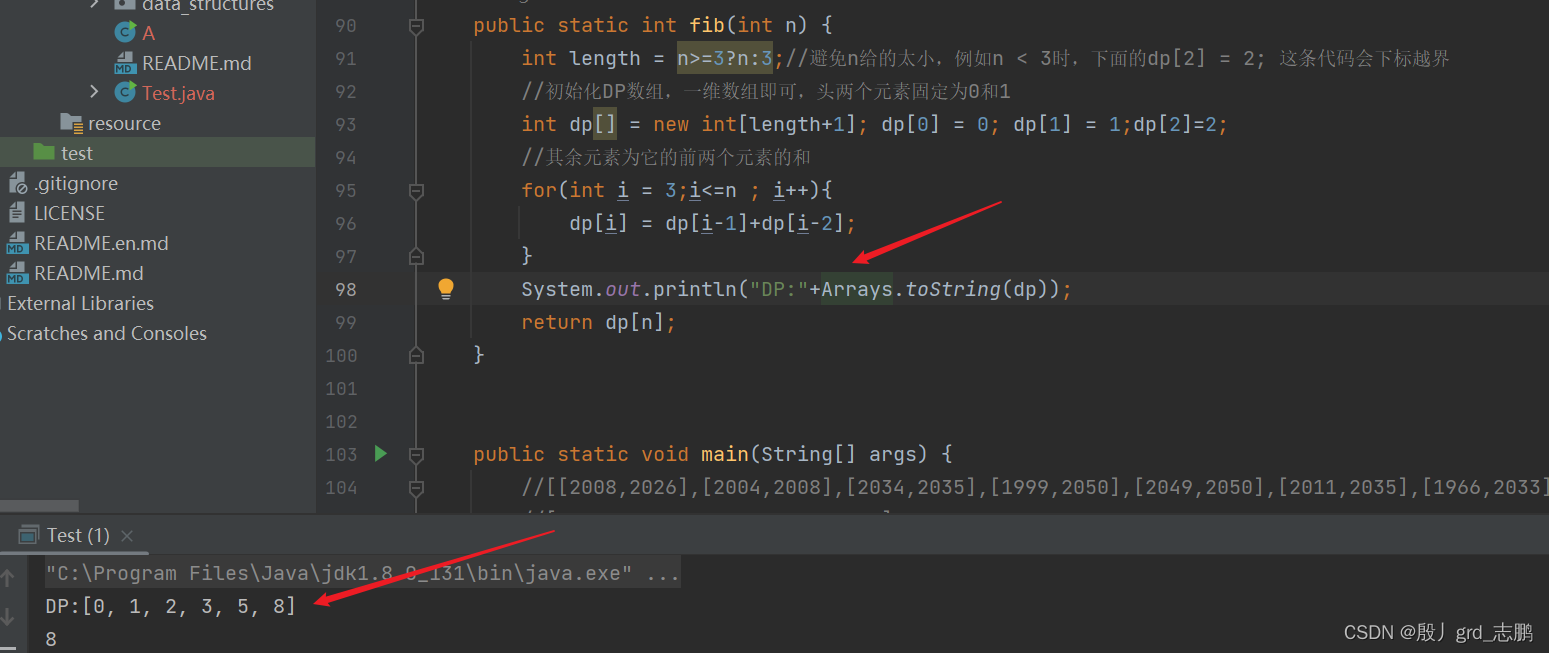
- 打印dp数组(自己生成dp数组后,将dp数组输出看看,是否和自己预想的一样。)
| 代码 |
|---|
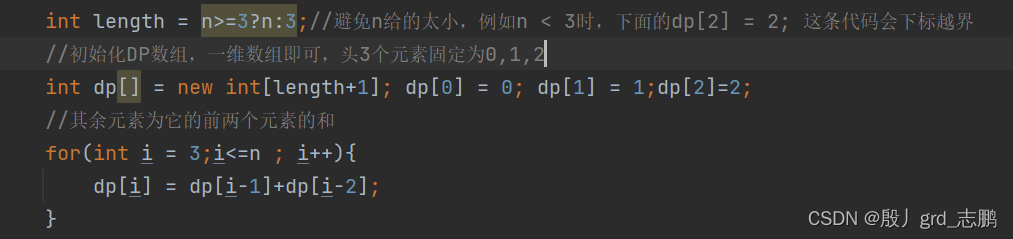
class Solution {public int climbStairs(int n) {int length = n>=3?n:3;//避免n给的太小,例如n < 3时,下面的dp[2] = 2; 这条代码会下标越界//初始化DP数组,一维数组即可,头3个元素固定为0,1,2int dp[] = new int[length+1]; dp[0] = 0; dp[1] = 1;dp[2]=2;//其余元素为它的前两个元素的和for(int i = 3;i<=n ; i++){dp[i] = dp[i-1]+dp[i-2];}return dp[n];}
}
相关文章:
java数据结构与算法刷题-----LeetCode70. 爬楼梯
java数据结构与算法刷题目录(剑指Offer、LeetCode、ACM)-----主目录-----持续更新(进不去说明我没写完):https://blog.csdn.net/grd_java/article/details/123063846 很多人觉得动态规划很难,但它就是固定套路而已。其实动态规划只…...
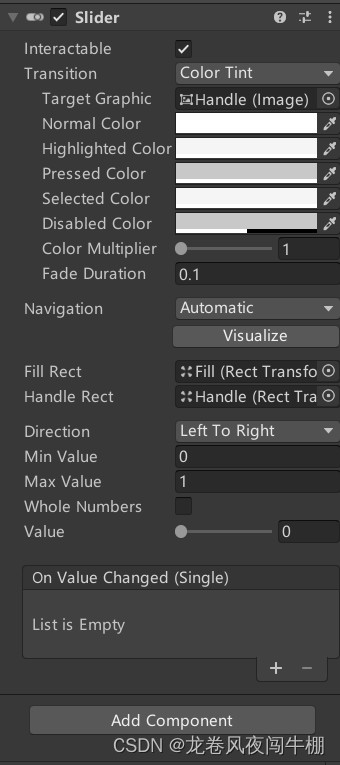
【Unity入门】UGUI之Slider(滑动条)
目录 一、什么是Slider?二、Slider属性与功能 一、什么是Slider? Slider控件允许用户可以通过鼠标来在预先确定的范围调节数值 我们可以在Hierarchy视图右键 -> UI ->Slider来创建滑动条 通过上图可以发现Unity内置的Slider主要有3部分&#x…...

MySQL中UNION和UNION ALL的区别有哪些?
在MySQL中如何想要对两个结果集进行合并操作,可以使用UNION和UNION ALL,如果只是想要去除掉重复的记录,属于UNION ALL 即可,但是如何想要除掉没有重复行数据,就要使用Union。本文详细向大家介绍MySQL中UNION和UNION AL…...
Android kotlin build.gradle.kts配置
1. 添加 maven 仓库 1. 1. settings配置 1. 1.1. settings.gradle repositories {maven {url https://maven.aliyun.com/repository/public/}mavenCentral() }1. 1.2. settings.gradle.kts repositories {maven {setUrl("https://maven.aliyun.com/repository/public/…...

css、js、vue常考部分面试题
css css盒子水平垂直居中方法 方法一:定位 .child{height: 100px;position: absolute;//父元素相对定位top:50%;left:50%;transform: translate(-50%,-50%); } 方法二:定位 .child{width: 100px;height: 100px;position: absolute;top:50%;left:50%…...

OpenAI ChatGPT-4开发笔记2024-03:Chat之Function Calling/Function/Tool/Tool_Choice
Updates on Function Calling were a major highlight at OpenAI DevDay. In another world,原来的function call都不再正常工作了,必须全部重写。 function和function call全部由tool和tool_choice取代。2023年11月之前关于function call的代码都准备翘翘。 干嘛…...
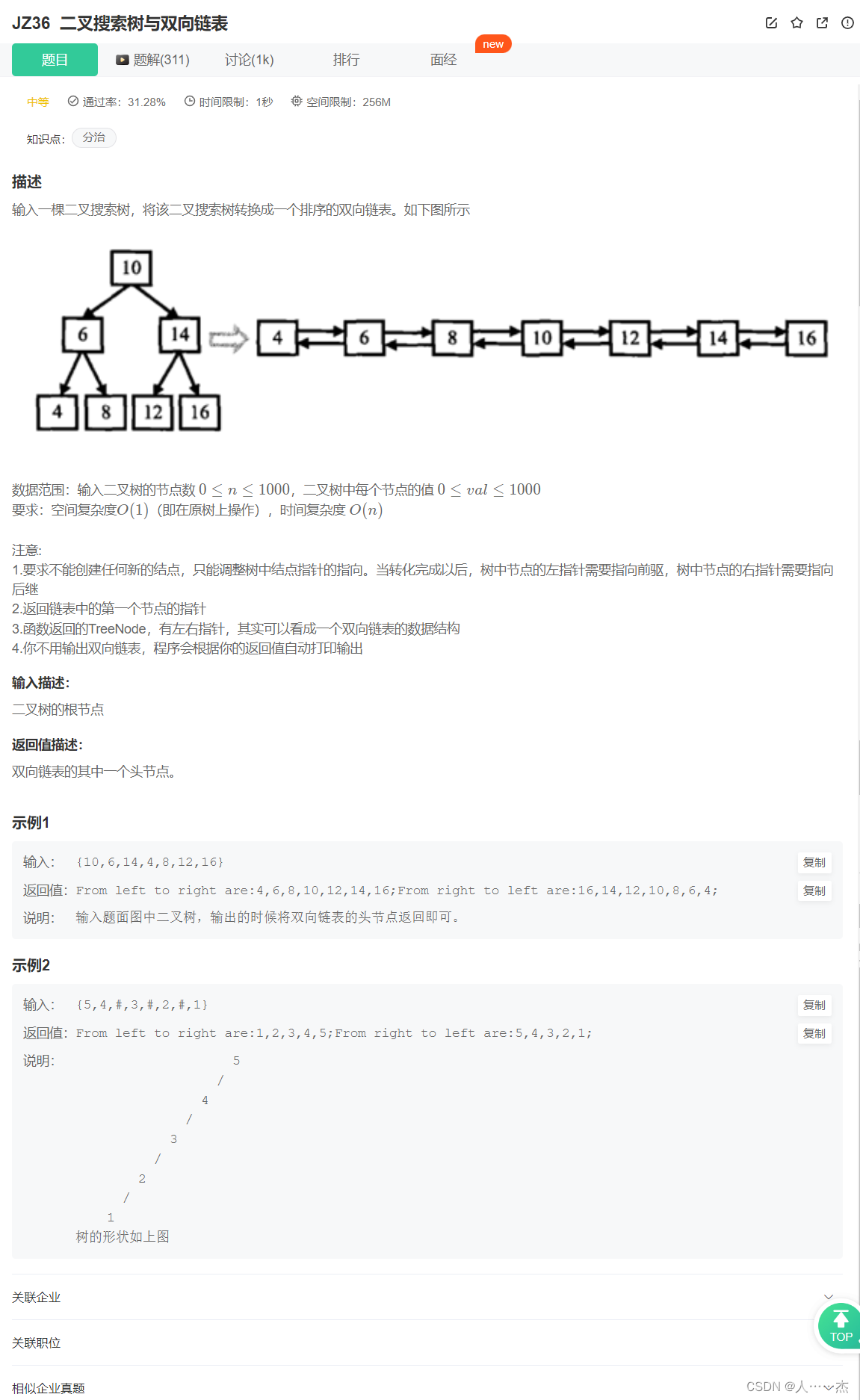
二叉搜索树与双向链表
解题思路一: /** public class TreeNode {int val 0;TreeNode left null;TreeNode right null;public TreeNode(int val) {this.val val;} } */ // 一定要用自己的理解真正弄出来才行,否则没有用! // 再次提醒,计算机这种工科…...

uniapp中组件库的Checkbox 复选框 的丰富使用方法
目录 #平台差异说明 #基本使用 #自定义形状 #禁用checkbox #自定义形状 #自定义颜色 #横向排列形式 #横向两端排列形式 API #Checkbox Props #CheckboxGroup Props #CheckboxGroup Event 复选框组件一般用于需要多个选择的场景,该组件功能完整ÿ…...
Spring Cloud + Vue前后端分离-第10章 基于阿里云OSS的文件上传
源代码在GitHub - 629y/course: Spring Cloud Vue前后端分离-在线课程 Spring Cloud Vue前后端分离-第10章 基于阿里云OSS的文件上传 前面介绍的文件上传是基于本地文件服务器的文件上传,但是自己搭文件服务器会有很多运维的问题,比如磁盘满了要扩容…...

C++ 中的耗时计算函数
#include <time.h>int clock_gettime (clockid_t clock_id, struct timespec *tp) 获取当前 clock_id 的时钟值并存储在 tp 中。 其中 tp 是一个 timespec 结构体,在 time.h 头文件中定义: #include <time.h>:struct timespec {time_t t…...

【Element】el-form和el-table嵌套实现表格编辑并提交表单校验
一、背景 页面需要用到表格采集用户数据,提交时进行表单校验;即表格中嵌套着表单,保存时进行表单校验 二、功能实现 2.1、el-form和el-table嵌套说明 ① :model"formData" 给表单绑定数据,formData是表单的数据对象 …...

初识Winform
什么是winform? WinForms(Windows Forms)是Microsoft .NET框架中的一个用户界面(UI)技术,用于创建Windows应用程序。它提供了一组用于构建图形用户界面的类和控件,以及与用户交互的事件模型。 …...

Redis:原理速成+项目实战——Redis实战5(互斥锁、逻辑过期解决缓存击穿问题)
👨🎓作者简介:一位大四、研0学生,正在努力准备大四暑假的实习 🌌上期文章:Redis:原理速成项目实战——Redis实战4(解决Redis缓存穿透、雪崩、击穿) 📚订阅专…...

前端优化之一:dns预获取 dns-prefetch 提升页面载入速度
问题:怎么做到dns域解析? 用于优化网站页面的图片 问题:怎么提升网站性能? dns域解析,是提升网站的一个办法。 DNS Prefetch,即DNS预获取,是前端优化的一部分。 一般来说,在前端…...

C语言中一些基本数据类型的典型大小
char:通常是1字节。表示一个字符。int:通常在现代系统中是4字节(但这取决于编译器和架构,有时可能是2字节)。float:通常是4字节。double:通常是8字节。short 和 short int:通常是2字…...
[C/C++]排序算法 快速排序 (递归与非递归)
目录 🚩概念: 🚩实现: ⚡1.hoare ⚡2.挖坑法 ⚡3.双指针法 🚩快速排序递归实现 🚩快速排序非递归实现 🚩概念: 通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据比另一部分的所有…...

『年度总结』逐梦编程之始:我的2023学习回顾与展望
目录 前言 我与Python 我与C语言 第一篇正式博客: 第二篇正式博客(扫雷): 指针学习笔记: C语言学习笔记: 我与数据结构: yuan 这篇博客,我将回顾2023年编程之旅的起点,同时展…...
MyBatis学习二:Mapper代理开发、配置文件完成增删改查、注解开发
前言 公司要求没办法,前端也要了解一下后端知识,这里记录一下自己的学习 学习教程:黑马mybatis教程全套视频教程,2天Mybatis框架从入门到精通 文档: https://mybatis.net.cn/index.html Mapper代理开发 目的 解决…...
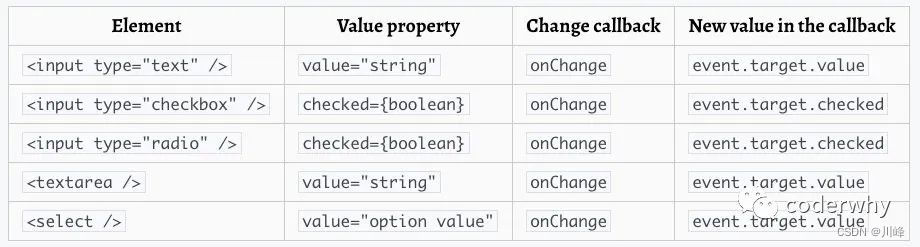
【React系列】受控非受控组件
本文来自#React系列教程:https://mp.weixin.qq.com/mp/appmsgalbum?__bizMzg5MDAzNzkwNA&actiongetalbum&album_id1566025152667107329) 一. refs 的使用 在React的开发模式中,通常情况下不需要、也不建议直接操作DOM原生,但是某些…...
:2D直方图)
OpenCV-Python(22):2D直方图
目标 了解图像的2D直方图绘制2D直方图 介绍 在前面的部分我们介绍了如何绘制一维直方图,之所以称为一维,是因为我们只考虑了图像的一个特征:灰度值。但是在2D 直方图中我们就需要考虑两个图像特征。对于彩色图像的直方图通常情况下我们需要…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...