OSI 模型和 TCP/IP 模型的异同
开放式系统互联模型(OSI)是一个参考标准,解释协议相互之间应该如何相互作用。TCP/IP协议是美国国防部发明的,是让互联网成为了目前这个样子的标准之一
OSI:物理层,数据链路层,网络层,传输层,会话层,表示层,应用层
TCP/IP:网络接口层,网络层,传输层,应用层

相同点:
1.都是分层结构,并且工作方式一样,都要层与层之间很密切的协作关系。有相同的应用层,传输层,网络。
不同点:
1.对于OSI/RM模型有三个明确的核心概念.(1)服务,(2)接口,(3)协议。而TCP/IP对此没有明确的区分
2.OSI 先有模型,后有协议规范,适合于描述各种网络;TCP/IP 是先有协议集然后建立模型,不适用于非 TCP/IP 网络。
3.OSI模型的网络层提供两种服务类型:面向连接的虚电路交换或无连接的数据报交换。而TCP/IP的网络层使用的是IP协议,提供的是无连接的数据报交换。
4.针对传输层,TCP/IP模型在一开始就提出了面向连接和无连接服务,其中TCP协议提供面向连接的可靠数据传输服务,而UDP协议提供无连接的不可靠数据传输服务。相比之下,OSI模型最初只关注面向连接的服务,传输层采用了传输控制协议(TCP)作为标准协议,提供面向连接的可靠数据传输服务。直到很晚才开始制定无连接服务的标准,引入了用户数据报协议(UDP),提供无连接的不可靠数据传输服务。
为什么 TCP/IP 去除了表示层和会话层
OSI 参考模型在提出时,他们的理想是非常好的,但实际上,由于会话层、表示层、应用层都是在应用程序内部实现的,最终产出的是一个应用数据包,而应用程序之间是几乎无法实现代码的抽象共享的,这也就造成 OSI 设想中的应用程序维度的分层是无法实现的,例如,我们几乎不会认为数据的压缩、加密算法算是一种协议,而会话的概念则更为抽象,难以用协议来进行描述,所以在后来的 TCP/IP 协议框架的设计中,便将表示层和会话层与应用层整合在一起,让整个过程更为清晰明了。
总结:会话层,表示层和应用层都是在应用程序内部实现的,应用程序之间无法实现代码的抽象共享,因此应用程序维度无法实现分层。
此段来自:力扣
以上为看资料总结,如有错误,请佬们指出!!
相关文章:

OSI 模型和 TCP/IP 模型的异同
开放式系统互联模型(OSI)是一个参考标准,解释协议相互之间应该如何相互作用。TCP/IP协议是美国国防部发明的,是让互联网成为了目前这个样子的标准之一 OSI:物理层,数据链路层,网络层࿰…...

创新性文生视频模型,南洋理工开源FreeInit
文本领域的ChatGPT,画图领域的Midjourney都展现出了大模型强大的一面,虽然视频领域有Gen-2这样的领导者,但现有的视频扩散模型在生成的效果中仍然存在时间一致性不足和不自然的动态效果。 南洋理工大学S实验室的研究人员发现,扩散…...

linux的页缓存page cache
目录 如何查看系统的 Page Cache? 为什么 Linux 不把 Page Cache 称为 block cache? Page Cache 的优劣势 Page Cache 的优势 加快数据访问 减少 IO 次数,提高系统磁盘 I/O 吞吐量 Page Cache 的劣势 由于我们开发的程序要运行的话一般…...
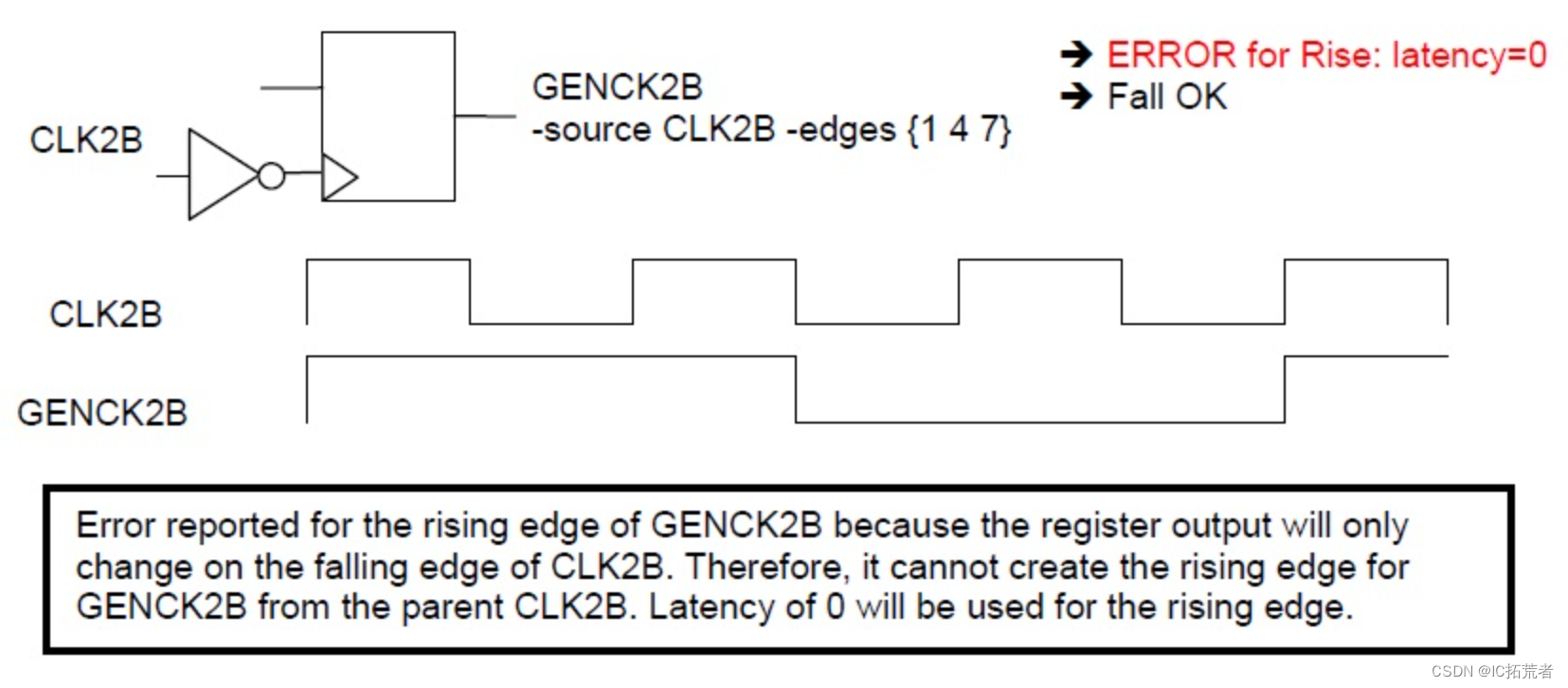
数字IC后端实现之Innovus TA-152错误解析(分频generated clock定义错误)
**ERROR: (TA-152): A latency path from the ‘Fall’ edge of the master clock at source pin… Error Code TA-152 在数字IC后端实现innovus中我们经常会看到这类Error,具体信息如下所示。 Error Message **ERROR: (TA-152): A latency path from the ‘Fa…...
虹科方案丨从困境到突破:TigoLeap方案引领数据采集与优化变革
来源:虹科工业智能互联 虹科方案丨从困境到突破:TigoLeap方案引领数据采集与优化变革 原文链接:https://mp.weixin.qq.com/s/H3pd5G8coBvyTwASNS_CFA 欢迎关注虹科,为您提供最新资讯! 导读 在数字化工厂和智能制造时…...
自检服务器,无需服务器、不用编程。
自检服务器,无需服务器、不用编程。 大家好,我是JavaPub. 这几年自媒体原来热,很多人都知道了个人 IP 的重要性。连一个搞中医的朋友都要要做一个自己的网站,而且不想学编程、还不想花 RMB 租云服务。 老读者都知道,…...
下InheritableThreadLocal引起的问题)
Java并行流parallelStream()下InheritableThreadLocal引起的问题
Java并行流parallelStream()下InheritableThreadLocal引起的问题 引起问题的代码。 List orgs00 Arrays.asList(new Org("aaa"),new Org("bbb"),new Org("aa0"));List orgs orgs00.parallelStream() .map(org -> {// 模拟从数据库中获取 …...

【C++期末编程题题库】代码+详解18道
适合期末复习c看,或者刚入门c的小白看,有的题会补充知识点,期末复习题的代码一般比较简单,所以语法上没那么严谨。本文所有题目要求全在代码块的最上面。 目录 1、设计复数类 2、设计Computer类 3、实现相加的函数模板 4、圆类…...

一种DevOpts的实现方式:基于gitlab的CICD(一)
写在之前 笔者最近准备开始入坑CNCF毕业的开源项目,看到其中有一组开源项目的分类就是DevOpts。这个领域内比较出名的项目是Argocd,Argo CD 是一个用于 Kubernetes 的持续交付 (Continuous Delivery) 工具,它以声明式的方式实现了应用程序的…...

nodejs和vuejs的区别
一、vue项目开发中,两个经常混合使用。 不同: 1、概念不同: 一个是前端框架,一个是服务端语言。 Node.js 是一个基于 Chrome V8 引擎的 JavaScript 运行环境。 Node.js 使用了一个事件驱动、非阻塞式 I/O 的模型,使…...

16、Kubernetes核心技术 - 节点选择器、亲和和反亲和
目录 一、概述 二、节点名称 - nodeName 二、节点选择器 - nodeSelector 三、节点亲和性和反亲和性 3.1、亲和性和反亲和性 3.2、节点硬亲和性 3.3、节点软亲和性 3.4、节点反亲和性 3.5、注意点 四、Pod亲和性和反亲和性 4.1、亲和性和反亲和性 4.2、Pod亲和性/反…...
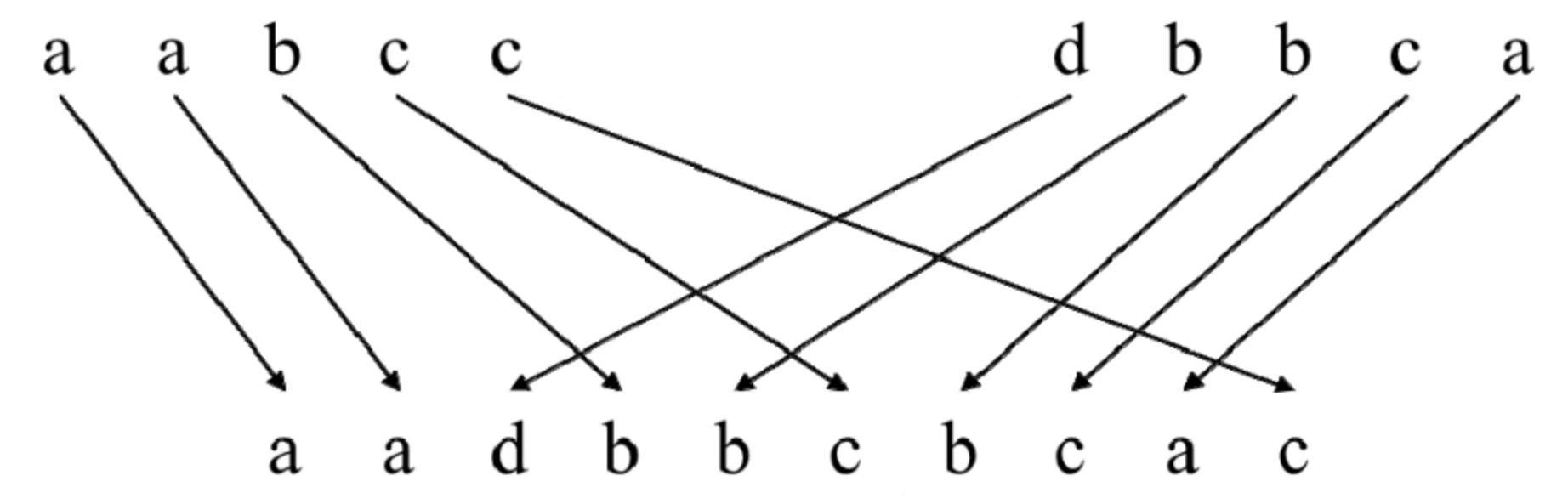
面试算法96:字符串交织
题目 输入3个字符串s1、s2和s3,请判断字符串s3能不能由字符串s1和s2交织而成,即字符串s3的所有字符都是字符串s1或s2中的字符,字符串s1和s2中的字符都将出现在字符串s3中且相对位置不变。例如,字符串"aadbbcbcac"可以由…...
?如何实现数据的双向绑定?)
什么是Vue.js的响应式系统(reactivity system)?如何实现数据的双向绑定?
Vue.js的响应式系统是指一种能够跟踪数据变化并实时更新相关界面的机制。它是Vue.js框架的核心特性之一。 在Vue.js中,你可以使用数据绑定语法将数据绑定到DOM元素上。当绑定的数据发生变化时,Vue.js会自动监听这些变化并更新相关的DOM元素。 Vue.js实…...

力扣labuladong一刷day52天LRU算法
力扣labuladong一刷day52天LRU算法 文章目录 力扣labuladong一刷day52天LRU算法概念一、146. LRU 缓存思路一:使用双向链表加map来手动实现。思路二:使用LinkedHashMap 概念 LRU的全称为Least Recently Used,翻译出来就是最近最少使用的意思…...
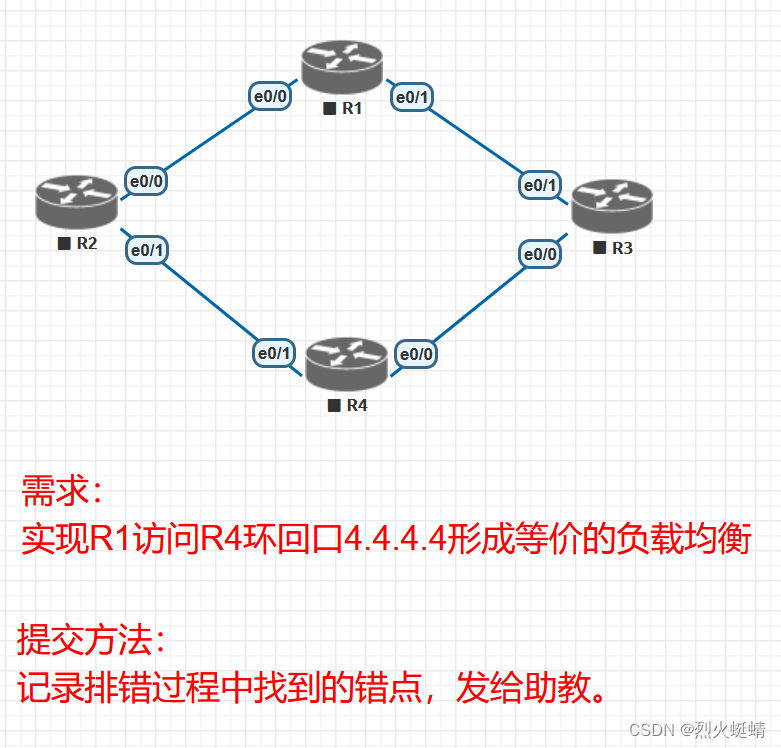
CCNP课程实验-06-EIGRP-Trouble-Shooting
目录 实验条件网络拓朴 环境配置开始排错错误1:没有配置IP地址,IP地址宣告有误错误2:R3配置了与R1不同的K值报错了。错误3:R4上的AS号配置错,不是1234错误4:R2上配置的Key-chain的R4上配置的Key-chain不一致…...
判断完全数-第11届蓝桥杯省赛Python真题精选
[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第27讲。 判断完全数&#…...

【Bootstrap5学习 day12】
Bootstrap5 导航 Bootstrap5提供了一种简单快捷的方法来创建基本导航,它提供了非常灵活和优雅的选项卡和Pills等组件。Bootstrap5的所有导航组件,包括选项卡和Pillss,都通过基本的.nav类共享相同的基本标记和样式。 创建基本导航 要创建简单…...

算法训练第五十九天|503. 下一个更大元素 II、42. 接雨水
503. 下一个更大元素 II: 题目链接 给定一个循环数组 nums ( nums[nums.length - 1] 的下一个元素是 nums[0] ),返回 nums 中每个元素的 下一个更大元素 。 数字 x 的 下一个更大的元素 是按数组遍历顺序,这个数字之…...
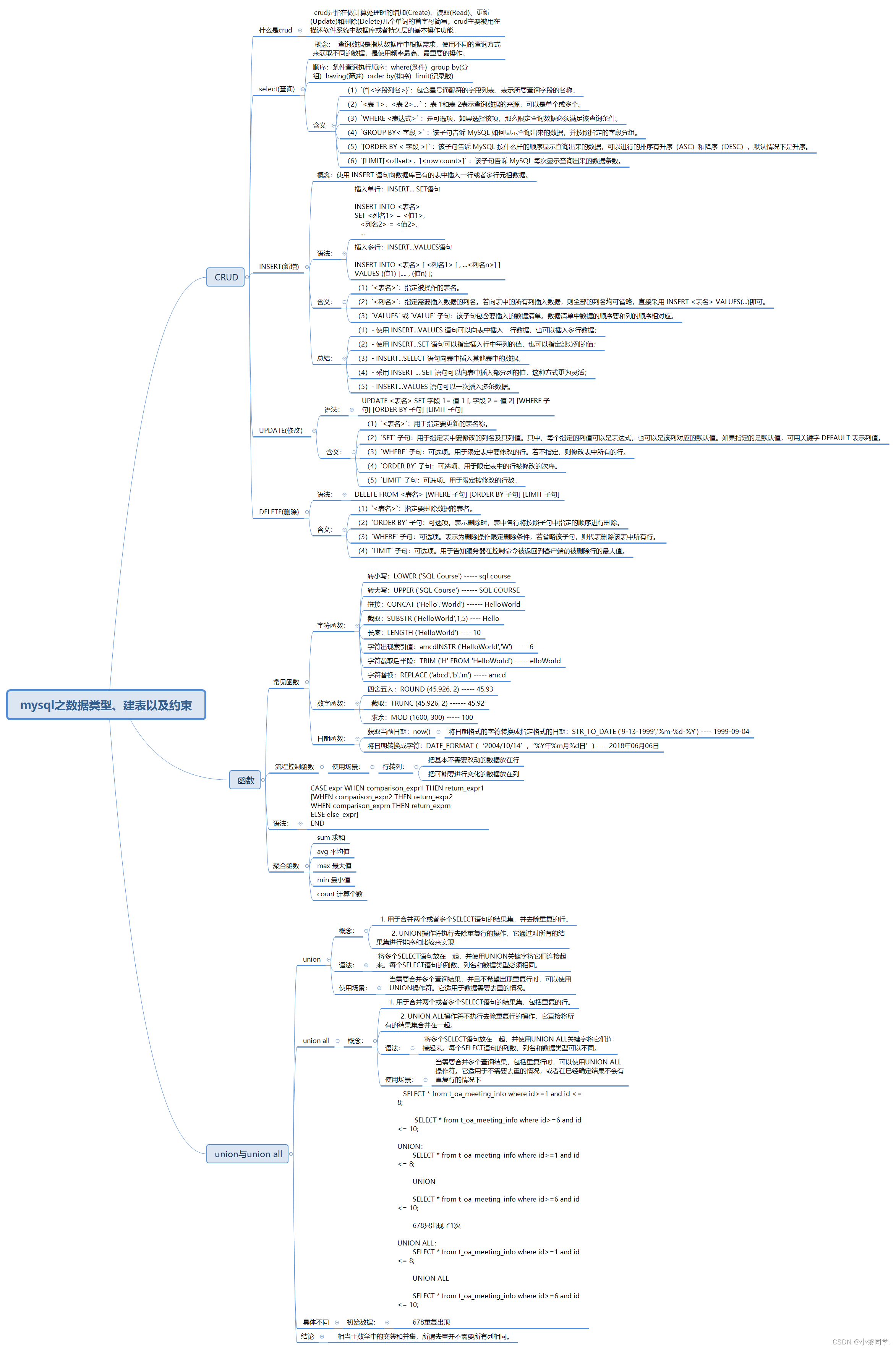
mysql之数据类型、建表以及约束
目录 一. CRUD 1.1 什么是crud 1.2 select(查询) 1.3 INSERT(新增) 1.4 UPDATE(修改) 1.5 DELETE(删除) 二. 函数 2.1 常见函数 2.2 流程控制函数 2.3聚合函数 三. union与union all 3.1 union 3.2 union all 3.3 具体不同 3.4 结论 四、思维导图 一. CRUD 1.1…...
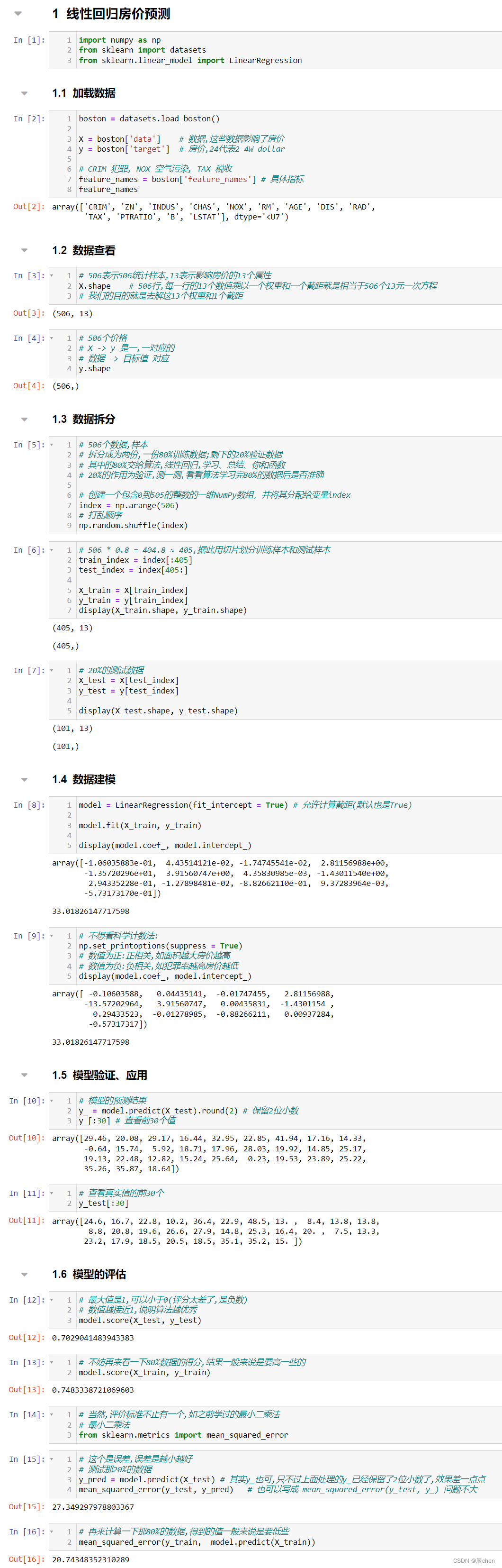
复试 || 就业day04(2024.01.05)项目一
文章目录 前言线性回归房价预测加载数据数据查看数据拆分数据建模模型的验证、应用模型的评估 总结 前言 💫你好,我是辰chen,本文旨在准备考研复试或就业 💫本文内容来自某机构网课,是我为复试准备的第一个项目 &#…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...
