机器学习--回归算法
🌳🌳🌳小谈:一直想整理机器学习的相关笔记,但是一直在推脱,今天发现知识快忘却了(虽然学的也不是那么深),但还是浅浅整理一下吧,便于以后重新学习。
📙参考:ysu期末复习资料和老师的课件
1.回归问题
回归分析用于预测输入变量(自变量)和输出变量(因变量)之间的关系,特别是当输入变量的值发生变化时,输出变量值随之发生变化。
🍀理解:直观来说回归问题等价于函数拟合,选择一条函数曲线使其很好地拟合已知数据且很好地预测未知数据。
回归分析根据自变量个数可分为一元回归分析与多元回归分析。

2.一元线性回归
线性回归算法假设特征和结果满足线性关系。
这就意味着可以将输入项分别乘以一些常量,再与偏置项相加得到输出。
一元线性回归指的是分析只有一个自变量x与因变量y线性相关关系的方法。
过程如下:

举个例子:
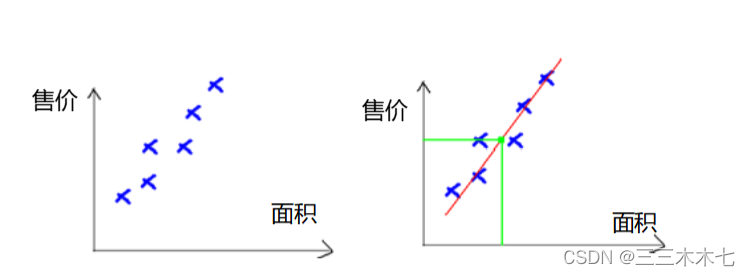
左图是以面积为X轴,售价为Y轴建立房屋销售数据的特征空间表示图。
回归分析是:用一条曲线去尽量准的拟合这些数据,然后如果有新的输入过来,我们可以在将曲线上这个点对应的值返回。
3.一元线性回归求解方法
3.1 最小二乘法
最小二乘法的主要思想:就是求解未知参数,使得理论值与观测值之差(即误差,或者说残差)的平方和达到最小。
【所谓最小二乘,其实也可以叫做最小平方和,其目的就是通过最小化误差的平方和,使得拟合对象无限接近目标对象。】
缺点:最小二乘法主要针对于线性函数,有全局最优解且是闭式解,针对更加复杂的函数难起作用
3.2 梯度下降法
梯度下降法是用来计算函数最小值的。
根据计算一次目标函数梯度的样本数量可分为批量梯度下降(Batch graduebt descent, BGD),随机梯度下降(Stochatic gradient decent, SGD),小批量梯度下降(mini-batch gradient descent)。
(1)批量梯度下降 BGD
在训练过程中,每一步迭代都使用训练集的所有内容。
也就是说,利用现有参数对训练集中的每一个输入生成一个估计输出y ̂_i,然后跟实际输出 y_i 比较,统计所有误差,求平均以后得到平均误差,以此来作为更新参数的依据。
优点:由于每一步都利用了训练集中的所有数据,因此当损失函数达到最小值以后,能够保证此时计算出的梯度为0,换句话说,就是能够收敛。因此,使用BGD时不需要逐渐减小学习速率。
缺点:由于每一步都要使用所有数据,因此随着数据集的增大,运行速度会越来越慢.
(2)随机梯度下降 SGD
随机梯度下降方法一次只抽取一个随机样本进行目标函数梯度计算。
优点:由于每次只计算一个样本,所以SGD收敛非常快。
缺点:因为是随机抽取样本,因此误差是不可避免的,且每次迭代的梯度受抽样的影响比较大。
(3)小批量梯度下降 mini-batch GD
小批量梯度下降结合了批量梯度下降和随机梯度下降的优点,它一次以小批量的训练数据计算目标函数的权重并更新参数。
🌍梯度下降法的问题
1. 难以选择合适的学习速率:如果学习速率选择过小会造成网络收敛太慢,但是设得太大可能使得损失函数在最小点周围不断摇摆而永远达不到最小点;
2.如果训练数据十分稀疏并且不同特征的变化频率差别很大,这时候对变化频率慢得特征采用大的学习率,而对变化频率快的特征采用小的学习率是更好的选择;
3.3 梯度下降改进
(1)Momentum
若当前的梯度方向与累积的历史梯度方向一致,则当前的梯度会被加强,从而这一步下降的幅度更大。若当前的梯度方向与累积的梯度方向不一致,则会减弱当前下降的梯度幅度。
(2)AdaGrad(Adaptive Gradient)
每一次更新参数时(一次迭代),不同的参数使用不同的学习率。
(3)Adam( Adaptive Moment Estimation)
Adam利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。其优点主要在于经过偏置校正后,每一次迭代学习率都有个确定范围,使得参数比较平稳。
4.损失函数
1.平均绝对误差:平均绝对误差MAE(Mean Absolute Error)又被称为l1范数损失(l1-norm loss)
2.平均平方误差:平均平方误差MSE(Mean Squared Error)又被称为l2范数损失(l2-norm loss):
3.均方根差RMSE:是MSE的算术平方根
5.线性回归的改进
5.1 过拟合
过拟合是指模型学习的参数过多,导致拟合的函数完美的预测训练集,但对新数据的测试集预测结果差。
解决办法:
(1)获取更多的数据
(2)数据增强(Data Augmentation)
通过一定规则扩充数据。
(3)使用合适的模型:
减少网络的层数、神经元个数等均可以限制网络的拟合能力;
(4)使用正则项约束模型的权重,降低模型的非线性。
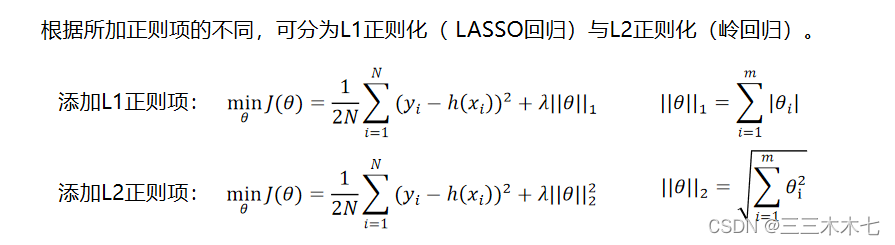
6.项目实战
6.1 波士顿房价
以Scikit-learn的内置数据集波士顿(Boston)房屋价格为案例,采用单变量线性回归算法对数据进行拟合与预测。
波士顿房屋的数据于1978年开始统计,共506个数据点,涵盖了波士顿不同郊区房屋的14种特征信息。
在这里,选取房屋价格(MEDV)、每个房屋的房间数量(RM)两个变量进行回归,其中房屋价格为目标变量,每个房屋的房间数量为特征变量。将数据导入进来,并进行初步分析。
机器学习基本步骤:
数据预处理→特征工程→数据建模→结果评估
详情见:机器学习实践-CSDN博客
🐳自我总结:
项目实践的一般流程是:准备数据→配置网络→训练网络→模型评估→模型预测
配置网络包括:定义网络、定义损失函数、定义优化算法
训练网络:
1. 网络正向传播计算网络输出和损失函数。
2. 根据损失函数进行反向误差传播,将网络误差从输出层依次向前传递, 并更新网络中的参数。
3. 重复1~2步骤,直至网络训练误差达到规定的程度或训练轮次达到设定值。
💬一起加油!
相关文章:
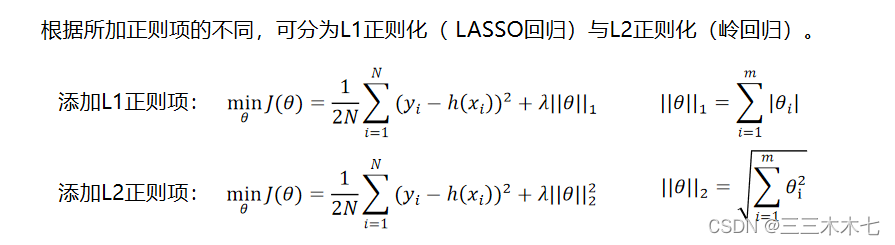
机器学习--回归算法
🌳🌳🌳小谈:一直想整理机器学习的相关笔记,但是一直在推脱,今天发现知识快忘却了(虽然学的也不是那么深),但还是浅浅整理一下吧,便于以后重新学习。 …...

计算机网络——多址复用技术
1. 频分多址(FDMA) 1.1 基本原理 频率分配:在FDMA系统中,整个可用的频带被分割成多个较小的频带或通道。每个通道分配给一个用户。 时间利用:用户在分配给他们的频道上持续进行通信,不受时间限制。 1.2 优…...
stm32 HAL库 4096线ABZ编码器
[TOC]目录 ABZ编码器 4096线 买的是这个 AB相代表计数方向,Z代表过零点 cubemx配置 定时器Encoder 也可以选上DMA 中断 Z相GPIO中断 找一个空闲管脚 打开对应中断 代码 不用DMA int main(void) {short Enc_cnt 0;HAL_TIM_Encoder_Start_IT(&ht…...
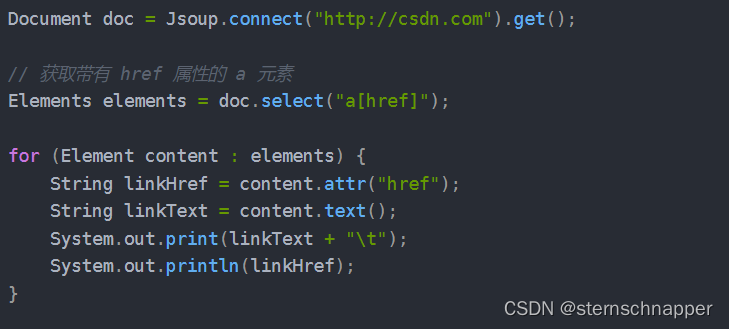
Java爬虫之Jsoup
1.Jsoup相关概念 Jsoup很多概念和js类似,可参照对比理解 Document :文档对象。每份HTML页面都是一个文档对象,Document 是 jsoup 体系中最顶层的结构。 Element:元素对象。一个 Document 中可以着包含着多个 Element 对象&#…...

如何在 C# 12 中使用主构造函数
C# 12 中最引人注目的新功能之一是对主构造函数的支持。主构造函数的概念并不新鲜。包括 Scala、Kotlin 和 OCaml 在内的多种编程语言都支持直接在声明类的位置集成构造函数参数。 在本文中,我们将仔细研究主构造函数以及如何在 C# 12 中使用它们。若要运行本文中提…...
Zookeeper之Java客户端实战
ZooKeeper应用的开发主要通过Java客户端API去连接和操作ZooKeeper集群。可供选择的Java客户端API有: ZooKeeper官方的Java客户端API。第三方的Java客户端API,比如Curator。 接下来我们将逐一学习一下这两个java客户端是如何操作zookeeper的。 1. ZooKe…...

将文本文件导入Oracle数据库的简便方法:SQL Loader Express
需求 我有一个文本文件dbim.txt,是通过alert log生成的,内容如下: 2020-09-11 2020-09-11 ... 2023-12-03 2023-12-03 2023-12-26我已经在Oracle数据库中建立了目标表: create table dbim(a varchar(16));我想把日志文件导入Or…...
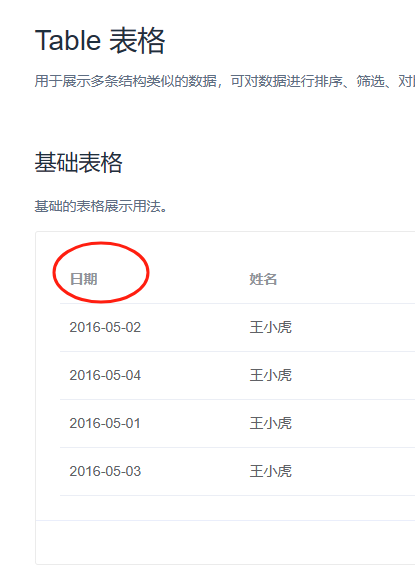
element-ui table-自定义表格某列的表头样式或者功能
自带表格 自定义表格某列的表头样式或者功能 <el-table><el-table-column :prop"date">//自定义表身每行数据<template slot-scope"scope">{{scope.row[scope.column.label] - ? - : scope.row[scope.column.label]}}</template>…...
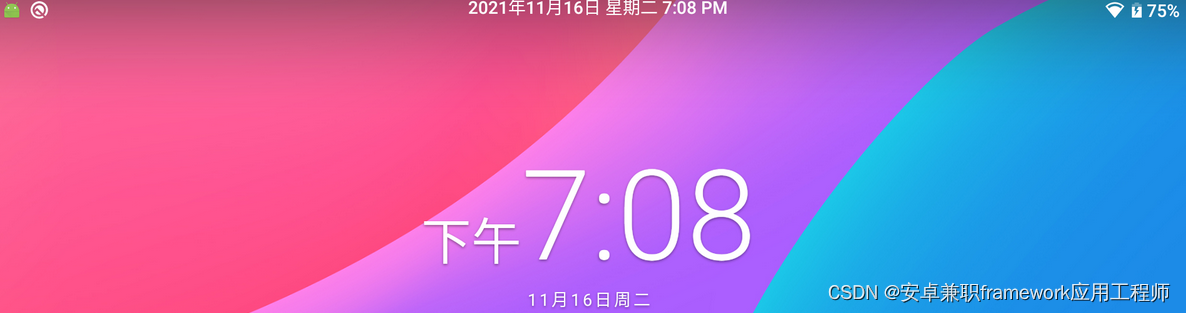
Android 13.0 SystemUI状态栏居中显示时间和修改时间显示样式
1.概述 在13.0的系统rom定制化开发中,在systemui状态栏系统时间默认显示在左边和通知显示在一起,但是客户想修改显示位置,想显示在中间,所以就要修改SystemUI 的Clock.java 文件这个就是管理显示时间的,居中显示的话就得修改布局文件了 效果图如下: 2.SystemUI状态栏居中显…...

讲解eureca和nacus的区别
Eureca和Nacus都是远程过程调用(RPC)框架,用于实现分布式系统中不同节点之间的通信。它们之间的主要区别如下: 架构设计:Eureca是一个基于JavaScript的RPC框架,它使用了WebSockets作为传输层协议。Eureca C…...
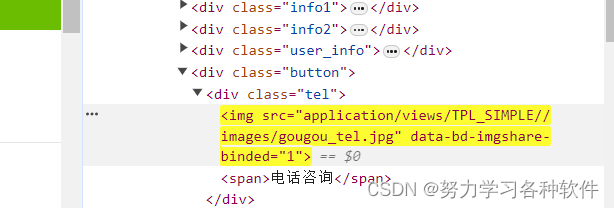
python中parsel模块的css解析
一、爬虫页面分类 1.想要爬取的内容全部在标签中,可以使用xpath去进行解析如下图 2.想要爬取的内容呈现json的数据特征,用.json()转换为字典格式 3.页面不规则,标签中包含大括号,如下面想要获取键值内容怎么做,先用re正…...
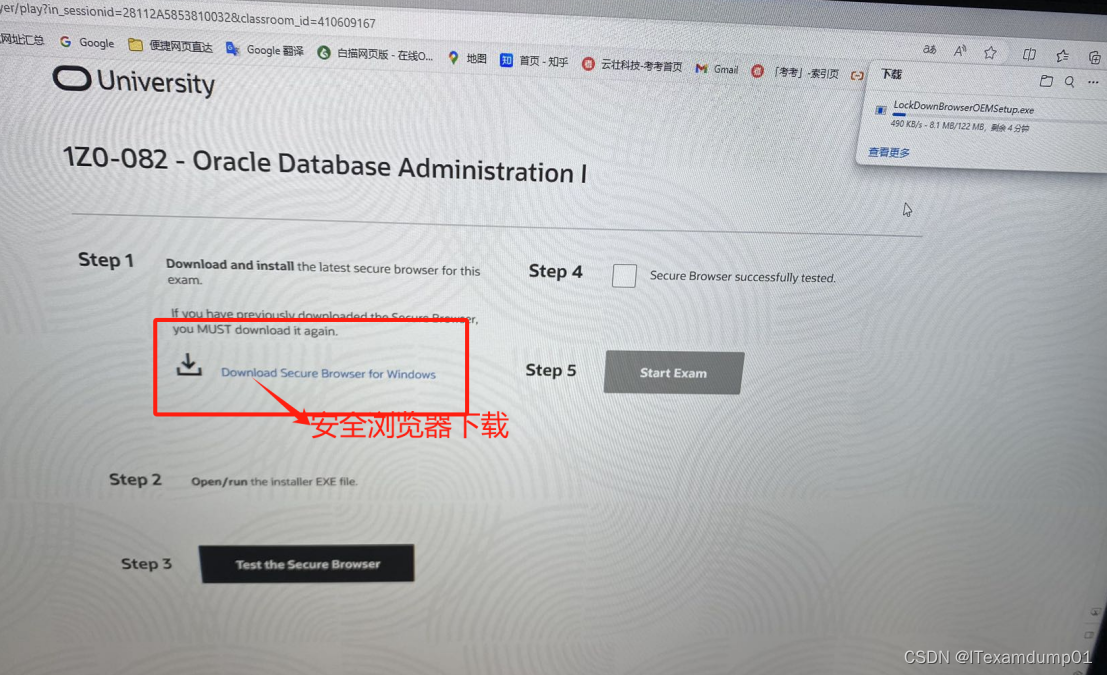
Oracle OCP怎么样线上考试呢
大家好!今天咱们就来聊聊Oracle OCP这个让人又爱又恨的认证。为啥说又爱又恨呢?因为它既是IT界的“金字招牌”,又是一块硬骨头,不是那么容易啃下来的。好了,废话不多说,我们直奔主题,来看看关于…...
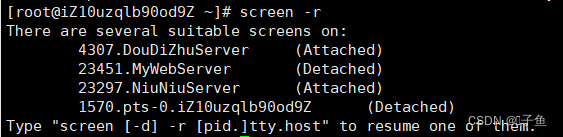
如何让自己的写的程序在阿里云一直运行
购买了阿里云服务器后,每次要用自己写在阿里云的服务器程序都要连接到云端 然后./运行该程序,而且每次一断开终端,该服务器就会自动停止,这样使用相当麻烦。那怎样才能让我们的服务器一直在云端后台运行,即便退出终端…...

【计算机图形学】NAP: Neural 3D Articulation Prior
文章目录 1. 这篇论文做了什么事,有什么贡献?2. Related Work铰接物体建模3D中的Diffusion model扩散模型 3. Pipeline铰接树参数化基于Diffusion的铰接树生成去噪网络 4. 实验评价铰接物体生成——以往做法与本文提出的新指标NAP捕捉到的铰接物体分布质…...

知识付费平台搭建?找明理信息科技,专业且高效
明理信息科技知识付费saas租户平台 在当今数字化时代,知识付费已经成为一种趋势,越来越多的人愿意为有价值的知识付费。然而,公共知识付费平台虽然内容丰富,但难以满足个人或企业个性化的需求和品牌打造。同时,开发和…...

CentOS7部署Kafka
CentOS7部署Kafka 一、部署1、前置条件2、下载与解压3、修改配置4、启动kafka二、使用详解1、创建一个主题2、展示所有主题3、启动消费端接收消息4、生产端发送消息三、代码集成pom.xmlapplication.propertiesKafkaConfiguration.javaKafkaConsumer.javaKafkaProducer.javaVehi…...
JS的防抖和节流
目录 防抖 搜索框带来的问题 实现的思路 案例 封装防抖函数 节流 滚动条加载带来的问题 实现的思路 案例 封装节流函数 防抖 搜索框带来的问题 需求:根据输入框内容来请求数据 <!DOCTYPE html> <html lang"en"> <head><…...
互联网加竞赛 基于人工智能的图像分类算法研究与实现 - 深度学习卷积神经网络图像分类
文章目录 0 简介1 常用的分类网络介绍1.1 CNN1.2 VGG1.3 GoogleNet 2 图像分类部分代码实现2.1 环境依赖2.2 需要导入的包2.3 参数设置(路径,图像尺寸,数据集分割比例)2.4 从preprocessedFolder读取图片并返回numpy格式(便于在神经网络中训练)2.5 数据预…...

pip安装报错SSL
confirming the ssl certificate: HTTPSConnectionPool(hostmirrors.cloud.tencent.com, port443) 错误代码如上 偶然搜索:ubuntu pip出错 confirming the ssl certificate: HTTPSConnectionPool(host‘mirrors.cloud.tencent.com’, port443) 看到这个回答 【日常踩…...
手机视频监控客户端APP如何实现跨安卓、苹果和windows平台,并满足不同人的使用习惯
目 录 一、手机视频监控客户端的应用和发展 二、手机视频监控客户端存在的问题 三、HTML5视频监控客户端在手机上实现的方案 (一)HTML5及其优点 (二)HTML5在手机上实现视频应用功能的优势 四、手机HTML5…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...
