Simpy简介:python仿真模拟库-02/5

一、说明
此文为第二部分,若看第一部分。建议查看本系列的第一部分。
二、SymPy — 简化(Simplification)
SymPy 擅长通过其多样化的简化函数来简化数学表达式。在 SymPy 中,您会发现通用的 Simply() 函数,专用于实现表达式最直接的表示。
简化Simplification:simple() 函数位于 sympy.simplify 模块中,旨在使用启发式方法增强输入表达式的简单性。一个例子通过简化表达式 sin²(x) + cos²(x) 来演示其用法。
from sympy import *
x=Symbol('x')
expr=sin(x)**2 + cos(x)**2
simplify(expr)Output:
1三、 展开Expand
Expand() 是 SymPy 中最常见的简化函数之一,用于展开多项式表达式。例如 -
a,b=symbols('a b')
expand((a+b)**2)
expand((a+b)*(a-b))
Expand() 函数通常会增加表达式的大小,尽管它在应用时偶尔会减小表达式的大小。一般来说,调用expand()可能会导致更大的表达式,但也有例外,它会简化它们。
expand((x + 1)*(x - 2) - (x - 1)*x)Output:
-2四、因式分解
该函数接受多项式并将其分解为有理数领域内的不可约分量。
x,y,z=symbols('x y z')
expr=(x**2*z + 4*x*y*z + 4*y**2*z)
factor(expr)
factor(x**2+2*x+1)
Factor() 函数是 Expand() 的逆函数,并保证不可约因子。Factor_list() 提供因子的结构化输出。
expr=(x**2*z + 4*x*y*z + 4*y**2*z)
factor_list(expr)Output:
(1, [(z, 1), (x + 2*y, 2)])五、收集collect
该函数根据表达式列表收集表达式的加法分量,并考虑有理指数幂。
expr=x*y + x - 3 + 2*x**2 - z*x**2 + x**3
expr
六、取消
cancel() 函数的目的是将任何有理函数转换为常规格式 p/q,其中 p 和 q 都是没有共享因子的展开多项式表达式。此外,p 和 q 的前导系数是整数,缺少小数部分。
expr1=x**2+2*x+1
expr2=x+1
cancel(expr1/expr2)Output:
x+1expr = 1/x + (3*x/2 - 2)/(x - 4)
expr
cancel(expr)
七、trigsimp(三角恒等式)
该函数的目的是简化三角恒等式。值得一提的是,反三角函数的命名约定包括在函数名称中添加“a”作为前缀。例如,反余弦表示为“acos()”。
from sympy import trigsimp, sin, cos
from sympy.abc import x, y
expr = 2*sin(x)**2 + 2*cos(x)**2
trigsimp(expr)Output:
2trigsimp 函数使用启发式方法来应用最合适的三角恒等式。
八、指数项简化
该函数通过组合具有相似底数和指数的幂来简化给定的表达式。
expr=x**y*x**z*y**z
expr
powsimp(expr)
您可以通过两种方式控制 powsimp() 的操作方式:仅合并底数或仅合并指数。默认的“全部”模式结合了底数和指数。将“force”设置为 True 会合并基础而不考虑假设。
powsimp(expr, combine='base', force=True)
九、梳子Combsimp
您可以使用 SymPy 的 Combsimp() 函数简化涉及阶乘和二项式的组合表达式。此外,SymPy 还提供了专用的 Factorial() 函数来处理阶乘。
expr=factorial(x)/factorial(x - 3)
expr
为了简化上面的组合表达式,我们使用 Combsimp() 函数,如下所示 -
combsimp(expr)
十、对数组合
该函数采用对数并使用以下规则组合它们 -
- log(x) + log(y) == log(x*y) 如果两者均为正数
- a*log(x) == log(x**a) 如果 x 为正且 a 为实数
logcombine(a*log(x) + log(y) - log(z))
当此功能中启用“force”参数时,除非对数量存在现有假设,否则它将假设上述条件有效。
logcombine(a*log(x) + log(y) - log(z), force=True)
十一、SymPy — 导数
函数的导数表示其变量之一的变化速度。这对应于确定特定点处切线的斜率。在 SymPy 中,您可以使用“diff()”函数计算带有变量的数学表达式的微分。
diff(expr, variable)
from sympy import diff, sin, exp
from sympy.abc import x,y
expr=x*sin(x*x)+1 >>> expr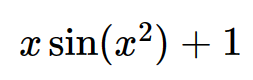
diff(expr,x)
diff(exp(x**2),x)
要计算多重导数,只需重复每个微分步骤的变量或通过在变量后指定数值来指示所需的顺序。
diff(x**4,x,3)Output:
24xfor i in range(1,4): print (diff(x**4,x,i))Output:
4*x**3
12*x**2
24*x也可以调用表达式的 diff() 方法。它的工作原理与 diff() 函数类似。
expr=x*sin(x*x)+1
expr.diff(x)
SymPy 中的 Derivative 类允许您创建未计算的导数,与 diff() 函数共享相同的语法。要获得该导数的实际结果,您可以应用 doit 方法。
from sympy import Derivative
d=Derivative(expr)
d
d.doit()
十二、SymPy — 集成
在 SymPy 包中,您将找到积分模块,该模块设计用于计算数学表达式的定积分和不定积分。当在表达式后面提供变量时,integrate() 方法可以计算原始积分或不定积分。
integrate(f, x)要计算定积分,请按如下方式传递参数 -
(integration_variable, lower_limit, upper_limit)from sympy import *
x,y = symbols('x y')
expr=x**2 + x + 1
integrate(expr, x)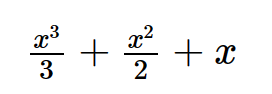
expr=sin(x)*tan(x)
expr
integrate(expr,x)
expr=exp(-x**2)
integrate(expr,(x,0,oo) )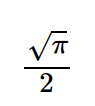
您可以使用 Integral 对象创建未计算的积分,该对象可以通过调用 doit() 方法进行计算。
expr = Integral(log(x)**2, x)
expr
expr.doit()![]()
十三、积分变换
SymPy 支持各种类型的积分变换,如下所示 -
- 拉普拉斯变换
- 傅里叶变换
- 正弦变换
- 余弦变换
- 汉克尔变换
提到的函数位于 sympy.integrals.transforms 模块内。提供的示例说明了傅立叶变换和拉普拉斯变换的计算。
实施例1
from sympy import fourier_transform, exp
from sympy.abc import x, k
expr=exp(-x**2)
fourier_transform(expr, x, k)在 python shell 中执行上述命令时,将生成以下输出 -
sqrt(pi)*exp(-pi**2*k**2)这相当于 -

实施例2
from sympy.integrals import laplace_transform
from sympy.abc import t, s, a
laplace_transform(t**a, t, s)在 python shell 中执行上述命令时,将生成以下输出 -
(s**(-a)*gamma(a + 1)/s, 0, re(a) > -1)十四、SymPy — 矩阵
在数学领域,矩阵是元素的结构化排列,可以包含数字、符号或数学表达式。矩阵运算的概念涉及对这些矩阵结构执行各种数学运算,所有这些运算都遵循特定的数学准则。
矩阵的一个值得注意的应用在于线性变换领域,这是许多科学学科中的一个重要概念,特别是在基于矩阵的方法学广泛应用的物理领域。
在 SymPy 包中,有一个用于处理矩阵的专用模块。该模块介绍了 Matrix 类,它是一个基本组件,可用作矩阵的表示并促进矩阵的操作。
from sympy.matrices import Matrixfrom sympy.matrices import Matrix
m=Matrix([[1,2,3],[2,3,1]])
m
矩阵是从适当大小的列表对象创建的。您还可以通过将列表项分布在指定数量的行和列中来获取矩阵。
M=Matrix(2,3,[10,40,30,2,6,9])
M
矩阵是一个可变对象。矩阵模块还提供了 ImmutableMatrix 类来获取不可变矩阵。
十五、基本操控
Matrix 对象的shape属性返回其大小。
M.shapeOutput:
(2,3)row() 和 col() 方法分别返回指定数量的行或列。
M.row(0)Output:
[10 40 30]M.col(1)
使用 Python 的切片运算符来获取属于行或列的一项或多项。
M.row(1)[1:3]Output:
[6, 9]Matrix 类具有 row_del() 和 col_del() 方法,可从给定矩阵中删除指定的行/列 -
M=Matrix(2,3,[10,40,30,2,6,9])
M.col_del(1)
M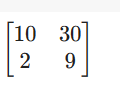
您可以使用以下命令将样式应用于输出 -
M.row_del(0)
MOutput:
[2 6 9]类似地,row_insert() 和 col_insert() 方法在指定的行或列索引处添加行或列
M1=Matrix([[10,30]])
M=M.row_insert(0,M1)
M
十六、算术运算
定义常用运算符 +、— 和 * 来执行加法、减法和乘法。
M1=Matrix([[1,2,3],[3,2,1]])
M2=Matrix([[4,5,6],[6,5,4]])
M1+M2
M1-M2
矩阵乘法可以在第一个矩阵中的列数与第二个矩阵中的行数匹配的条件下发生。此外,结果将具有与第一个矩阵相同的行数和与第二个矩阵相同的列数。
M1=Matrix([[1,2,3],[3,2,1]])
M2=Matrix([[4,5],[6,6],[5,4]])
M1*M2
十七、矩阵构造函数
SymPy 提供各种专门的矩阵类,例如单位矩阵和全零或全填充的矩阵。这些类分别用名称“eye”、“zeros”和“ones”表示。具体来说,单位矩阵是一个方阵,其中沿对角线的所有元素都等于 1,而所有其他元素都设置为 0。
from sympy.matrices import eye
eye(3)
在对角矩阵中,对角线上的元素根据提供的参数进行初始化。
from sympy.matrices import diag
diag(1,2,3)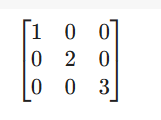
零矩阵中的所有元素都初始化为 0。
from sympy.matrices import zeros
zeros(2,3)
同样,ones 是所有元素都设置为 1 的矩阵。
from sympy.matrices import ones
ones(2,3)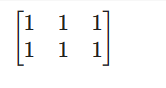
到目前为止,一切都很好。我们已经看到使用该库的各种简化,数学工具箱绝对是好的。在接下来的部分中,我们将了解如何定义和使用本质上构成模拟构建块的函数。
相关文章:
Simpy简介:python仿真模拟库-02/5
一、说明 关于python下的仿真库,本篇为第二部分,是更进一步的物理模型讲解,由于这部分内容强依赖于第一部分的符号介绍,因此,有以下建议: 此文为第二部分,若看第一部分。建议查看本系列的第一部…...

Kafka高级应用:如何配置处理MQ百万级消息队列?
在大数据时代,Apache Kafka作为一款高性能的分布式消息队列系统,广泛应用于处理大规模数据流。本文将深入探讨在Kafka环境中处理百万级消息队列的高级应用技巧。 本文,已收录于,我的技术网站 ddkk.com,有大厂完整面经…...

LIN总线学习笔记(1)-总线传输规范
关注菲益科公众号—>对话窗口发送 “CANoe ”或“INCA”,即可获得canoe入门到精通电子书和INCA软件安装包(不带授权码)下载地址。 接触LIN是从最近负责项目中开始的。项目已经快要量产了,因为中间遇到的大大小小的问题…...

Qt界面篇:Qt停靠控件QDockWidget、树控件QTreeWidget及属性控件QtTreePropertyBrowser的使用
1、功能介绍 本篇主要使用Qt停靠控件QDockWidget、树控件QTreeWidget及Qt属性控件QtTreePropertyBrowser来搭建一个简单实用的主界面布局。效果如下所示。 2、控件使用详解 2.1 停靠控件QDockWidget QDockWidget可以停靠在 QMainWindow 内或作为桌面上的顶级窗口浮动。默认值…...
H266/VVC网络适配层概述
视频编码标准的分层结构 视频数据分层的必要性:网络类型的多样性、不同的应用场景对视频有不同的需求。 编码标准的分层结构:为了适应不同网络和应用需求,视频编码数据根据其内容特性被分成若干NAL单元(NAL Unit,NALU…...
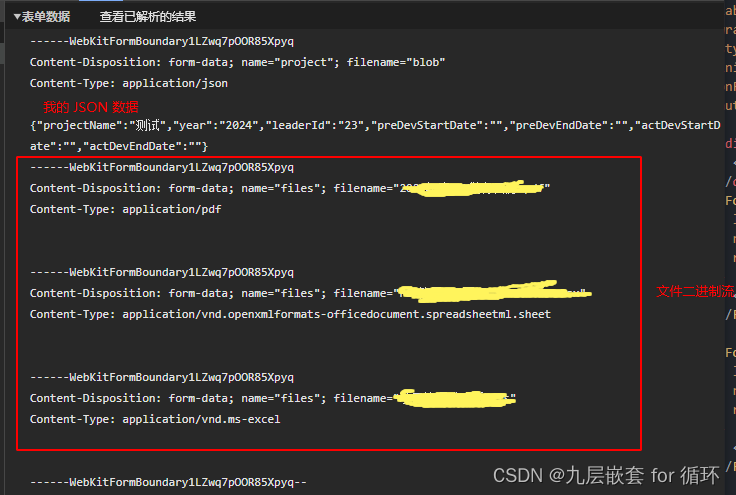
new FormData 同时发送表单 json 以及文件二进制流
需要新增时同时发送表单 json 以及对应的文件即可使用以下方法传参 let formDataParams new FormData(); 首先通过 new FormData() 创建你需要最后发送的表单 接着将你的对象 json 存储,注意使用 new Blob 创建大表单转换成 json 格式。以…...
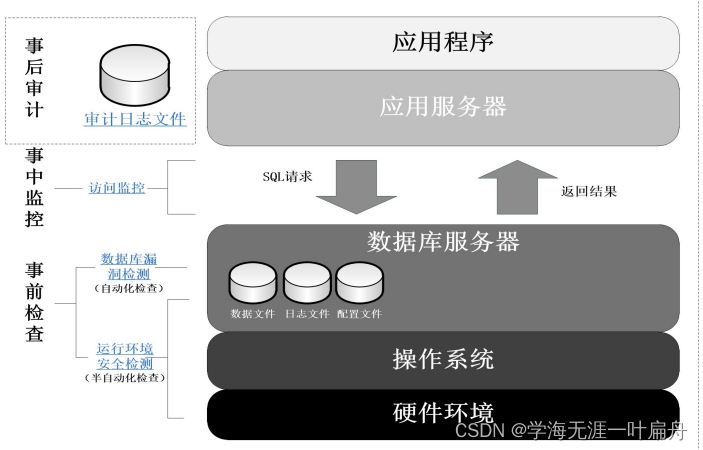
计算机环境安全
操作系统安全----比如windows,linux 安全标识--实体唯一性 windows---主体:账户,计算机,服务 安全标识符SID-Security Identifier 普通用户SID是1000,管理用SID是500 linux---主体:用户,用户组…...

Activiti7工作流引擎:多租户
一:多租户 表示每个租户之间数据隔离互不影响,互不可见。通常一个租户表示一个系统应用(类似于appid的作用)或者一家公司。 通过数据库级别进行隔离,每个租户对应一个数据库;通过表记录级别进行隔离&…...
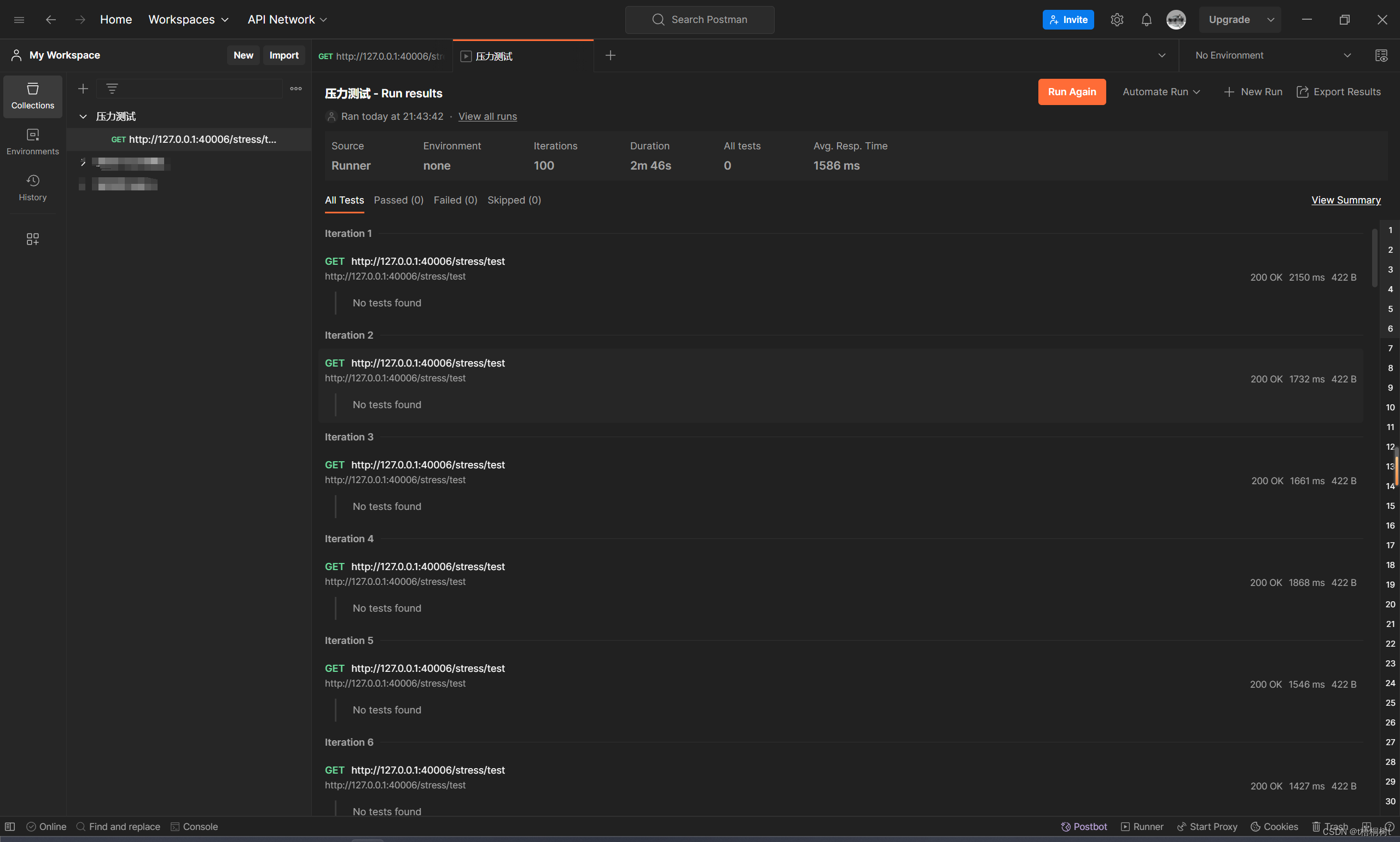
Postman实现压力测试
从事软件开发对于压力测试并不陌生,常见的一些压测软件有Apache JMeter LoadRunner Gatling Tsung 等,这些都是一些比较专业的测试软件,对于我的工作来说一般情况下用不到这么专业的测试,有时候需要对一些接口进行压力测试又不想再安装新软件,那么可以使用Postman来实现对…...
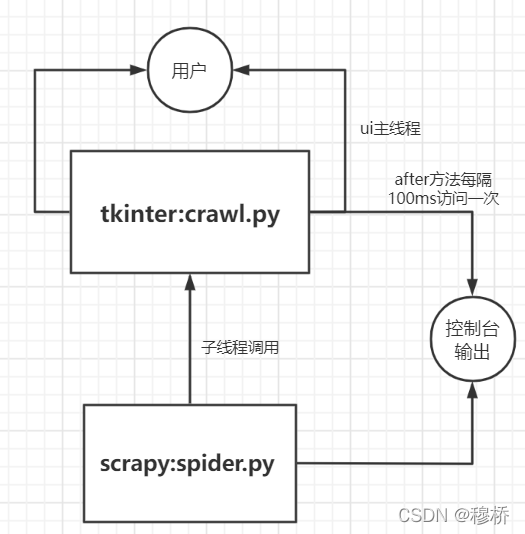
爬虫工具(tkinter+scrapy+pyinstaller)
需求介绍输入:关键字文件,每一行数据为一爬取单元。若一行存在多个and关系的关键字 ,则用|隔开处理:爬取访问6个网站的推送,获取推送内容的标题,发布时间,来源,正文第一段࿰…...

MySQL常用sql语句记录
1,创建用户及赋权 -- 创建用户 CREATE USER usernamelocalhost IDENTIFIED BY password;-- 赋予所有权限 GRANT ALL PRIVILEGES ON database_name.* TO usernamelocalhost;-- 赋予特定表的某些权限 GRANT SELECT, INSERT ON table_name TO usernamelocalhost;-- 更…...

2024.1.4力扣每日一题——被列覆盖的最多行数
2024.1.4 题目来源我的题解方法一 回溯位运算优化 题目来源 力扣每日一题;题序:2397 我的题解 方法一 回溯位运算优化 这道题一看就会想到使用回溯法,但是采用回溯法后如何判断有多少行被覆盖,直接计算矩阵时间复杂度较高&…...
Elasticsearch:Serarch tutorial - 使用 Python 进行搜索 (一)
本实践教程将教你如何使用 Elasticsearch 构建完整的搜索解决方案。 在本教程中你将学习: 如何对数据集执行全文关键字搜索(可选使用过滤器)如何使用机器学习模型生成、存储和搜索密集向量嵌入如何使用 ELSER 模型生成和搜索稀疏向量如何使用…...

第五讲_css元素显示模式
css元素显示模式 1. 元素的显示模式1.1 块元素1.2 行内元素1.3 行内块元素 2. 元素根据显示模式分类3. 修改元素的显示模式 1. 元素的显示模式 1.1 块元素 块元素的特性: 在页面中独占一行,从上到下排列。默认宽度,撑满父元素。默认高度&a…...

Shell脚本入门实战:探索自动化任务与实用场景
引言 Shell脚本作为一种强大的自动化工具,在现代操作系统中具有广泛的应用。无论是简单的文件操作,还是复杂的系统管理,Shell脚本都能提供高效、快速的解决方案。在本文中,我们将探索Shell脚本的基础知识,并通过实战场…...

【AI视野·今日Sound 声学论文速览 第四十二期】Fri, 5 Jan 2024
AI视野今日CS.Sound 声学论文速览 Fri, 5 Jan 2024 Totally 10 papers 👉上期速览✈更多精彩请移步主页 Daily Sound Papers PosCUDA: Position based Convolution for Unlearnable Audio Datasets Authors Vignesh Gokul, Shlomo Dubnov深度学习模型需要大量干净的…...

Java中如何使用SQLite数据库
目录 SQLite简介SQLite优势安装 SQLite基本使用Java使用SQLite Springboot使用SQLite1.添加依赖2.配置数据库3.创建实体类 4.创建Repository接口5.创建控制器6.运行应用程序 SQLite简介 SQLite 是一个开源的嵌入式关系数据库,实现了自给自足的、无服务器的、配置无…...

kettle的基本介绍和使用
1、 kettle概述 1.1 什么是kettle Kettle是一款开源的ETL工具,纯java编写,可以在Window、Linux、Unix上运行,绿色无需安装,数据抽取高效稳定。 1.2 Kettle核心知识点 1.2.1 Kettle工程存储方式 以XML形式存储以资源库方式存储…...

数据结构第2章 栈和队列
名人说:莫听穿林打叶声,何妨吟啸且徐行。—— 苏轼《定风波莫听穿林打叶声》 本篇笔记整理:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 目录 0、思维导图栈和队列1、栈1)特点2࿰…...

Axure鲜花商城网站原型图,网上花店订花O2O本地生活电商平台
作品概况 页面数量:共 30 页 兼容软件:仅支持Axure RP 9/10,非程序软件无源代码 应用领域:鲜花网、花店网站、本地生活电商 作品特色 本作品为「鲜花购物商城」网站模板,高保真高交互,属于O2O本地生活电…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...
