每日算法打卡:数的三次方根 day 7
文章目录
- 原题链接
- 题目描述
- 输入格式
- 输出格式
- 数据范围
- 输入样例:
- 输出样例:
- 题目分析
- 示例代码
原题链接
790. 数的三次方根
题目难度:简单
题目描述
给定一个浮点数 n,求它的三次方根。
输入格式
共一行,包含一个浮点数 n。
输出格式
共一行,包含一个浮点数,表示问题的解。
注意,结果保留 6 位小数。
数据范围
−10000≤n≤10000
输入样例:
1000.00
输出样例:
10.000000
题目分析
这道题就很简单了,就是给我们一个数求他的三次方根,首先三次方根的函数图像如下
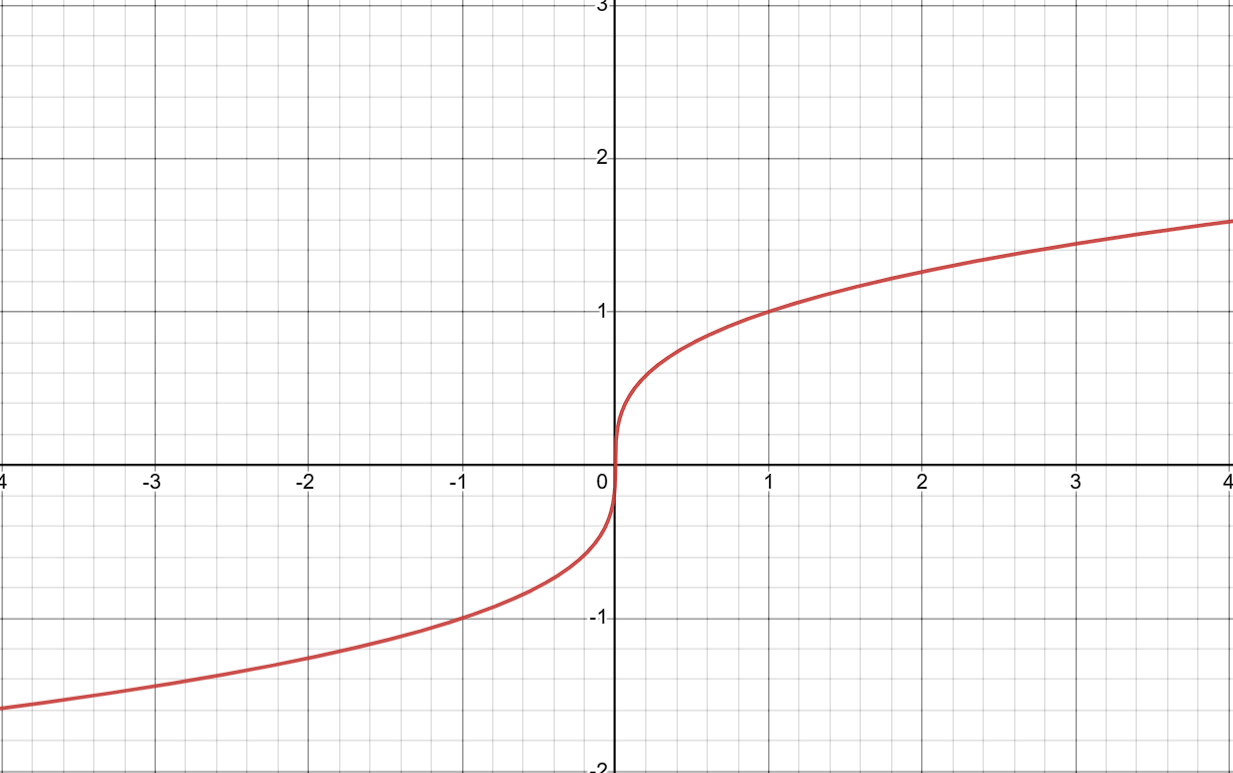
他的图像是具有单调性的,因此可以使用二分法进行逼近
我们确定一个区间范围,最大的范围就是在负一万到正一万之间,之后逐渐缩小
对于这个判断条件,其实可以选择小于等于目标值也可以取大于等于目标值,我们只需要每次取中点,自乘三次,与输入值比较即可,如果大于等于,说明M取大了,要将右端点缩小,如果小于等于,说明M取小了,将左端点向右移动即可
补充,这里对于浮点数的等于比较,受限于精度,我们只要求他的差值小于某一个极小的数,则认为他们两个数相等
示例代码
#include<iostream>
#include<cmath>
#include<cstdio>
using namespace std;
int main()
{double x;cin >> x;double l = -1e4;double r = 1e4;while (fabs(r - l) > 1e-7) // 绝对值小于10的负7次方{double mid = (l + r) / 2;if (mid * mid * mid >= x) r = mid;else l = mid;}printf("%.6f",l); // 控制精度输出return 0;
}
相关文章:

每日算法打卡:数的三次方根 day 7
文章目录 原题链接题目描述输入格式输出格式数据范围输入样例:输出样例: 题目分析示例代码 原题链接 790. 数的三次方根 题目难度:简单 题目描述 给定一个浮点数 n,求它的三次方根。 输入格式 共一行,包含一个浮…...
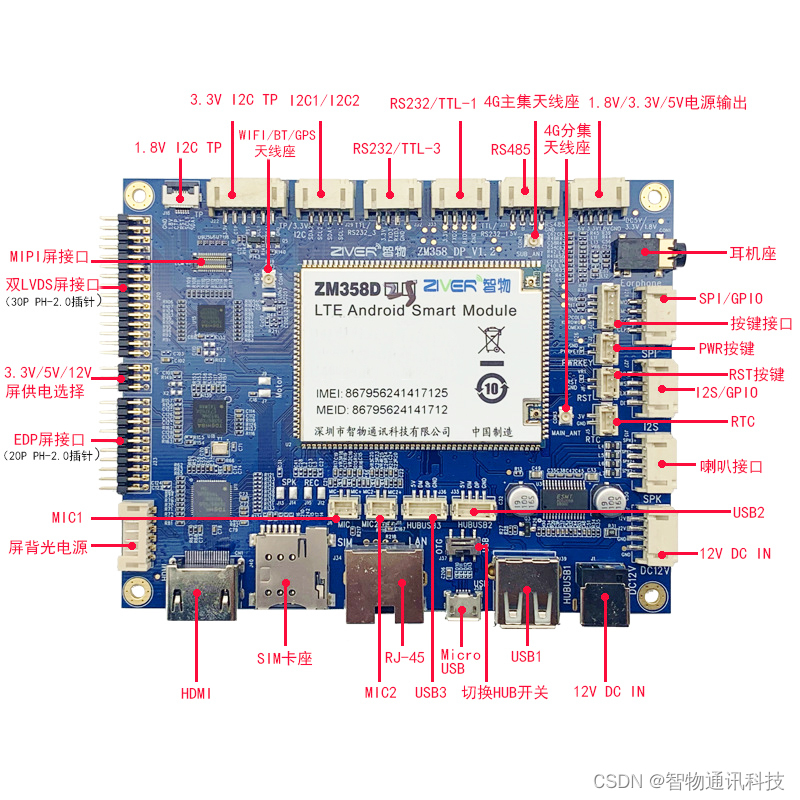
人机交互主板定制_基于MT8735安卓核心板的自助查询机方案
人机交互主板是一种商显智能终端主板,广泛应用于广告机、工控一体机、教学一体机、智能自助终端、考勤机、智能零售终端、O2O智能设备、取号机、计算机视觉、医疗健康设备、机器人设备等领域。 人机交互主板采用联发科MTK8735芯片平台,四核Cortex-A53架构…...

全志F1C100s Linux 系统编译出错:不能连接 github
环境 Ubuntu 20.04 LTS 64 位虚拟机 开发板:Lichee Pi Nano 源代码:GitHub - florpor/licheepi-nano 问题描述 该源码库使用了 git 子模块的概念,一个库中包含了 u-boot、Linux等代码库。不需要分别编译,一个 make 全搞定 编译时提示错误: >>> linux-hea…...

如何保障 MySQL 和 Redis 的数据一致性?
数据一致性问题是如何产生的? 数据一致性问题通常产生于数据在不同的时间点、地点或系统中存在多个副本的情况, 系统只存在一个副本的情况下也完全可能会产生。 设想一下,你在一家连锁咖啡店有一张会员卡这张会员卡可以绑定两个账号&#x…...

Leetcode 2999. Count the Number of Powerful Integers
Leetcode 2999. Count the Number of Powerful Integers 1. 解题思路2. 代码实现 题目链接:10034. Count the Number of Powerful Integers 1. 解题思路 这一题的话其实还是一个典型的求不大于 N N N的特殊数字个数的问题。 这道题本质上进行一下替换还是要求如…...

【Reading Notes】(2)
文章目录 FreestyleHip-hop dance and MusicProgrammerMaster Freestyle 都说人的成长有三个阶段,第一个阶段认为自己独一无二,天之骄子;第二个阶段发现自己原来如此渺小,如此普通,沮丧失望;第三阶段&#…...

【设计模式之美】SOLID 原则之一:怎么才算是单一原则、如何取舍单一原则
文章目录 一. 如何判断类的职责是否足够单一?二. 类的职责是否设计得越单一越好? 开始学习一些经典的设计原则,其中包括,SOLID、KISS、YAGNI、DRY、LOD 等。 本文主要学习单一职责原则的相关内容。 单一职责原则的定义:…...

# [NOIP2015 普及组] 扫雷游戏#洛谷
题目背景 NOIP2015 普及组 T2 题目描述 扫雷游戏是一款十分经典的单机小游戏。在 n n n 行 m m m 列的雷区中有一些格子含有地雷(称之为地雷格),其他格子不含地雷(称之为非地雷格)。玩家翻开一个非地雷格时&#…...

Unity中Shader的_Time精度问题
文章目录 前言一、U方向上优化二、V方向上优化在这里插入图片描述 三、最终代码1、效果2、Shader 前言 在Unity的Shader中,使用了_Time来达到UV的流动效果,普遍会出现一个问题。我们的UV值会随着时间一直增加(uv值增加了,但是因为…...

听GPT 讲Rust源代码--compiler(15)
File: rust/compiler/rustc_arena/src/lib.rs 在Rust源代码中,rustc_arena/src/lib.rs文件定义了TypedArena,ArenaChunk,DroplessArena和Arena结构体,以及一些与内存分配和容器操作相关的函数。 cold_path<F: FnOnce,drop,new,…...

关键字联合体union的定义和使用
联合体的定义 联合体的定义和结构体相同。 联合体成员共用存储空间,联合体占用的空间最大长度的数据成员的长度。 union State {char sleep;char run;int suspend;double error; }state_u;以上例子,State表示联合体的名字,它相当于声明了一…...

基于GA-PSO遗传粒子群混合优化算法的VRPTW问题求解matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.本算法原理 4.1 遗传算法(GA)基本原理 4.2 粒子群优化(PSO)基本原理 4.3 算法优化策略 5.完整程序 1.程序功能描述 VRPTW是车辆路径问题(VR…...

【leetcode100-033】【链表】排序链表
【题干】 给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。 【思路】 递归版归并法链表版~没什么特别好说的(非递归版归并也是可以哒,但是马上要考试了今天懒得写了!打个flag在这里也许哪天想起来…...
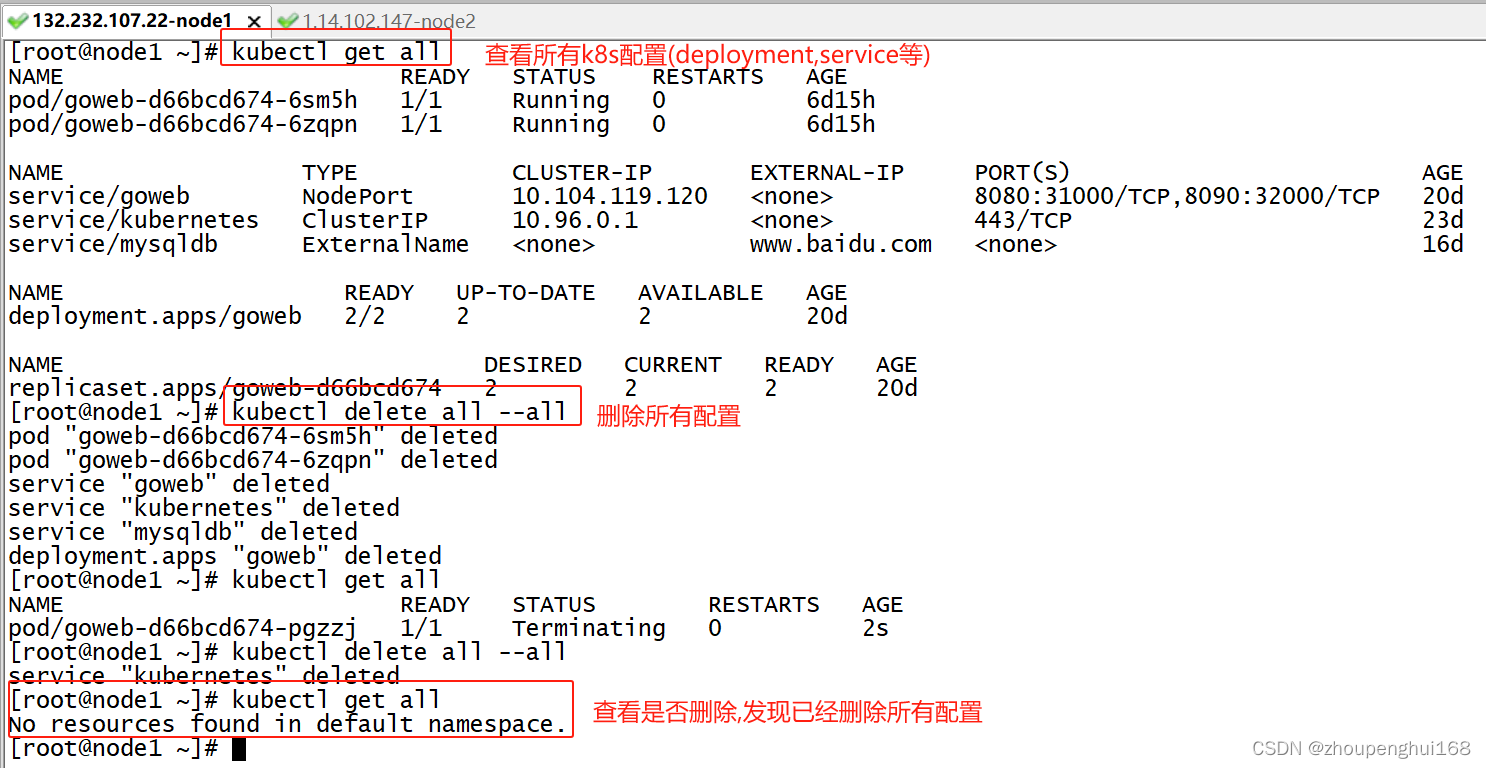
[Kubernetes]5. k8s集群StatefulSet详解,以及数据持久化(SC PV PVC)
前面通过deployment结合service来部署无状态的应用,下面来讲解通过satefulSet结合service来部署有状态的应用 一.StatefulSet详解 1.有状态和无状态区别 无状态: 无状态(stateless)、牲畜(cattle)、无名(nameless)、可丢弃(disposable) 有状态: 有状态(stateful)、宠物(pet)…...

数据库系统-甘晴void学习笔记
数据库系统笔记 计科210X 甘晴void 202108010XXX 教材:《数据库系统概论》第6版 (图片来源于网络,侵删) 文章目录 数据库系统<br>笔记第一篇 基础篇1 绪论1.1数据库系统概述1.2数据模型1.3数据库系统的结构(三级模式结构…...

Azure Machine Learning - 人脸识别任务概述与技术实战
Azure AI 人脸服务提供了可检测、识别和分析图像中的人脸的 AI 算法。 人脸识别软件在许多不同情形中都十分重要,例如识别、无接触访问控制和实现隐私的人脸模糊。你可以通过客户端库 SDK,或者直接调用 REST API 使用人脸服务。 目录 一、人脸识别服务场…...
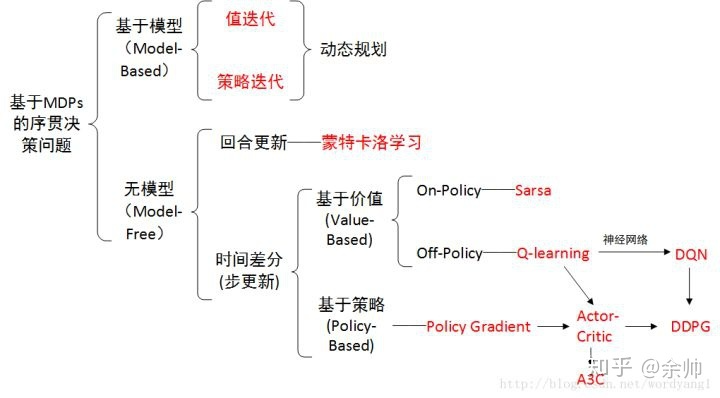
强化学习的数学原理学习笔记 - 蒙特卡洛方法(Monte Carlo)
文章目录 概览:RL方法分类蒙特卡洛方法(Monte Carlo,MC)MC BasicMC Exploring Starts🟦MC ε-Greedy 本系列文章介绍强化学习基础知识与经典算法原理,大部分内容来自西湖大学赵世钰老师的强化学习的数学原理…...
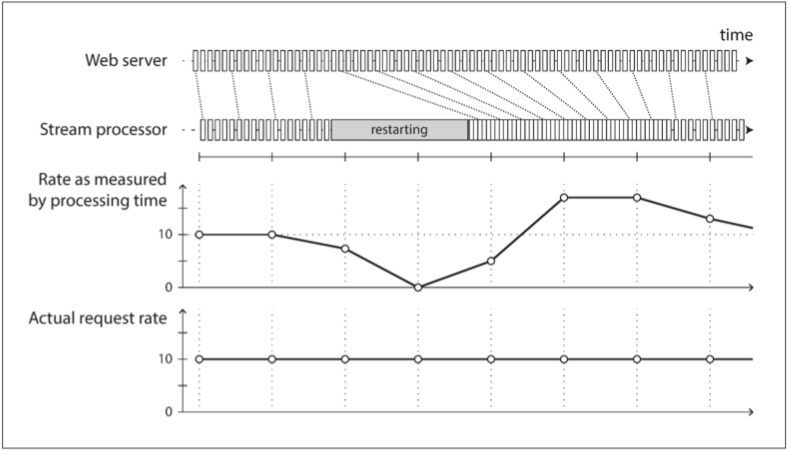
DDIA 第十一章:流处理
本文是《数据密集型应用系统设计》(DDIA)的读书笔记,一共十二章,我已经全部阅读并且整理完毕。 采用一问一答的形式,并且用列表形式整理了原文。 笔记的内容大概是原文的 1/5 ~ 1/3,所以你如果没有很多时间…...

webpack知识点总结(高级应用篇)
除开公共基础配置之外,我们意识到两点: 1. 开发环境(modedevelopment),追求强大的开发功能和效率,配置各种方便开 发的功能;2. 生产环境(modeproduction),追求更小更轻量的bundle(即打包产物); 而所谓高级应用,实际上就是进行 Webpack 优化…...

均匀与准均匀 B样条算法
B 样条曲线的定义 p ( t ) ∑ i 0 n P i F i , k ( t ) p(t) \sum_{i0}{n} P_i F_{i, k}(t) p(t)i0∑nPiFi,k(t) 方程中 n 1 n1 n1 个控制点, P i P_i Pi, i 0 , 1 , ⋯ n i0, 1, \cdots n i0,1,⋯n 要用到 n 1 n1 n1 个 k k k 次 B 样条基函数 …...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
