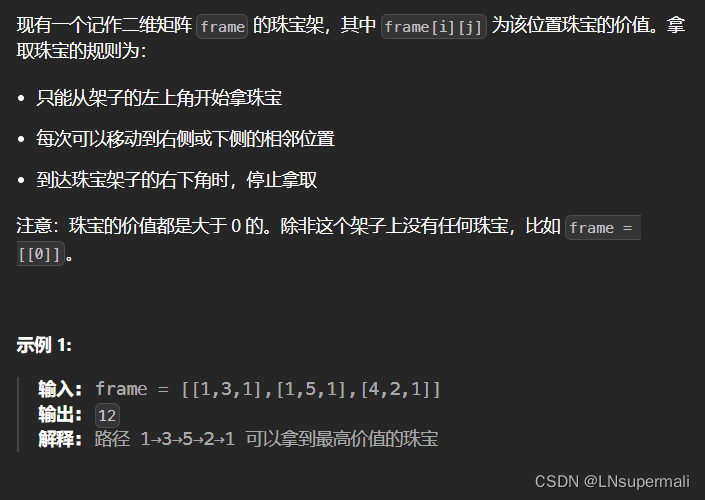
力扣LCR 166. 珠宝的最高价值(java 动态规划)
Problem: LCR 166. 珠宝的最高价值
文章目录
- 解题思路
- 思路
- 解题方法
- 复杂度
- Code
解题思路
思路
改题目与本站64题实质上是一样的,该题目在64题的基础上将求取最小路径和改成了求取最大路径和。具体实现思路如下:
1.定义一个int类型的二维数组dp大小为给定矩阵frame的行数与列数。该数组用于记录每个当前阶段的最大路径和(也是本题目的最大价值)
2.动态转移方程为**dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + frame[i][j];**即当前位置(也可以记作阶段)最大值每次取出其上方,和左侧的较大值的一个与当前frame位置值作和;
3.由于dp数组中第一行与第一列无法直接执行动态转移方程,要对其初始化:第一行每个位置值为依次向右累加;第一列每个位置值为依次向下累加
3.最后返回dp数组中的最后一个值即可。
解题方法
1.定义数组frame的行数rows与列数columns;并定义一个int变量temp用于记录累加和
2.定义并初始化int类型数组dp初始化为new int[rows][colunms]
3.初始化dp的第一行与第一列,在for循环中使temp依次累加当前第一行(列)位置的值,并赋值给当前dp数组位置;
4.从dp数组的第二行(索引为1)开始执行动态转移方程dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + frame[i][j];,最后返回dp[rows - 1][columns - 1];
复杂度
时间复杂度:
O ( M N ) O(MN) O(MN),其中 M M M为数组frame的行数, N N N为其列数
空间复杂度:
O ( M N ) O(MN) O(MN)
Code
class Solution {/*** The maximum path sum is obtained using dynamic programming** @param frame Given matrix* @return int*/public int jewelleryValue(int[][] frame) {int rows = frame.length;int columns = frame[0].length;int temp = 0;//Records the current maximum path sumint[][] dp = new int[rows][columns];//Handle the first row and columnfor (int i = 0; i < columns; ++i) {temp += frame[0][i];dp[0][i] = temp;}temp = 0;for (int j = 0; j < rows; ++j) {temp += frame[j][0];dp[j][0] = temp;}//Dynamic transfer equationfor (int i = 1; i < rows; ++i) {for (int j = 1; j < columns; ++j) {dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + frame[i][j];}}return dp[rows - 1][columns - 1];}
}
相关文章:
力扣LCR 166. 珠宝的最高价值(java 动态规划)
Problem: LCR 166. 珠宝的最高价值 文章目录 解题思路思路解题方法复杂度Code 解题思路 思路 改题目与本站64题实质上是一样的,该题目在64题的基础上将求取最小路径和改成了求取最大路径和。具体实现思路如下: 1.定义一个int类型的二维数组dp大小为给定…...
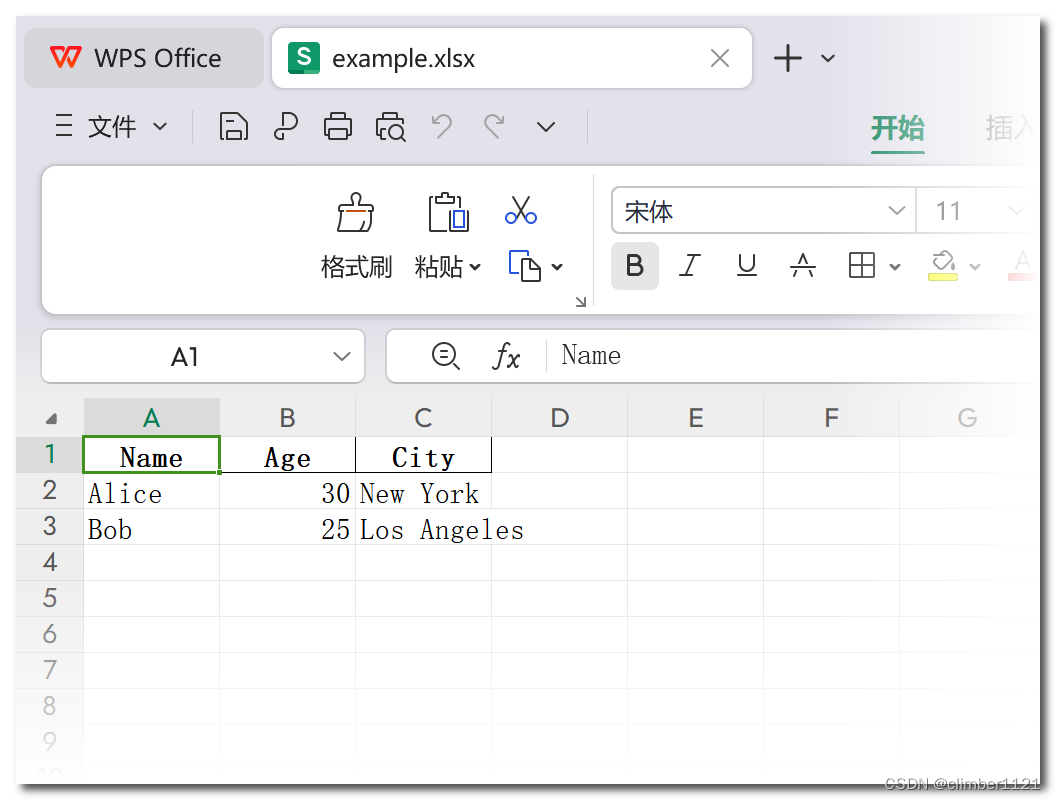
【Python基础】一文搞懂:Python 中 Excel 文件的写入与读取
文章目录 1 引言2 使用 openpyxl2.1 安装 openpyxl2.2 写入 Excel 文件2.3 读取 Excel 文件 3 使用 pandas3.1 安装 pandas 和 openpyxl3.2 写入 Excel 文件3.3 读取 Excel 文件 4 实例演示4.1 安装所需库4.2 封装为excel_example.py脚本文件 5 注意事项6 总结 1 引言 在现代办…...

二叉树题目:完全二叉树插入器
文章目录 题目标题和出处难度题目描述要求示例数据范围 解法思路和算法代码复杂度分析 题目 标题和出处 标题:完全二叉树插入器 出处:919. 完全二叉树插入器 难度 6 级 题目描述 要求 完全二叉树是每一层(除最后一层外)都…...
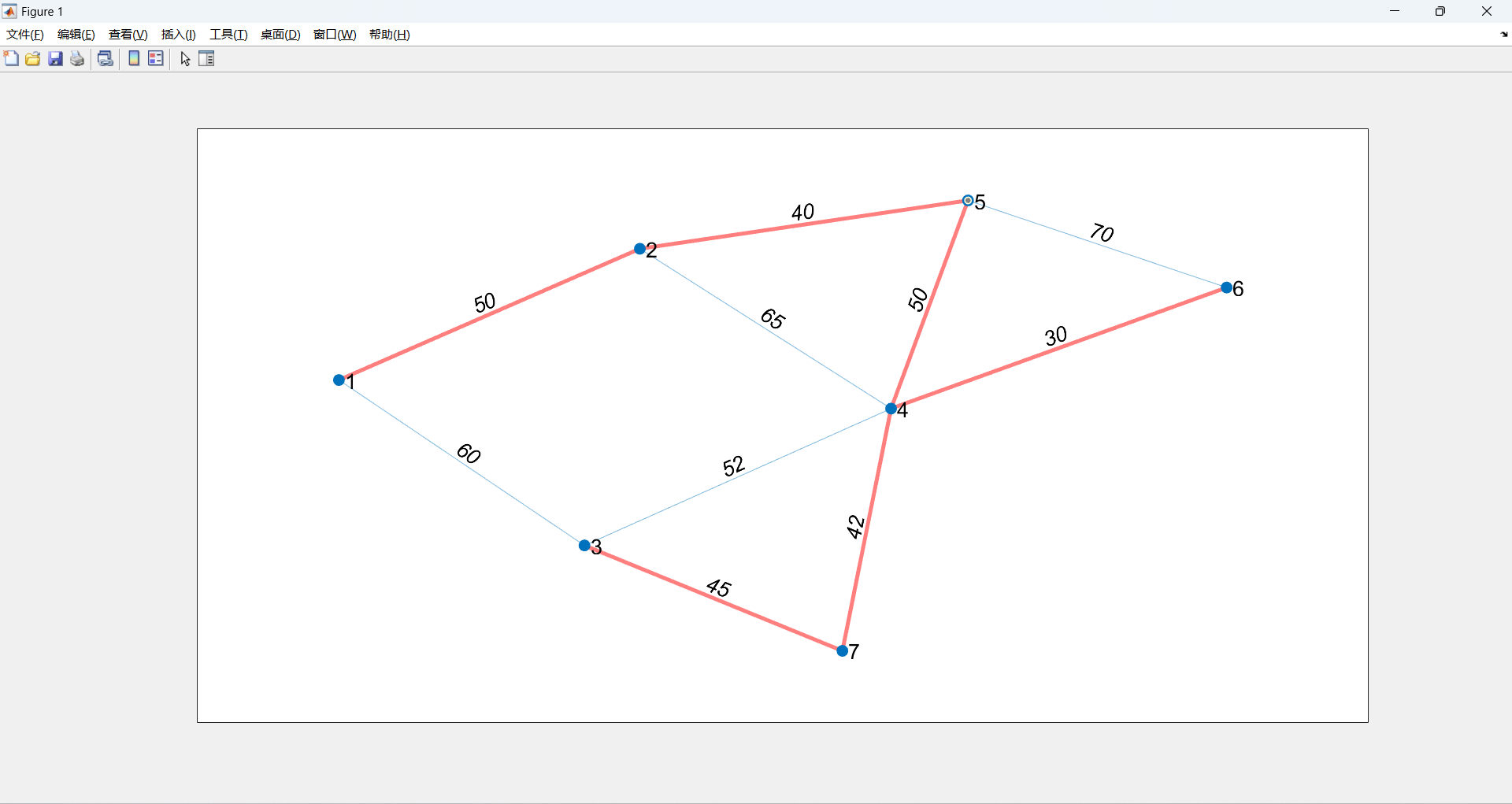
用MATLAB求最短路径(graphshortestpath)和求最小生成树(minspantree),代码演示
求最短路径(graphshortestpath),求最小生成树(minspantree) 文章目录 求最短路径(graphshortestpath),求最小生成树(minspantree)1、最短路径问题2、最小生成…...
用win系统搭建Minecraft世界服务器,MC开服教程,小白开服教程
雨云VPS用Windows系统搭建我的世界世界服务器,Minecraft开服教程,小白开服教程,MC 1.19.4版本服务器搭建教程。 此教程使用 Mohist 1.19.4 服务端,此服务端支持Forge模组和Bukkit/Spigot/Paper插件,如果需要开其他服务…...
MacOS安装Miniforge、Tensorflow、Jupyter Lab等(2024年最新)
大家好,我是邵奈一,一个不务正业的程序猿、正儿八经的斜杠青年。 1、世人称我为:被代码耽误的诗人、没天赋的书法家、五音不全的歌手、专业跑龙套演员、不合格的运动员… 2、这几年,我整理了很多IT技术相关的教程给大家࿰…...
iOS 应用上架指南:资料填写及提交审核
摘要 本文提供了iOS新站上架资料填写及提交审核的详细指南,包括创建应用、资料填写-综合、资料填写-IOS App和提交审核等步骤。通过本指南,您将了解到如何填写正确的资料,并顺利通过苹果公司的审核。 引言 在开发iOS应用后,将其…...
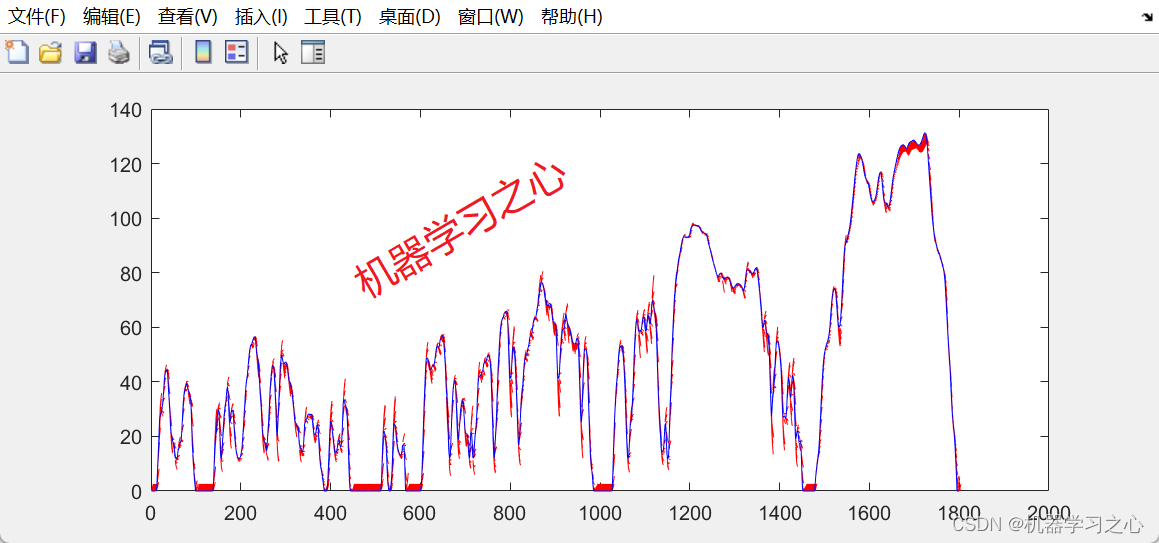
车速预测 | Matlab基于RBF径向基神经网络的车速预测模型(多步预测,尾巴图)
目录 效果一览基本介绍程序设计参考资料 效果一览 基本介绍 车速预测 | Matlab基于RBF径向基神经网络的车速预测模型(多步预测,尾巴图) 程序设计 完整程序和数据获取方式:私信博主回复Matlab基于RBF径向基神经网络的车速预测模型…...
MySQL 5.7.35下载安装使用_忘记密码_远程授权
文章目录 MySQL 5.7.35下载安装使用_忘记密码_远程授权MySQL下载地址mysql安装点击安装,最好以管理员身份运行选择自定义安装选择64位勾选启动自定义产品执行点击同意点击下一步点击执行下一步配置数据库端口号设置登录密码,如果密码忘记,下面…...

openGauss学习笔记-194 openGauss 数据库运维-常见故障定位案例-分析查询语句长时间运行的问题
文章目录 openGauss学习笔记-194 openGauss 数据库运维-常见故障定位案例-分析查询语句长时间运行的问题194.1 分析查询语句长时间运行的问题194.1.1 问题现象194.1.2 原因分析194.1.3 处理办法 openGauss学习笔记-194 openGauss 数据库运维-常见故障定位案例-分析查询语句长时…...

GoLang:gRPC协议的介绍以及详细教程,从Protocol开始
目录 编辑 引言 一、安装相关Go语言库和相关工具 1. 安装Go 2. 安装Protocol Buffers Compiler 2.1 Windows 2.1.1 下载 2.1.2 解压 2.1.3 环境变量 2. macOS 3. Linux 4. 验证安装 3. 安装gRPC-Go 4. 安装Protocol Buffers的Go插件 二、定义服务 三、生成Go…...

LeetCode-2645. 构造有效字符串的最少插入数
给你一个字符串 word ,你可以向其中任何位置插入 “a”、“b” 或 “c” 任意次,返回使 word 有效需要插入的最少字母数。 如果字符串可以由 “abc” 串联多次得到,则认为该字符串有效 。 示例 1: 输入:word “b” …...
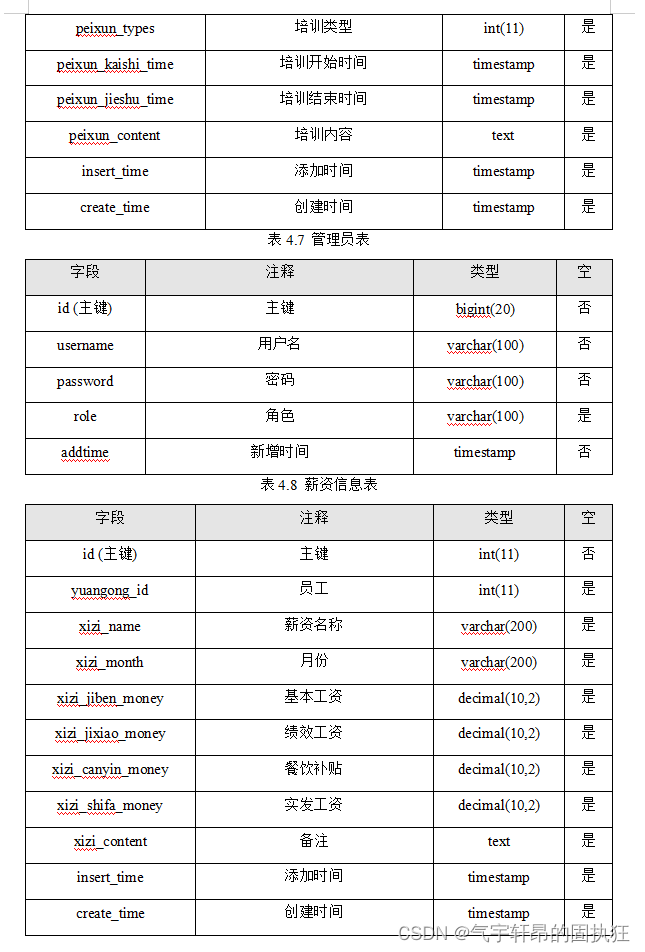
ssm+vue的城投公司企业人事管理系统设计与实现(有报告)。Javaee项目,ssm vue前后端分离项目。
演示视频: ssmvue的城投公司企业人事管理系统设计与实现(有报告)。Javaee项目,ssm vue前后端分离项目。 项目介绍: 采用M(model)V(view)C(controller&#x…...

nginx基础面试题以及配置文件解析和命令控制
目录 1、nginx是什么 2、nginx的特点 3、为什么中国大陆有:百度、京东、新浪、网易、腾讯、淘宝等这么多用户使用nginx 4、nginx 的内部技术架构 上一期我们配置安装了nginx接着讲一下nginx配置文件的解析和nginx 命令控制 感谢观看!希望能够帮助到…...
全自动网页生成系统网站源码重构版
源码优点: 所有模板经过精心审核与修改,完美兼容小屏手机大屏手机,以及各种平板端、电脑端和360浏览器、谷歌浏览器、火狐浏览器等等各大浏览器显示。 免费制作 为用户使用方便考虑,全自动网页制作系统无需繁琐的注册与登入,直…...
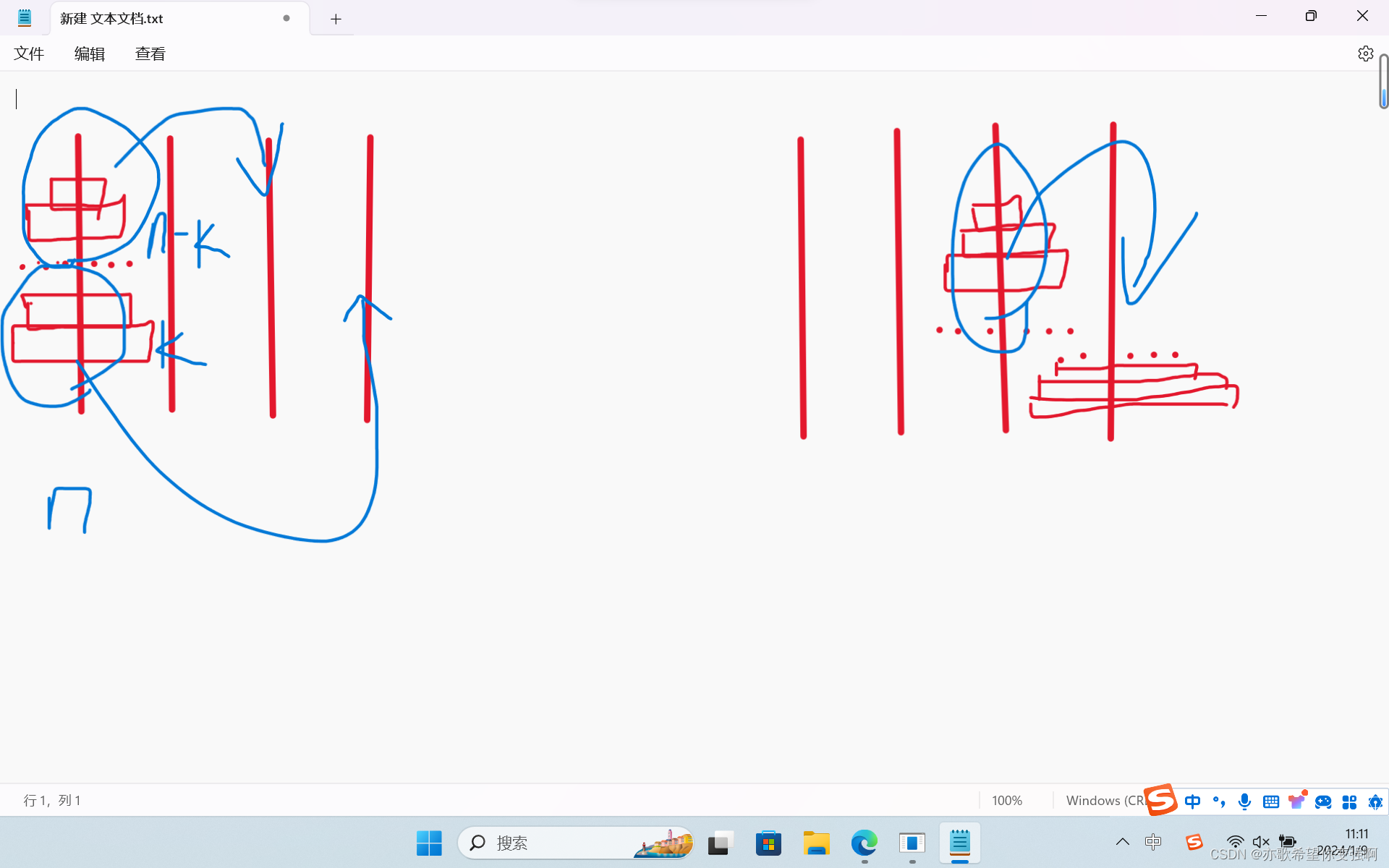
【算法每日一练]-动态规划 (保姆级教程 篇16) #纸带 #围栏木桩 #四柱河内塔
目录 今日知识点: 计算最长子序列的方案个数,类似最短路径个数问题 四柱河内塔问题:dp[i]min{ (p[i-k]f[k])dp[i-k] } 纸带 围栏木桩 四柱河内塔 纸带 思路: 我们先设置dp[i]表示从i到n的方案数。 那么减法操作中ÿ…...

Grounding 模型 + SAM 报错
引入 Grounding 目标检测模型串联 SAM 从而实现实例分割任务,目前支持 Grounding DINO 和 GLIP 参考教程 MMDetection-SAM 如果是 Grounding DINO 则安装如下依赖即可 cd playground pip install githttps://github.com/facebookresearch/segment-anything.git pip…...
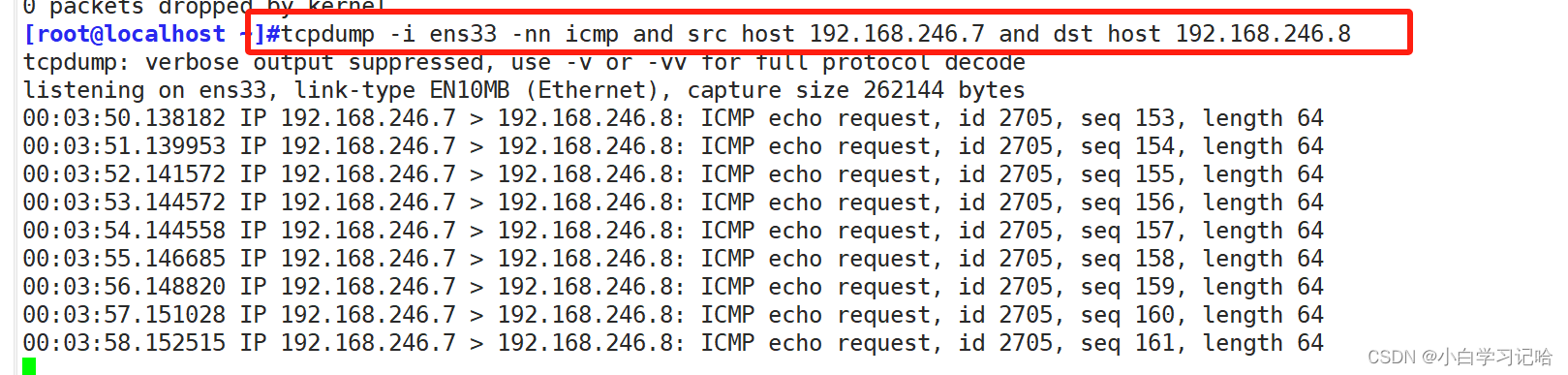
linux 网络基础配置
将Linux主机接入到网络,需要配置网络相关设置一般包括如下内容: 主机名 iP/netmask (ip地址,网关) 路由:默认网关 网络连接状态 DNS服务器 (主DNS服务器 次DNS服务器 第三个DNS服务器) 一、…...

leetcode-相同的树
100. 相同的树 使用递归的方法 # Definition for a binary tree node. # class TreeNode: # def __init__(self, val0, leftNone, rightNone): # self.val val # self.left left # self.right right class Solution:def isSameTree(self, p: …...
)
Leetcode17-好数对的数目(1512)
1、题目 给你一个整数数组 nums 。 如果一组数字 (i,j) 满足 nums[i] nums[j] 且 i < j ,就可以认为这是一组 好数对 。 返回好数对的数目。 示例 1: 输入:nums [1,2,3,1,1,3] 输出:4 解释:有 4 组好数对&am…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...