当前位置： 首页 > news >正文

网站媒体给房开做内容推广/网络推广的方法你知道几个?

news 文章来源：https://blog.csdn.net/anlog/article/details/135514907 2025/3/10 4:02:25
网站媒体给房开做内容推广,网络推广的方法你知道几个?,网站 流程,付公司制作网站费怎么做凭证图片转换为鼠标光标代码如下： private void Form1_Load(object sender, EventArgs e) {//button1.Cursor System.Windows.Forms.Cursors.Hand;Bitmap bmp new Bitmap("780.jpg");Cursor cursor new Cursor(bmp.GetHicon());button1.Cursor cursor;} …

图片转换为鼠标光标代码如下：

private void Form1_Load(object sender, EventArgs e)
{//button1.Cursor = System.Windows.Forms.Cursors.Hand;Bitmap bmp = new Bitmap("780.jpg");Cursor cursor = new Cursor(bmp.GetHicon());button1.Cursor = cursor;}

注意事项：图片尽量使用png格式（支持透明） 

参考

如何管理鼠标指针 - Windows Forms .NET | Microsoft Learnicon-default.png?t=N7T8https://learn.microsoft.com/zh-cn/dotnet/desktop/winforms/input-mouse/how-to-manage-cursor-pointer?view=netdesktop-8.0

特此记录

anlog

2024年1月10日

相关文章：

c#图片作为鼠标光标

图片转换为鼠标光标代码如下： private void Form1_Load(object sender, EventArgs e) {//button1.Cursor System.Windows.Forms.Cursors.Hand;Bitmap bmp new Bitmap("780.jpg");Cursor cursor new Cursor(bmp.GetHicon());button1.Cursor cursor;} …...

编程日记 2024/1/12 5:12:59

微信小程序swiper实现层叠轮播图

在微信小程序中,需要实现展示5个，横向层叠的轮播图效果，轮播图由中间到2侧的依次缩小.如下图 使用原生小程序进行开发,没有使用Skyline模式，所以layout-type配置项也无效。所以基于swiper组件进行调整。 主要思路就是设置不同的样式&#xff…...

编程日记 2024/1/12 5:10:57

揭露欧拉骗局第二篇：逼近公式“Σ1/n=lnn+C”。

Σ1/nlnnC是欧拉为调和级数创造(注意是创造、而不是发现)的“逼近公式”，它在欧系大名鼎鼎，因为它解决了欧洲人百筹莫展的“调和级数求和问题”。 “lnnC”是欧拉的发明，欧拉认为n→∞时，Σ1/nlnn常数，这个常数就是欧…...

编程日记 2024/1/12 5:08:55

MYSQL的学习——单行函数详解

目录 1. 数值函数 1) 基本函数 2) 角度与弧度互换函数 3) 三角函数 4) 指数与对数函数 5) 进制间的转换 2. 字符串函数 3. 日期和时间函数 1) 获取日期、时间 2) 日期与时间戳的转换 3) 获取月份、星期、星期数、天数等函数 4) 日期的操作函数 5) 时间和秒钟转换的…...

编程日记 2024/1/12 5:07:54

深度解析Cron表达式：精确控制任务调度的艺术

深度解析Cron表达式：精确控制任务调度的艺术 希望我们都可以满怀期待的路过每一个转角 去遇见 那个属于自己故事的开始 去追寻那个最真实的自己 去放下 去拿起 安然，自得，不受世俗牵绊… 导言 在计算机科学领域，任务调度是一项关…...

编程日记 2024/1/12 5:06:53

java实现AES256对称加解密工具类

一、引入依赖包 引入相关依赖包 <dependency><groupId>org.bouncycastle</groupId><artifactId>bcprov-jdk15on</artifactId><version>1.70</version> </dependency> <!--lombok用于简化实体类开发--> <dependency&g…...

编程日记 2024/1/12 5:04:51

其他排序（基数排序，希尔排序和桶排序）（数据结构课设篇3，python版）（排序综合）

本篇博客主要详细讲解一下其他排序&#xff08;基数排序&#xff0c;希尔排序和桶排序&#xff09;也是排序综合系列里最后一篇博客。第一篇博客讲解的是LowB三人组&#xff08;冒泡排序&#xff0c;插入排序&#xff0c;选择排序&#xff09;&#xff08;数据结构课设篇1&…...

编程日记 2024/1/12 5:03:50

【复现】DiffTalk

code&#xff1a;GitHub - sstzal/DiffTalk: [CVPR2023] The implementation for "DiffTalk: Crafting Diffusion Models for Generalized Audio-Driven Portraits Animation" 问题1. ERROR: Failed building wheel for pysptk Cython.Compiler.Errors.CompileError:…...

编程日记 2024/1/12 5:01:48

SQLServer 系统概述

目录 1.SQL语言的发展和特点 2.SQL语言的特点 1.SQL语言的发展和特点 SQL是利用一些简单的语句构成的基本语法&#xff0c;来存储数据库的内容。目前已经成为关系型数据库系统中使用最广泛的语言。 1974年SQL语言由Boyce和Chamberlin提出来。 1975~1979年研制了著名的关系数…...

编程日记 2024/1/12 4:59:44

Vue3 + TS + Element-Plus —— 项目系统中封装表格+搜索表单 十分钟写五个UI不在是问题

前期回顾 纯前端 —— 200行JS代码、实现导出Excel、支持DIY样式&#xff0c;纵横合并-CSDN博客https://blog.csdn.net/m0_57904695/article/details/135537511?spm1001.2014.3001.5501 目录 一、&#x1f6e0;️ newTable.vue 封装Table 二、&#x1f6a9; newForm.vue …...

编程日记 2024/1/12 4:57:42

Linux系统——测试端口连通性方法

目录 一、TCP端口连通性测试 1、ssh 2、telnet&#xff08;可能需要安装&#xff09; 3、curl 4、tcping&#xff08;需要安装&#xff09; 5、nc&#xff08;需要安装&#xff09; 6、nmap&#xff08;需要安装&#xff09; 二、UDP端口连通性测试 1、nc&#xff08;…...

编程日记 2024/1/12 4:56:41

Python虚拟环境轻松配置：Jupyter Notebook中的内核管理指南

问题 在Python开发中&#xff0c;一些人在服务器上使用Jupyter Notebook中进行开发。一般是创建虚拟环境后&#xff0c;向Jupyter notebook中添加虚拟环境中的Kernel&#xff0c;后续新建Notebook中在该Kernel中进行开发&#xff0c;这里记录一下如何创建Python虚拟环境以及添…...

编程日记 2024/1/12 4:55:39

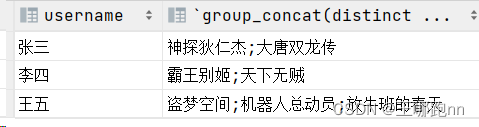
大数据-hive函数与mysql函数的辨析及练习-将多行聚合成一行

目录 1. &#x1f959;collect_list: 聚合-不去重 2. &#x1f959;collect_set(col): 聚合-去重 3. &#x1f959;mysql的聚合函数-group_concat 4. leetcode练习题 1. &#x1f959;collect_list: 聚合-不去重 将组内的元素收集成数组 不会去重 2. &#x1f959;collec…...

编程日记 2024/1/12 4:54:38

【AI视野·今日NLP 自然语言处理论文速览 第七十三期】Tue, 9 Jan 2024

AI视野今日CS.NLP 自然语言处理论文速览 Tue, 9 Jan 2024 Totally 80 papers &#x1f449;上期速览✈更多精彩请移步主页 Daily Computation and Language Papers FFSplit: Split Feed-Forward Network For Optimizing Accuracy-Efficiency Trade-off in Language Model Infe…...

编程日记 2024/1/12 4:53:37

vue知识-03

购物车案例 要实现的功能&#xff1a; 1、计算商品总价格 2、全选框和取消全选框 3、商品数量的增加和减少 <body> <div id"app"><div class"row"><div class"col-md-6 col-md-offset-3"><h1 class"text-center…...

编程日记 2024/1/12 4:52:36

关于httpClient 使用的注意事项

关于httpClient 使用的注意事项 用例 PoolingHttpClientConnectionManager connectionManager new PoolingHttpClientConnectionManager();// 最大连接数-不设置默认20connectionManager.setMaxTotal(200);// 每个路由最大连接数-不设置默认2connectionManager.setDefaultMax…...

编程日记 2024/1/12 4:49:32

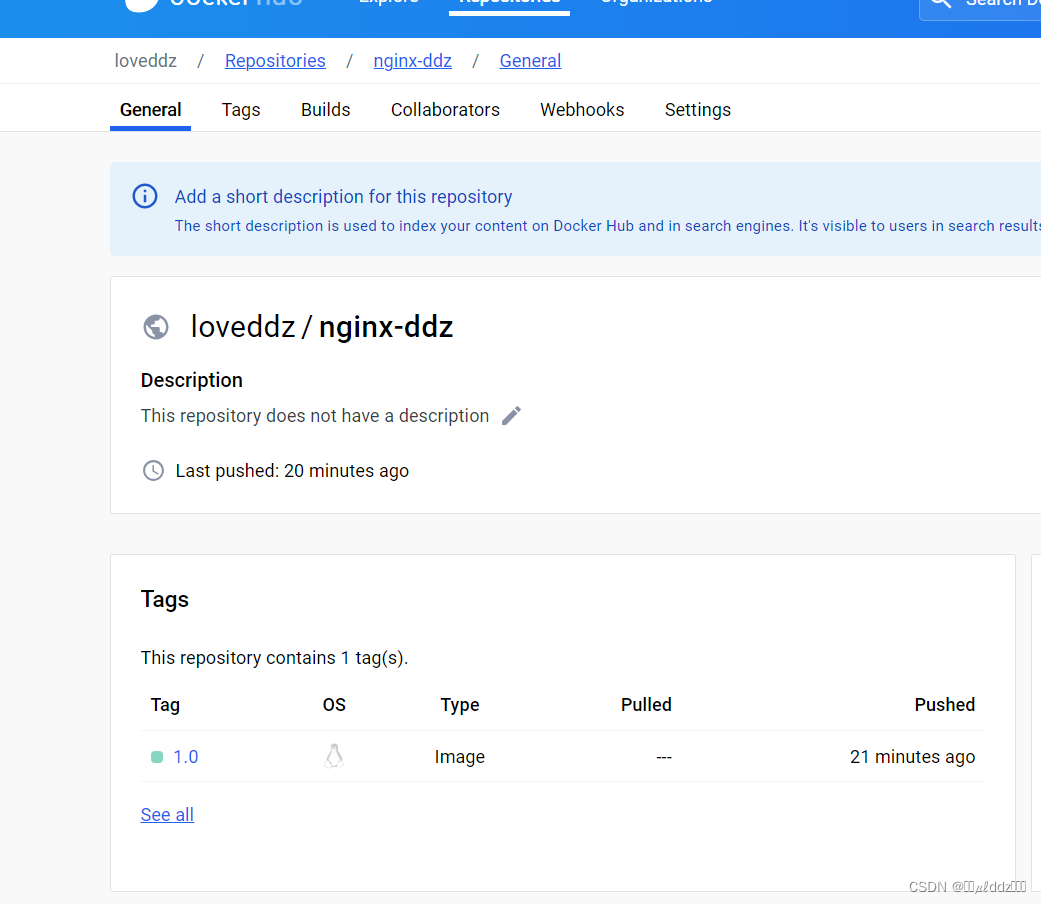
Docker 发布自定义镜像到公共仓库

Docker 发布自定义镜像到公共仓库 引言 Docker 是一种轻量级、便携式的容器化技术&#xff0c;可以使应用程序在不同环境中更加可移植。在本文中&#xff0c;我们将学习如何使用 Docker 从公共仓库拉取 Nginx 镜像&#xff0c;定制该镜像&#xff0c;添加自定义配置文件&…...

编程日记 2024/1/12 4:48:31

程序员有哪些接单的渠道？

这题我会&#xff01;程序员接单的渠道那可太多了&#xff0c;想要接到合适的单子&#xff0c;筛选一个合适的平台很重要。如果你也在寻找一个合适的接单渠道&#xff0c;可以参考以下这些方向。 首先&#xff0c;程序员要对接单有一个基本的概念&#xff1a;接单渠道可以先粗略…...

编程日记 2024/1/12 4:47:30

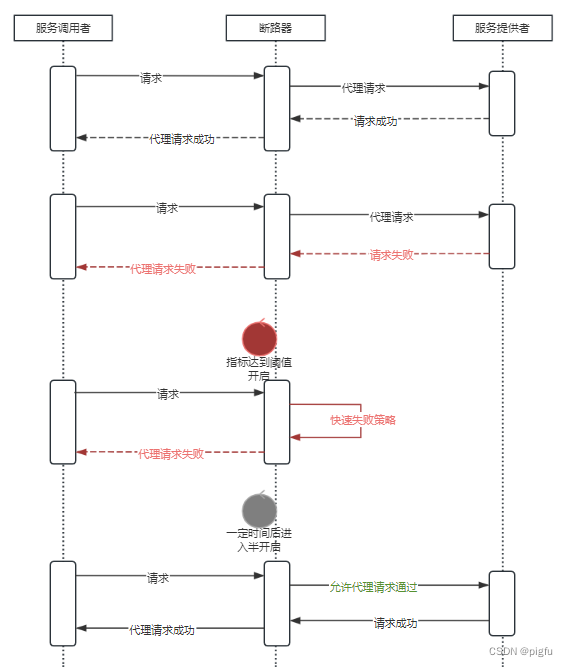
服务容错-熔断策略之断路器hystrix-go

文章目录 概要一、服务熔断二、断路器模式三、hystrix-go3.1、使用3.2、源码 四、参考 概要 微服务先行者Martin Fowler与James Lewis在文章microservices中指出了微服务的九大特征&#xff0c;其中一个便是容错性设计(Design for failure)。正如文章中提到的&#xff0c;微服…...

编程日记 2024/1/12 4:46:29

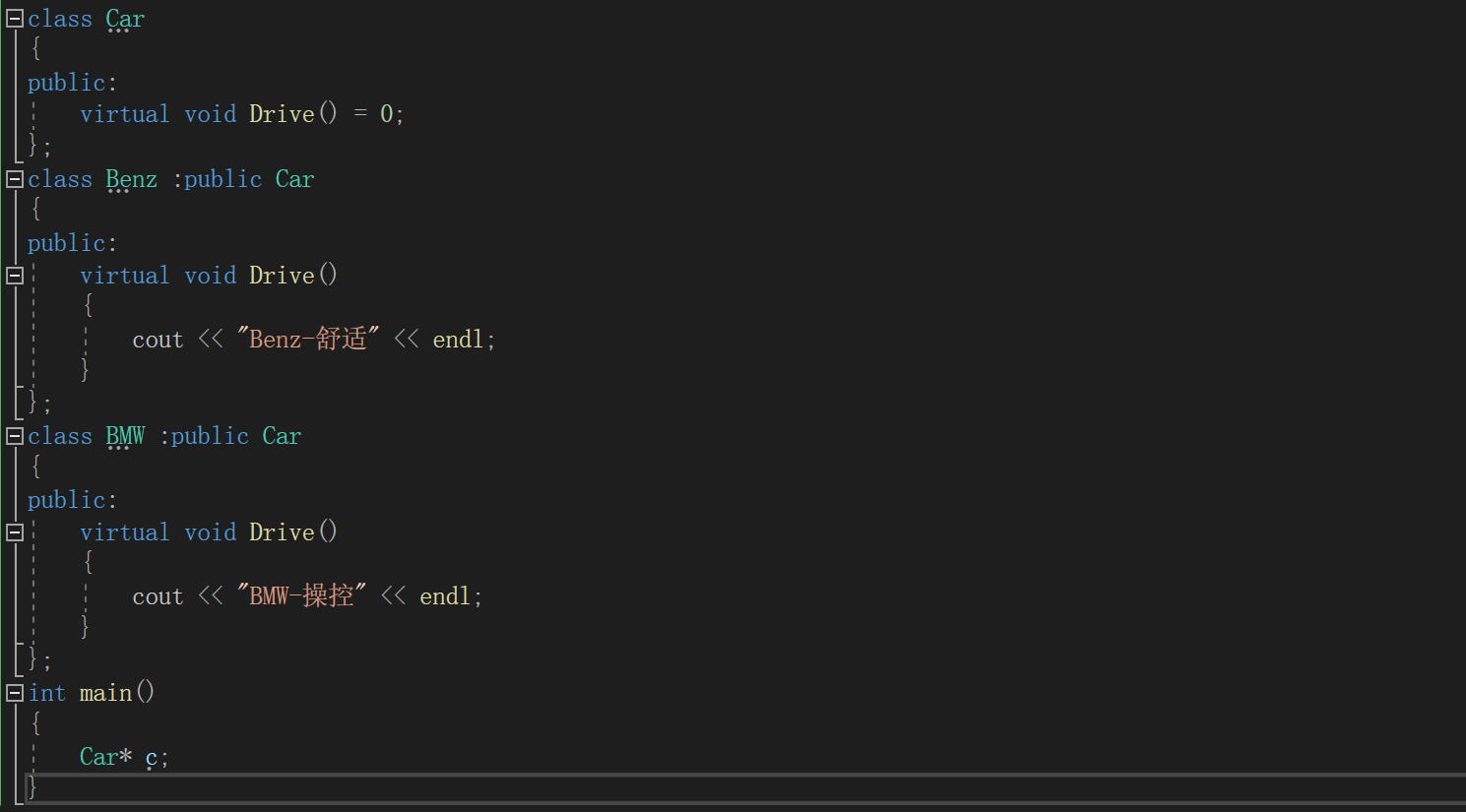
C++进阶（三）多态

&#x1f4d8;北尘_&#xff1a;个人主页 &#x1f30e;个人专栏:《Linux操作系统》《经典算法试题 》《C》 《数据结构与算法》 ☀️走在路上&#xff0c;不忘来时的初心 文章目录 一、多态的概念1、概念 二、多态的定义及实现1、多态的构成条件2、虚函数3、虚函数的重写4、C…...

编程日记 2024/1/12 4:45:28

大众汽车宣布将ChatGPT，批量集成在多种汽车中！

1月9日&#xff0c;大众汽车在官网宣布&#xff0c;将ChatGPT批量集成到电动、内燃机汽车中。 大众表示&#xff0c;将ChatGPT与其IDA语音助手相结合&#xff0c;用户通过自然语言就能与ChatGPT进行互动&#xff0c;例如&#xff0c;帮我看看最近的三星米其林饭店在哪里&#…...

编程日记 2024/1/12 4:42:23

React----函数组件和类组件

函数组件与类组件&#xff1a;React 中的两种组件风格 React 是一个用于构建用户界面的流行 JavaScript 库&#xff0c;其中组件是构建块的基本单元。在 React 中&#xff0c;有两种主要的组件风格&#xff1a;函数组件和类组件。本文将使用TypeScript介绍它们的用法、区别以及…...

编程日记 2024/1/12 4:40:22

Kafka集群部署 (KRaft模式集群)

KRaft 模式是 Kafka 在 3.0 版本中引入的新模式。KRaft 模式使用了 Raft 共识算法来管理 Kafka 集群元数据。Raft 算法是一种分布式共识算法&#xff0c;具有高可用性、可扩展性和安全性等优势。 在 KRaft 模式下&#xff0c;Kafka 集群中的每个 Broker 都具有和 Zookeeper 类…...

编程日记 2024/1/12 4:39:20

Vue 自定义仿word表单录入之日期输入组件

因项目需要&#xff0c;要实现仿word方式录入数据&#xff0c;要实现鼠标经过时才显示编辑组件&#xff0c;预览及离开后则显示具体的文字。 鼠标经过时显示 正常显示及离开时显示 组件代码 <template ><div class"paper-input flex flex-col border-box "…...

编程日记 2024/1/12 4:37:18

Oracle与Java JDBC数据类型对照

Oracle Database JDBC开发人员指南和参考 SQL Data TypesJDBC Type CodesStandard Java TypesOracle Extension Java Types CHAR java.sql.Types.CHAR java.lang.String oracle.sql.CHAR VARCHAR2 java.sql.Types.VARCHAR java.lang.String oracle.sql.CHAR LONG jav…...

编程日记 2024/1/12 4:36:18

C++力扣题目226--翻转二叉树

给你一棵二叉树的根节点 root &#xff0c;翻转这棵二叉树&#xff0c;并返回其根节点。 示例 1&#xff1a; 输入&#xff1a;root [4,2,7,1,3,6,9] 输出&#xff1a;[4,7,2,9,6,3,1]示例 2&#xff1a; 输入&#xff1a;root [2,1,3] 输出&#xff1a;[2,3,1]示例 3&#x…...

编程日记 2024/1/12 4:35:16

Gorm 数据库表迁移与表模型定义

文章目录 一、Docker快速创建MySQL实例1.1 创建1.3 创建数据库 二、AutoMigrate介绍与使用2.1 AutoMigrate介绍2.2 AutoMigrate 基本使用 三、模型定义3.1 模型定义3.2 快速增删改查3.3 约定3.4 gorm.Model 四、表模型主键、表名、列名的约定4.1 主键&#xff08;Primary Key&a…...

编程日记 2024/1/12 4:34:15

系列三、Spring Security中自定义用户名/密码

一、Spring Security中自定义用户名/密码 1.1、自定义用户名/密码 1.1.1、配置文件中配置 spring.security.user.nameroot spring.security.user.password123456 1.1.2、定义基于内存的用户 /*** Author : 一叶浮萍归大海* Date: 2024/1/11 21:50* Description:*/ Configu…...

编程日记 2024/1/12 4:32:12

如何顺滑使用华为云编译构建平台？

这两年平台构建服务需求越来越大&#xff0c;却一直苦于找不到一些指南&#xff0c; 这里特意写了一篇&#xff0c; 对在学习代码阶段和新手程序员朋友也蛮友好&#xff0c; 配置真的也不难&#xff0c; 也特别适合想尝试从0到1做个APP的朋友了。 以华为云的CodeArts Build为例…...

编程日记 2024/1/12 4:31:10

查看Linux磁盘空间

(1)、该命令会列出当前系统所有挂载的文件系统以及它们的使用情况&#xff0c;包括总容量、已用空间、可用空间、使用百分比等信息 df -h如果查看某一个文件夹的,可以 df -h folderName (2)、计算指定目录下所有文件和子目录所占用的磁盘空间大小&#xff0c;并以人类可读的格…...

编程日记 2024/1/12 4:29:08