当前位置： 首页 > news >正文

基于Vue组合式API的实用工具集

news 2026/2/8 21:04:42

简介

今天，给大家分享一个很实用的工具库 VueUse，它是基于 Vue Composition Api，也就是组合式API。支持在Vue2和Vue3项目中进行使用，据说是目前世界上Star最高的同类型库之一。

图片

图片

官方地址：https://vueuse.org/

中文地址：https://www.vueusejs.com/

github：https://github.com/vueuse/vueuse

功能目录

图片

图片

链接地址：https://www.vueusejs.com/guide/

功能演示

白天黑夜模式切换

使用工具的useColorMode实现黑白模式的切换。

图片</

相关文章：

基于Vue组合式API的实用工具集

简介 今天，给大家分享一个很实用的工具库 VueUse，它是基于 Vue Composition Api，也就是组合式API。支持在Vue2和Vue3项目中进行使用，据说是目前世界上Star最高的同类型库之一。 图片 官方地址：https://vueuse.org/ 中文地址：https://www.vueusejs.com/ github：https…...

编程日记 2024/1/12 13:09:56

065：vue中将一维对象数组转换为二维对象数组

第065个 查看专栏目录: VUE ------ element UI 专栏目标 在vue和element UI联合技术栈的操控下&#xff0c;本专栏提供行之有效的源代码示例和信息点介绍&#xff0c;做到灵活运用。 &#xff08;1&#xff09;提供vue2的一些基本操作&#xff1a;安装、引用&#xff0c;模板使…...

编程日记 2024/1/12 13:07:54

mysql 字符串分割

目录 前言substring_indexsubstring_index 特性字符串分割 前言 略 substring_index 正向截取字符串 mysql> select substring_index(www.baidu.com,.,1); ---------------------------------------- | substring_index(www.baidu.com,.,1) | -------------------------…...

编程日记 2024/1/12 13:04:51

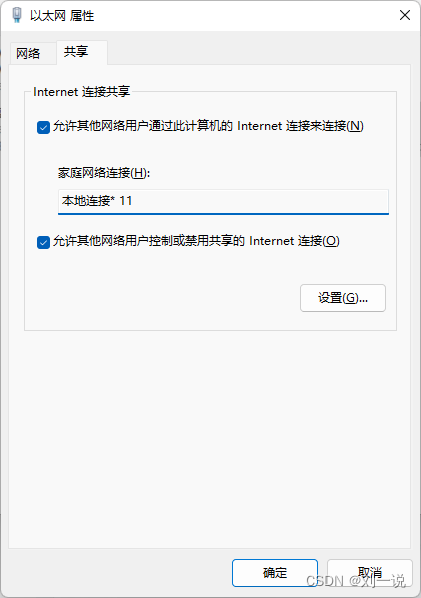
解决Windows11 “我们无法设置移动热点”

目录 问题复现解决办法①启动网络适配器②打开移动热点③共享网络连接④连接移动热点总结 问题复现 因为交换机上网口限制&#xff0c;开发环境暂时没有WIFI设备&#xff0c;只有一根网线和一台笔记本电脑。于是开启笔记本电脑的WiFi共享服务。结果提示 “我们无法设置移动热点…...

编程日记 2024/1/12 13:03:50

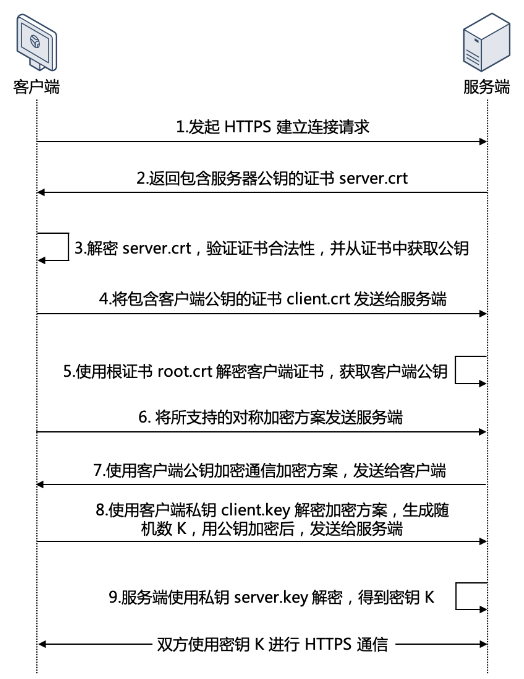
python tcp socket中实现SSL/TLS认证

SSL/TLS介绍 官话说SSL是安全套接层(secure sockets layer)&#xff0c;TLS是SSL的继任者&#xff0c;叫传输层安全(transport layer security)。 说白点&#xff0c;就是在明文的上层和TCP层之间加上一层加密&#xff0c;这样就保证上层信息传输的安全。如HTTP协议是明文传输…...

编程日记 2024/1/12 13:02:50

SQL-修改表操作

&#x1f389;欢迎您来到我的MySQL基础复习专栏 ☆* o(≧▽≦)o *☆哈喽~我是小小恶斯法克&#x1f379; ✨博客主页&#xff1a;小小恶斯法克的博客 &#x1f388;该系列文章专栏&#xff1a;重拾MySQL &#x1f379;文章作者技术和水平很有限&#xff0c;如果文中出现错误&am…...

编程日记 2024/1/12 12:59:47

【Node.js学习 day3——http模块】

创建HTTP服务端 //1.导入http模块 const http require(http);//2.创建服务对象 const server http.createServer((request, response) > {response.end(Hello HTTP Server);//设置响应体 });//3.监听端口&#xff0c;启动服务 server.listen(9000,()>{console.log(服务…...

编程日记 2024/1/12 12:56:44

初探UAF漏洞（3）

构造exp #include <iostream> #include <Windows.h>typedef void(*FunctionPointer) ();typedef struct _FAKE_USE_AFTER_FREE {FunctionPointer countinter;char bufffer[0x54]; }FAKE_USE_AFTER_FREE, * PUSE_AFTER_FREE;void ShellCode() {_asm{noppushadmov e…...

编程日记 2024/1/12 12:55:44

C++学习笔记（二十一）

一、set/multiset容器 1. set基本概念 简介&#xff1a;所有元素都会在插入时自动被排序 本质&#xff1a;set/multiset属于关联式容器&#xff0c;底层结构是用二叉树实现的 set和multiset的区别&#xff1a;set不允许容器中有重复的元素&#xff0c;multiset允许容器中有…...

编程日记 2024/1/12 12:54:43

Java版企业电子招投标系统源代码，支持二次开发，采用Spring cloud技术

在数字化时代&#xff0c;采购管理也正经历着前所未有的变革。全过程数字化采购管理成为了企业追求高效、透明和规范的关键。该系统通过Spring Cloud、Spring Boot2、Mybatis等先进技术&#xff0c;打造了从供应商管理到采购招投标、采购合同、采购执行的全过程数字化管理。通过…...

编程日记 2024/1/12 12:53:42

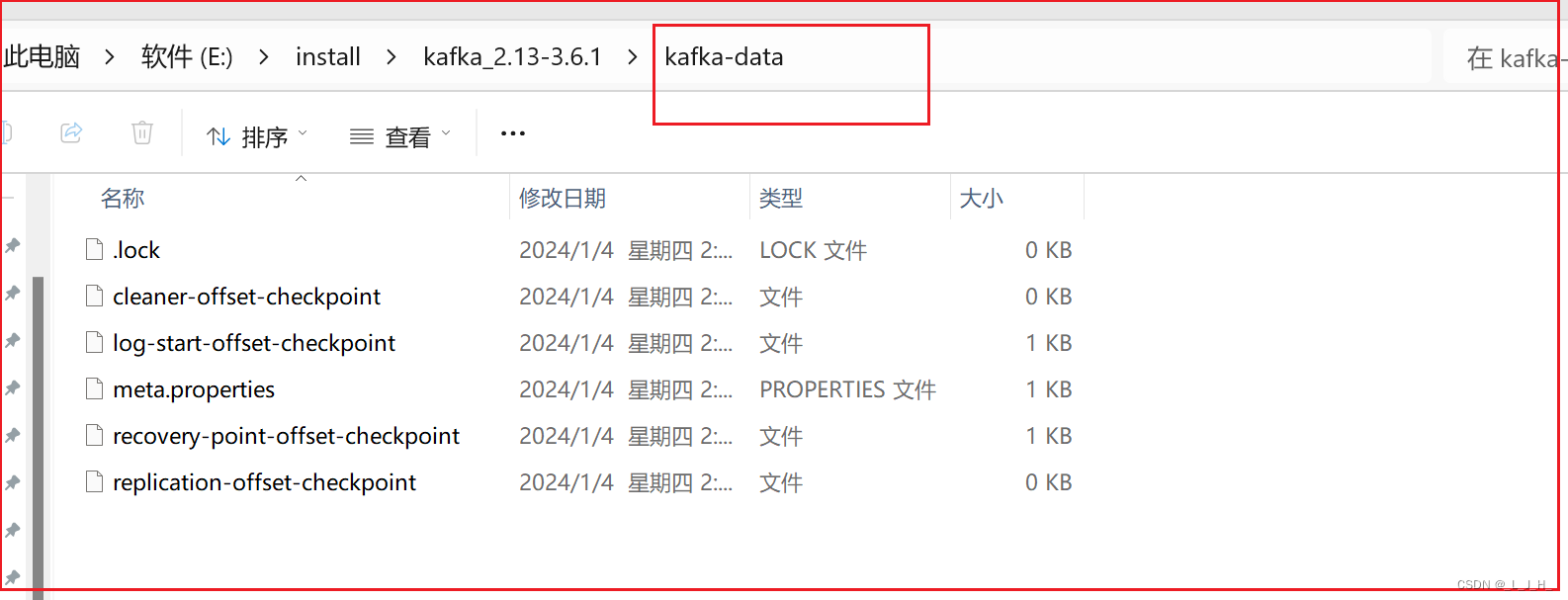
01、Kafka ------ 下载、安装 ZooKeeper 和 Kafka

目录 Kafka是什么&#xff1f;安装 ZooKeeper下载安装启动 zookeeper 服务器端启动 zookeeper 的命令行客户端工具 安装 Kafka下载安装启动 Kafka 服务器 Kafka是什么&#xff1f; RabbitMQ的性能比ActiveMQ的性能有显著提升。 Kafka的性能比RabbitMQ的性能又有显著提升。 K…...

编程日记 2024/1/12 12:51:40

Spark: 检查数据倾斜的方法以及解决方法总结

1. 使用Spark UI Spark UI提供了一个可视化的方式来监控和调试Spark作业。你可以通过检查各个Stage的任务执行时间和数据大小来判断是否存在数据倾斜。 任务执行时间: 如果某个Stage中的大部分任务很快完成&#xff0c;但有少数任务执行时间非常长&#xff0c;这可能是数据倾…...

编程日记 2024/1/12 12:50:39

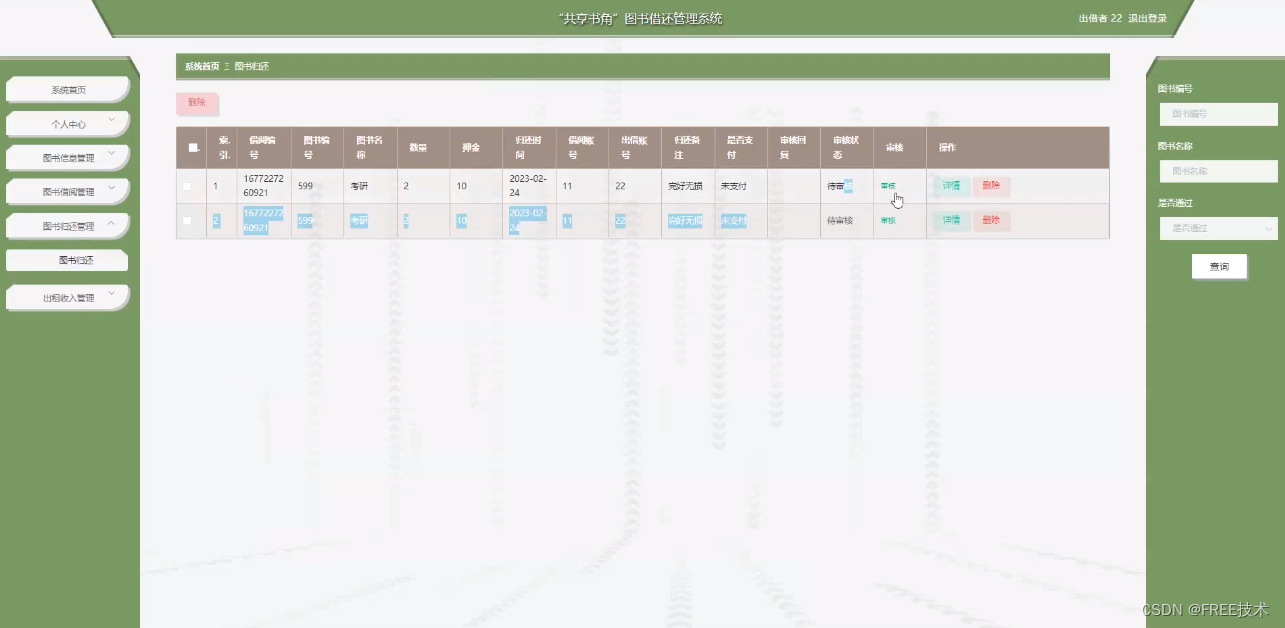
基于JavaWeb+BS架构+SpringBoot+Vue“共享书角”图书借还管理系统系统的设计和实现

基于JavaWebBS架构SpringBootVue“共享书角”图书借还管理系统系统的设计和实现 文末获取源码Lun文目录前言主要技术系统设计功能截图订阅经典源码专栏Java项目精品实战案例《500套》 源码获取 文末获取源码 Lun文目录 第1章 概 述 5 1.1 开发背景及研究意义 5 1.2 国内外研究…...

编程日记 2024/1/12 12:47:36

论文阅读：TinyGPT-V 论文阅读及源码梳理对应

&#xff01;&#xff01;&#xff01;目前只是初稿&#xff0c;静待周末更新 引言 TinyGPT-V来自论文&#xff1a;TinyGPT-V: Efficient Multimodal Large Language Model via Small Backbones&#xff0c;是一篇基于较小LLM作为backbone的多模态工作。相关工作已经开源&…...

编程日记 2024/1/12 12:45:34

XCTF：MISCall[WriteUP]

使用file命令&#xff0c;查看该文件类型 file d02f31b893164d56b7a8e5edb47d9be5 文件类型&#xff1a;bzip2 使用bzip2命令可对该文件进行解压 bzip2 -d d02f31b893164d56b7a8e5edb47d9be5 生成了一个后缀为.out的文件 再次使用file命令&#xff0c;查看该文件类型 file…...

编程日记 2024/1/12 12:43:33

【MIdjourney】图像角度关键词

本篇仅是我个人在使用过程中的一些经验之谈&#xff0c;不代表一定是对的&#xff0c;如有任何问题欢迎在评论区指正&#xff0c;如有补充也欢迎在评论区留言。 1.侧面视角(from side) 侧面视角观察或拍摄的主体通常以其侧面的特征为主要焦点&#xff0c;以便更好地展示其轮廓…...

编程日记 2024/1/12 12:42:32

使用 Jamf Pro 和 Okta 工作流程实现自动化苹果设备管理

Jamf的销售工程师Vincent Bonnin与Okta的产品经理Emily Wendell一起介绍了JNUC 2021的操作方法会议。它们涵盖了Okta工作流程&#xff08;Okta Workflow&#xff09;&#xff0c;并在其中集成了Jamf Pro&#xff0c;构建了一些工作流程&#xff0c;并提供了几个用例。 Okta 工作…...

编程日记 2024/1/12 12:40:30

根能抵达的节点（二分法、DFS）C++

给定一棵由 N个节点构成的带边权树。节点编号从 0到 N−1&#xff0c;其中 0 号点为根节点。最初&#xff0c;从根节点可以抵达所有节点&#xff08;包括自己&#xff09;。如果我们将所有边权小于 X 的边全部删掉&#xff0c;那么从根节点可以抵达的节点数目就可能发生改变。 …...

编程日记 2024/1/12 12:39:30

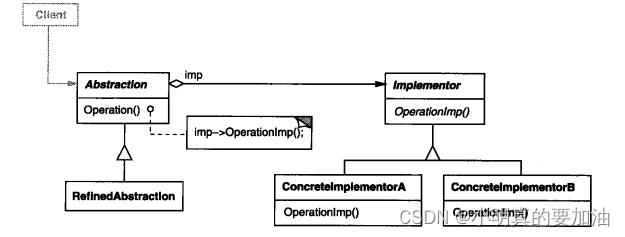
一天一个设计模式---桥接模式

概念 桥接器模式是一种结构型设计模式&#xff0c;旨在将抽象部分与实现部分分离&#xff0c;使它们可以独立变化而不相互影响。桥接器模式通过创建一个桥接接口&#xff0c;连接抽象和实现&#xff0c;从而使两者可以独立演化。 具体内容 桥接器模式通常包括以下几个要素&a…...

编程日记 2024/1/12 12:37:28

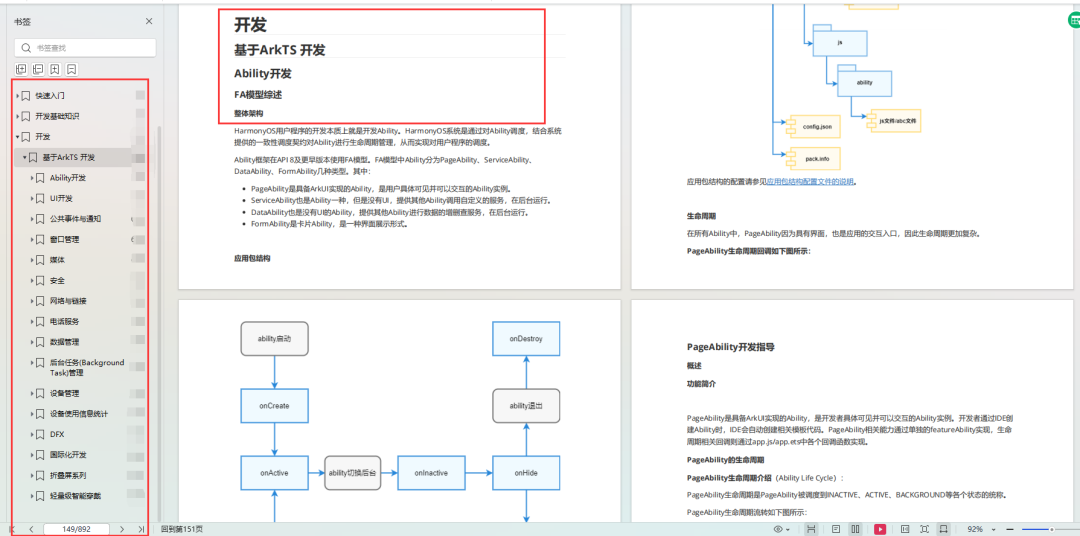
OpenHarmony4.0Release系统应用常见问题FAQ

前言 自OpenHarmony4.0Release发布之后&#xff0c;许多小伙伴使用了配套的系统应用源码以及IDE作为基线开发&#xff0c;也遇到了各种各样的问题&#xff0c;这篇文档主要收录了比较常见的一些问题解答。 FAQ 系统应用源码在哪 目前OpenHarmony系统应用分为3种模式&#x…...

编程日记 2024/1/12 12:36:27

51c自动驾驶~合集58

我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留&#xff0c;CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制&#xff08;CCA-Attention&#xff09;&#xff0c;…...

编程新知 2026/2/5 4:25:15

React hook之useRef

React useRef 详解 useRef 是 React 提供的一个 Hook&#xff0c;用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途&#xff0c;下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

编程新知 2025/6/11 15:21:26

最新SpringBoot+SpringCloud+Nacos微服务框架分享

文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的&#xff0c;根据Excel列的需求预估的工时直接打骨折&#xff0c;不要问我为什么&#xff0c;主要…...

编程新知 2026/2/1 23:39:12

如何理解 IP 数据报中的 TTL？

目录 前言理解 前言 面试灵魂一问&#xff1a;说说对 IP 数据报中 TTL 的理解&#xff1f;我们都知道&#xff0c;IP 数据报由首部和数据两部分组成&#xff0c;首部又分为两部分&#xff1a;固定部分和可变部分&#xff0c;共占 20 字节&#xff0c;而即将讨论的 TTL 就位于首…...

编程新知 2026/2/4 18:09:49

零基础在实践中学习网络安全-皮卡丘靶场（第九期-Unsafe Fileupload模块）（yakit方式）

本期内容并不是很难&#xff0c;相信大家会学的很愉快&#xff0c;当然对于有后端基础的朋友来说&#xff0c;本期内容更加容易了解&#xff0c;当然没有基础的也别担心&#xff0c;本期内容会详细解释有关内容 本期用到的软件&#xff1a;yakit&#xff08;因为经过之前好多期…...

编程新知 2026/1/21 12:29:04

【Go语言基础【13】】函数、闭包、方法

文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数&#xff08;函数作为参数、返回值&#xff09; 三、匿名函数与闭包1. 匿名函数&#xff08;Lambda函…...

编程新知 2025/12/8 19:02:25

AirSim/Cosys-AirSim 游戏开发（四）外部固定位置监控相机

这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机&#xff0c;因为在使用过程中发现 Airsim 对外部监控相机的描述模糊&#xff0c;而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置&#xff0c;最后在源码示例中找到了&#xff0c;所以感…...

编程新知 2026/2/5 18:58:39

如何更改默认 Crontab 编辑器 ？

在 Linux 领域中&#xff0c;crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用&#xff0c;用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益&#xff0c;允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

编程新知 2026/1/30 3:27:35

day36-多路IO复用

一、基本概念 &#xff08;服务器多客户端模型&#xff09; 定义&#xff1a;单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用&#xff1a;应用程序通常需要处理来自多条事件流中的事件&#xff0c;比如我现在用的电脑&#xff0c;需要同时处理键盘鼠标…...

编程新知 2026/1/31 7:42:50

归并排序：分治思想的高效排序

目录 基本原理 流程图解 实现方法 递归实现 非递归实现 演示过程 时间复杂度 基本原理 归并排序(Merge Sort)是一种基于分治思想的排序算法&#xff0c;由约翰冯诺伊曼在1945年提出。其核心思想包括&#xff1a; 分割(Divide)&#xff1a;将待排序数组递归地分成两个子…...

编程新知 2026/1/27 17:06:38