git 查看tag和创建tag以及上传tag命令
文章目录
- git 查看tag和创建tag以及上传tag命令
- git tag
- tag操作常用命令
git 查看tag和创建tag以及上传tag命令
git tag
如果你达到一个重要的阶段,并希望永远记住那个特别的提交快照,你可以使用 git tag 给它打上标签。
Git 的 tag 功能是一个非常有用的工具,它可以帮助开发者在代码仓库中标记重要的里程碑和版本号。
Tag 可以看作是一个快照,用于永久性地标记提交记录。它们通常用于发布新版本或里程碑,并且可以帮助开发者追踪项目的历史记录。Tag 在 Git 中是轻量级对象,不会像分支那样占用额外的存储空间,因此创建 Tag 对存储的影响很小。
tag操作常用命令
- 查看tag
git tag // 列出taggit tag -l // 列出taggit show 标签名 // 查看标签对应的提交git ls-remote --tags origin // 查询远程tags
- 添加标签
git tag -a 标签名称 -m 附注信息
git tag 标签名 提交版本commit号 // 基于某次提交创建tag
比如
git tag -a v0.1.0
创建带有说明的标签,用-a指定标签名,-m指定说明文字。
- 提交tag到远端服务器
git push origin 标签名称
- 通过tag创建新分支 (检出标签)
git checkout -b 分支名称 标签名称
相关文章:

git 查看tag和创建tag以及上传tag命令
文章目录 git 查看tag和创建tag以及上传tag命令git tagtag操作常用命令 git 查看tag和创建tag以及上传tag命令 git tag 如果你达到一个重要的阶段,并希望永远记住那个特别的提交快照,你可以使用 git tag 给它打上标签。 Git 的 tag 功能是一个非常有用…...
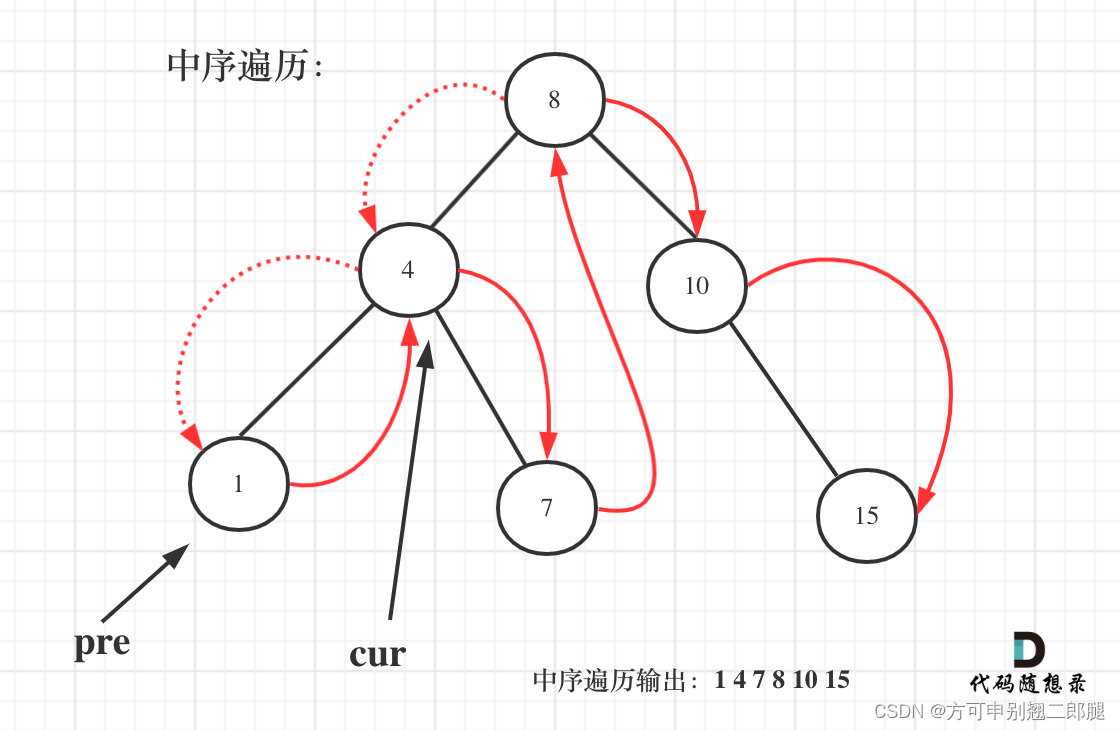
代码随想录二刷 |二叉树 | 二叉搜索树的最小绝对差
代码随想录二刷 |二叉树 | 二叉搜索树的最小绝对差 题目描述解题思路 & 代码实现递归法迭代法 题目描述 530.二叉搜索树的最小绝对差 给你一棵所有节点为非负值的二叉搜索树,请你计算树中任意两节点的差的绝对值的最小值。 示例&#…...

【Linux】Linux 系统编程——tree 命令
文章目录 1. 命令概述2. 命令格式3. 常用选项4. 相关描述4.1 tree 命令安装 5. 参考示例5.1 创建树形目录5.2 使用 tree 命令查看树形目录 1. 命令概述 tree 命令用于在命令行界面以树状图形式显示目录及其子目录的内容。这个命令递归地列出所有子目录,并可选择显示…...

Android简单控件
1.文本显示 设置文本内容的两种方式: 在XML文件中通过属性 android:text 设置文本 <resources><string name"app_name">chapter03</string><string name"hello">你好,世界</string> </resources&…...
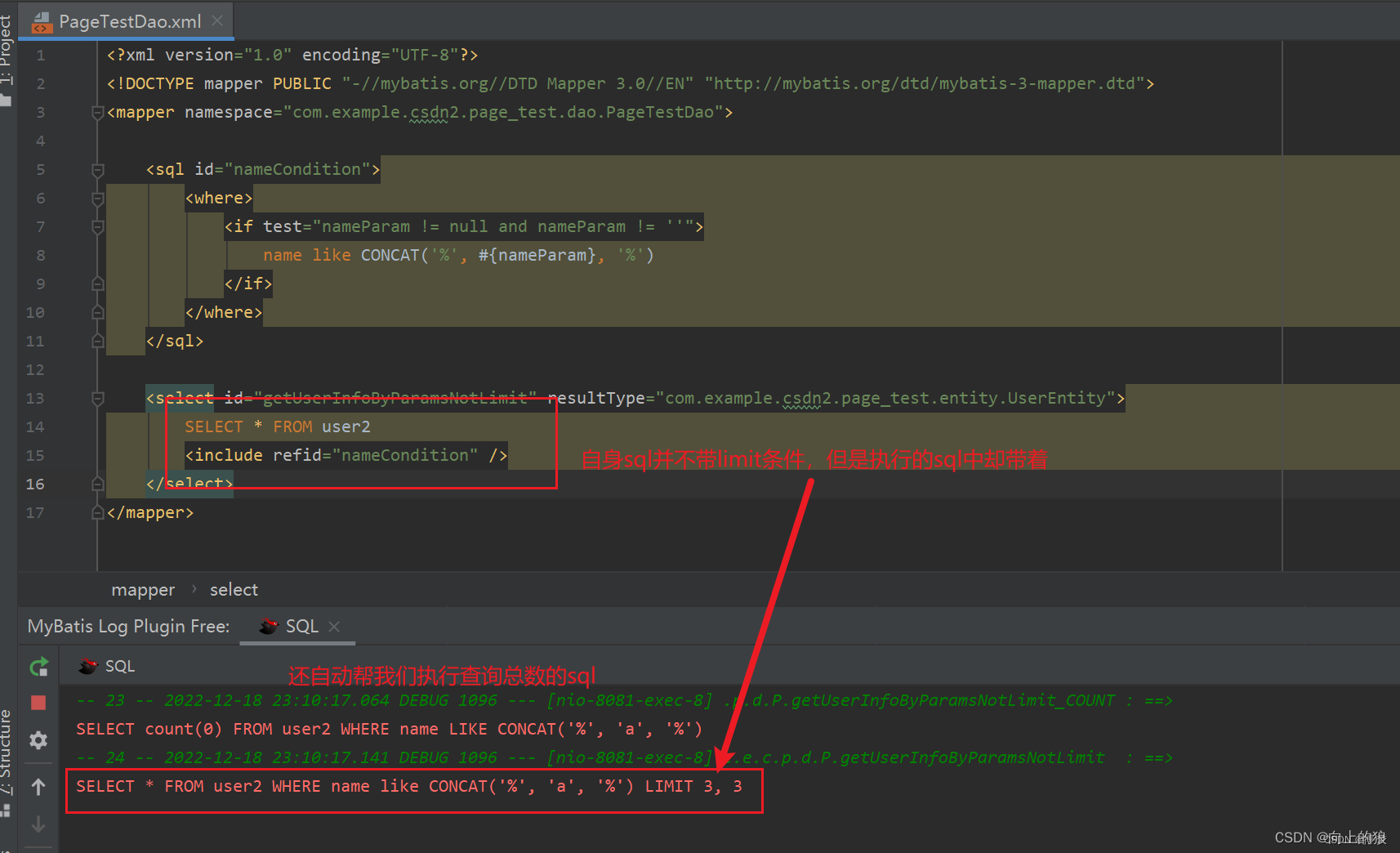
【Java 干货教程】Java实现分页的几种方式详解
一、前言 无论是自我学习中,还是在工作中,固然会遇到与前端搭配实现分页的功能,发现有几种方式,特此记录一下。 二、实现方式 2.1、分页功能直接交给前端实现 这种情况也是有的,(根据业务场景且仅仅只能用于数据量…...
关于Python里xlwings库对Excel表格的操作(三十一)
这篇小笔记主要记录如何【如何使用“Chart类”、“Api类"和“Axes函数”设置绘图区外框线型、颜色、粗细及填充颜色】。前面的小笔记已整理成目录,可点链接去目录寻找所需更方便。 【目录部分内容如下】【点击此处可进入目录】 (1)如何安…...

QML使用QCustomPlot笔记
这里在QML中使用QCustomPlot是定义一个继承自QQuickPaintedItem的类,它包含一个QCustomPlot对象,在paint函数中将这个对象转化为pixmap绘制到布局中显示。 在QML中使用QT的Widget控件也可以借鉴这个思路实现 顺便记录一下QCustomPlot的简单设置与使用。…...
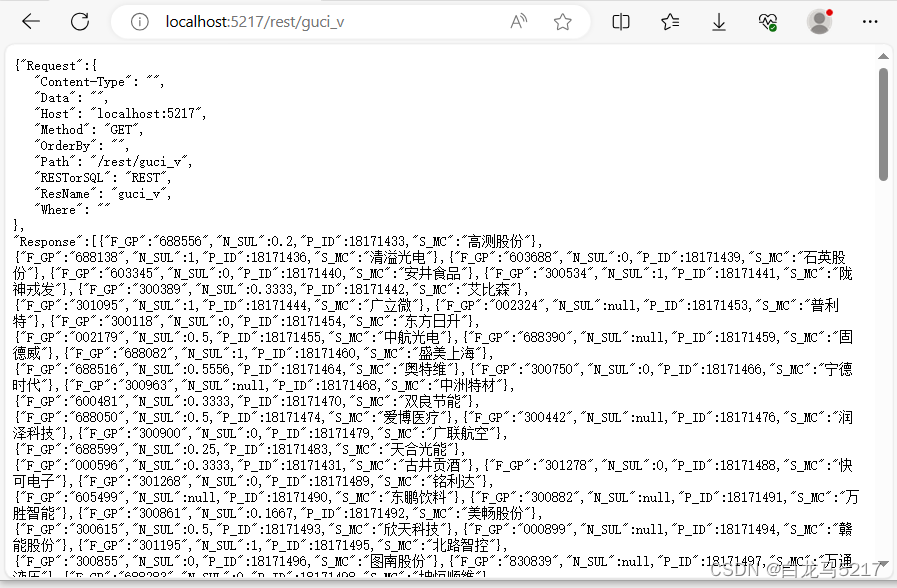
【REST2SQL】06 GO 跨包接口重构代码
【REST2SQL】01RDB关系型数据库REST初设计 【REST2SQL】02 GO连接Oracle数据库 【REST2SQL】03 GO读取JSON文件 【REST2SQL】04 REST2SQL第一版Oracle版实现 【REST2SQL】05 GO 操作 达梦 数据库 对所有关系数据的操作都只有CRUD,采用Go 的接口interface{}重构代码…...
《NLP入门到精通》栏目导读
一、说明 栏目《NLP入门到精通》本着从简到难得台阶式学习过度。将自然语言处理得知识贯穿过来。本栏目得前导栏目是《深度学习》、《pytorch实践》,因此,读者需要一定得深度学习基础,才能过度到此栏目内容。 二、博客建设理念 本博客基地&am…...

C++学习笔记——类继承
目录 一、一个简单的基类 1.1封装性 1.2继承性 1.3虚函数 1.4多态性 二、基类 2.1一个简单的C基类的示例 2.2 Animal是一个基类。 三、继承 3.1概念 3.2is-a关系 3.3多态公有继承 3.4静态联编和动态联编 3.5访问控制 3.6ABC理念 一、一个简单的基类 C中的基类是一…...

ARCGIS PRO SDK 使用条件管理 Pro UI
ARCGIS PRO UI简单介绍以下: 第一步:在Config.daml中在</AddInfo>标签下加上条件<conditions>标签(必须添加的) <conditions><!-- 定义条件 ,此处定义了两个--Tab 另一个为 group><insert…...

Halcon经典的边缘检测算子Sobel/Laplace/Canny
Halcon经典的边缘检测算子 文章目录 Halcon经典的边缘检测算子1. Sobel算子2. Laplace 算子3. Canny 算子4. 总结 关于边缘检测,有许多经典的算子,各大图形处理库都有各自的边缘检测算子,这里简要介绍几种。 1. Sobel算子 Sobel算子结合了高…...

用单片机设计PLC电路图
自记: 见另一篇文章,MOS驱动差了一个充电电容,栅极电容充电会有问题; 光耦用的直插,但板子用的贴片,此文档仅供参考 基本列出了PCB板情况,基础元器件,部分连接,原理等…...
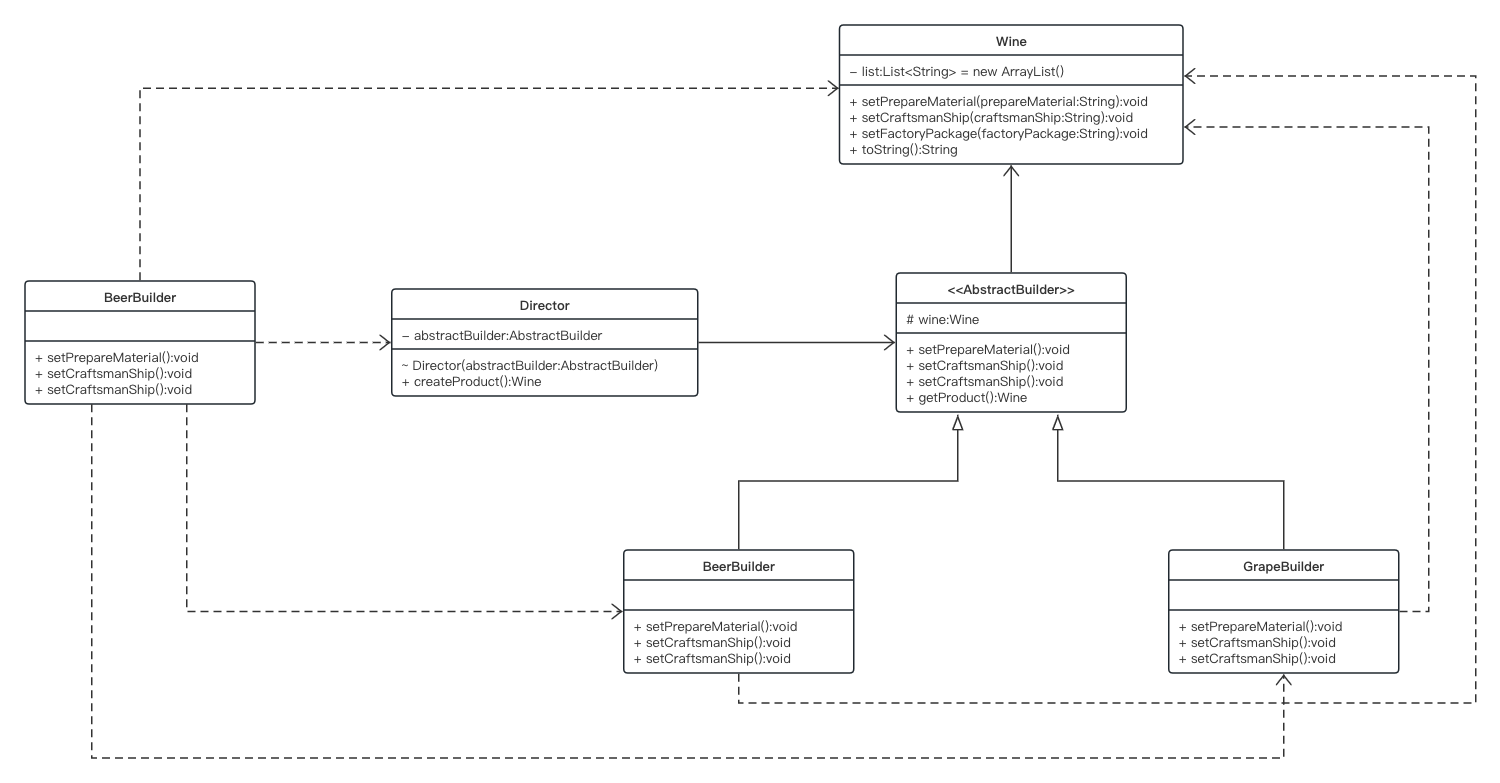
【设计模式-6】建造者模式的实现与框架中的应用
建造者模式又被成为生成器模式,是一种使用频率比较低,相对复杂的创建型模式,在很多源码框架中可以看到建造者的使用场景,稍后我们会在本文末尾展示几个框架的使用案例。 建造者模式所构造的对象通常是比较复杂而且庞大的&#x…...

PositiveSSL和Sectigo的多域名证书
首先,我们要知道PositiveSSL是Sectigo旗下的子品牌,提供多种类型的SSL数字证书,包括DV基础型的多域名SSL证书。Sectigo的SSL证书产品同样比较丰富,不仅有DV基础型多域名SSL证书,还有OV企业型以及EV增强型的多域名SSL证…...

Docker:docker exec命令简介
介绍 docker exec [OPTIONS] 容器名称 COMMAND [ARG...] OPTIONS说明: -d,以后台方式执行命令; -e,设置环境变量 -i,交互模式 -t,设置TTY -u,用户名或UID,例如myuser:myu…...
【大数据进阶第三阶段之Hive学习笔记】Hive的数据类型与数据操作
目录 1、Hive数据类型 1.1、基本数据类型 1.2、集合数据类型 1.3、类型转化 2、DDL数据定义 2.1、创建数据库 2.2、查询数据库 2.3删除数据库 2.4、创建表 2.4.1、内部表 2.4.2、外部表 2.4.3管理表与外部表的互相转换 2.5、分区表(partitionÿ…...
GPT2:Language Models are Unsupervised Multitask Learners
目录 一、背景与动机 二、卖点与创新 三、几个问题 四、具体是如何做的 1、更多、优质的数据,更大的模型 2、大数据量,大模型使得zero-shot成为可能 3、使用prompt做下游任务 五、一些资料 一、背景与动机 基于 Transformer 解码器的 GPT-1 证明…...
微创新与稳定性的权衡
之前做过一个项目,业务最高峰CPU使用率也才50%,是一个IO密集型的应用。里面涉及一些业务编排,所以为了提高CPU使用率,我有两个方案:一个是简单的梳理将任务可并行的采用并行流、额外线程池等方式做并行;另外…...
对回调函数的各种讲解说明
有没有跟我师弟一样的童靴~,学习和使用ROS节点时,对其中的callback函数一直摸不着头脑的,以下这么多回调函数的讲解,挨个看,你总会懂的O.o 回调函数怎么调用,如何定义回调函数: 回调函数怎么调用,如何定义…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...
